基于不规则断面的流量关系曲线率定分析

胡玉海

甘肃省疏勒河流域水资源局，甘肃 玉门 735211

一、基本情况

《敦煌规划》把党河流域作为核心区，包括敦煌市、肃北蒙古族自治县和阿克塞哈萨克族自治县，把疏勒河中下游的昌马、双塔灌区，涉及玉门市和瓜州县作为关联区，重点研究疏勒河干流灌区节水及可下泄生态水量。《敦煌规划》确定了完成目标，到2015年，双塔水库下泄生态水量7 800万m3，到达瓜州～敦煌边界双墩子断面水量2 700万m3；到2020年，双塔水库下泄生态水量不低于7 800万m3，到达瓜州敦煌边界双墩子断面水量不低于3 500万m3，进入西湖玉门关断面水量不低于2 200万m3。柳敦断面作为疏勒河下游监测生态下泄流量的关键性断面，对生态流量有效监测有着非常重要的作用，由于柳敦公路的施工，造成原有水位流量监测断面不能正常使用。为了能够精准计量下泄生态流量，分析流域水资源生态效益，科学评价《敦煌规划》实施成效，对现有不规则河道水位流量关系进行率定，为下泄生态水量计量提供水利技术支撑。

二、计算方法

目前流量测流的方式分为以下几种，有缆道测流、水工建筑物测流、水位比降法推算流量和雷达水表面波流速测量再推算流量。这几种测流方式都适于特定的水利条件和水流环境。缆道测流是我国早期使用的一种测流方式，目前来说，技术相对较为完善，特别是全自动缆道测流系统测流精度可达到95%～98%，缆道测流常见于不规则断面的流量测量，但对于小型的不规则河道和野外管理的不适宜，从经济角度考虑多采用其他测流方式。超声波时差法和水工建筑物等测流方式都适用于断面较稳定，形状较规则的。目前，监测断面尚未修建规则断面，仍然为不规则的天然河道断面，直接绘制水位-流量关系曲线比较困难，本次引入栅格法，选定断面的形状，以在选定断面上插入方格的数量推求不同水深的过流面积，通过水准测量及试验等方法率定计算参数，计算确定水深–流量的关系曲线。在实际计算时，所用的基本公式为曼宁平均流速公式和流量计算公式：

式中，v为水流速度，（m·s-1)，n为曼宁系数（s.m-1/3），R为水力半径，（m），I为水力坡降，计算时以河道坡度近似代替，Q为流量，（m3·s-1），A为过流面积，（m2），h为水深，（m）。

（一）监测断面横断面绘制

通过现场勘测，河道最大水深1.1m,河道宽度16m。对于任意断面，过流面积是水深的函数，由于过流断面为不规则断面，面积随水深变化规律不能直接确定。为了确定过流面积与水深关系，本文根据不同水深条件下在断面上插入的栅格数量，来推求不同水深时的过流面积。方格尺寸越小，同一水深下，断面上插入的方格数越多，用方格数量换算的面积越接近于该水深对应的过流面积。

方格尺寸根据水深和河道宽度来确定，为使过流面积更加精确，选取方格宽度方向0.2m、竖直方向（水深）0.1m（尺寸：0.1m×0.2m，面积：0.02m2)，在河宽为16m时，其对应的最大水深为1.1m，则在该断面上插入方格数量为671个，对应的断面面积为13.42m2。根据图1所示，选取不同的水深，推求出其对应的过流面积，最终求解水深–流量（h-Q）曲线。

（二）坡度与水力半径

过水断面面积与水力半径可以根据不同水深所包含的方格面积来确定，河川纵向坡度一般来说由专门的设备进行测量确定（水准仪），目前，按照实际测量的数值为0.002。水力半径根据不同水深的湿周和过水断面面积进行推算。

（三）糙率（曼宁粗度系数）

曼宁粗度系数（糙率n）是综合反映渠道断面粗糙情况对水流影响的一个系数，根据河道固体粒径的实际情况，参照水力学天然河道糙率表确定。结合河道河川特性实际，取河道糙率n=0.04。

表1 河道糙率参考表

三、流量关系曲线确定

（一）流量计算

将相关参数代入公式：

计算出不同水深下的流量，计算过程见表2所示。

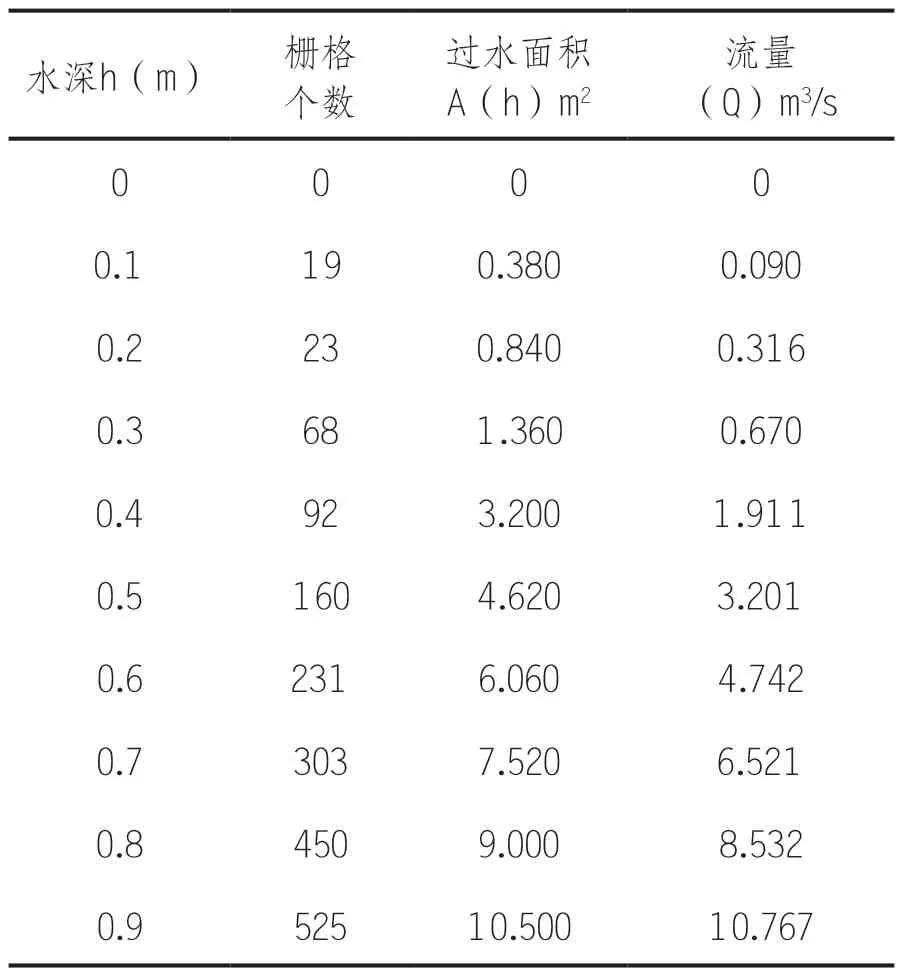
表2 水深流量关系计算表

图1 过流断面栅格示意图

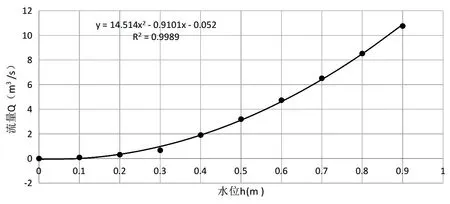
图2 水位-流量关系曲线图

通过计算，得出水深与流量的关系，绘制离散点图，添加趋势线进行曲线拟合。由图2所示，曲线与离散点拟合度较高（R2= 0.9989），说明曲线方程能够表示该断面不同水深条件下水位流量关系曲线，最后，拟合曲线对应的流量公式即为断面流量关系。

Q=14.514h2-0.9101h-0.052（R2=0.9989）

（二）曲线准确性检验

关系曲线的精准程度决定了数据的准确与否，为了验证和进一步率定曲线，要对关系曲线进行准确性检验，利用相对误差和绝对误差进行偏差分析。分析以实际观测值为基准，从绝对差值（ΔV）和相对误差（δV）对比计算值和实际观测值的差异，分析计算值的偏差情况，ΔV和δV的计算公式分别为：

其中，ΔV为绝对差值，δV为相对误差，当|δV|≤30%时认为两者的差值正常，否则为异常。

通过数据检验，不同水深条件下曲线计算的数值和观测值，都在30%正常范围内，除0.1m和0.3m,相对误差δV分别是0.976和0.464偏差较大以外，其他水深观测的数值和曲线公式计算的数值都非常接近，说明拟合曲线对应的流量公式可以准确反映断面过水水量，能够为观测流量提供技术支撑（计算见下表3）。

表3 水深流量关系计算表

综上所述，通过方格个数和面积求得的过水断面水深与流量关系曲线，曲线与离散点拟合度较高（R2=0.9989），曲线方程能够表示该断面不同水深条件下水位流量关系曲线，准确性检验后，不同水深条件下曲线计算的数值和观测值，都在30%正常范围内，除0.1m和0.3m，相对误差δV分别是0.976和0.464偏差较大以外，其他水深观测的数值和曲线公式计算的数值都非常接近，能够精准计量下泄生态流量，后期将进一步结合观测数据率定流量关系曲线，为下泄生态水量计量提供水利技术支撑。