基于目标驱动优化的海洋浮标平台系泊方案设计∗

（海军航空大学航空基础学院 烟台 264000）

1 引言

为了保证海洋浮标平台设备的可靠性和数据测量准确性，海洋浮标平台在海上漂浮需要一个稳定的状态，如何在保持安全可靠的情况下兼顾经济性，是当前浮标系泊需要解决的问题，系泊系统的设计具有非常重要的意义。目前，常见的方法都是根据遗传算法或神经网络方法来计算布线位置。主要通过优化锚泊线的布置方式来最大限度地减小系泊状态下锚链的平动位移量［1］。以锚链抛锚距离和方位角作为变量，通过正交试验选取了最优的系泊布置方案［2～3］。这些研究主要是针对船舶系泊缆索位置的优化，本文以缆索的物理性质的优化为研究的重点，对具有对称的特点浮标平台进行系泊方案设计与优化。

2 缆索优化设计

通过采用有限元分析对缆索截面参数以及长度来进行优化设计［4～6］，分析的过程中插入了程序语言对不同缆索参数的选用进行了自动化处理，从而进行批量的水动力计算和后处理。在该段处理中，将待选的各种截面参数化，程序可以直接调用对应截面参数进行计算。

2.1 实验变量设计

对缆索优化的目的是尽可能减小缆索总重量，且保证浮台的摇荡幅值和缆索张力峰值也尽可能小［7～8］。优化分析的输入变量有缆索总长度、单位长度缆索重量、轴向刚度以及等效直径［1］。缆索轴向刚度和等效直径是与单位长度缆索重量紧密相关的，即相同的材料，缆索越粗其重量与刚度就越大。根据缆索截面积与其重量与刚度的正比例关系，可在缆索重量、轴向刚度和等效直径三者中选择缆索重量作为设计变量，另外两个变量作为其表达式关系。那么实际的输入变量就是缆索总长度与缆索重量两个不相关的变量。现有的方案下，缆索的总长为55m，缆索重量为150kg/m。鉴于缆索的总长较短，如继续减短，则有可能增大浮台的初始拉力，因此缆索的总长取更大的值，而缆索的重量为经济性考虑则取更小的值，各输入变量的设计区间见表1。

表1 各输入变量的设计区间

输出变量指定为浮台垂荡运动的谷值与峰值，浮台摇动角度的谷值与峰值以及缆索张力的峰值。

2.2 实验设计

表2 实验设计中的输入变量与输出变量

本文通过设计实验［9］建立响应面模型。因为实际的设计变量只有两个变量：缆索重量与缆索长度，那么在实验设计中可将缆索重量变化8次，缆索长度变化6次，来进行参数化计算。缆索重量值分别为150、135、120、105、90、75、60、45，量纲kg/m；缆索长度分别为55、56、57、58、59、60，量纲为m；一共进行6×8=48次计算，由于篇幅所限表格中只列出部分计算结果。

2.3 响应面分析

实验设计的48次离散样本采用ANSYS的响应面程序［10～11］，对离散的样本进行连续插值计算，生成了1000组数据，随后将各个数据生成三维坐标系的统计图，形成了响应面，通过对响应面的分析便能够得到各参数之间的关系。通过分析响应面［12］，以此达到优化的目的。

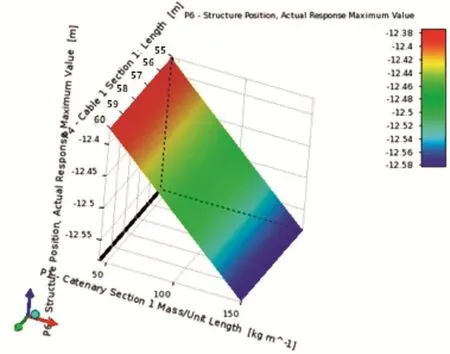
图1 浮台垂荡幅值的三维响应面

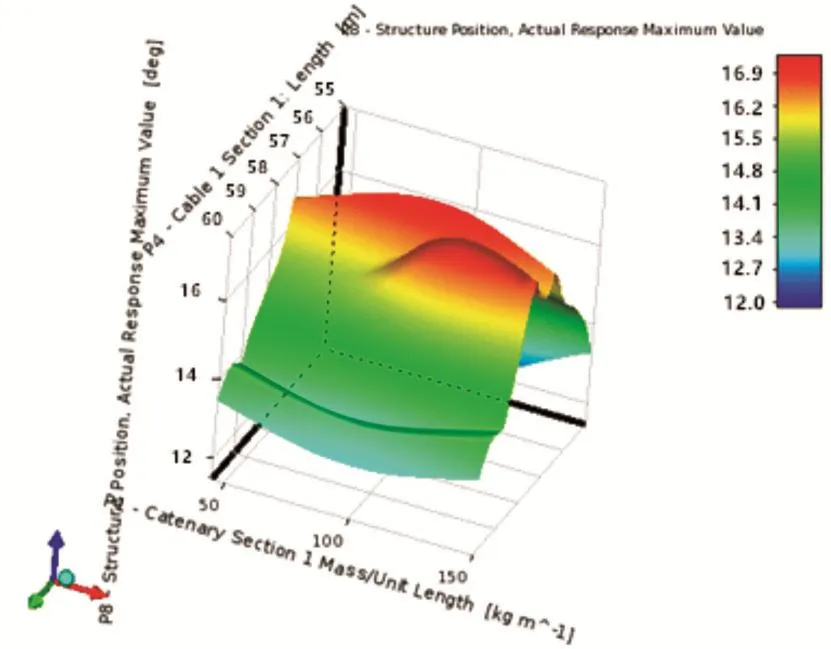
图2 浮台摇动幅值的三维响应面

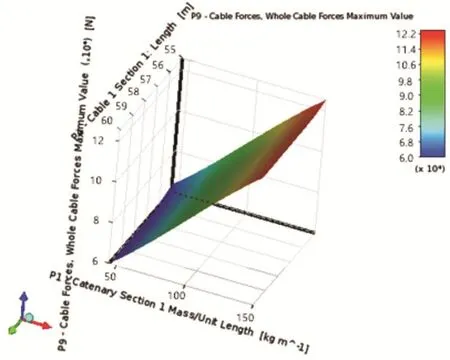
图3 缆索张力峰值的三维响应面

其中：X轴为单位长度缆索质量；Y轴为缆索长度；Z轴分别为浮台的垂荡幅值、浮台的摇动幅值和缆索的张力峰值。由图1可得，浮台的垂荡振幅与绳索的长度无关，而与绳索的质量有关，质量越小垂荡振幅越小。

由图2可得，浮台的摇动幅值与绳索的质量关系较小，而与绳索的长度关系较大，绳索较大或较小时摇动幅值较小。

由图3可得，缆索张力峰值与缆绳的长度关系较小，与绳索的重量关系较大，绳索的重量越大，缆绳的张力峰值越大。

从变量的敏感度来看，浮台的垂荡运动和缆索的张力与缆索的重量相关性较大；而浮台的摇动角度与缆索长度相关性较大。

2.4 目标驱动优化

指定各变量的优化目标见表3。

表3 输出变量与优化目标

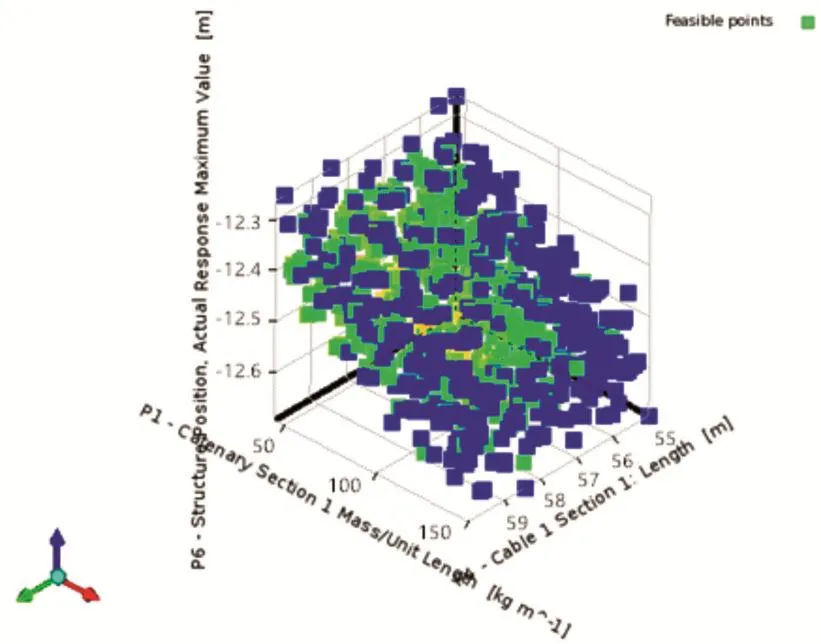
图4 浮台垂荡幅值的可行样本分布图

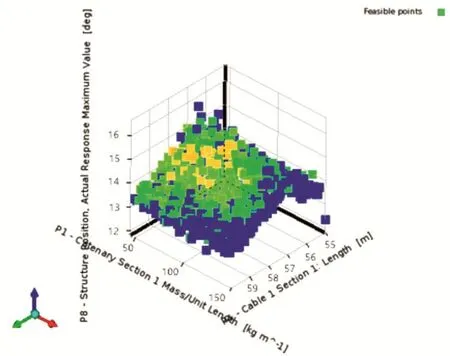
图5 浮台摇动幅值的可行样本分布图

通过仿真实验在响应面得到的大量连续样本中进行筛选，图4～图6分别显示浮台的垂荡运动幅值、浮台的摇动角度幅值和缆索的张力峰值在满足优化目标条件下的可行样本分布图。系统根据垂荡幅值、摇动角度幅值以及缆索张力峰值的优化目标对这些可行的样本进行最优解的筛选。

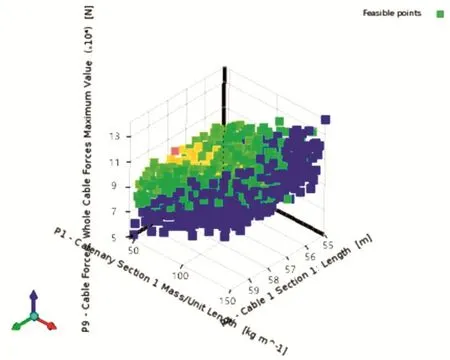
图6 缆索张力峰值的可行样本分布图

根据自动筛选得到的最优样本见表4。从结果可以看出，通过优化可以减轻缆索18%的重量。

表4 初始方案与最优方案的变量对比

3 五级海况下最优样本的核算

以表4中的缆索重量和缆索长度反馈给AQWA软件，进行水动力时域分析。核算了在五级海况海况两种海洋环境下的结果。图7和图8分别为X、Y、Z、Rx、Ry、Rz方向浮台自由度的时间历程曲线。

相比初始设计的缆索总重量8250kg，此时的缆索总重量为6768.65kg，减重18.0%。相比初始设计的缆索张力峰值122.12KN，此时的缆索峰值为104.80KN，降低14.2%。如表5所示。

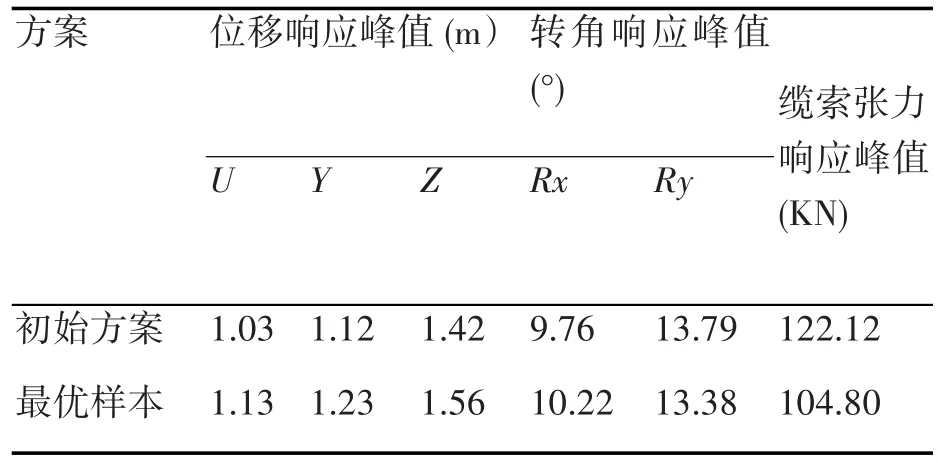
表5 五级海况下初始方案与最优样本的结果对比

图7 浮台X、Y、Z自由度时间历程曲线

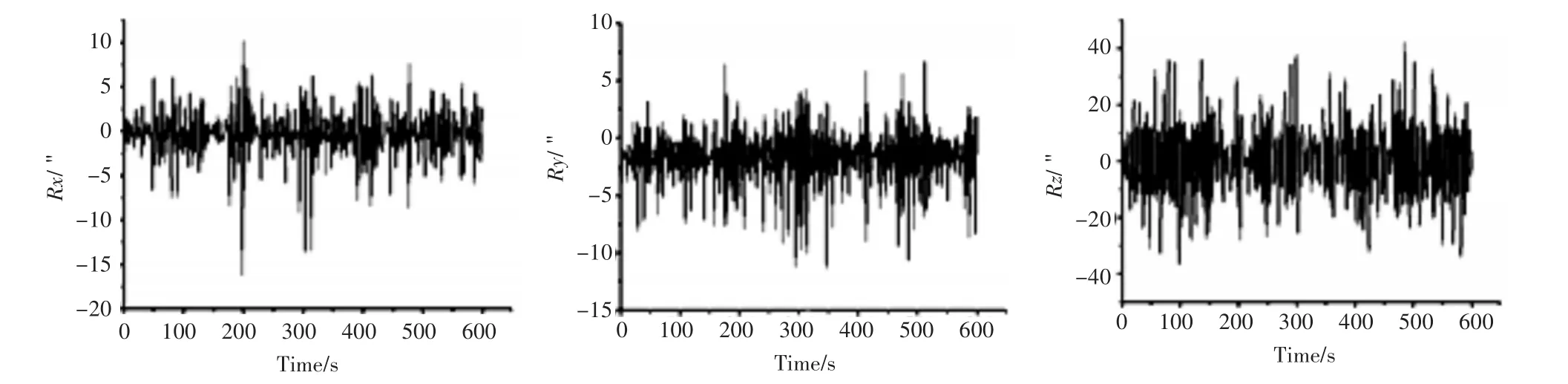
图8 浮台Rx、Ry、Rz自由度时间历程曲线

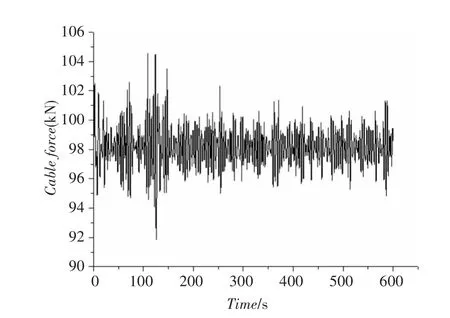
图9 缆索的张力时间历程曲线

4 结语

采用AQWA水动力分析结合ANSYS Design Exploration优化分析模块对海洋通信浮台的系泊系统进行优化分析。得到如下结论：

1）通过目标驱动的优化设计，得到了最优的缆索重量和缆索长度，缆索共减重18.0%。

2）经过对最优设计参数分别在五级海况和百年一遇海况下的核算，得到浮台的垂荡运动和摇动运动幅值在优化前后变化较小，在五级海况下缆索张力峰值降低了14.2%，在百年一遇海况下缆索张力峰值降低了5.3%。

仿真计算结果证明提出的优化方案和设计，能够为缆索在满足的强度要求下充分考虑轻量化设计，使系泊方案具有良好的经济性，为海洋浮标平台的系泊制造设计提供了一定的解决方案。