飞翼布局无人机数学建模及容错控制∗

林建欣 陈 洁，2

（1.海军航空大学岸防兵学院 烟台 264001）（2.海军航空大学战勤学院 烟台 264001）

1 引言

在无人机研究领域，飞翼布局无疑是极为经典的一种布局模式。具有结构简单、高机动性、隐身性、翼身融合设计等诸多优点。但是由于飞翼无人机所执行的任务通常具有范围大、续航要求高、环境条件恶劣的特点，因此有关其控制系统的可靠性要求就颇为严格，这就需要它具有一定的容错控制能力，确保无人机能够顺利地执行任务并安全回归本地。

从外形上看，飞翼布局没有垂直尾翼，但可以通过矢量推力装置，以及数量较多的操纵舵面，来实现飞机的稳定飞行。

操纵面作为无人机的执行机构，长期频繁地执行任务，是系统中最易发生故障的部件之一，解决飞翼无人机的操纵面故障问题是必须要解决的难题。

本次研究的飞翼无人机基本构型可以参见图1，该无人机具有4对操作舵面：升降副翼融合了副翼与升降舵的功能，主要控制无人机的俯仰通道。余度舵与副翼相接，可以按照实际需求对冗余舵的控制作用进行调整，也可充当副翼并发挥升降舵的功能。副翼主要针对滚转通道进行控制。该无人机的偏航运动则由最外侧的开裂式阻力方向舵的开合作用来实现。该型号无人机的具体性能参数见表1。

图1 飞翼无人机布局

表1 飞翼无人机性能参数

2 飞翼无人机数学建模

2.1 动力学方程组

根据牛顿第二定律，可以推导出无人机在重力、空气动力和推力合成的综合作用外力FΣ以及力矩MΣ作用下的非线性动力学方程组以及角动力方程组。其中动力学方程组是速度V在机体坐标系的分量u，v，w的导数与合外力FΣ在机体坐标系上的分量Fx，Fy，Fz之间的关系：

式中：

角动力学方程组是角速度Ω在机体坐标系上的分量p，q，r的导数与MΣ的分量M，L，N之间的关系：

其中：

2.2 运动学方程组

借助机体与地面坐标系之间相对位置关系就能推导出运动学方程。无人机的运动相对于地面姿态的动态变化规律就能借助于角运动方程来进行描述。

按照上述两个坐标系的转换关系可知，机体相较于地面坐标系的转动角速率和对应的转动角速度Ω在前者坐标系中分量p，q，r，存在着下面关系：

V与u，v，w的关系为

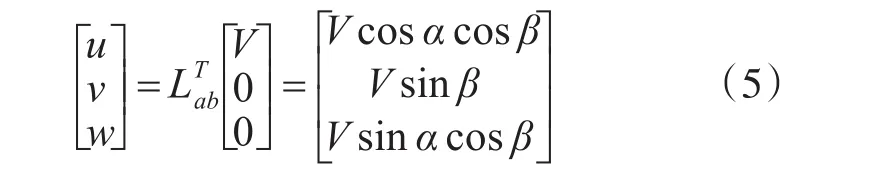
因此有

以上建模过程可得到关于飞翼无人机模型12个非线性微分方程，同时状态量与控制输入向量之间也有着相应的非线性函数关联性，输入向量为

3 飞翼无人机自适应容错控制

3.1 自适应控制技术

自适应技术是20世纪50年代在自动飞行控制中开发的应用技术，用于应对许多未知参数和干扰的飞行控制。

当周围环境变化很大时，自适应控制基于操作系统的参数与期望系统的参数之间的差异做出新的决定，并适当调整相应的控制参数与结构，使得受控对象仍然能够接近期望的指标。

1）模型参考自适应控制

这种控制系统所选用的参考模型是以预期性能设计为基础的动态系统，可以借助于参数的自动反馈调整使得该系统能够与参考系统进行逼近。

在文献［1］将此系统与信号综合自适应算法进行融合，成功开发出有着较高鲁棒结构的容错控制系统，解决了未知干扰和系统故障，使系统仍然按照预期的性能运行指数。文献［2］采用反步法设计状态反馈自适应容错控制器，其中广义误差状态向量作为唯一的自适应律变量因子。文献［3］将自适应状态反馈和输出跟踪方法相结合，设计了一个容错控制器，解决了执行器的卡住故障，实现了良好的容错控制效果。

2）自校正自适应控制

自校正自适应系统主要特点是通过控制输入和输出识别系统参数，并通过识别结果调整控制参数，以达到系统性能指标。文献［4］在研究中借助于自适应状态观测装置来对系统的动态进行检测，然后借助于反馈管控输入与故障估计完成该容错系统的开发。在文献［5］中则借助于自适应卡尔曼滤波装置获取相应的信息来进行检验，由此准确判断故障，最后利用自适应管控方法实现控制装置的重构。在文献［6］之中，将状态估计值当成状态反馈输入至，并利用该卡尔曼滤波装置来对状态残差进行估量，并调整线上的控制律以获得稳态调节器。

3.2 自适应容错控制器设计

对飞翼无人机的自适应容错控制系统进行如下设计。

舵面故障描述满足线性定常系统［7～9］：

其中舵面故障通常包含以下情况：舵面的浮动、损伤与卡死。

无人机舵面故障仅仅存在上述的单个舵面故障，也可能是多个舵面故障的组合。表示舵面故障的无人机状态方程可以具体表示为

其中，G为舵面故障分配矩阵，fa(t)为舵面故障的函数，对于不同的故障，fa(t)具有不同的函数形式。

当飞翼飞机舵面出现以上故障时，其他舵面通过控制系统重新操作以实现补偿故障舵面的效用，从而使飞机继续稳定的飞行。

考虑当系统只存在舵面故障的情况，此时容错控制系统的结构控制器如下：

上式中，Γi是正常数，有边界，bi是B的第i列。

自适应控制增益方程K2(t)如下：

在上式中正常数依次为α和γ，而P则为正定矩阵。

(t)通过以下自适应律调节：

r是任意常数。

根据式（9）、（10），闭环容错控制系统模型可以写成：

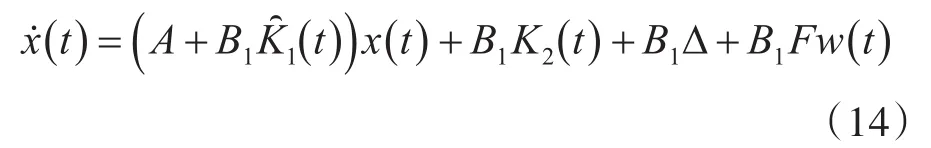
令

由于K1，i和k3为未知常数，因此可以得到如下误差系统：

定义式（15）、（16）分别为闭环系统与误差系统，对于满足式（10）、（11）、（12）的自适应闭环系统，假定存在正定对称矩阵P，并选择式（12）作为控制增益方程，式（11）、（13）作为自适应律，则所得容错系统是渐进稳定的。

通过以上设计过程，完成了对飞翼无人机自适应容错控制系统的设计，将在第4节对设计好的控制系统进行Matlab/Simulink仿真，分析控制性能。

4 容错控制仿真建模与分析

4.1 Matlab/Simulink仿真建模

本节主要针对飞翼无人机横侧向运动，利用Matlab软件搭建控制模型，相关参数选择如下。

飞翼无人机的横侧向运动，参照第2节建模以及系统描述（8）可以得到表示。

表达式中，各状态量以及相关系数矩阵表示为

其中，β为侧滑角，p为滚转角速度，r为偏航角速度，φ为滚转角，δa为副翼偏转角，δr方向舵偏转角。飞翼无人机在飞行高度15000m，飞行速度为0.6Ma 的典型状态飞行［10］。

系统方程（8）中，系数矩阵等取值如下：

根据文献［11］，方向舵的舵偏角范围为［-60o，+60o］，副翼可用舵偏角为［-45o，+45o］；根据文献［12］，仿真时给定如下参数和初始值条件：

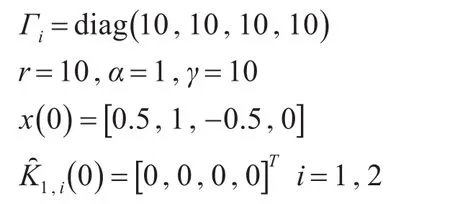
4.2 仿真结果分析

在本小节，对飞翼无人机有无容错控制调节的两种横侧向状态响应情况进行了对比，前后对比时基于同样的故障条件与初始参数选择，并分别对容错控制效果进行了仿真分析。

在1s时，现舵面故障，若αi=40°，该时间节点后的侧滑角与滚转角状态响应为

图2 侧滑角随时间变化

图3 滚转角随时间变化

如图可知，在故障条件下，无人机的侧滑与滚转角响应立刻出现变化，且不能达到稳定状态，此时，无人机不再具有保持稳定飞行的能力。

舵面故障状态下，加入容错控制律调节的无人机状态响应，同样在1s时发生舵面故障，其中αi=40°，1s后关于无人机侧滑角与滚转角的响应如下。

图4 容错系统作用下的侧滑角动态变化

图5 容错系统作用下的滚转角动态变化

针对仿真结果进行分析，若是舵面产生故障，在设计好的自适应容错控制律的作用下，可以对舵面加以补偿，从而保障无人机维持稳定飞行。

根据图4和图5可以看出，容错控制律不仅能实现输入指令的无静态误差响应，而且响应的过程没有超调量，调节时间也较短。

综上所述，本文提出并设计的容错控制律，具有良好的控制性能和较强的鲁棒性，能够满足飞翼无人机的横侧向飞行品质要求。此外，从仿真结果可以预测，该方法对于解决一类舵面故障的无人机飞行问题比较有效，具有推广与深入研究的价值。

5 结语

本文以飞翼布局无人机的运动方程以及舵面故障模型为基础成功设计了无人机自适应容错控制系统，并借助于软件对系统进行了仿真分析，对于未进行容错控制的故障响应以及具有自适应容错控制的故障条件下的响应进行了前后对比，验证了所设计的容错系统的可靠性以及有效性。

相对于带有故障检测和诊断要求的容错控制方法，本文设计的自适应容错控制器，免去了上述诊断环节，降低了系统对于故障诊断的依赖性，同时降低了诊断失误对系统带来的风险。

本文设计的自适应容错控制器，基本可以解决参数不确定性问题，舵面故障补偿控制问题。但是本文只体现了参数在线性定常系统下的常值变化，实际上，该方法是否可以拓展并运用到参数时变的系统问题中还有待进一步研究。