基于特征向量的点云配准方法研究

俞 浩, 高 飞

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

0 引 言

三维激光扫描技术是20世纪90年代中叶出现的新兴技术,它可以不接触被测物体得到被测物体表面大量的密度高的三维点信息以及反射率等信息,由于三维激光扫描的快速性、准确性,因此该技术又被称为“实景复制技术”。该技术被广泛运用在逆向工程、虚拟现实、古建筑保护与修复等领域。

通常在外业采集数据时,往往对某一物体不能通过一次扫描得到完整的三维点云数据,因此在实际作业时,需要从不同角度对物体进行数据采集,因为在不同角度下进行测量时坐标系不同,所以必须要通过一定的方法对将不同角度下的点云数据进行点云配准,即将不同坐标系下的点云数据转换到同一个坐标系之下,从而得到物体完整的三维点云数据。常见的粗配准方法有七参数转换法和四元数法。

七参数转换法就是要求得两点云所在坐标系之间的3个平移量、3个旋转量以及1个尺度变换参数。转换公式如下:

X=ΔX+(1+k)RP

(1)

R=R(α)R(β)R(γ)

(2)

(3)

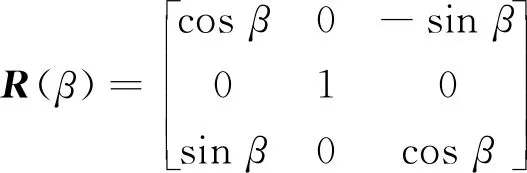
(4)

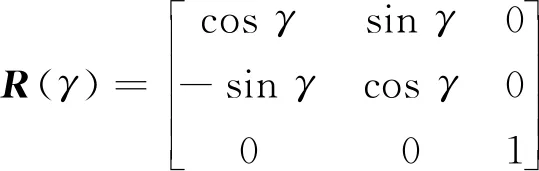
(5)

由(1)式、(5)式可得:

(6)

其中,X、Y、Z为目标点云坐标;Δx、Δy、Δz为3个平移参数;k为尺度变换参数;α、β、γ为3个旋转参数;px、py、pz为源点云坐标。

由(6)式可知，得到7个转换参数就可以实现源点云坐标到目标点云的转化。

四元数是Hamilton在1843年找到的一种扩展的复数,于1986年由Faugeras和Hebert用四元数进行配准研究[1]。一个四元数h拥有1个实部和3个虚部,即

h=q0+q1i+q2j+q3k

(7)

其中,i、j、k为四元数的3个虚部单位。四元数是一个包含4个矢量的阵列:

(8)

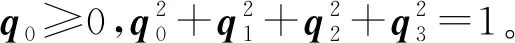
(9)

(10)

定义源点云与目标点云的质心为:

(11)

两点云之间的协方差矩阵为:

(12)

由协方差矩阵构成的4×4对称矩阵为:

(13)

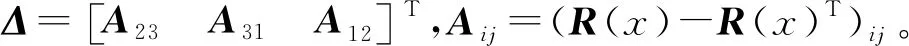
计算Q(R)的特征向量与特征值,其最大特征值对应的特征向量为qR=[q0q1q2q3]T。

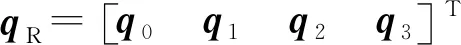
qT=μx-R(qR)μp

(14)

本文通过引入特征向量的欧氏距离来解决两片点云间的特征匹配问题,通过七参数转换法对点云坐标进行转换,确保在进行最近点迭代法前两点云有着比较好的初始位置。本文通过应用实例验证该方法的可行性。

1 特征点匹配

要实现不同坐标系下的点云配准,就要求解出不同坐标系之间的转换参数(旋转矩阵R和平移矩阵T),那么就必须要对不同坐标系下的相同点进行匹配。

目前特征点匹配主要分为2类:① 通过控制点来进行坐标系之间的转换[2];② 根据点云重叠部分的点以及点与点之间的固有关系来进行配准。这种配准方法主要有求解点与点之间的配准算法[3-4]、求解点与平面之间距离的配准算法、计算豪斯多夫距离来衡量点云相似度以及基于几何特征的配准算法[5-6]。著名的最近点迭代法就是通过求解点与点之间的欧式距离的最小值来进行点对匹配,文献[7]通过计算点邻域的切平面与点之间的距离来进行匹配,但是这种方法的鲁棒性不是太好。文献[8]进行了一些豪斯多夫距离在点云配准的理论研究,但未进行实际配准应用。

总的来说,第2种配准步骤主要分为寻找对应点和求解对应关系2步。

尺度不变特征变换(scale-invariant feature transform,SIFT)算法可以将不同坐标系下的点云里的特征点提取出来。SIFT算法是David Lowe在1999年提出,2004年整理完善的[9],最初是一种根据电脑视觉的算法来侦测与描述影像的局部特征点,这些局部特征点可以帮助识别物体。该算法同样可以运用到点云数据处理中来,其实质是计算出特征点的方向。它所找出来的关键点其实是一些在点云数据中比较突出的点,这些点不会因视角、光照等因素而改变。

在将特征点提取出来后,就可以用KDTree对这些特征点进行其法向量的求解。通过对其邻域点集求法向量来近似代替其法向量[10]。对邻域点的三维坐标进行中心化,求得协方差矩阵并对角化,求得3个特征值、最小特征值对应的特征向量即为法向量。

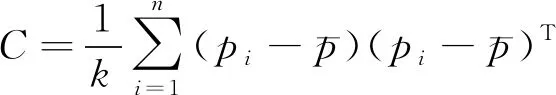
(15)

C·nj=λj·nj

(16)

通过对不同坐标系下的点云数据P的所有特征向量ni(i=1,2,3,…,n)和点云数据Q的特征向量nj(j=1,2,3,…,n)求解欧式距离,若最小欧式距离小于一个阈值ε,则这2个特征向量所对应的特征点即被认为是在不同坐标系下的相同点；若最小欧式距离大于这个阈值ε,则不进行匹配,进行下一个特征向量的最小欧式距离的求解。

运用求解欧式距离对2个不同坐标系下的特征点进行匹配的具体流程如图1所示。

图1 计算欧式距离匹配点对流程

2 点云粗配准

用匹配好的两组不同坐标系下的点云数据进行七参数求解[11]，即

A=(1+k)RB+T

(17)

加上最小二乘的约束条件,得出一个最符合的七参数。其中

(17)式中,A为目标点云;B为源点云;R为旋转矩阵;T为平移矩阵;k为缩放比例。由于点云坐标式基于扫描仪的极坐标系求出,因此缩放比例k可以忽略。

(17)式可以变为:

A=RB+T

(18)

结合最小二乘的约束条件：

VTPV=min

(19)

可以得到一个最为准确的旋转矩阵R和平移矩阵T。

3 点云精配准

运用粗配准求得的旋转矩阵R和平移矩阵T可以将源点云数据转换成目标点云附近,实现2片点云的粗配准。但是不同点云之间会有分叉的情况出现,基于这种情况,引入最近点迭代法对点云位置进行精配准。

最近点迭代法(ICP算法)最先由Besl和Mckay提出[12-13],其本质就是在最小二乘的约束条件下,求出2个点集之间的变换关系,假设{Pi,i=1,2,3,…,n}为源点集,{Qi,i=1,2,3,…,m}为目标点集,则构建函数为：

(20)

通过迭代确定这2个点集的最优匹配,直到达到设定的某个收敛准则为止,也就是通过不停地求解这2个点集的变换关系，并且根据这个变换更新2个点集的位置,直到变换关系满足这个收敛准则,这时2个点集之间的变换关系就认为是最优解，即旋转矩阵R与平移矩阵T最优,其具体步骤为:

(1) 首先从源点云及目标点云中分别提取点集Pi∈P,Qi∈Q。

(2) 计算源点集中的点与目标点集中的点的对应关系,使得‖Qi-Pi‖2=min。

(3) 计算旋转矩阵R与平移矩阵T,满足关系如下：

(21)

(4) 运用旋转矩阵R与平移矩阵T变换P点云的位置,即Pi′={Pi′=RPi+T}。

(5) 计算均方差δ,具体公式如下：

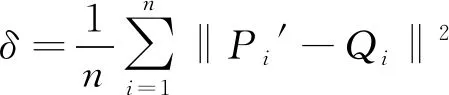
(22)

(6) 比较δ与最初设定的阈值ε。若δ<ε,则停止计算；若δ>ε,则重复步骤(2)～步骤(6)。

这样经过每一次迭代,Pi就会更靠近点云Qi,基于这种思想,Besl证明了这种方法的收敛性。

4 应用实例分析

实验数据为2个不同坐标系下的某古文物鼎的点云数据，初始点云如图2所示,左侧点云为源点云,右侧点云为目标点云,目的是要将左侧点云向右侧点云转化。先用SIFT算法提取出特征点后再对特征点进行法向量求解，并进行点对配对,得到的粗配准的旋转矩阵R和平移矩阵T分别为:

图2 两点云初始位置

粗配准的结果如图3所示。用最近点迭代法进行迭代50次实现精配准,再迭代的过程中每一次迭代都会生成一个旋转矩阵及平移矩阵,相对应的源点云也就一次一次地更加逼近目标点云。其中最后一次的旋转矩阵和平移矩阵分别为:

图3 粗配准后的点云位置

将初始点云直接进行ICP算法陷入的局部最优的情况如图4所示。

图4 直接运用ICP算法陷入的局部最优情况

直接进行ICP算法每一次迭代的具体误差值以及运行时间如图5所示,经过粗配准之后再运用ICP算法进行精配准后的效果如图6所示。

图6 经过ICP算法迭代后的两片点云

从图4可以看出,直接进行ICP算法进行点云配准会导致点云并不能很好地拼接在一起,甚至会出现局部最优的情况,如图5所示,虽然迭代后的误差值逐渐趋于收敛,但是实际位置并没有很好地配准。因此本文的粗配准算法有一定的必要性,通过粗配准将两点云调整至大致重叠的位置,它们之间仅仅相差较小的旋转和平移。

图5 直接ICP算法运行时间及误差值

从图6可以看出,经过粗配准之后再进行点云数据精配准,两片点云几乎完全重叠,迭代50次后均方误差达到0.000 111 194 m,在运行时间方面,文中程序所用的计算机配置为Intel(R)Core(TM)i5-7500处理器,16 GB内存,直接ICP算法花费时间为63 289 ms,经过粗配准之后再进行ICP算法的花费时间为48 011 ms。具体差异见表1所列。

表1 2种方法差异

5 结 论

由于多站数据的坐标系不同,初始点云的位置差异比较大,直接进行ICP算法无法准确配准拼接,甚至会陷入局部最优的问题。而仅仅用四元数法或七参数转换坐标进行粗配准并不能达到所要的精度。本文针对这个问题提出新的解决方法,即先利用特征点对应的特征向量寻找点对并求解七参数的方法进行粗配准,将点云位置之间的刚性变换变小,再通过ICP算法对点云数据进行精确配准。这样既可以解决直接进行ICP算法陷入的局部最优问题,也可以达到所需要的精度。