基于KLT多视图特征跟踪的物体三维重建

2020-08-05吴正斌彭业萍曹广忠曹树鹏

合肥工业大学学报（自然科学版） 2020年7期

吴正斌, 彭业萍, 曹广忠, 曹树鹏

(1.深圳大学机电与控制工程学院,广东深圳 518060; 2.深圳大学广东省电磁控制与智能机器人重点实验室,广东深圳 518060)

随着计算机视觉在诸多领域内被广泛应用,快速、准确获取目标物体所涵盖的三维信息成为目前视觉研究领域所关注的问题。三维重建是指通过相机获取目标物体的多幅图像,然后通过图像上的像素信息得到每幅图像间点的对应关系以及空间映射关系,再通过点和空间两者之间的关系得到目标物体的三维信息,最终完成对目标物体的三维重建。三维重建应用范围广泛,在医疗[1]、工业检测[2]、空间技术[3]等方面都有十分重要的应用。与双目[4]或者多目[5]立体视觉相比,单目立体视觉在成本、结构及获取图片的方式等方面有明显的优势,通过对多幅图像的处理可以完成对物体三维重建,达到多目立体视觉的效果。

目前,大多采用基于序列图像[6-11]的方法进行单目立体视觉的三维重建,此外,还有通过控制物体运动的方式进行三维重建[12]。文献[6]首先通过尺度不变特征转换(scale-invariant feature transform,SIFT)算法对特征点进行提取与匹配以获取空间点在两幅图像上的投影点,然后通过本质矩阵分解得到图像间的空间映射关系,再通过三角化初步获得双视图的三维点云重建,通过多视图位姿跟踪算法将已构造出的三维点与新增三维点进行三维点融合,最终通过曲面重建获取图像完整形貌。但使用SIFT进行角点提取与匹配的方法获取到的匹配点数量少。因此,本文采用Shi-Tomasi角点提取[13]和Kanade-Lucas-Tomasi(KLT)跟踪[14]的方法解决特征点匹配数量少的问题。文献[7]基于摄影深度求解算法的序列图像稀疏点三维重建算法,在求解3幅图像上的匹配点时,使用三焦点张量[15]计算3幅图像的匹配点,由于该方法求解3幅图像匹配点过于复杂,因此本文对此融合方法进行改进,通过KLT跟踪法对第2幅图像上的跟踪点继续跟踪,从而获得3幅图像上的匹配点,通过这些匹配点可以获得图像间的比例系数,通过比例变换以及坐标变换,最终完成目标物体三维重建。

1 多视图三维重建算法

通过相机可以获取物体的多幅图像,每幅图像上含有物体的大量信息,这些信息是以图像点的形式存在,这些图像点是物体在每幅图像的投影点。本文首先通过张正友标定法[16]获取相机内参,并对图像校正,减少投影点因相机畸变而造成的误差,通过Shi-Tomasi角点提取的方式得到第1幅图像的特征点,然后使用KLT跟踪器对这些特征点在第2幅图像上进行跟踪,从而得到在第2幅图像上的跟踪点,由第1幅特征点与第2幅上的跟踪点组成的点对就是匹配点对,将其扩展到整个图像序列上,就可以获得整个图像序列上任意相邻2帧图像的匹配点对,再对第2幅图像上的跟踪点进行KLT跟踪,得到在第3幅图像上的跟踪点,由第1幅图像上的匹配点与第2幅图像以及第3幅图像上的跟踪点组成的点对就是空间点在3幅图像上的投影点。

需要注意的是,任意相邻图像都需要经过2步获取匹配点:第1步,通过Shi-Tomasi角点提取+KLT跟踪获取匹配点;第2步,通过上幅图像的跟踪点+KLT跟踪获取匹配点。第1步是为了提供新的匹配点获取新的三维点云,第2步是为了得到同一点在3幅图像上的投影。

通过相邻图像上的投影点计算三维点云,由于是同一点,在经过坐标变换后,就会相差一个比例变换,最终需求解出比例变换系数。但在跟踪的过程中不可避免地引入一些误匹配的点,需要通过随机抽样一致(Random Sample Consensus,RANSAC)算法[17]来消除这些误匹配的点,最终得到每幅图像间点的对应关系。通过点的对应关系可以获得图像空间映射关系,通过三角测量获得物体深度信息,从而进行图像间的三维重建,并通过光束法平差(bundle adjustment,BA)算法[18]对重建结果优化。

本文通过透视n点(Perspective-n-Point,PnP)算法得到图像间三维重建模型的坐标变换参数,并通过3幅图像公共点之间关系获得比例变换参数,最终通过坐标变换与比例变换实现多幅图像融合。多视图三维重建流程图如图1所示。

图1 多视图三维重建流程图

1.1 Shi-Tomasi角点提取

三维重建需要获取空间点在不同图像的投影点对,但并非所有的投影点对都能够被方便地提取出来。只有那些与周围有明显差异的点,才能在2幅图像中被寻找到,并组成投影点对,这些有差异的点即特征点。图像特征点能反映出图像的本质特征,可用于标识图像中的目标物体,获取到的特征点数目越多,越容易重构出物体表面的轮廓。本文需要对多帧图像进行三维重构,因此需综合考虑单幅图片特征点提取算法的运行时间。目前关于特征点获取的方法有很多种,且有各自的优缺点,常用的算法有SIFT特征提取算法(简称“SIFT算法”)、Surf特征点提取算法(简称“Surf算法”)、Harris角点提取算法(简称“Harris算法”)、Fast角点检测算法(简称“Fast算法”)。本文综合考虑角点提取的数目以及单幅图像提取的时间,最终选取Shi-Tomasi角点提取算法(Harris算法的改进算法,简称“Shi-Tomasi算法”)作为获取特征点的算法,并在实验部分对这几种算法进行比较。

1.2 KLT跟踪

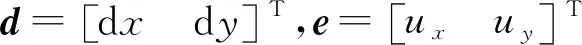
(1)

其中,I(e)、J(e)分别为图像I、J上的像素值;w(e)为窗口W的函数。为了ε取得最小值,将(1)式按照偏移量d的方向求偏导,使其偏导数为0,即

(2)

其中

将(2)式展开,其等式可以简化为:

Zd=f,

Z=∬WggTw(e)de，

f=∬W[J(e)-I(e)]gw(e)de。

解得偏移量d=Z-1f。

对得到的第2幅图像J的跟踪点通过上述方法继续跟踪,就获得空间点在第3幅图像上的跟踪点,从而获取空间点在3幅图像上的投影点。

1.3 获取图像空间映射关系

基本矩阵F是一个3×3的矩阵,表述了空间点与投影点对之间的关系。基本矩阵定义为:

x′TFx=0

(3)

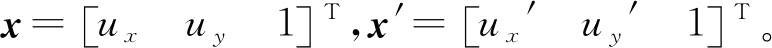
本质矩阵E是归一化图像坐标下F的特殊形式。本文采用的多幅图片是从同一个相机获得的,因此2幅图像相机内参相同,则E与F之间关系为:

E=KTFK

(4)

其中,K为相机内参。

将E进行奇异值分解(singular value decomposition,SVD)可得:

E=UΣVT=Udiag(1,1,0)VT

(5)

其中,U、V为单位正交阵;Σ为奇异值矩阵。由文献[19],可得空间映射关系有如下4种可能解:

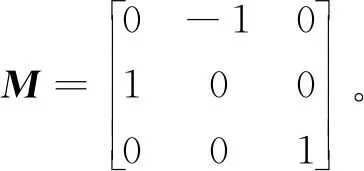
P1=[UMVT|u3],P2=[UMVT|-u3],

P3=[UMTVT|u3],P4=[UMTVT|-u3]

(6)

其中,u3为U的第3列向量;

这4种解中只有1种解是合理的,由E作标定重构4种可能的解,如图2所示。

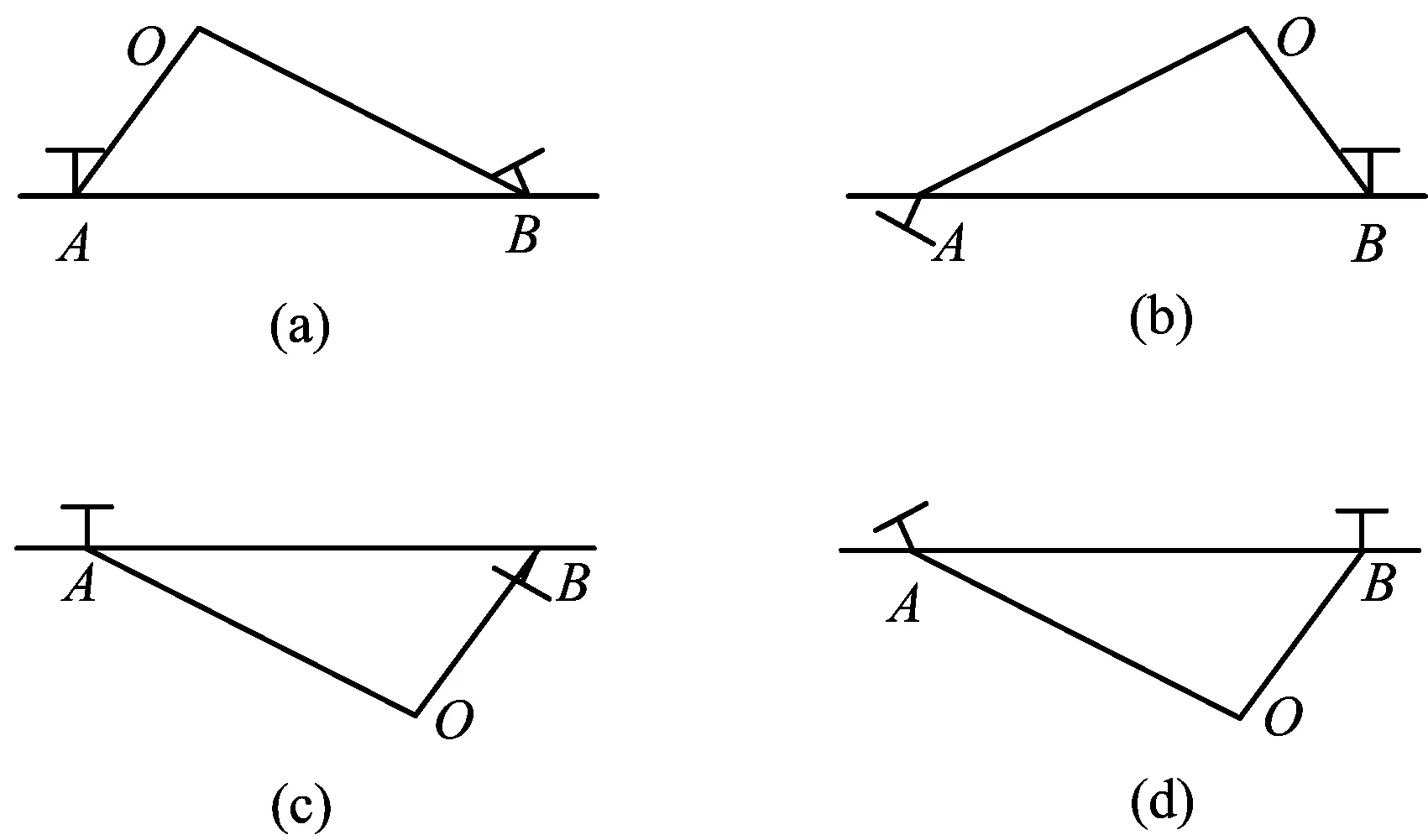
图2 由E作标定重构4种可能的解

4种解分别对应于图2中某一种情况,但具体对应关系未知。从图2可以看出,图2a满足重构出来的空间点在2幅图片前方这一条件,因此当空间映射关系处于图2a的情况下,空间映射关系的解为正确解。

1.4 三角测量

仅通过单幅图片无法获得像素的深度信息,需要通过三角测量的方式估计像素点的深度信息。

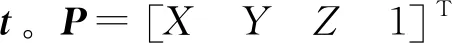
(7)

其中,λ1、λ2分别为投影点x、x′的深度。令

x1=K-1x,x2=K-1x′

(8)

其中,x1、x2分别为投影点x、x′在归一化平面的坐标。将(8)式代入(7)式,得到x1、x2的关系为:

λ1x1=λ2Rx2+t

(9)

将(9)式左、右两侧分别叉乘x1,得

λ1x1×x1=0=λ2x1×Rx2+x1×t

(10)

1.5 获取坐标关系和比例关系实现重建融合

图像序列上每2幅图像可以得到1组空间点,但由于空间点参考的世界坐标系不同,需要获得不同坐标系下空间坐标点的坐标关系。在计算平移向量t的过程中,在相差一个比例的意义下求解得到的结果,在获得物体三维空间坐标时也相应地相差一个尺度因子,因此,获得不同坐标系下重建三维点的坐标关系与比例关系显得尤为重要。

PnP算法通过求解3D点与2D点之间的关系求解相机坐标系与世界坐标系的关系,由于1.4节中空间点的坐标系与前一帧图像拍摄位置的相机坐标系重合,通过求解空间点与其在下一帧图像的投影点的关系,即可求得不同坐标系下重建三维点的坐标关系。高效透视n点(Efficient PnP,EPnP)[20]算法是PnP问题的一种求解方法,对于N个特征点,只要N>3就能够求解坐标变换Rreal和treal。

(11)

即可求解比例关系k。

(12)

其中,Rn、tn分别为第n帧融合点与第n+1帧图像之间的旋转矩阵与平移向量。

2 实验结果

本文通过机器视觉实验台获取物体旋转时的视频,从中选取图像序列进行实验。本次实验的机器视觉实验平台如图3所示,型号是XCY-SL-02。实验台由相机、光源及旋转台3部分组成,其中相机的型号为MV-CA020-20GC。

图3 机器视觉实验台

使用的软件平台为Matlab 2018a。相机的固定位置距离实验平台的高度为12 cm,而在实验时物体摆放的最高高度为2 cm,因此相机应倾斜摆放,使得物体在相机的中心。通过张正友标定法对相机内参与畸变参数进行标定,相机内参为:

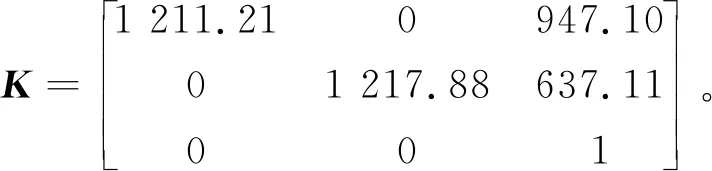
本文通过SIFT算法、Surf算法、Fast算法、Harris算法及Shi-Tomasi算法对图像进行特征点提取,通过手动调节阈值使得提取角点结果更佳。第1帧图像5种方法提取的效果图如图4所示。从图4可以看出,Fast算法和Harris算法相比于其他算法来说,角点分布不均匀。为了使得最终三维重建的形貌均匀,本文将不采用这2种算法。

图4 不同特征点提取方法效果图

5种算法的特征点数量、运行时间见表1所列。从表1可以看出,使用SIFT算法需要花费211 s,而其余算法不超过1 s。虽然Surf算法相比于Shi-Tomasi算法花费时间更少,而且满足角点均匀分布这一条件,但是Shi-Tomasi算法牺牲了一定时间获取更多角点,综合考虑特征点数目与运行时间2个方面,本文选取Shi-Tomasi算法进行角点检测。

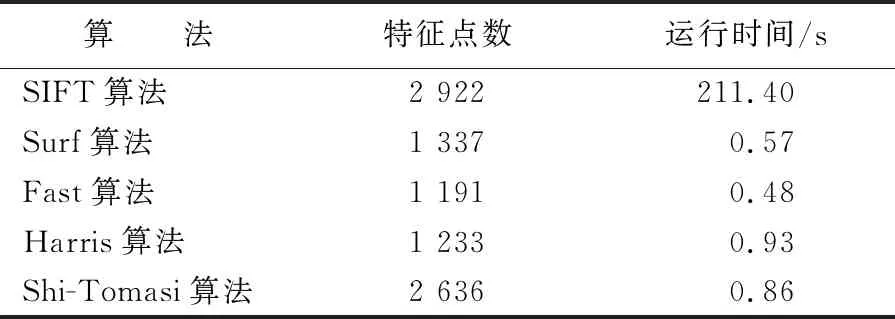
表1 5种算法特征点提取结果对比

获取2幅图像匹配点对有匹配与跟踪2种方法,现在大多数三维重建算法是在SIFT+匹配的基础上进行的,本文分别对第1帧与第2帧通过SIFT+匹配、SIFT+KLT跟踪、Shi-Tomasi+KLT跟踪3种方法获取匹配点。3种方法特征点匹配与跟踪结果对比见表2所列。由表2可知,传统的SIFT+匹配的方法获取匹配点数目少,而改进后的Shi-Tomasi+KLT跟踪的匹配点数目多,因此本文采取Shi-Tomasi+KLT跟踪方法获取匹配点,通过该改进方法能够有效增加匹配点数目。

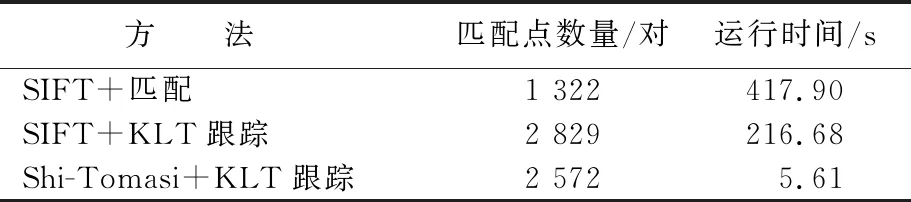
表2 3种方法特征点匹配与跟踪结果对比

对第1帧图像使用KLT跟踪得到2帧图像匹配效果图,如图5所示。这2帧图像上有2 572对特征点,通过x′TFx可以获取每个点重投影误差的平均值为0.014。从图5可以清晰看到物体的运动轨迹,这与真实的运动相符。将第2帧图像通过跟踪得到的2 572个特征点继续在第3帧图像上进行二次跟踪,得到3幅的公共点有2 491个。