攻角对高速射弹入水过程影响研究

梁景奇，王 瑞，徐保成，祁晓斌，李瑞杰

(西北机电工程研究所， 陕西 咸阳 712099)

超空泡动能弹由火炮发射，依靠动能对水下目标进行打击[1]。射弹入水过程是空中弹道转入水下弹道的过渡环节，弹体在极短的时间内穿越气水两种物性不同的介质，流场变化复杂，弹体会因入水砰击受到极大的冲击载荷，因此入水弹道在空泡形态、流体动力特性方面均与水下弹道存在较大的差异[2-4]。

针对高速入水问题，国内外学者作了广泛研究，Lundstrom等[5]以穿甲弹为对象开展了高速入水实验，给出了空泡半径预测公式；Park M S等[6]基于势流理论，采用切片法分析了高速入水冲击载荷；张伟等[7]进行了速度在35～160 m/s的平头、卵形和截卵形弹体入水实验，比较分析了弹体头部形状对入水弹道稳定性的影响；马庆鹏等[8]采用数值方法对锥头圆柱体垂直高速入水问题开展了研究,分析了航行体入水后速度及入水空泡形态变化；李佳川等[9]建立了射弹纵向运动的动力学模型，对弹体以不同扰动角速度入水过程进行了弹道仿真；卢炳举等[10]采用k-ω湍流模型模拟了高速射弹跨介质入水过程，分析了阻力与速度变化规律。攻角是入水弹道的关键影响因素，在探究攻角对入水过程的影响方面，施红辉等[11]利用高速相机观察了射弹大攻角冲击水面及出水流场，分析了相关物理参数；朱珠等[12]建立了大攻角入水弹道动力学模型，分析了入水攻角对弹道的影响规律。纵观研究现状，在传统理论建模还难以对高速跨介质问题进行准确预测的情况下，数值仿真仍旧是高速入水问题研究的有效途径，入水弹道的终点即为水下弹道的起点，射弹在入水过程由初始攻角引起的姿态变化将直接影响水下弹道，进而影响最终打击效能，因此有必要进一步探究攻角对入水过程的影响规律。

本文依托商用CFD软件FLUENT18.2及二次开发技术，结合动网格移动计算域方法，考虑流体压缩性，建立了高速射弹刚体运动与空泡流场相耦合的数值模型，以攻角为变量，研究了纵平面条件下射弹高亚音速垂直入水动态过程，探究了变攻角条件下弹体的升阻力特性、空泡形态及弹道参数的变化规律。

1 数值计算模型

1.1 控制方程

本文采用VOF多相流模型模拟相界面运动。VOF是一种在固定Euler网格下的界面捕捉法，常用于由两种及以上不相混液体组成的流体中，适用于多相间有清晰界面的流动。

1) 连续性方程

(1)

(2)

(3)

式中：ρ是流体混合密度；u是混合速度；n是相数，由于考虑了不凝气体，在这里，n=3；αk、ρk和uk分别为第k相的体积分数、密度和速度。

2) 动量方程

(4)

(5)

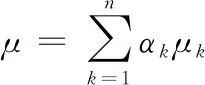
(6)

式中：p为压力；S为源项；τij为剪切应力；μ为混合动力粘度；μk为第k相的动力学粘度。

1.2 湍流模型

Realizablek-ε湍流模型主要针对充分发展的湍流，稳定性好，近壁面区域的流动状态使用壁面函数预测，对边界层网格要求较为宽松；结合尺度化壁面函数，其在不增加计算量和保持模型稳定性的前提下增加了模型的适用范围，模拟效果好。

湍流强度k方程：

(7)

湍流耗散率ε的方程：

(8)

式中：μt为湍动粘度；μ是流体的时均速度；σk、σε分别为k、ε方程的湍流能量普朗特数；C1、C2为经验常数；E为时均应变率；ν为运动粘度；xi、xj为x、j方向的距离。

1.3 空化模型

目前CFD计算中广泛采用基于输运方程的空化模型，这类模型以质量源项表示蒸发和冷凝过程，模拟水和水蒸汽之间的质量转换关系，该方法可较好地模拟空泡的非定常特性。

本文采用Singhal空化模型模拟高速射弹入水过程的空化绕流。Singhal空化模型由学者Singhal等人于2001年提出，该模型是一种“全空化”模型，基于Rayleigh-Plesset空泡动力学方程(R-P方程)，考虑了相变、空泡流体动力、湍流压力波动和非凝相气体等几乎所有的一阶影响。Singhal空化模型对于相间的质量传递可描述为：

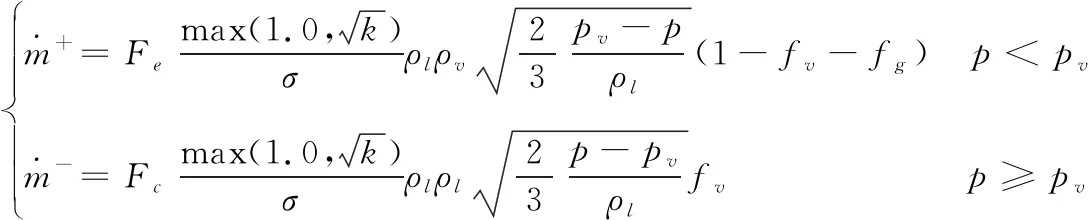
(9)

1.4 可压缩液体模型

Tait方程是通过采用非线性回归的方法，对能够反应p-v-T三者关系的试验数据进行拟合，而得到的液体状态方程，广泛应用于描述可压缩液体的物性。没有温度修正的简化Tait液体状态方程可描述为：

(10)

K=K0+nΔp

(11)

Δp=p-p0

(12)

(13)

式中:p0为参考压力；ρ0为参考压力下的液体密度；K0为参考压力下的液体体积弹性模型；n为密度指数；p为当前压力；ρ为当前压力下的液体密度；K为当前压力下的液体体积弹性模量；c为水中声速。

1.5 动网格技术

高速射弹在空泡中的运动是由作用在弹上的流体动力、力矩以及其他力共同决定的，耦合运动即射弹运动与空泡流场的计算相互耦合。已知前一时刻刚体重心位置和，软件通过对物体表面压力和剪切应力积分得到流体动力和力矩，再根据刚体运动方程计算物体运动的平移速度和角速度，然后重新计算重心位置和。

(14)

(15)

式中G为变换矩阵，刚体的位置与方向根据每时间步线速度和角速度的变化而变化。

采用移动计算域技术模拟弹体运动，计算过程中仅涉及计算域的移动，不存在网格的变形与重构，计算效率高，结果一致性好。运用该种动网格方法可以基于刚体空间运动方程和实时流体动力实现多自由度运动解算。

2 计算模型及方法验证

2.1 计算模型及边界条件

本文所研究的射弹模型如图1所示，射弹采用圆盘空化器，前部为两段锥段，中间为圆柱段，柱段尾部安装有六片尾翼，以射弹质心为坐标原点，其参数如表1所示。

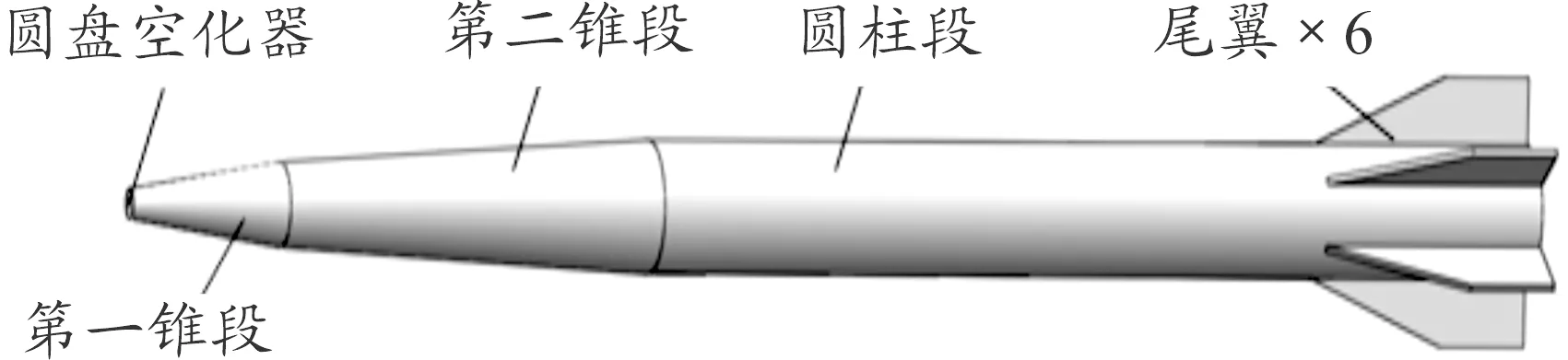
图1 射弹模型示意图

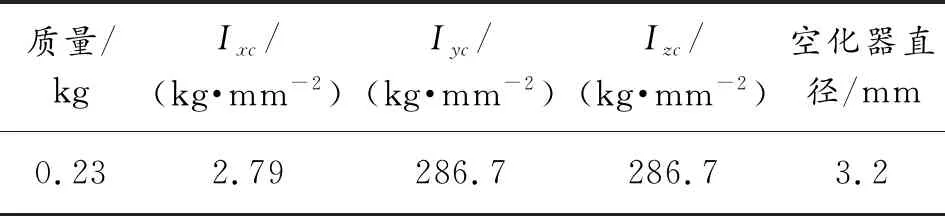
表1 射弹参数

采用圆柱形计算域，直径取50倍尾截面空泡直径，计算域轴向长度为11倍弹长，前端边界距离空化器4倍弹长，后端边界距离弹尾6倍弹长，该计算域径向尺度可以忽略空泡阻塞效应[13]。

针对所建立的三维计算域，采用ICEM软件的O-Block技术划分全结构化网格，如图2所示在弹体周围3 mm范围内的流域划分外O-block用于设置边界层网格，近壁面添加边界层网格，并根据y+值对网格进行优化。划分网格时特别注意在空泡两相交界面位置进行网格加密，最终划分的网格总数约80万，网格质量均在0.6以上。

图2 网格划分图

计算域四周边界均设置为压力入口条件(pressure-inlet)，设置静压值且静压值随深度变化，射弹表面的边界条件设置为壁面(wall)，并且壁面与临界网格相对静止。计算域和边界条件设置如图3所示。

图3 计算域及边界条件示意图

2.2 数值方法验证

郭子涛[14]对平头柱体入水过程进行了实验研究，利用高速相机记录了柱体以603 m/s水平入水过程的空泡形态，并推导出了柱体入水速度衰减特性。本文基于建立的三维数值模型，采用与文献[14]相同的三维柱体模型及初始条件模拟水平入水过程，仿真结果与实验数据如图4、图5所示。

图4 603 m/s水平入水实验与仿真空泡轮廓

图5 速度随时间变化曲线

图4为长度25.4 mm的柱体入水实验与仿真空泡大小，可以看出在同一时间节点下实验与仿真得到的不同部位的空泡直径偏差很小，图5为实验与仿真速度衰减曲线，减速特性基本一致，最大误差小于10%。由此可知，试验结果与数值仿真结果吻合很好，数值模型具有一定的准确性。

3 计算结果及分析

3.1 升阻力及空泡形态研究

对于采用滑膛炮发射的尾翼稳定超空泡射弹，入水过程可以按照单平面3自由度运动处理，以攻角为变量，探究入水瞬间升阻力特性及空泡形态的变化规律。射弹垂直入水速度1 000 m/s，无初始俯仰角速度，考虑水的压缩性，初始攻角分别取0°、1.5°、3°。

图6至图8分别表示射弹0°、1.5°、3°攻角入水不同距离对应的空泡形态，L为弹长，不同攻角下的入水空泡差异显著。0°攻角入水时，除空化器外其余部分均不沾湿，空泡沿弹体轴线对称，随着入水距离的增加自由液面对空泡形态的影响逐渐减弱，入水1.25倍弹长后弹身附近空泡形态基本保持不变。1.5°攻角入水时，入水距离小于1倍弹长时弹体不沾湿，超过1倍弹长之后仅尾翼发生沾湿，射弹壁面的挤压导致弹体两侧的空泡呈现出不对称性，尾翼沾湿后产生二次空泡。3°攻角入水时，弹体第二锥段入水即沾湿，入水距离超过1倍弹长之后尾翼及其附近的弹身沾湿，空泡不对称性加剧，尾翼拉出的二次空泡更大。入水攻角越大，自由面受到砰击产生的飞溅更明显。分析结果可知，入水两倍弹长时弹体空泡外形特征和阻力特性均趋于稳定，自由液面对弹体空泡基本无影响，此时可认为超空泡射弹的入水弹道结束并转入水下弹道。

图6 0°攻角入水空泡发展过程示意图

图7 1.5°攻角入水空泡发展过程示意图

图8 3°攻角入水空泡发展过程示意图

图9为不同攻角垂直入水时以弹体为研究对象的冲击阻力曲线，在空中运动段阻力很小，0.002 ms后射弹开始入水，阻力迅速增大，0.003 ms冲击阻力达到峰值，此后阻力不断减小，标志着入水空泡流动趋于稳定。3种攻角的冲击阻力曲线基本重合，仅峰值有微小差异，攻角影响弹体的沾湿面积进而影响冲击阻力峰值，0°和1.5°攻角沾湿面积相近，阻力峰值相差不大，3°攻角空化器表面沾湿区域较小，但空化器边缘相接的锥段沾湿面积较大，因此阻力峰值最大，峰值出现的时间较触水时间略微延后。不同攻角的冲击阻力峰值约为稳态阻力的9倍，冲击曲线脉宽基本一致，表明攻角对射弹入水冲击峰脉宽影响极小。

图9 0°、1.5°、3°攻角入水冲击阻力曲线

图10为1.5°、3°攻角弹体垂直入水冲击升力曲线，入水瞬间升力曲线同样出现峰值，且峰值出现时间较阻力峰值延后，入水攻角越大，冲击升力越大，3°攻角升力峰值约为1.5°攻角的2倍。

图10 0°、1.5°、3°攻角入水冲击升力曲线

3.2 变攻角入水弹道特性研究

以地面系为参考坐标系，射弹沿X方向垂直入水，分析弹体在入水过程中的纵平面弹道特性，由于0°攻角入水时弹体理论上不发生偏转且无侧向速度，因此本节主要比较1.5°和3°攻角下的弹道参数变化，以入水距离1 m(6倍弹长)作为计算终止条件。

在纵平面上，攻角为弹体速度方向与弹轴方向的夹角，因此初始攻角等于初始俯仰角。射弹带攻角入水时，攻角扰动引起弹体空泡的不对称，导致弹体侧向受力不同，弹体在力的作用下姿态偏转，在空泡内做周期性震荡运动，即尾拍效应。图11显示，两种攻角弹体入水俯仰角均先减小后反向增大，处于尾拍形成过程。不同攻角沾湿位置不同导致弹体受力不同，俯仰角幅值及摆动周期存在差异。射弹1.5°攻角入水时只有尾翼沾湿，侧向受力较小，俯仰角变化幅度较小，3°攻角入水时弹体第二锥段和尾翼均沾湿，侧向受力较大，因此摆动周期较小，俯仰角变化幅度较大。

图11 俯仰角随时间变化曲线

图12显示，两种攻角条件下，弹体的俯仰角速度呈先增大后减小再反向增大的震荡变化趋势。攻角越大，俯仰角速度幅值越大，震荡周期越小，3°攻角的最大俯仰角速度约为1.5°攻角下的2倍，俯仰角速度的演变规律与俯仰角变化特性相符。

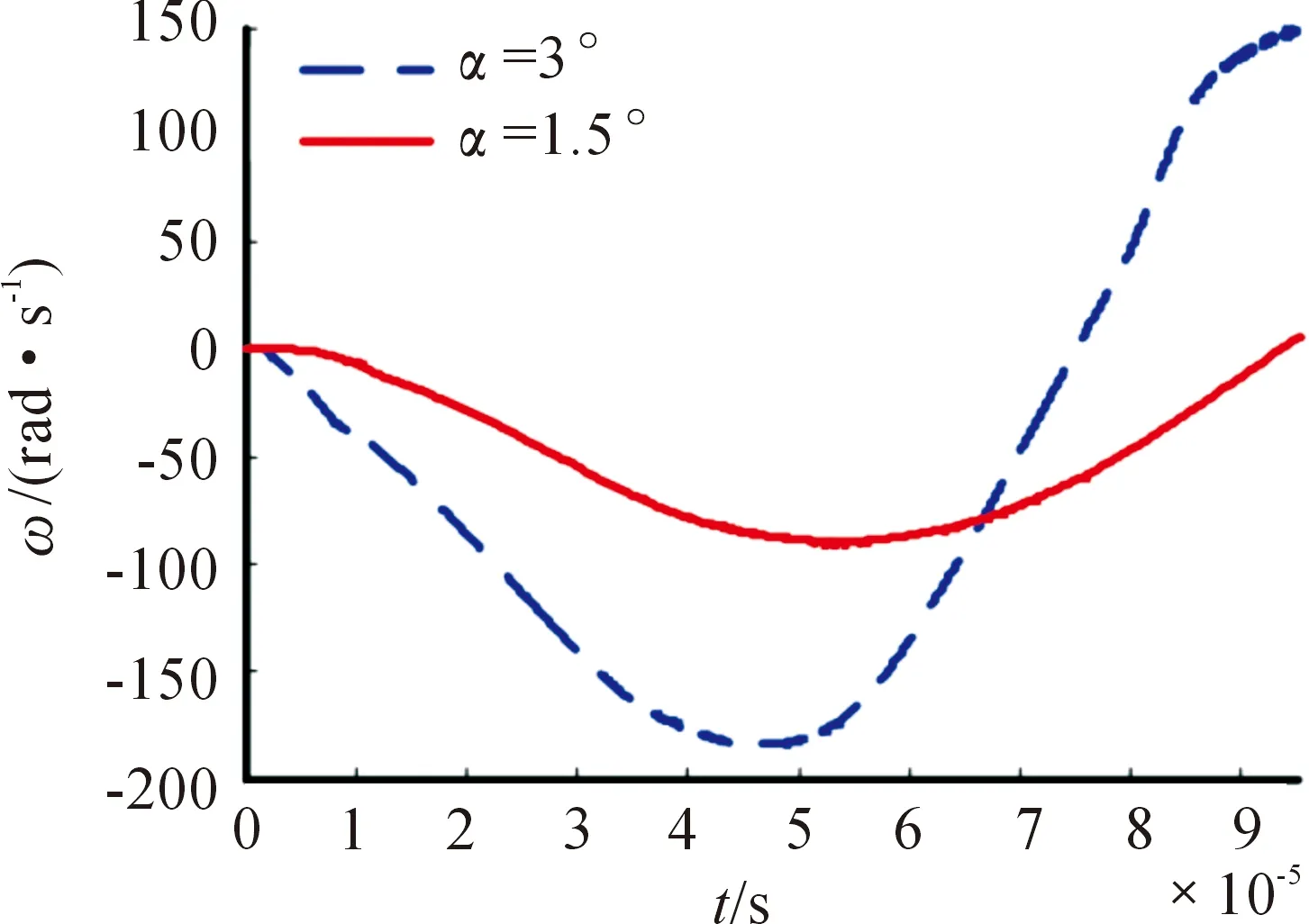
图12 俯仰角速度随时间变化曲线

图13显示，入水初期3种攻角的轴向速度均呈单调递减规律变化，攻角和射弹轴向横截面积越大，阻力越大，从而速度衰减幅度越大。

图13 轴向速度随时间变化曲线

图14显示，初始攻角扰动引起弹体在空泡内摆动，导致侧向速度变化，两种攻角的侧向速度均呈先增大后减小再反向增大的震荡变化规律，攻角越大，弹体侧向受力越大，侧向速度幅值越大。

图14 侧向速度随时间变化曲线

不同攻角下射弹入水6倍弹长时轴向速度衰减与初速相比均处于较小量级，在探究射弹入水空泡形态变化时可不考虑弹体速度变化。

图15显示，射弹以1.5°和3°攻角垂直入水时，由于弹体沾湿，使姿态发生偏转，质心均产生了侧向位移。入水攻角越大侧向位移越大，质心位移变化与弹体姿态变化紧密相关。

图15 质心位移曲线

4 结论

1) 不同攻角入水弹体沾湿部位及姿态变化具有差异，空泡具有不对称性；入水攻角越大，自由面受到砰击产生的飞溅更明显；入水两倍弹长后弹体空泡外形特征和阻力特性均趋于稳定，自由液面对空泡基本无影响，此时的入水弹道与水下弹道无异。

2) 不同攻角的冲击升阻力特性变化规律基本一致，攻角影响弹体的沾湿面积进而影响冲击阻力峰值，弹体冲击升力随攻角增大而增大，射弹入水冲击峰脉宽不受攻角影响。

3) 弹体带攻角入水时尾拍特性不可忽略，攻角越大，弹体轴向速度衰减幅度越大，俯仰角、俯仰角速度及侧向速度幅值越大，模拟结果可为超空泡射弹的全弹道设计提供参考。