好材料,是深度学习的前提
2020-08-04涂玉霞


【摘 要】要凸显数学学科的价值,须从本质出发,选择合适的学习材料,帮助学生进行深度学习,把零碎的知识点变成丰富的模型,继而形成数学素养。“3·14型思维拓展学习材料”的原则、宗旨和特征,诠释了选择数学学习材料的基本策略。
【关键词】深度学习 原汁数学 学习材料
湖北省武穴市师范附属小学校长,数学正高级教师,华中师范大学教育硕士,教育部名师领航工程成员,提出原汁数学教学理念。湖北省第十一次党代会党代表,湖北省特级教师,湖北名师,湖北名师工作室主持人,湖北省第二批卓越校长培养对象,湖北省国培专家库成员,湖北教科院、湖北师范大学兼职研究员,黄冈师范学院兼职硕士生导师,荣获“中国好校长”“湖北省三八红旗手”“黄冈市五一劳动奖章”等奖项。
数学到底是一个什么样的学科?它在人的发展中承载着什么样的光荣使命?我认为有三个核心点:解决实际问题、完善思维模式、带来精神愉悦。这也是我们所倡导的原汁数学的教学价值观—从本质出发,让学习变得自信自主,有趣有效。要实现这种价值观,必须选择合适的学习材料,进行深度学习,把零碎的知识点变成丰富的模型,继而形成数学素养。
那么什么样的材料,才能引发学生深度思考,让学生进入深度学习状态呢?原汁数学研究团队这些年来致力于开发“3·14”(“3”点原则,“1”个宗旨,“4”种特征)型思维拓展素材。不再只是限于教材中的例子,而是从现实生活、数学史话、趣题、魔术、游戏中去挖掘丰富多样、富有启迪的材料,使学生能够运用数学的眼光与思维,去认识世界、理解世界和表达世界。
一、“3”点原则:新鲜点,贴近点,本质点
教学最重要的不是在于教师讲了多少,而是在于学生学了多少。儿童注意力集中时间短,喜欢新鲜生动的、易于理解的知识,因此,我们要遵循儿童的学习特点和数学学习特征,尽量为学生选择新鲜生动、接近其最近发展区、凸显数学本质的材料。
【案例1】像爱迪生那样思考(人教版六年级下册“运用圆柱体积计算解决问题”,涂玉霞工作室陈天平老师提供)
学习材料1:脑筋急转弯(见图1)。倒过来看,不难发现是87(见图2)。教师及时总结,这种“倒过来”的思考方法突破思维定式,在生活中有很大的作用。
学习材料2:求一个空啤酒瓶的容积。
核心问题1:如果让你求出这个空啤酒瓶的容积,你有什么办法吗?
生1:将啤酒瓶加满水,然后将水倒入一个量杯中,量出的水的体积就是啤酒瓶的容积。
师:真是一个不错的方法。大家知道这个方法了吗?他是受到了什么启发想到这个方法的呢?
生2:爱迪生教他的助手测量灯泡的容积的方
法。(学生介绍爱迪生测量灯泡容积的方法)
师:大家说说看,爱迪生的方法巧妙在哪?
生3:把啤酒瓶的容积转化成水的体积,水的体积可以通过量杯测量出来。
核心问题2:如果啤酒瓶里不加满水,只加一部分水也能求出啤酒瓶的容积吗?
讨论:(1)这时水的体积是不是啤酒瓶的容积?
(2)你需要测量哪些数据,求出啤酒瓶的容积?
啤酒瓶的容积=(水)的体积+(瓶子倒过来后上部空出来的部分)的容积(见图3)
核心问题3:是不是只要瓶子里有液体,无论它有多少,都能求出瓶子的容积呢?
教师通过液面不断上升的动态演示,使学生明白当液面的高度超过瓶子的颈线位时,瓶子里的液体将变成不规则图形,运用此方法无法求出其容积(见图4)。
当液面不断下降,倒过来之后液面的高度低于瓶子的颈线位时,这时空的部分仍然是不规则图形,此方法也求不出它的容积(见图5)。
这样的学习材料就很有意思。
第一,以停车场的脑筋急转弯进入,“倒过来”的思考角度为后面的学习做了很好的铺垫。
第二,把爱迪生的转化思想进一步深入,如果把水倒出去,用什么方法来测量?以“倒过来”的思路,把不规则的体积变成规则的体积,充分体现了转化思想的灵活性。
第三,拋出“如果啤酒瓶里不加满水,只加一部分水也能求出啤酒瓶的容积吗?”问题后,让学生懂得“这一部分水”是有限制条件的,只有这样才算完整解决问题,同时也渗透了函数思想—自变量是有取值范围的。
在传统教学中,教师往往只给学生相关数据,把教学停留在让学生算出啤酒瓶的容积上,好比是给学生一把钥匙,让他去开门,是一种机械动作。而陈天平老师提供的教学案例,是在提供富有思维含量的材料的同时,从多个角度、多个层次展开问题解决的探究,整个教学过程都需要学生调动已有的知识和经验去解决问题,好比是给学生一串钥匙,让学生自己从中找到正确的那一把钥匙去开门,这属于一种智力活动。
二、 “1”个宗旨:思考真正发生,智慧真正生长
我们所选择的素材一定不会是哗众取宠,追求另类,而是让学生在这种思维碰撞中,获得乍现的灵光,全神贯注地投入学习中。
【案例2】撕纸也能计算(人教版六年级上册“分数加减法”,涂玉霞工作室周琴老师提供)
师:你能够在10秒内算出这个列式的结果吗?。(时间到,学生们都没有算出来。教师公布自己的口算答案,学生们羡慕)
师:如何挑战不可能?这里面肯定有奥秘。我们一起来玩个游戏吧。请小明同学来当我的小助手。(拿出一张A4纸)这是一张纸,平均分成两份,每份就是,给小明,我留下;再把我的平均分成两份,每份就是,小明拿,我拿;又把我的平均分成两份,其中给了小明,我留……一直这样分下去,分8次后,我手上还剩多少?小明手上有多少?小明手上有,老师手上有。原来一张纸就是一个1,分完之后,老师有,小明有多少?
学生们觉得特别惊奇,感叹“真简单!”。
师:那我们就来继续玩游戏:。能不能用刚才的方法,计算出来?(三个同学为一组,共同操作演示。很多同学因为受上面计算题的影响,把纸平均分成了两份,后来发现不对,改分成3份)
教师请学生上台演示:把一张纸平均分成3份,给小丽和小方每人都是,继续分下去,分了6次后,小丽有,小方有,我有,原来一张纸就是一个1,分完之后,我有,小丽有多少?
教师继续提问:如果不撕纸,我们还有没有其他简单的方法把它计算出来?
教师继续抛出问题:这种方法与撕纸有什么联系?(学生讨论)
是不是觉得很“烧脑”?看似非常复杂的计算题,却通过撕纸这样的方法,让它变得异常简单。它把一个个抽象的数变成了具象的小纸条,使计算过程看得见,算法理得清。教师又通过解法欣赏,进一步帮助学生打开了思路。选择合适的学习材料再加上独到的教学指导,使枯燥的计算也有了思考的深度和思想的厚度。
教学中,我们把握三个要领:第一,选择的材料难度应该略高于学生的现有水平,使学生愿意尝试;第二,要有普遍性和典型性,能够反映一般特征;第三,要能扩展开来,可以举一反三。
三、“4”种特征:联结性,发展性,挑战性,开放性
深度学习有五个层级(见图6),第一个层级没有发生学习,第二和第三层都是浅层学习。拿第三个层级来说,这样的学习就好比我们认识一个人,知道他的名字、长相和工作单位,但我们并不了解他,我们需要结合他的性格特征和工作经历来认识他,让学习达到第四级和第五级的水平,这就是深度学习。深度学习的材料只有尽可能实现联结性、发展性、挑战性、开放性,才能够建立整体结构。
【案例3】眼见为“实”吗?(人教版小学数学四年级上册“平行与垂直”)
师:看看下面带箭头的两条线段,猜猜哪条更长?(见图7)(学生们认为上面那条线段长,请一位学生上去量一量,结果是一样长!学生们感到很吃惊)
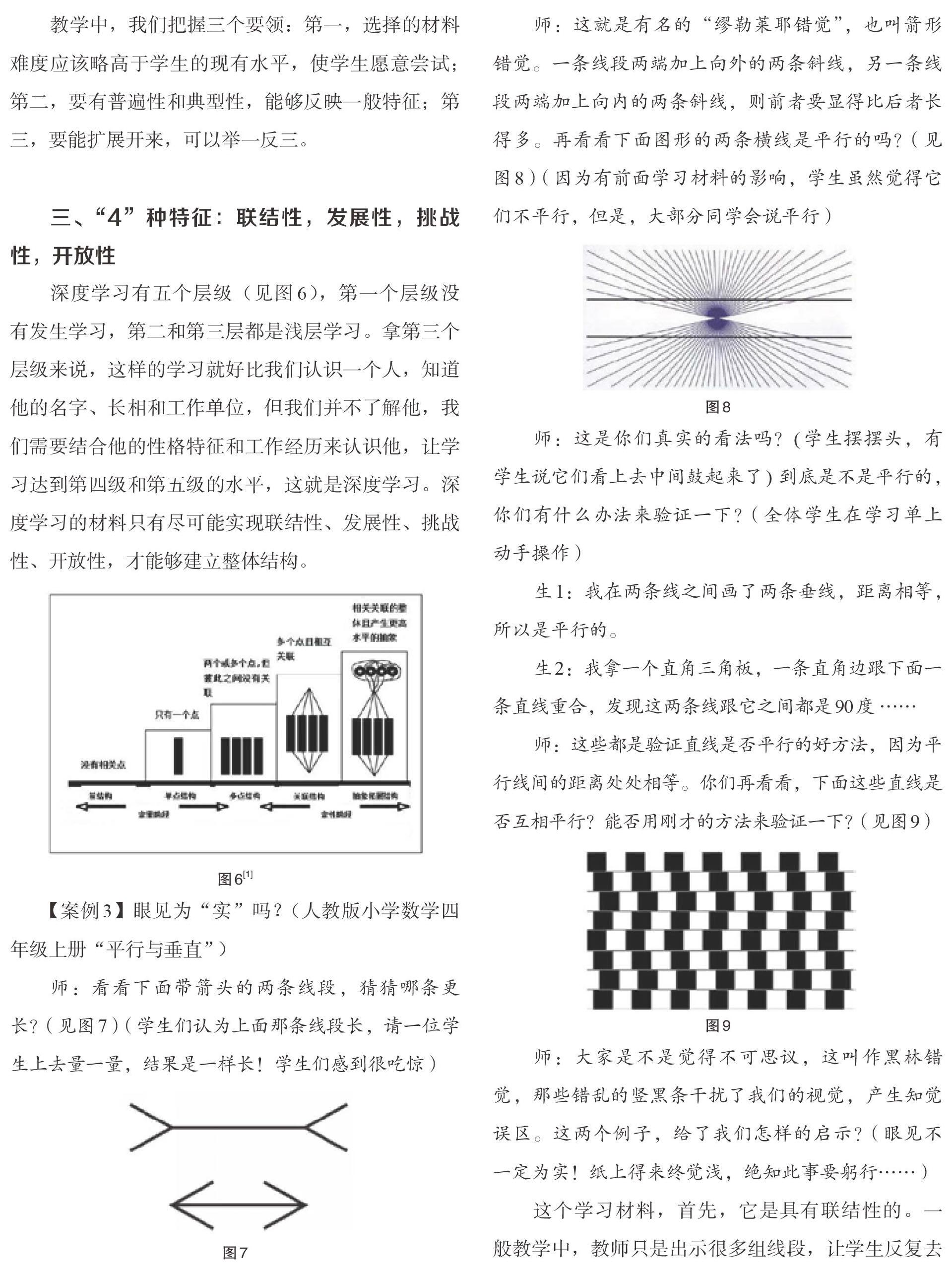
师:这就是有名的“缪勒莱耶错觉”,也叫箭形错觉。一条线段两端加上向外的两条斜线,另一条线段两端加上向内的两条斜线,则前者要显得比后者长得多。再看看下面图形的两条横线是平行的吗?(见图8)(因为有前面学习材料的影响,学生虽然觉得它们不平行,但是,大部分同学会说平行)
师:这是你们真实的看法吗?(学生摆摆头,有学生说它们看上去中间鼓起来了) 到底是不是平行的,你们有什么办法来验证一下?(全体学生在学习单上动手操作)
生1:我在两条线之间画了两条垂线,距离相等,所以是平行的。
生2:我拿一个直角三角板,一条直角边跟下面一条直线重合,发现这两条线跟它之间都是90度 ……
师:这些都是验证直线是否平行的好方法,因为平行线间的距离处处相等。你们再看看,下面这些直线是否互相平行?能否用刚才的方法来验证一下?(见图9)
师:大家是不是觉得不可思议,这叫作黑林错觉,那些错乱的竖黑条干扰了我们的视觉,产生知觉误区。这两个例子,给了我们怎样的启示?(眼见不一定为实!纸上得来终觉浅,绝知此事要躬行……)
这个学习材料,首先,它是具有联结性的。一般教学中,教师只是出示很多组线段,让学生反复去辨别是不是平行线,然后教师问“为什么是平行线”,这缺乏知识运用的现实价值。而原汁数学的学习,注重知识的融合和价值观的融合,如运用垂直来判断平行关系,通过错觉图例引发学生思考,培养正确判断事物的科学态度。其次,它具有发展性。从判断两条直线是否平行到判断众多条直线是否平行,更需要方法的巧妙运用,这对学生深层次理解平行很有好处。同时,它也是富有挑战性和开发性的。在矛盾冲突中,学生的好奇心和利用数学知识去解决问题的迫切愿望得以激发,学生获得了“跳一跳就可以摘到桃子”的愉悦感和成就感。
【案例4】你相信算命吗?(人教版六年级下册“抽屉原理”)
师:猜想一下,咱们武穴市有83万人,有没有人会在同一天出生?
生齐:肯定有!
师:那至少会有多少人在同一天出生呢?(学生思考,借助计算题解答)
师:这是属于哪类问题?
生1:抽屉原理。一年最多366天,按照最不利原则,我们假设有366个抽屉。830000÷366=2267(人)……278(人)。每个抽屉里装2267个人,还有278人,那么也就是说至少有2268人在同一天出生。
师:再进一步思考,至少有多少人会在同一时出生呢?
生2:一天24个小时,相当于24个抽屉。2268÷24=94(人)……12(人)。至少有95人在同月同日同时出生。
师:武穴至少有95人在同月同日同時出生,那么他们的命运和性格应该是相同的,对不对?
生3:我觉得不大可能。
师:但是我们常常看到一些心理测试,还有一些星座算命,都说只要知道生日或出生的时辰,就能够算出他的性格和命运。而且,还有很多人说,算得特别准。这是什么原因?其实并不是因为算得准确,而是因为我们常常更倾向于相信一些笼统而普遍的人格描述。这些特点的描述既空洞又模糊,但是人们很容易接受这些描述,这也就是心理学上说的福勒效应。
延伸练习:人类的头发依种族和发色的不同,数量也略有差异。黄种人约有10万根;长有金色头发的白种人头发较细,约有12万根;红色头发略粗,有8万~9万根。83万的武穴人中至少有多少人的头发根数一样多?
这组学习材料的特点在于,能够结合生活中的现实问题,让学生运用抽屉原理来加以解决,有实际价值。同时,以数据来破解迷信,帮助学生树立正确的世界观,体现了“大数学观”。
好的学习材料正如一首好诗,总能触及人的心灵,让人进行类比联想。正如这首小诗所写,我忘记了作者是谁,不过诗的内容我却是一句也忘不了。
数学的味道和巧克力的味道一样
甜中带点苦
苦中带点甜
只有细心品味的人 才能知道 它真正的滋味
学数学的意义 不在于它的用处
而在于你忘我的投入
重点不是 花多少时间做数学
而是你花多少时间让自己
变得喜欢做数学
参考文献
[1] 约翰 B.彼格斯,凯文 F.科利斯.学习质量评价:SOLO分类理论(可观察的学习成果结构) [M]. 高凌飙,张洪岩,译. 北京:人民教育出版社,2010:78.
责任编辑:孙昕
heartedu_sx@163.com
