特殊矩阵特征值的Wielandt-Hoffman-残差型扰动界

孔祥强(菏泽学院 数学与统计学院，山东 菏泽 274015)

矩阵特征值的扰动问题是矩阵扰动分析的重要方向。A表示原始矩阵，B表示扰动后的矩阵，对于A和B同阶的情形，研究成果已相当丰富。当A与B不同阶时，对于这种矩阵特征值的残差扰动界的研究，部分成果可参见文献[1-3]。文献[4]研究了不变子空间上可对角化矩阵及可对称化矩阵的残差扰动界。文献[5]研究了Hermite矩阵与可对称化矩阵特征值的Weyl-残差型扰动界。本文继续研究Hermite矩阵及可对称化矩阵特征值的扰动，得到新的Wielandt-Hoffman-残差型扰动界。

1 预备知识

引理1[8]设A,B∈Cn×n均是Hermite阵，Q∈Cn×n是Hermite正定阵，其特征值γ1≥γ2≥…≥γn，c是任意正数，则

其中

2 主要结果

定理1设A∈Cn×n为Hermite阵，即存在酉阵P，使A=PΛ1P-1，Λ1=diag(λ1,…,λn)；B∈Cm×m为可对称化矩阵，即存在可逆阵Q，使

为列满秩阵，Σ=diag(σ1,…,σm)，σ1≥…≥σm，则存在1,…,n的某个排列π，使得

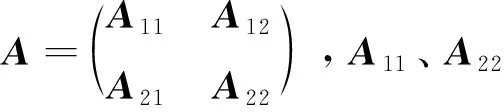
(1)

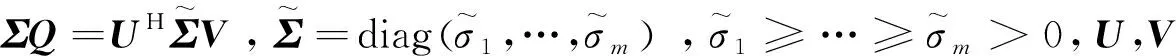
(2)

故

(3)

(4)

由引理1，

将式(2)、(3)、(4)代入上式，得

(5)

(6)

将式(5)、(6)代入(1)，得

由引理2，存在1,…,n的某个排列π，使得

故

注1①不难看出，n=m时，定理1仍成立，即为文[10]中结论。故定理1是文[10]中结论的推广。

定理2设A∈Cn×n，B∈Cm×m均为可对称化矩阵，即存在可逆阵P,Q，使得

A=PΛ1P-1，Λ1=diag(λ1,…,λn)，

B=QΛ2Q-1，Λ2=diag(μ1,…,μm)，

(7)

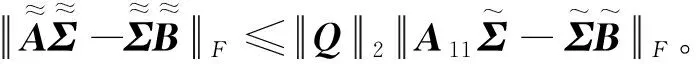
(8)

故

(9)

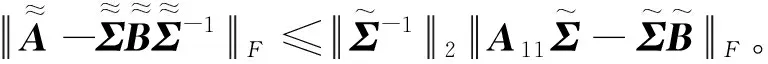
(10)

依引理1，

将式(8)、(9)、(10)代入上式，得

则

(11)

(12)

将式(11)、(12)代入(7)，得

依引理2，存在1,…,n的某个排列π，使得

所以

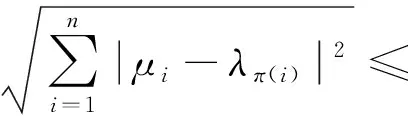
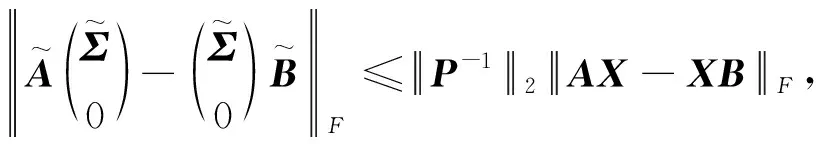
故

②若A为Hermite阵，则K(P)=1，结论即为定理1。因此定理2比定理1 更强。

③若A,B均为Hermite阵，X为单位阵E，则结论即为Wielandt-Hoffman定理。故定理2是Wielandt-Hoffman定理的推广。

3 结语

本文探讨了Hermite阵和可对称化矩阵特征值的残差型扰动上界。以此为基础，可进一步研究正规矩阵和可对角化矩阵特征值的扰动界，进而研究原始矩阵及其扰动后的矩阵均为任意矩阵的情形。