等离子体电弧激励器特性及减阻的仿真研究
2020-08-04陈伦江
袁 野,赵 青,陈伦江,薄 勇
(电子科技大学, 成都 611731)
0 引言
高超声速飞行器在不改变外形的前提下,通过主动流动控制技术在飞行器局部增升减阻,是最为有效可行的技术方案之一。等离子流动控制技术是基于等离子体气动激励的新概念主动流动控制技术,它利用等离子体作为能量载体向局部流场施加扰动,引起局部流场状态与特性的变化,从而改变飞行器的局部升阻力或力矩,实现对飞行器的流动控制。
国内外学者对等离子体流动控制做了广泛的研究。俄罗斯航天局利用电弧逆向喷流激励器在Ma=4的来流中实现了43%的减阻[1-2]。美国空军实验室仿真发现由于等离子体热效应,在Ma=6的来流中将产生大于12.5%的减阻,减阻主要来源于逆向射流的黏性-非黏性相互作用和热能沉积[3-4]。德克萨斯大学利用等离子体合成射流激励器实现了射流速度300 m/s,在Ma=3的来流中使分离冲击向下游移动约1/4边界层厚度[5]。霍普金斯大学、佛罗里达州立大学利用等离子体合成射流激励器在Ma=1.5交叉流中产生5°转向角[6]。日本东京大学用表面电弧激励器在Ma=7来流中仿真得到阻力系数减小13.1%,实验得到阻力减小23%的结论[7]。美国圣母大学利用浅腔式电弧激励器在Ma=4.5来流中实现了更早的层流-湍流过渡并且防止压缩斜坡上的分离[8]。空军工程大学用表面电弧激励器在Ma=2来流、26°压缩斜坡中产生控制气体气泡(CGBs),CGBs将冲击波的足部区域移除[9]。国防科技大学用等离子体合成射流激励器在Ma=5来流、25°压缩斜坡中使冲击角减小3°[10]。
这些研究已取得了初步的进展,但是模拟激励器减阻效果时,能量源项的加入多用估计的方法,从输入功率估计热源项的值。而本文采用包括电流、磁场、层流和流体传热在内的多物理场有限元方法对激励器的工作特性进行了数值模拟,得到了激励器准确热源分布。将此热源项加入能量方程,计算减阻效果,得到更准确的结果。
1 物理模型和方程
假设电弧等离子体为局部热力学平衡LTE状态,电子和重离子温度相等,不考虑重力。电弧等离子体在光学上被看作一薄层,不考虑电弧对辐射的吸收,运用净发射系数计算辐射损失,气体被假设为弱可压缩。
对于层流和弱可压缩氩气流,质量连续方程、动量Navier-Stokes方程和能量方程为
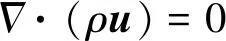
(1)
(2)
(3)
式中,ρ和η分别是流体的密度和动力黏度。u是流体速度,p是压强,I是单位张量。F是体积力,包括洛伦兹力FL。T,k,Cp和Q分别是温度、热导率、定压比热容和热源。其中Q包括焦耳热项QJ、电子焓输运项及由净体积发射系数计算的体积净辐射损失项。FL和QJ分别为
FL=J×B
(4)
QJ=J·(E+u×B)
(5)
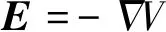

(6)
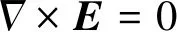
(7)
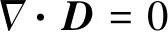
(8)
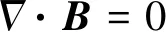
(9)
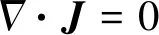
(10)
本文设计了一种激励器-表面电弧放电激励器。电弧激励器模型为二维阴极阳极表面结构,计算区域为阴阳极表面向上的三维立体开放区域,其结构如图1所示。阳极和阴极材料均为钨。矩形区域为空气,空气上边界和四周边界为压力出口边界条件。求解区域一共有2.9×103个域单元。选择全耦合方法,利用MUMPS直接求解器对模型方程进行数值积分。同时,对电导率最小值采用参数化扫描,来改善计算的收敛性。
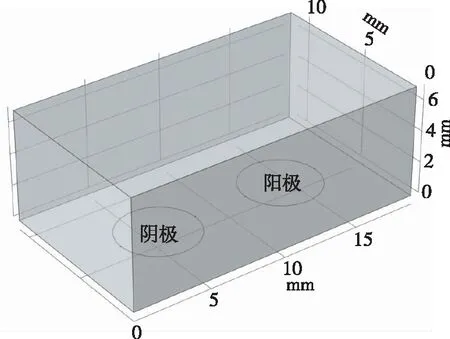
图1 表面电弧激励器结构图Fig.1 Structure of surface arc actuator
为了考查激励器的减阻效果,在一斜坡前方放入激励器,斜坡置于高超声速来流中,攻角为0°,模型如图2所示。需要求解带有斜坡的壁面区域的减阻效果。求解器为二维平面、基于密度的稳态求解器,启用能量方程。湍流模型为包含一个方程的Spalart-Allmaras模型,来流入口给定速度入口边界条件,出口给定压力出口边界条件,壁面给定无滑移边界条件。采用结构化网格,网格数为5万。控制方程的线性化采用显式形式。采用Roe-FDS流动格式。
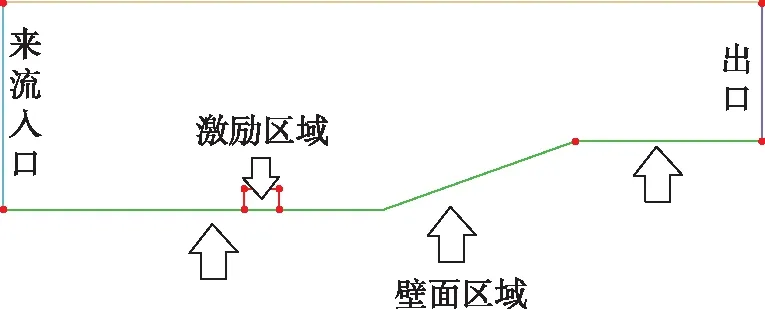
图2 减阻效果仿真模型图Fig.2 Simulation model of drag reduction effect
2 结果分析
2.1 表面电弧激励器
2.1.1 电势分布
电流7 A、阴阳极距离3 mm时的电势分布图如图3所示。阳极电势接近0 V,阴极为电势最低处,电势-84.75 V。在计算空间内电势值在-50~-30 V之间,在接近阳极和阴极处电势快速变化至最大最小值,电场强度在接近阴阳极处很大。
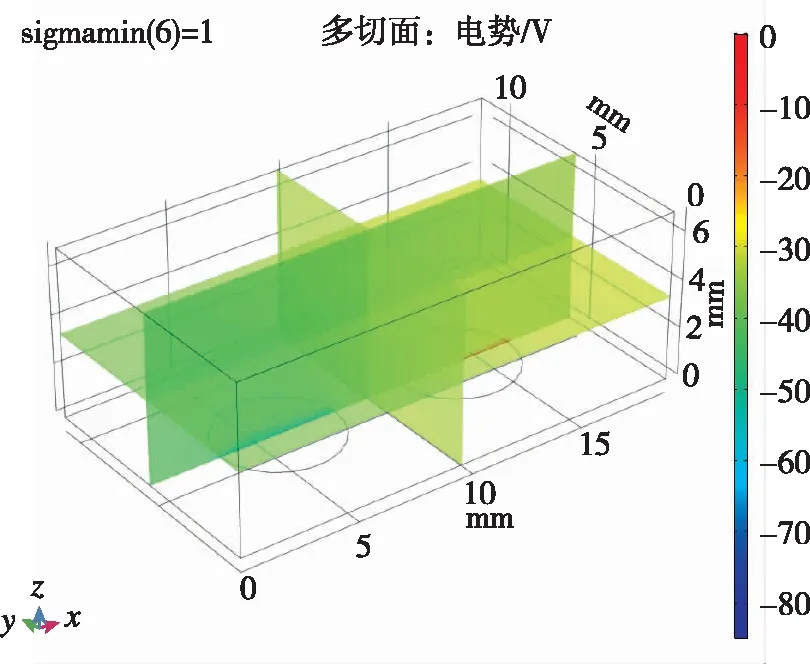
图3 电流7 A、阴阳极距离3 mm时的电势分布图Fig.3 Potential distribution when the current is 7 A and the distance between anode and cathode is 3 mm
2.1.2 温度分布
电流7 A、阴阳极距离3 mm时的温度分布图如图4所示。阳极、阴极为温度最低处。在计算空间内温度值在5 500~6 449 K之间,温度梯度绝对值在接近阴阳极处很大。阴极和阳极之间加瞬时脉冲高压,大量气体被击穿,产生电弧放电,主要由于电流产生的焦耳热的影响,产生大量热量,温度剧烈升高。阴阳极处由于温度不能高于材料熔点,加了边界条件。
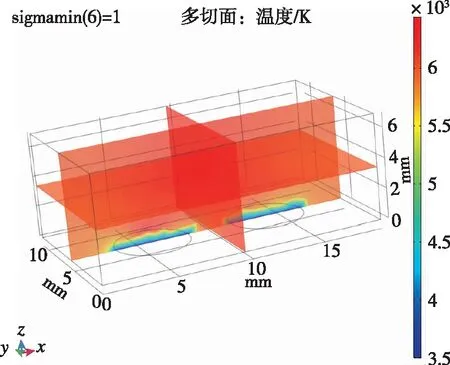
图4 电流7 A、阴阳极距离3 mm时的温度分布图Fig.4 Temperature distribution when the current is 7 A and the distance between anode and cathode is 3 mm
2.1.3 热源分布
从表15知,p=0.000<0.01,回归模型非常显著.但是从表16中看到,系数b1,b2,b3,b4相应的显著性概率均大于0.05,所以没有一个变量在模型中是重要变量,因此需要对变量进行筛选,采用逐步回归法重新建立回归模型.方法是在前面四步的基础上,增加:
电流7 A、阴阳极距离3 mm时的总热源分布图如图5所示。阴极表面附近为热源值最大处,高达9×1010W/m3以上。阳极表面附近热源3×1010W/m3左右,空间其余部分热源为2×1010W/m3以下。
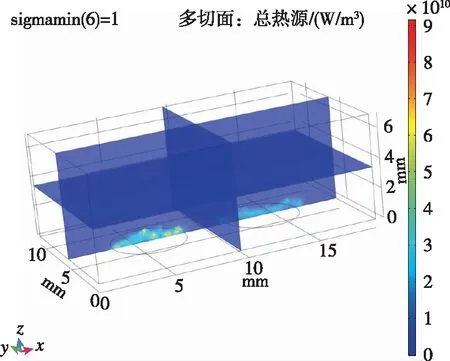
图5 电流7 A、阴阳极距离3 mm时的热源分布图Fig.5 Heat source distribution at 7 A current and 3 mm distance between anode and cathode
y=5.5 mm,z=0.2 mm时热源在不同电流下的分布如图6所示。热源在阴极表面大于阳极表面,在阴极表面高热源的x坐标范围小于阳极,且阴阳极距离近的内侧比距离远的外侧热源高。这可能是因为阴极设置为垂直于表面发射电流,而阳极电流可以是任意方向,因此在阴极表面高电流密度的x坐标范围小于阳极,总电流在阴阳极上是相等的,电流密度在阴极表面大于阳极表面。由温度分布图5可以看出,温度在阴阳极相差不大,电导率相差不大,焦耳热和电流密度平方成正比。热源主要部分是焦耳热,因此热源在阴极表面大于阳极表面,在阴极表面高热源的x坐标范围小于阳极。由于阴阳极距离近的内侧比距离远的外侧电场强度高,因此内侧比外侧电流密度大,内侧比外侧热源高。由图6可以看出,随电流的增大,热源值整体增大。
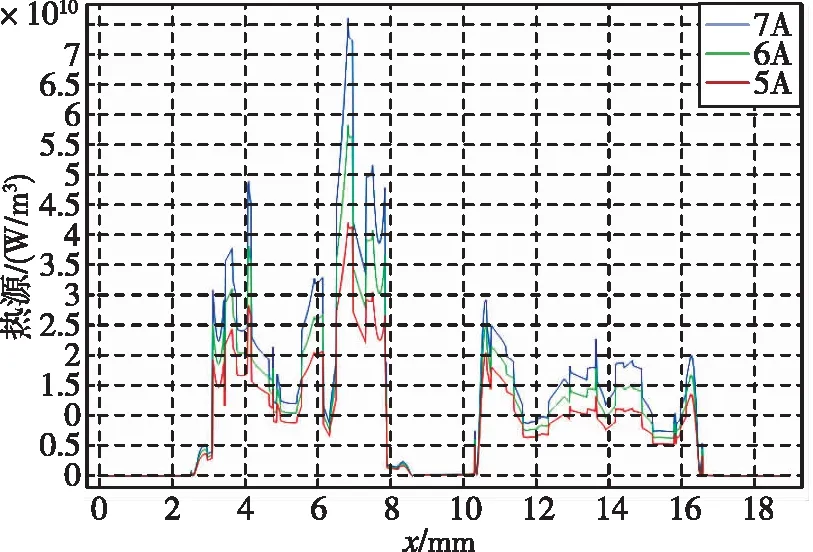
图6 y=5.5 mm,z=0.2 mm时热源在不同电流下的分布Fig.6 Distribution of heat sources under different currents when y=5.5 mm and z=0.2 mm
y=5.5 mm,z=0.2 mm时热源在不同阴阳极距离下的分布如图7所示。阴极的变化比较复杂,没有特定的规律。阳极随着阴阳极距离的增大,热源分布更趋均匀,内侧和外侧的差值减小。这是因为随着距离的增大,内外侧由场强产生的电流密度差别减小。
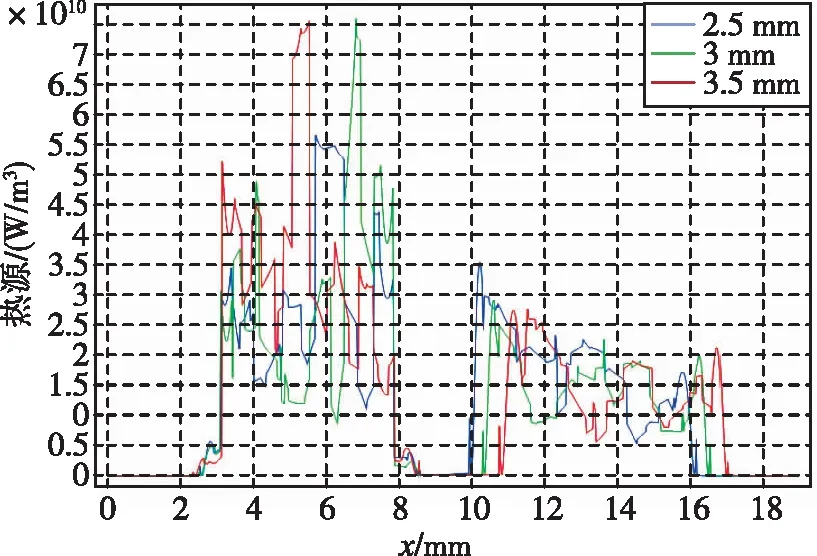
图7 y=5.5 mm,z=0.2 mm时热源在 不同阴阳极距离下的分布Fig.7 Distribution of heat sources at different anode and cathode distances when y=5.5 mm and z=0.2 mm
2.2 优化分析
表面电弧激励器各参数仿真结果如表1所示。等离子体电弧激励器的设计目的是得到最高的热源。电流7 A、阴阳极距离3.5 mm的表面电弧激励器为最优,因此在后面的减阻效果分析中采用此种表面电弧放电激励器。
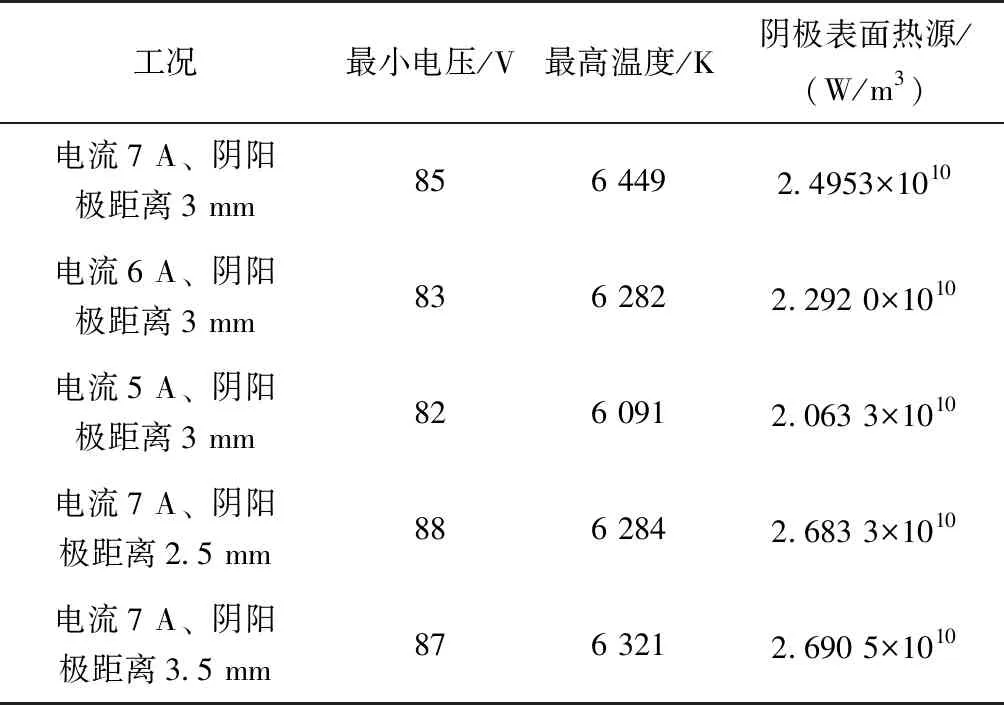
表1 表面电弧激励器仿真结果
2.3 电弧等离子体在超高声速飞行器中减阻效果研究
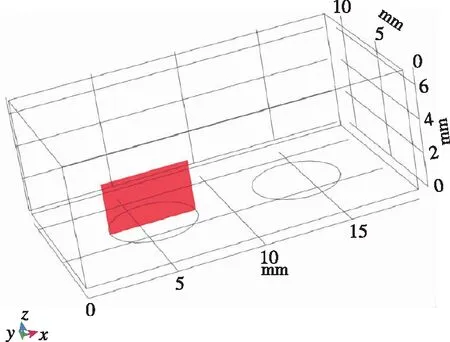
图8 所取热源截面Fig.8 Cross section of the heat source
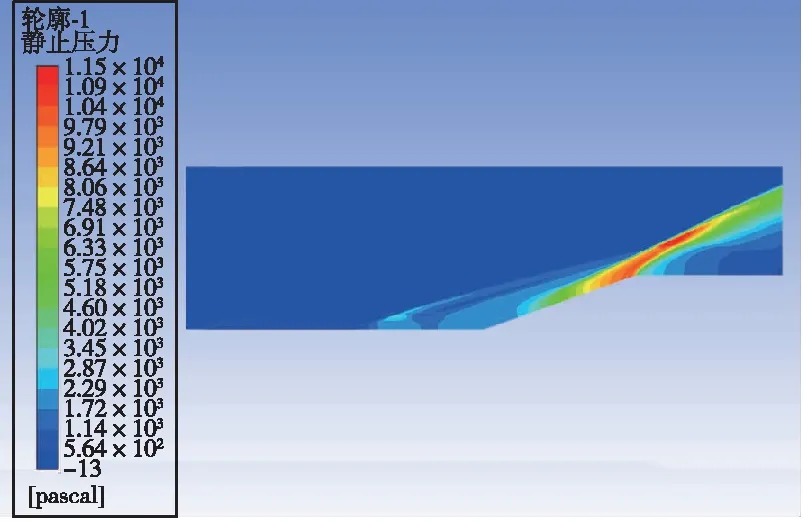
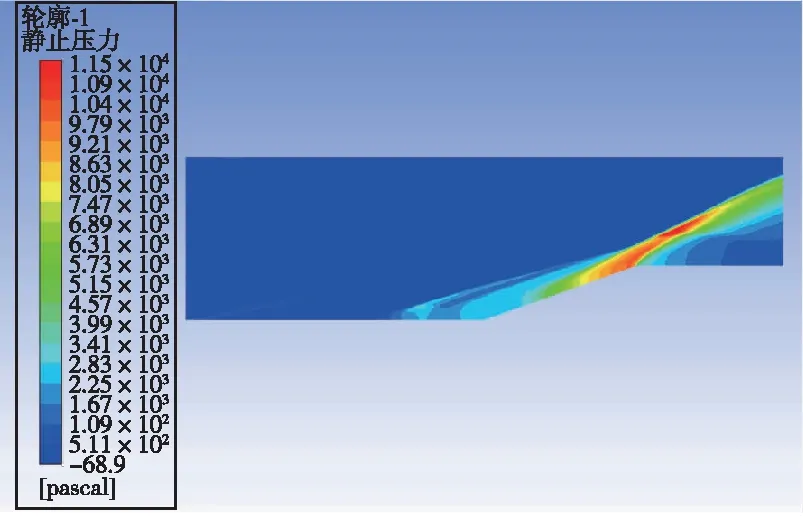
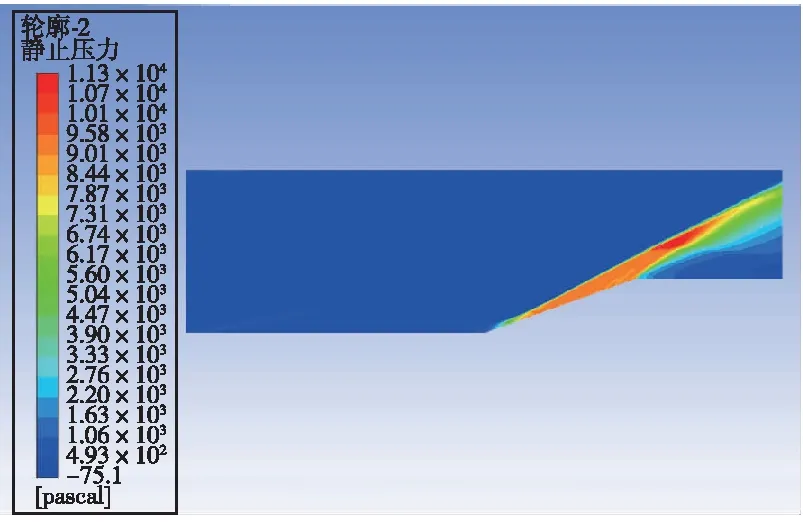
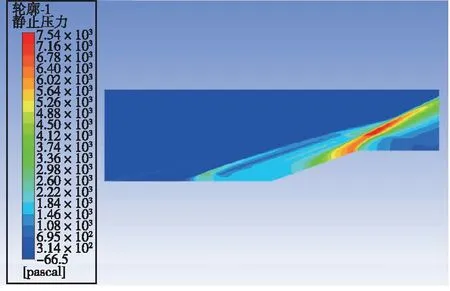
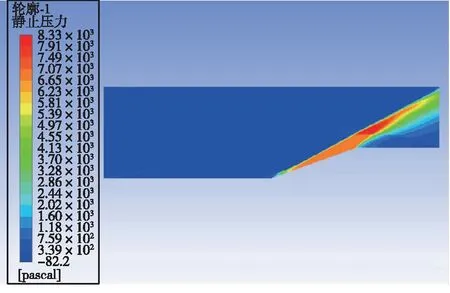
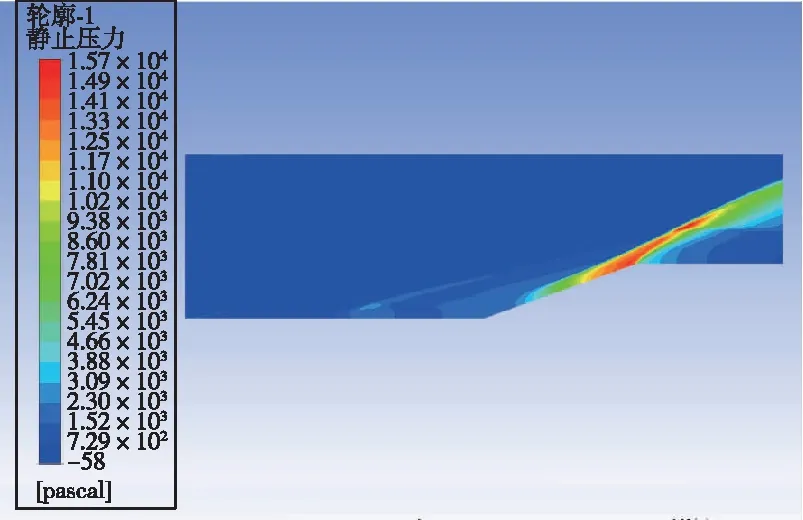
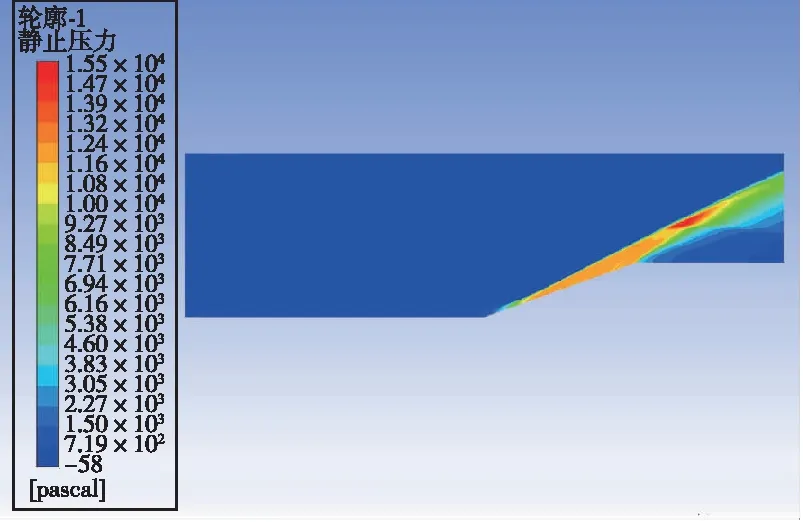
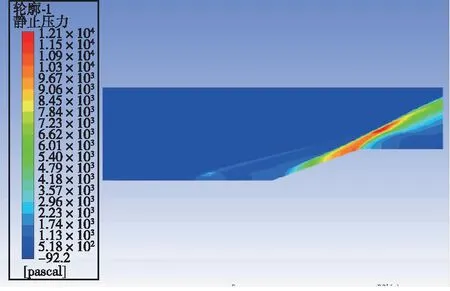
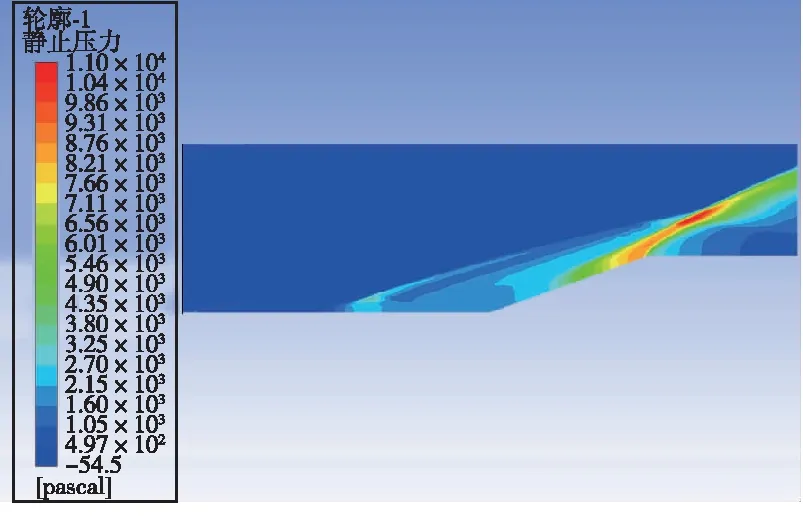
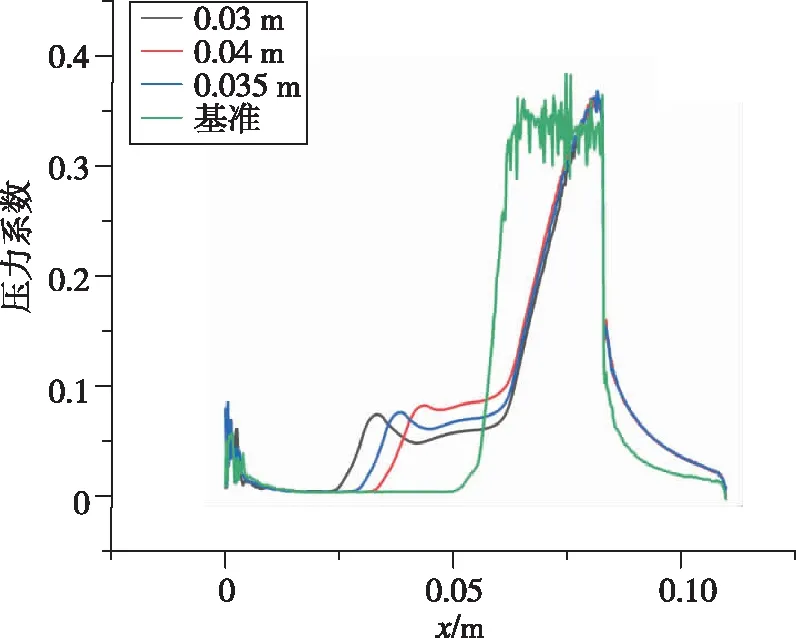
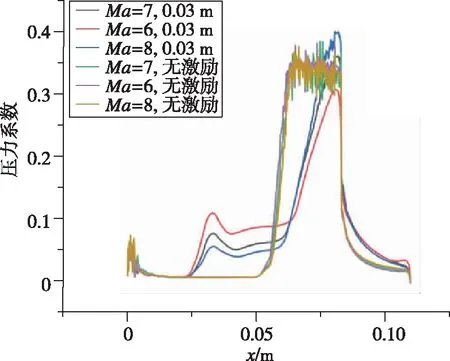
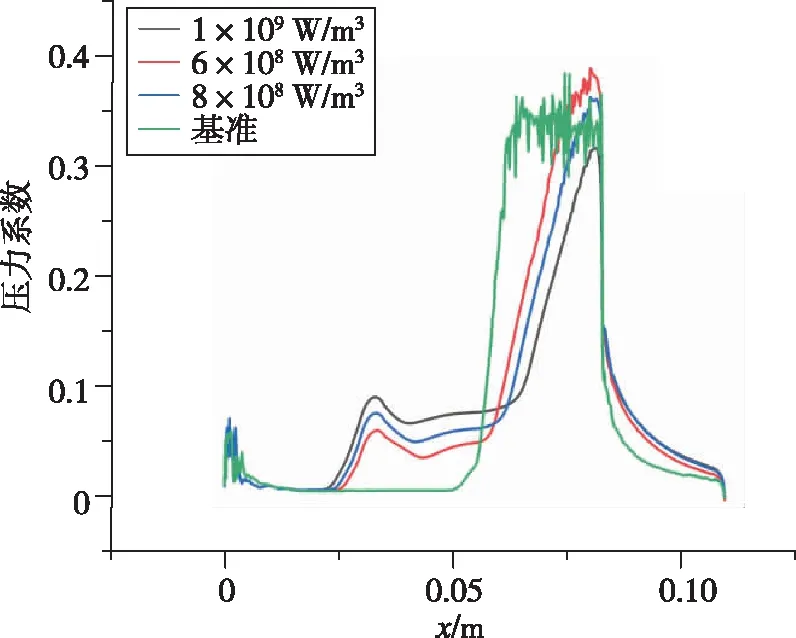
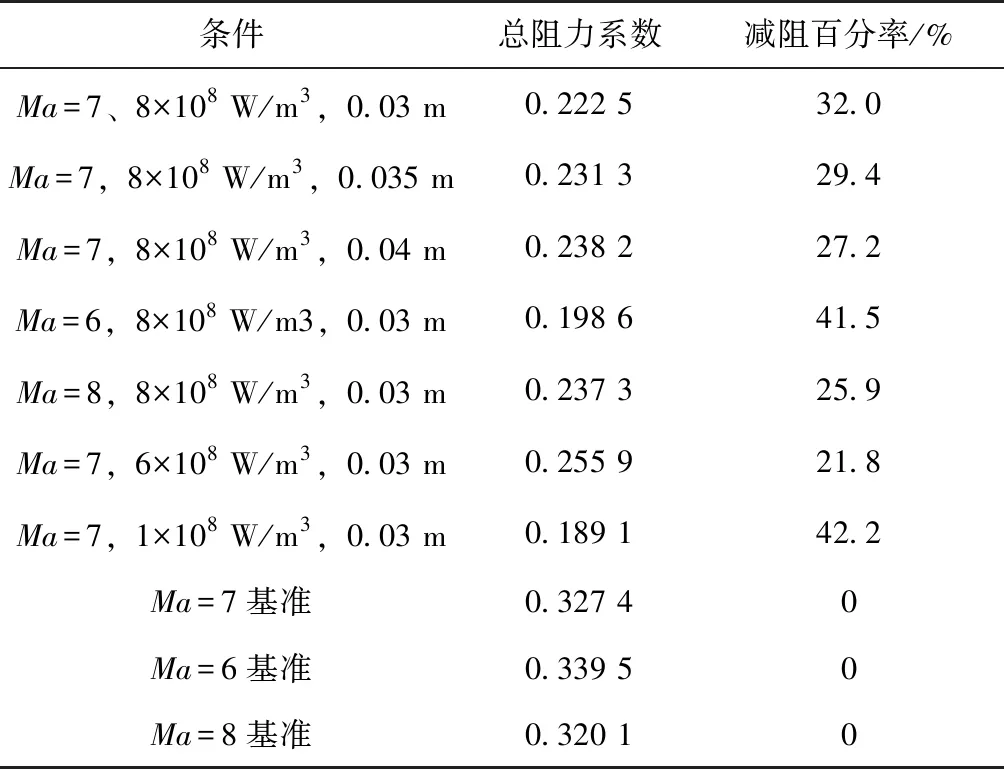
激励以能量源项的方式加入。取阴极表面中轴线上一矩形,坐标为y=5.5 mm,3 mm 数值模拟结果和文献[5]的结果一致。由于文献[5]是三维模拟,这里取的是激励中心平面的二维模拟,因为二维模拟中激励区域沿厚度的每一截面均为二维模型中的激励面积,而实际情况或三维模拟中,由于激励区域是圆柱或椭球,激励区域沿厚度只有中心截面为二维模型中的激励面积,其余截面面积小于二维模型中的激励面积,因此二维模拟中激励区域大于三维模拟中的激励区域,减阻百分率实验的结果大于文献[5]中的结果。 2.3.1 减阻机理分析 没有加入等离子体激励时,高超声速流动经过斜坡尖劈时,产生一道强烈的主斜激波。加入等离子体激励后,高超声速流动和等离子体相互作用,在经过等离子体激励区域时,产生新的斜激波,经过这道激波后,高超声速流动流经斜坡尖劈时再产生主斜激波。这时主斜激波的强度已远远小于没加激励只有一道主斜激波时的强度。高超声速流动通过一系列强度较弱的激波系时产生的流动损失远比通过一道强激波时产生的损失小,产生的激波阻力也是前者小于后者,因此达到减阻的目的。减阻效果的影响要素主要为激励的强度、激励的位置和来流马赫数,下面针对这几个影响因素对减阻效果进行具体分析。 2.3.2 静止压力分布 不同来流马赫数、激励强度和激励位置下静止压力分布如图9所示。可以看出,未加激励时,在斜坡处产生了一道强烈的压缩斜激波,波后压力大大增加,加激励后红色高压区面积大幅减小。图9(a)(b)(c)中,随激励位置的前移,激励后部水平平板上压力增大区域变大,但是区域内压力增大值减小,也就是说,随激励位置前移,激励后水平板上压力变得更分散且值变小。在斜坡上,随激励位置前移,压力图像改变不明显。在来流马赫数恒定的条件下, 激励位置前移表明虚拟尖劈半顶角减小, 根据尖劈斜激波的马赫数-半顶角-激波角三者之间的关系曲线, 可知激波强度减小。图9(g)(h)(a)(d)(e)(f)中,随马赫数减小,激励区域前缘产生的斜激波相对于主激波的强度增强。图9(i)(a)(j)中,随激励强度增大,激励区域前缘产生的斜激波强度增强。 (a) Ma=7,8×108 W/m3,x坐标0.03 m处 (b) Ma=7,8×108 W/m3,x坐标0.035 m处 (c) Ma=7,8×108 W/m3,x坐标0.04 m处 (d) Ma=7,未加激励 (e) Ma=6,8×108 W/m3,x坐标0.03 m处 (f) Ma=6,未加激励 (g) Ma=8, 8×108 W/m3, x坐标0.03 m处 (h) Ma=8,未加激励 (i) Ma=7,6×108 W/m3,x坐标0.03 m处 (j) Ma=7,1×109 W/m3,x坐标0.03 m处 2.3.3 表面压力系数 在激励位置、来流马赫数和激励强度变化下斜坡表面压力系数分布如图10所示。从图10(a)可以看出,斜坡上的压力系数减小了1/3以上,且在斜坡上,似乎激励位置对斜坡的压力系数没多大的影响,而对激励之后斜坡之前的水平板部分,激励后的压力系数比无激励的压力系数大,且随激励位置的前移,压力系数值减小,高压力系数区面积增大,这与前面静止压力分布图里观察到的规律一致。从图10(b)可以看出,随马赫数减小,斜坡上的压力系数减小,激励后水平板上压力系数增大。从图10(c)可以看出,随激励强度增大,斜坡上的压力系数减小,激励后水平板上压力系数增大。 (a) 来流Ma=7、激励强度8×108 W/m3时 压力系数随激励位置变化图 (b) 激励位置0.03 m、激励强度8×108 W/m3时 压力系数随马赫数变化图 (c) 来流Ma=7、激励位置0.03 m时 压力系数随激励强度变化图图10 激励位置、来流马赫数和激励强度变化下 静止压力分布曲线Fig.10 Distribution of static pressure under different excitation positions, inlet Mach number and excitation intensity 2.3.4 总阻力系数 不同来流马赫数、激励强度和激励位置下总阻力系数如表2所示。由表2可见,在来流Ma=7,激励强度8×108W/m3下,减阻最高达32%。在同一马赫数、激励强度下,随激励位置前移,减阻百分率增大。在同一激励位置,激励强度下,随马赫数减小,减阻百分率增大。在同一激励位置,同一马赫数,随激励强度增大,减阻百分率增大。 表2 不同来流马赫数、激励强度和激励位置下总阻力系数 本文设计了一种表面电弧激励器,用于等离子体流动控制,得到了不同工况下表面电弧激励器周围空间温度、电势等的分布情况,获得了激励器准确热源分布。激励器在电流7 A、阴阳极距离3.5 mm时能得到2.690 5×1010W/m3的阴极表面最高热源值,在Ma=7时总阻力系数最多减小32%。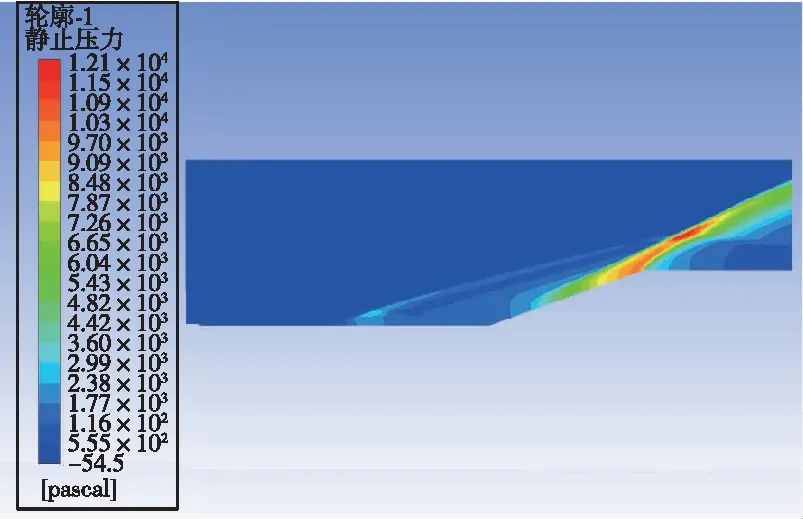
3 结论
