西方形式美理论：核心与演进

张 法

(浙江师范大学 江南文化研究中心，浙江 金华 321004)

提要： 西方形式美理论以黄金比率为核心，在古希腊体现为比例，以方圆中的五角星和黄金矩形为基图，其原理扩展到一切美的方面，其审美境界是静穆的伟大。在近代体现为数列，比例重在空间之形，数列重在时间之动，以无限宇宙为境界，体现为对力的重视和对曲线、自相似的强调，特别以对数螺旋方式突显出来。在现代和后现代体现为分形，分形面对不规则的图形而将之按规则的把握，面对破碎之景象而将之转为可把握的规律，而对从有到无的无限演进把有与无统合起来。比例、数列、分形的核心是黄金比率，黄金比率是西方形式美的核心，比例、数列、分形是黄金比率的三种面相。

形式美理论是把物体为什么是美，不用文化标准而用一种宇宙本质和人类本质相联的理论。虽然形式美的理论也会受到文化的影响，比如中国、西方、印度的形式美理论，就各不相同，但尽管不同，却在从宇宙本身和人性本身去找美之为美这一点上是共同的。本文专论西方文化的形式美理论，笔者以前分别发表过关于西方在三个时代的形式美理论①。这里，进一步将这三个时代关联起来讲，加进一些材料，对内容进行新的提炼，以突出西方形式美理论不同于中国和印度的特点，而且重新指出并强调这一特点，贯穿在整个西方形式美的演进中，这一特点就是：黄金比率(golden ratio)。

以黄金比率为核心的西方形式美理论，经历了三个阶段，首先是古希腊的建立期，以具有哲学本体的logos(比例)体现出来。呈现了希腊之美，强调几何空间的静穆伟大。然后，在文艺复兴开始的近代，以数列的方式体现出来，阐明了与哥白尼天文学和黑格尔的理念相同构的强调时间性的宇宙无限的境界。最后，在19世纪末至20世纪以来科学演进中，体现为分形思想，呈现了一个多元互补的碎片世界，各种现代派美学和后现代派美学，乃至全球互动的多元世界的美学，都与之有关。在分形美学中，西方的形式美理论与中国、印度的形式美学理论，有了更多的契合与会通，成为世界美学重新建构的理论基础。

一、希腊的形式美理论：比例与基形

古希腊的形式美理论与希腊哲学紧密相关。古希腊哲学的本体概念与形式美紧密关联有二：一是作为宇宙整体的Being(有-在-是)，二是作为宇宙运行规律的logos(逻各斯)。宇宙整体的Being(有-在-是)以有规律的logos(逻各斯)方式演化为具体的世间万物，具体之物由这一方式而产生，与规律越近，就越显得美。美的规律对于希腊人来讲，就体现为具体事物具有美的比例。Logos一词，既是具有宇宙规律的“道”的词义，又具有使物成为美的“比例”的词义。Logos就是“比例”。美的比例既普遍地存在于宇宙之中，也存在于人体之中的黄金比率。希腊的示范学科是几何学，在柏拉图的《蒂迈欧篇》中，上帝是几何学家，他用几何形式创造了世界。世界的基本元素，土、水、气、水也成为几何图形，几何美即宇宙的形式美。关于由黄金比率而来的形式美理论，可以从下面三图中呈现出来：

几何学由点成线，由线成面，由面成体，由体而成宇宙万物。宇宙中美的法则，在由点成线上体现为图1：把一条线段分割为两部分a和b，使其中一部分a与全长(a+b)之比等于另一部分b与a之比。这就是黄金比率约等于0.618∶1。宇宙万物中的线，只要按黄金比率呈现就是美的。几何学由线成面，面的基本图形是方、圆、三角。三种图形都内蕴黄金比率于其中，是宇宙万物中的基本图形，各种各样的美的图形都由三者演化而来。但在古希腊形式美理论中，最重要的有两个图形，这就是方圆中的五角星和由正方圆而来的黄金矩形。先看方圆中的五角星(图2)，用圆规直尺准确作出正五边形，正五边形的五条对角线便交织成五角星图案。正五边形的每个顶点，都是黄金分割点，五角星中所有线段的长度关系都由黄金比率构成。五角星的每个角都是36 °(顶角为36 °的等腰三角形叫黄金三角形。其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点)。总之，五角星不但把方圆三角中的黄金比率内蕴在其中，而且本身内蕴着多种多样的黄金比率，五角星是一个充满文化意义的符号。比如，从毕达哥拉斯的数的象征体系来讲，5=3+2，是男性数字(3)和女性数字(2)的结合而代表爱与婚姻。从希腊神话来讲，五角星与希腊健康女神的符号相同而代表健康。从形式美来讲，圆、正方、三角是基本图形，可演化为宇宙中各种各样的图形，其所演化之形，怎样才是美的呢？图3由正方演化出的矩形，这一矩形是按黄金比率形成的，从而是美的。如果说，正方圆三角五角构成的形体，都体现为对称之美和节奏之美，那么，黄金矩形则彰显为均衡和韵律之美。

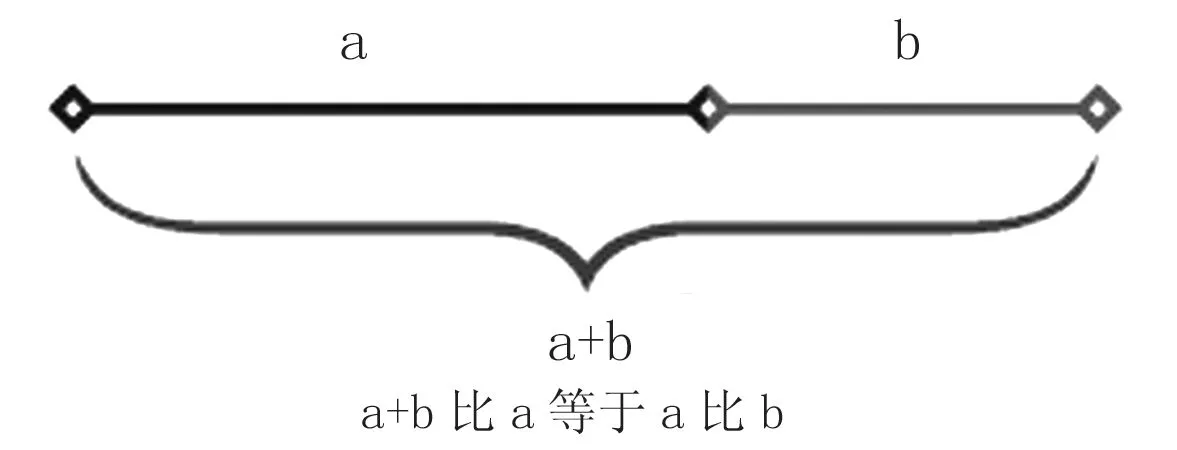
图1 线的黄金比率

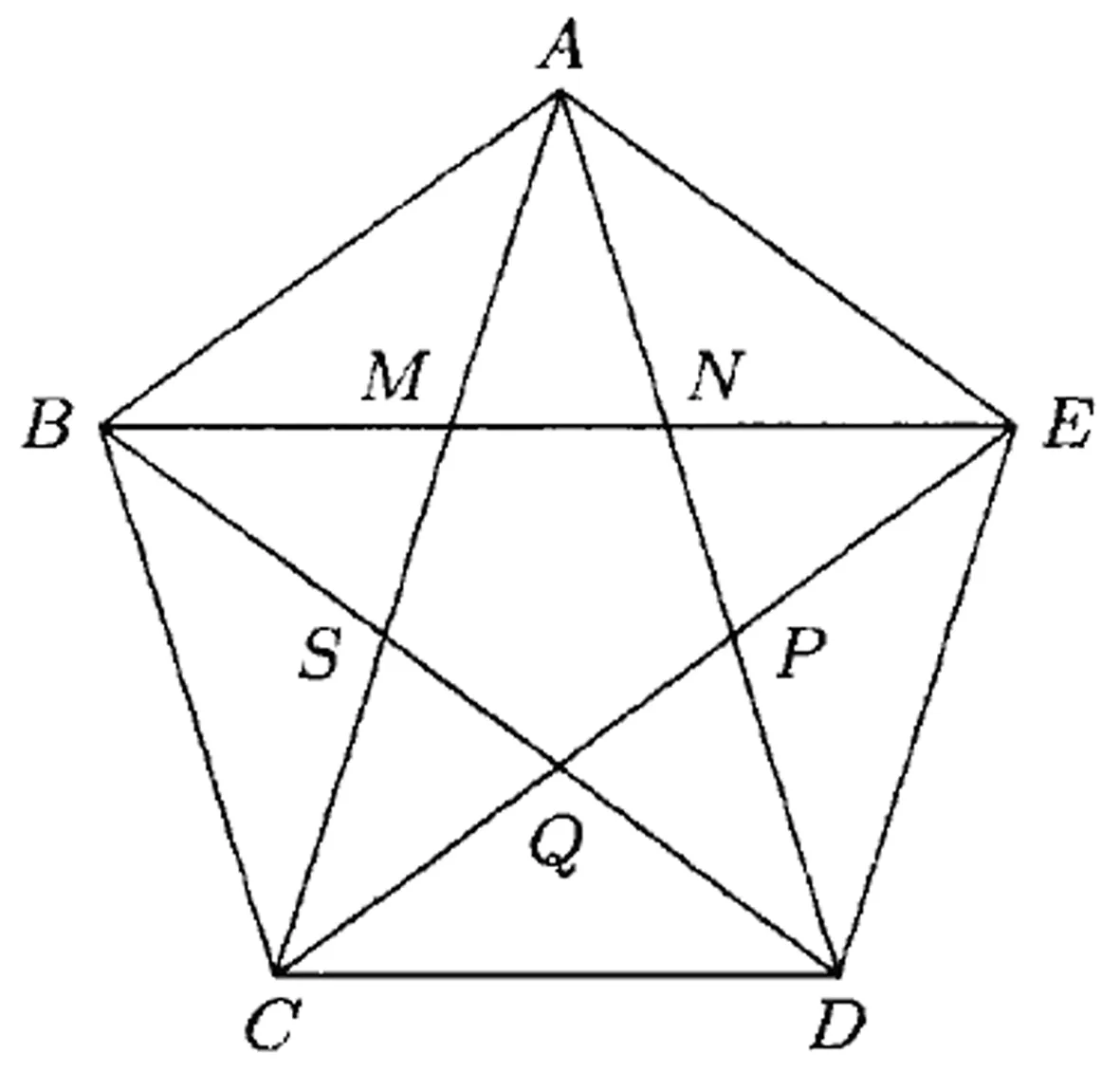
图2A

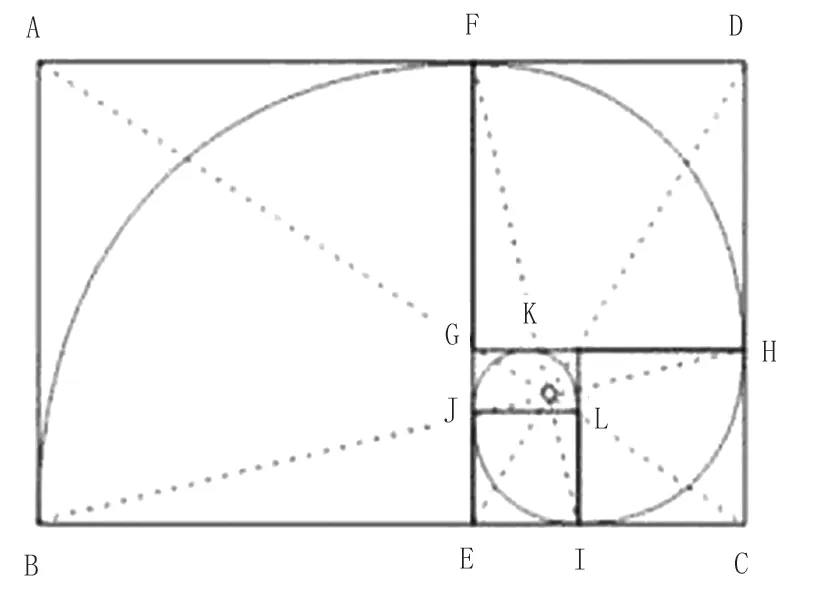
图3 黄金矩形

由此可知，任一图形，只要是按黄金比率构成的，那么它就是美的。在世界文化中，希腊的神以美的人体出现，是因为人体上充满了黄金比率。人体的黄金比，从古希腊理论对《持矛者》的论说，到古罗马维特鲁威《建筑十书》，到文艺复兴时代瓦萨里(Andreas Vesaliua)编《人体结构》(1543年)，再到现代柯布西耶的《数模》，讲了很多，各论特点不同，但都围绕着人体上的黄金比率立论。且以近代的蔡辛(Adolf Zeising，1810—1876年)为例，他将一个人的总高度分成四个主要的区域：头顶到肩膀，肩膀到肚脐，肚脐到膝盖，肚脐到脚底，前三个形成一个递增的黄金分割级数，但是第四个等于第二个。每一个区域又被分成五部分，总共为二十个部分。在每一个区域内，各部分是对称性排列的：要么是ABBBA，要么是BABAB。也就是说，总是2A+3B，比率A：B为1∶Φ。②希腊人讲人是一个小宇宙，正是讲美的人体上充满了宇宙美的形式法则。当西方学人对希腊神像雕塑，如美神、健康女神、睡眠男神，进行形式美分析，要突出的正是在人体中的宇宙美的形式法则。如下：

人体如此，毕达哥拉斯对音乐的分析也是如此，“当琴弦为相同长度时(1∶1)，可以得到同音的效果；当琴弦长度为1∶2时，可以得到八度音程；2∶3时为五度音程；3∶4时为四度音程。换句话说，你可以拨一根弦奏出一个音符，而拨一根一半长度相同紧度的弦，你就会精确地听到一个比它高八度的音。同理，C调音符的6/5是A调，它的4/3是G调，3/2是F调，等等。”[1]32同样，星空中各星体运行的和谐是由各星体之的距离之线构成的，“从地球到月亮是一个全音程；从月亮到水星是一个半音程；从水星到金星是另一个半音程；从金星到太阳是一个小调三度音阶，等于三个半音程；太阳到火星是一个全音程；火星到木星是一个半音程；木星到土星是一个半音程；而从土星到固定的星体是另一个小调三度音。”[2]36在毕达哥拉斯看来，宇宙是一个琴弦的位置上带着水晶琴的巨大竖琴。后来佛拉德(Bobert Fludd)在自己的《大宇宙历史》第一卷中，以神圣单弦琴的形象来总结其宇宙学：“一个包含两个八度音阶的毕达拉斯的和音被分为全部的基本和谐音程，每一音程描述一个宇宙因素。流程从低G开始，这是地球，上升到C，在这一点上上帝在这里露面，又从这上升到高G，这是上天的最高处。整个和音的两个八度音阶代表了宇宙的和谐：‘宇宙的音乐’。”[2]122整个宇宙万事万物都是由黄金比率而显现出美来。因此，对于古希腊人来讲，要发现美和创造美，只要按照这一比率法则去找出符合黄金率的线、面、体、形就可以了。理解了这一法则，就可以理解希腊的建筑、雕塑、戏剧，为何用这样一种形式呈现自己的美。从现象上看，希腊由几何学而来的比例之美，是静态之美，这是一种类似于哲学家芝诺讲的“飞矢不动”之静，是个体的，但又内蕴了宇宙的精神。温克尔曼把希腊艺术称为：静穆的伟大。但黄金比率不仅是静止的，这从上图2B可以看到。五角星之中又是一个五边形，五边形中又可成一个五角星，如此循环，一个比一个小，趋向微观世界的无限。同样，这个五角星也可以同形扩大，一个比一个大，趋向宏观世界的无限。再看图3，矩形ABCD之长边中黄金分割点作线FE，形成一个正方形和一个矩形。黄金矩形也与五角星一样，可以向大的或向小的同扩大或缩小。在小矩形之长的黄金分割点上作线GH，形成一个更小的正方形和一个更小的矩形，在这一小矩形上做同样的分割，如此循环，一个比一个小，趋向微观的无限，也可一个比一个扩大，趋向无限。方圆中的五角形和黄金矩形这两个古希腊的基本图形，透出了黄金比率本有着动的内容，只是被转化为静的形态。这一以静态为主的比例，自古希腊以来，从近代到现代到后现代，都在不断地被完善，形成西方形式美的重要内容。但黄金比率的另一方面，动态方面，在近代的思想演进中，突显了出来，并产生了形式美的新法则。

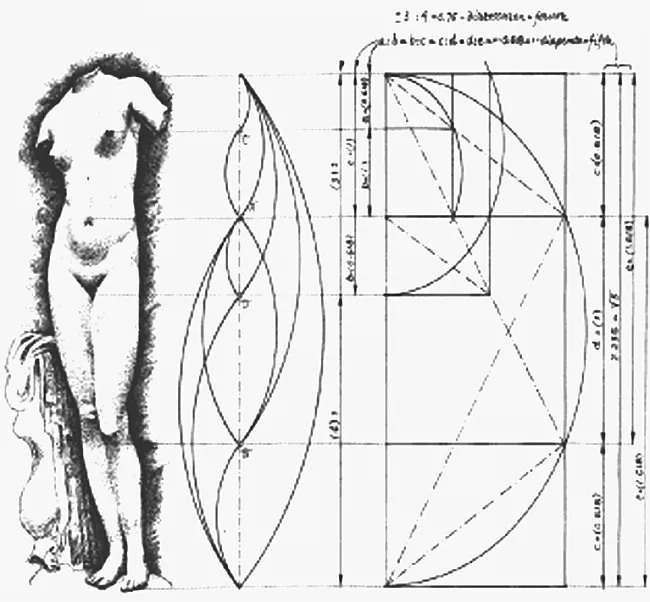
图4 阿芙洛蒂特身体的黄金比

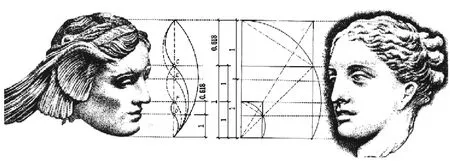
图5 睡眠男神和健康女神面部的黄金比

二、近代的形式美理论：数列为主的形式美。

文艺复兴、宗教改革、科学革命、启蒙运动，掀开了西方历史的新篇，以黄金比率为核心的形式美理论，从以比例为主转到以数列为主。斐波纳契(Leonardo Fibonacci，1175—1250年)在《计算之书》(1202年)里用一个故事提出了数列问题：第一个月有一对兔子诞生，第二个月之后它们可以生育，每月每对可生育的兔子会生下一对兔子，如果兔子永不死去，且时间一直无穷向前。从最初开始以后一月一月地依次数下去，每月(原有的加上新出生的)有多少对兔子？这一答案形成如下数列：

1，1，2，3，5，8，13，21，34，55，89，144，233，377，610，987……

这个数列从第三项开始，每一项都等于前两项之和(1+2=3，2+3=5，2+5=8……)无论这一数列怎样向前演进，这一规律始终不变。这彰显出一种承继着古希腊理性而来的近代理性。作为形式美来说，更为重要的是，这一数列中的每两个连续数字之比，在波动中，越来越趋向黄金比率[1]116。近代的斐波纳契数列与古代的欧几里德几何在表现黄金分割这一内容时是相同的，且可互换，但是当黄金分割以几何图形显示出来时，呈现为一眼即可以把握的整体，当以数列呈现出来时，成为永无穷尽的无限演进。以几何还是以数列的方式呈现黄金比率，突出的重点和给人的感受是不同的，呈现的内容和精神是不同的，前者是古代的，后者是近代的。古代突出的是静态，近代强调的是动态，黄金比率是无理数，当时令毕达哥拉斯非常惶恐，下了保密的封口令，实际上几何方式本就使无理数显不出来，近代用数列把无理数外显出来。正如哥白尼的日星说开始了一个无限的宇宙。具有空间特征的几何比例转成具有时间性的斐氏数列，本就内蕴在几何比例中的三大原则被突显出来：力的发现，曲线之美，自相似原则。按黄金比率演进的数例呈现(向前)增加和(向后)减少的动态，在古代的五角星和黄金矩形中，已经看到了这一扩大和缩小的动态，但在这两种形状中，动态是具体的，是五星和矩形的动态。数例的动态则是抽象的，可以体现在任何现象上，比如在天文学上，近代天文学在与前面谈的莱弗拉德的带着神秘性的天文学不同的是由哥白尼、开普勒、牛顿代表的另一路向。特别是开普勒的理论，呈现了前两个原则。开普勒关于星体一日间运动中形成天体的比例理论。即对于一个太阳的观察者来说，将显现为在24小时的时间内的近日点和远日点运行的路线的弧的基础之上的。例如，如果从太阳上看，当土星接近太阳的时候每天运行一个135秒的弧线。在它离太阳最远时，对于一个太阳观察者来说行星好像运行了一个106秒的弧线。135与106的比例是5：4，从天体的音乐性上讲，这正是大三音程(虽然这里有微小差别。它实际上是5∶3.9259的比例，但差别在大多数的耳朵和大多数智者的头脑中可以忽略)。用这种方法，开普勒发现全部六个行星都产生了几乎都精确地可以用完美的多角形表现的和谐的比例。P木星的近日点/远日点的比例近乎是6：5，小三度音；火星的比例是3：2，五度音；地球的比例是16：15，半音符；金星的比例是14：25，正好等于毕达哥拉斯学派的小音程；而水星的比例是12：5，一个八度音阶和一个小三度音[2]143。这里，天体音乐的形式美比例显出了两大特征，一是比例具有动态的特点，二是运动的轨迹突出了弧线。区别于亚里士多德和托勒密的正圆，这里应合了数列另外一个非常重要的特征：对曲线的突出。开普勒沿着自己的方向前进，发现了行星运动的三大定律。牛顿则在开普勒天文学的基础，发现了决定行星运动何以如此进行的万有引力。可以说，近代天体音乐的演进，对于形式美来说，突出了两个东西：一是曲线，一是引力。前者把形式美从形体的静态转变到生长的动态，后者把形式美从外显可见的“形式”引入到内隐可感可计算的“力”。力在近代还没有进入到美学领域，在现代现象艺术出现以后，方在一系列理论体现出来。曲线从数列中突显出来，当斐氏数列不按1、2、3、4、5、6……的自然数列演进，而按黄金比率进行演进，本就具有曲线精神。将黄金比率运行的数列曲线运用于宇宙的广大领域，发现了对数螺旋。几何图形中本就内蕴着的对数螺旋也彰显出来。在黄金矩形中，如果将这些“旋转直角”按照黄金比例划分边长的点连接，就能得到一条内旋的对数螺旋(见图3)。同样，在黄金三角形(即一种等腰三角形，边与底的比是黄金比)里，将其底角平分，你就得到了一个小的黄金三角形。不停地把底角平分，就会造出一系列旋转的三角形，这一系列黄金三角形的顶点相连就画出一条对数螺旋。不从数学的角度而从几何的角度去看，对数螺旋就成了对角螺旋(笛卡尔就是从几何的角度得出了这一名称)。从极点任意画一条直线到曲线上的一点，它完全按相同的角度分割曲线。对数螺旋形成的曲线不仅仅是在几何图形中，而普遍存在于植物生长之中、动物行动之中、天体演化之中。且以植物为例，在植物的花中，最常见的花瓣数目是5枚(如蔷薇科的桃、李、杏、苹果、梨)，其他常见为有3(如鸢尾花、百合花，此花看去6枚，实为是两轮3枚);有8(如飞燕草);有13(如瓜叶菊)；一些植物的花瓣有多形，向日葵有21和34两型，雏菊有34，55，89三型。这些数：3、5、8、13、21、34、55、89，正好是费氏数字。最重要的不仅是这些数字的与费氏数字相合，而是由这些数目的花瓣形成了对数螺旋的形态，且往往是两组对数螺线，一组为顺时针方向，另一组为逆时针方向，如花菜、菠萝、松果、向日葵……植物之呈现对数螺旋，正是要通过静态的形态显出动态的生成，这体现在植物的叶序上。“叶序是指叶子在茎上的排列方式，最常见的是互生叶序，即在每个节上只生1叶，交互而生。任意取一片叶子作为起点，向上用线连接各片叶子的着生点，可以发现这是一条螺旋线，盘旋而上，直到上方另一片叶子的着生点恰好与起点叶的着生点重合，作为终点。从起点到终点之间的螺旋线的绕茎周数，称为叶序周。不同种植物的叶序周可能不同，之间的叶数也可能不同，例如榆，叶序周为1(即绕茎1周)，有2叶；桑，叶序周为1，有3叶；桃，叶序周为2，有5叶；梨，叶序周为3，有8叶；杏，叶序周为5，有13叶；松，叶序周为8，有21叶……但以其绕茎的周数为分子，叶数为分母，可表示为：1/2，1/3，2/5，3/8，5/13，8/21……它们全都是由斐波纳契数组成的。这些是最常见的叶序公式，据估计大约有90%植物属于这类叶序。”[3]叶序为什么呈现对数螺旋形态呢？“对于许多植物来说，每片叶子从中轴附近生长出来，为了在生长过程中一直都能最佳地利用空间(要考虑到叶子是一片一片逐渐地生长出来，而不是一下子同时出现的)，每片叶子和前一片叶子之间的角度应该是222.5度，这个角度称为‘黄金角度’，因为它和整个圆周360度之比是黄金分割数0.618033989……的倒数，而这种生长方式就决定了斐波纳契螺旋的产生。”③“事实证明利用费氏级数角度进行新陈代谢的叶子获得了最小的重叠和最大的暴露。”[4]在动物里，不少贝类，如鹦鹉螺、望远镜螺，有对数螺旋，动物双角、人体的耳蜗，都显出对数螺旋；更有趣的是，猎鹰扑向猎物和飞蛾扑火，都是按照对数螺旋的轨迹俯冲而下的。当我们用哈勃望远镜对拥百亿计太阳恒星鸟宇宙进行观测时，在所能观测到的大约万亿个星系中，许多都是螺旋星系。“为什么如此众多的星系显示出螺旋形状呢？螺旋星系就如同我们的银河系，有一个相对较薄的银盘(就像薄烤饼)，由气体、灰尘(细微颗粒)和星星组成。整个银河系的银盘围绕银河系中心旋转。例如，在太阳周围，绕银河中心旋转的轨道速度是140英里/秒，完成一圈需要大约2.25亿年。离中心距离不同，速度也不同——近的快，远的慢——也就是说，银河系的银盘并不是整块旋转，而是分别以不同的速度运动。从正面看，螺旋星系在中心近旁生成螺旋臂，外围穿过星云向外扩散。螺旋臂是银河系银盘的一部分，在那里孕育着许多新星。因为新星是最亮的，所以我们能从远处看到其他星系的螺旋结构。天文学家们要回答的基本问题是：螺旋臂的形状如何能长时间保持不变？因为银盘内部比外围的旋转速度要快，任何与银盘物质有关的大规模形体都不能长久存在。同我们的观察相反，一个由相同星体和气体集合产生的螺旋结构会不可避免地产生纠结。螺旋臂能长久存在的原因要归于密度波——穿过银河系银盘的气体压缩波——沿路压挤气体所引发新星的形成。我们看到的螺旋图案仅仅是银盘中密度大于一般的部分和新生星。所以，这个图案重复出现，没有产生纠结……使星体和气云转动偏移形成螺旋密度波的原因(就银河系里的物质分布不对称所产生的引力)。举例来说，在一系列围绕中心的椭圆轨道里，每个轨道和中心的距离有稍微的偏转，就形成了一个螺旋图案(事实上，我们应该为现在宇宙里引力的作用方式感到高兴)。根据牛顿的重力理论，每个物体都会吸引另一个物体，相互间的引力随距离增加而减少。牛顿运动定律显示，由于距离决定引力，围绕太阳的行星轨迹就呈现椭圆形。如果我们居住的宇宙引力是以8倍引力对2倍距离的方式减少(引力随距离的立方减少)，你可以想象一下，这个世界会发生什么情况，在那样一个宇宙里，牛顿定律预示，可能的一种轨迹会是对数螺旋。”[1]139-149要解释鹰和蛾的飞行动态，与其视角器官与目标物互动相关，要解释植物生成的对数螺旋，与植物与环境的互动相连，要解释星空中的螺旋星云，则与太空中的力相关。这里万有引力之力再一次显出了自己的存在。但对于整个近代的形式美来说，对数螺旋突出的还是曲线主题。古希腊的美学家异口同声地说，圆是最美的，强调的是圆由直线而来。近代美学家贺伽兹(William Hogartu)却说：蛇形线是最美的，这里让人感到对数螺旋被突显出来的时代氛围。如果对数螺旋与各文化从原始时代就开始，如中国远古的旋目等结合起来，与中国的太极曲线相比较，世界形式美的规律会得到进一步呈现。

图6 植物的对数螺旋

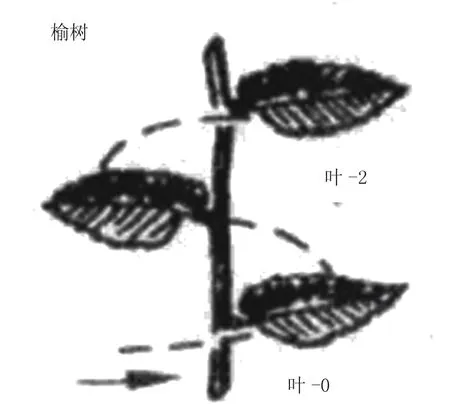
图7 植物生长螺旋

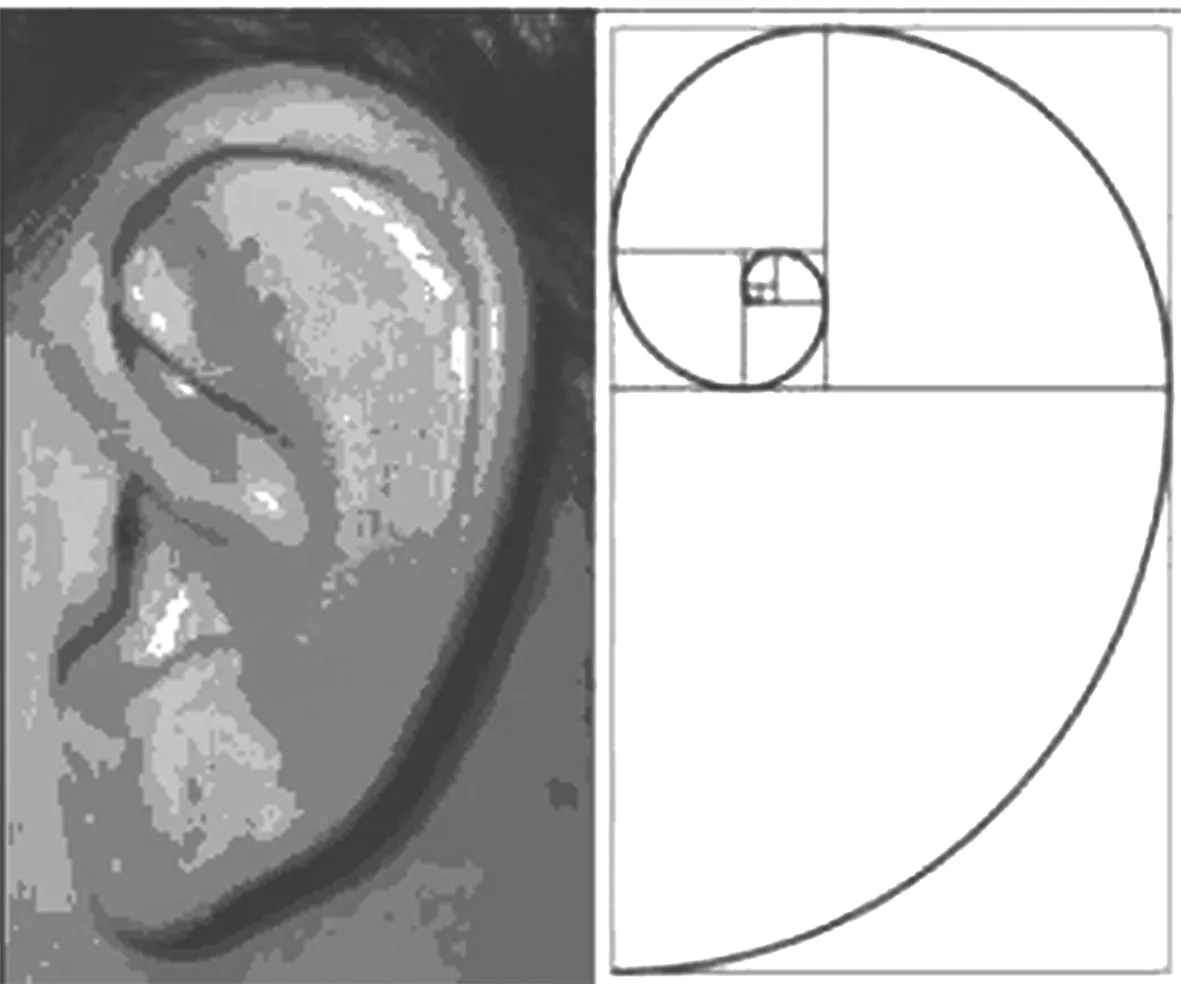
图8 人体对数螺旋

图9 天文对数螺旋

对数螺旋同时又体现了数列突显出的第三个特点：自相似，自相似本就内蕴在五角星和黄金矩形中，五角形和黄金矩形不断扩大和不断缩小，都是一个个更大或更小的五角星和矩形按自相似的方式出现。而对数螺旋体现在各种物体上，如植物之树叶、螺虫的外形，星体的样态，反映的是物体实体体征上的自相似，当体现为运动之时，是螺旋抽象线条的自相似。由黄金比率而来的自相似体现在对数螺旋上。因此，对数螺旋包含了两大内容，一是曲线，二是自相似。对数螺旋把自相似突显出来，之后现代的分形让自相似形成了一个更为普遍的原则。当数列突出了形式美中的力、曲线、自相似三大新特点之后，黄金比率的进一步演进在分形几何的形式美凸显。

三、现代和后现代的形式美理论：分形与多元互动

在第一点上，分形理论提出了“特征尺度”概念。宇宙是多种多样的。要测量客观世界中的事物，根据事物大小轻重实体的特征不同，测量的尺度工具也会不同，用尺去测万里长城嫌太短，量大肠杆菌又太长。因此合适的“特征长度”显得重要。但有的事物没有特征尺度，如天上的白云、河中的湍流、室内的轻烟……是不断变幻着的(用术语讲是“无标度性”的)，怎么去测定呢？可知比例和数列作为一种特征尺度，仅与一部分的物体相适合，而与之不适应的物体，则无能为力。而且有些事物，表面上看起来是适宜，实际上还只是适宜的尺度之一，并不一定能完全反映所观察和测量的物体，以曼德勃罗提出分形时的实例：测定英国海岸线有多长。海岸线的长度事实上取决于所用尺子的刻度。假设用的是英国的卫星地图，其边长有一英尺，量出长度，然后再乘以已知的地图比例尺，把它转化成实际长度。显然，这种方法会忽略海岸上实际存在不规则的弯弯角角。如想要更精确，可带上一码长的棍子，沿着英国海滩而行，艰难地一码码地度量。得到的数字会比上一次大得多，因为那些较小的弯角都被计算在内了。但是，这仍然忽略了长度小于一码的地方。只要每减小一次尺子的刻度，长度就会有更大的值，因为每次都能发现那些更小的分结构。因此，测量现实中的不规则形状时，作为尺度的长度概念也需要更改。海岸线并不能如同想象的那样变成直线，而是在各个规模大小上都有弯曲，而且长度会无限地增加(至少直到以原子为刻度)[1]252-253。观察海岸线，可用比例方式去看，数列方式去看，也可用分形方式去看，不同方式得出的无论是科学的还是美学的，都是不同的。海岸线呈现为怎样的数字和怎样的景观，是与观测的方式相关联的。可以说，比例、数列、分形是三种不同的审美方式，面对同一对象，得到的是三种不同的审美感受。因此，由分形而来的形式美理论，不仅可以理解西方形式美的(比例、数列、分形)三种模式的不同，而且还可以体悟西方形式美与其他文化的形式美的差异。

从分形几何的特征尺度而得出的结论：世界呈现为什么这样，是与人的看的方式紧密联系，这一思想还体现在非欧几何上，这一新说从罗巴切夫斯基(Николáй Ивáнович Лобачéвский，1792—1856)、高斯(Johann Carl Friedrich Gauss，1777—1855)到黎曼(Georg Friedrich Bernhard Rieman，1826—1866)的演进。基本思想是在对欧氏几何的第五公理，给出相反的结论，并在此基础上，形成一套自足的几何体系。从欧氏第五公理讲，从平行线外一点，只能引出一条直线与已知直线平行。罗巴切夫斯基讲，从平行线外一点，可以引出一条以上的直线，与已知直线平行。黎曼讲，从平行线外一点，连一条与已知直线平行的直线也画不出来。从欧氏几何的第五公理出发，非欧几何得出了一系列与欧氏几何不同的结论，比如三角形的内角和，不是大于180°，就是小于180°等。非欧几何与欧氏几何的差异，在于欧氏几何是平面上的几何，非欧几何是曲面上的几何。如图：

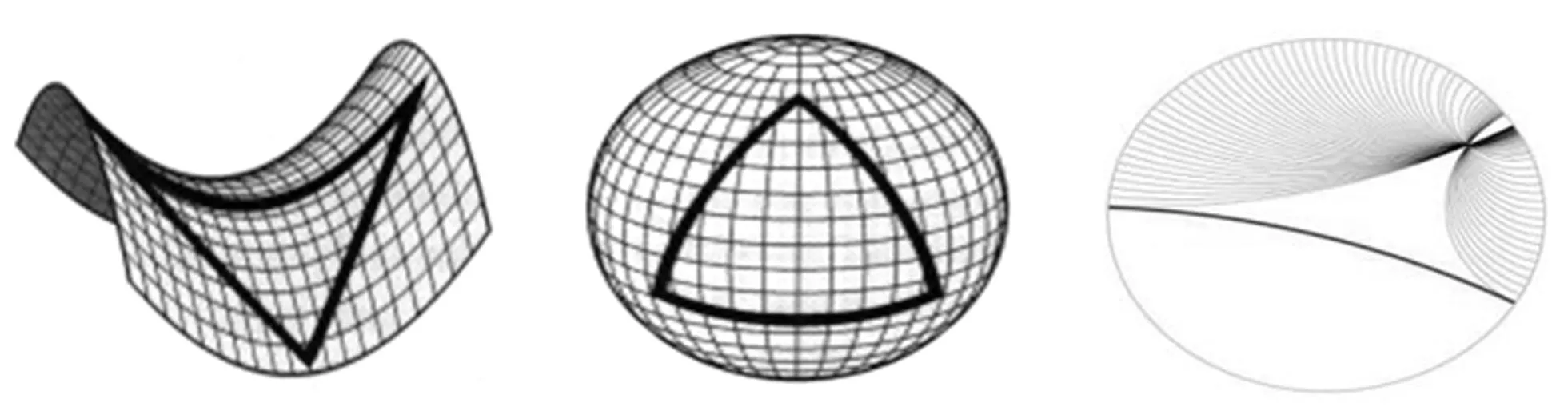
图10A 三种曲面几何中的三角形

图10B 曲面中的圆

非欧几何与欧氏几何在一些定理上完全相反，而相反的两者又都是对的，这主要在于二者要看的东西和看的方式是不同的。地球本来不平，但欧氏几何要将之抽象为平面来进行理解，非欧几何要按照地球本来的曲面进行抽象。这两种不同的理论，会产生不同的世界感受的景观，这体现在埃舍尔(Maurits Cornelis Escher，1898—1972)的画中。非欧几何虽然由不同于欧氏几何的第五公理产生出来，但在其他四条公理上又与欧氏几何相同。这两个相反的理论又有相同的一面，也反映在埃舍尔的画中：

图11一些人向上走，一些人向下走，但结果还是在一个平面上。图12本是平流的水，结果却高出许多，这些确是矛盾之处，又确逻辑地体现在一幅图中。图13两只手都在画，分不清哪只是作画的手，哪只是被画出的手。非欧几何带给人们的观念，还可以在很多现代派绘画中得到体会。非欧几何与分形几何在世界与主体的关联上相同，对于美学来讲，分形几何有更值得重视的特点。

图11 埃舍尔画中人的上与下

图12 埃舍尔画中水的高与低

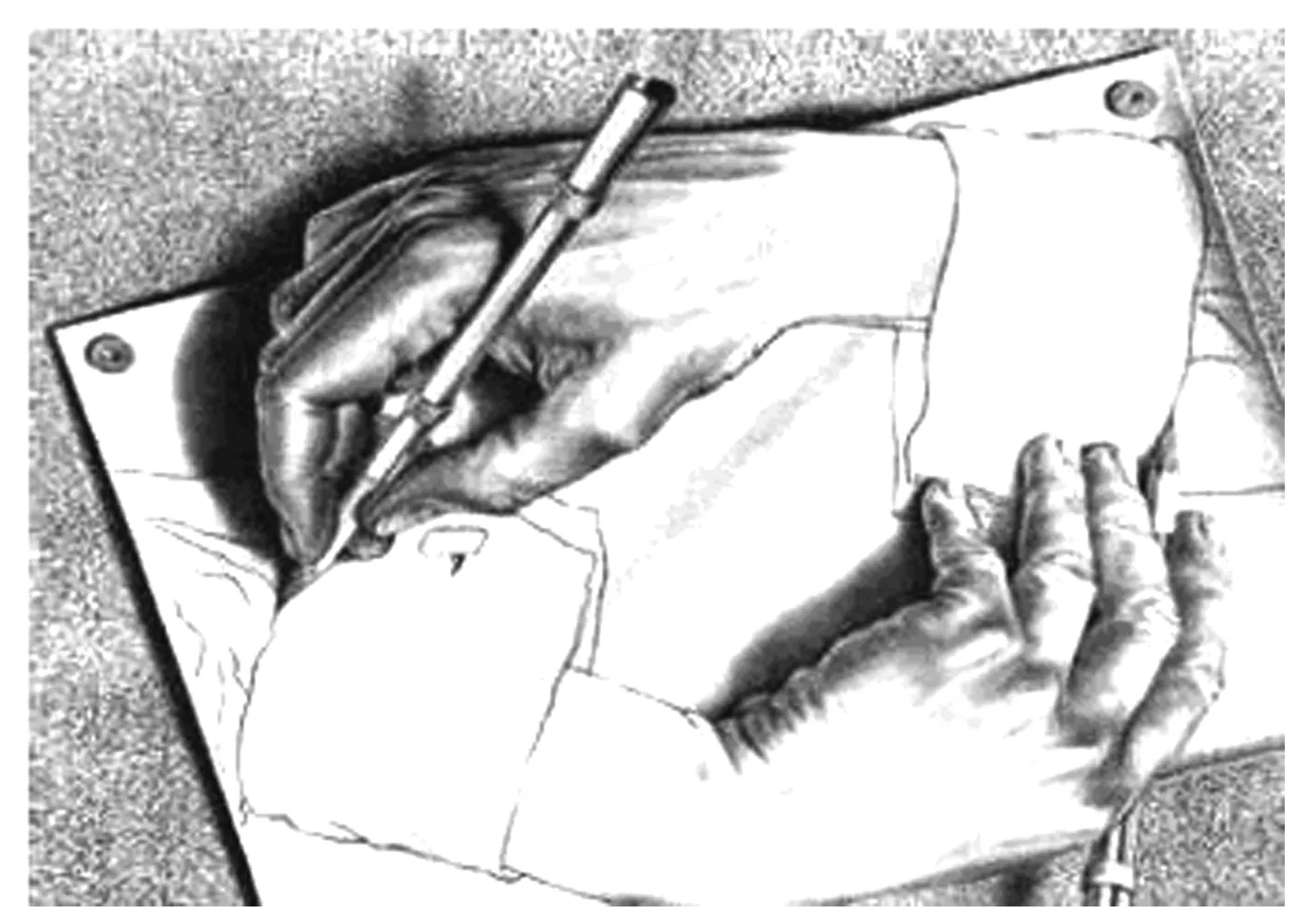
图13 埃舍尔画中手的互画

分形理论的第二点，就是要面对不规则的、皱褶的、破碎的形状。如面对海岸线这样可以用比例和数列去看的对象，用分形去看，突出的正是比例和数列所看不了的而恰是用分形可以看出来的那一方面，但更重要的是一些不能用比例和数列去做，而只能用分形去看的物类：天上的白云、河中的湍流、室内的轻烟……从这里可知，分形对于比例和数列是一个根本性转变。比例和数例，都是要把复杂的现象，抽象为规则的图形和节奏、均衡和韵律。而分形，则面对的是比例和数列在抽象中被简化了的东西。从学科上来讲，在古典几何中，所有物体的维数都只用整数表示，点是零维，线是1维，面是2维，体是3维，而分形几何则是分数维。如平面形的科赫曲线的维度在0与1之前，是个分数，立体形的门杰海绵⑤的维度在1与2之前，是个分数。分数维度正是为更精确地测量有皱褶不规则的事物而产生出来。它让抽象的规整的几何进入了不规则的现实之中。并让这不规则显示出规则来，让破碎被法则所把握，古典几何让我们把握规则之形和整体之形，从而领会规则美和整体美后面的法则，分形几何让我们理解不规则、皱褶、破碎之形，体悟不规则、皱褶、破碎之美后面的要义。这一原理，从柯赫为把握雪花而形成的曲线透露出来。该曲线的生成过程如图：

图14 柯赫雪花的生成图

首先，画一个正三角形，边长为1英寸，然后在每边的中间构建一个更小的三角形，其边长是1/3英寸，这样，得到第二个图形(一个以色列的象征符号：六角星形)。三角形的原始边长是3英寸，而现在它由12个部分组成，每个都是1/3英寸长，所以现在它的总周长是4英寸。以后连续地重复此操作，即在三角形的每一边上构建另一个三角形，其边长是前一个三角形的1/3。每增画一次，其周长会增加4/3倍，直到无穷，尽管事实上它所在的仍是一个有限的区域，但是我们可以展示，这个有限区域是原始三角形的8/5倍[1]253-254。科赫曲线与费氏数列一样，是趋向无限的。科赫曲线显示了三个特征：第一，是自相似的增长演进。但自相似与比例中的五角星和黄金矩形的自相似不同，不是向内的(在已知之中的)，而是向外的(进入未知的)。第二，这一自相似是从规则走向不规则，从舒展走向皱褶，从整齐走向破碎。第三，其演进既是四面前向，又是越来越小，最后趋向“无”。科赫曲线与裴氏数列一样，是向前增长，趋向无限，但裴氏数列的直线向前增长趋向的是一元论和总体性的带着Being(有)的特征“无限”，而科赫曲线的四面向前越多越小的演进，趋向的是后现代的多元论和不通约的No-Being(无)的“无限”。这也是分形理论的分数维与古典几何的整数维对照之后而来的效果。画一根直线，如果用0维的点来量它，其结果为无穷大，因为直线中包含无穷多个点；如果用一块平面来量它，其结果是0，因为直线中不包含平面。在科赫曲线中，它的多元视点和不通约性是在与费氏数列一样的生成演化的动态中呈现的。科赫曲线在生成演化中与费氏数列的不同在于：曲线的任何处不可导，即任何地点都不平滑，走向破碎，在破碎中呈现由古典几何不能把握而分形理论可以把握的规律。这是已经透出了分形理论的第三特征，分形的演进消失在“无”中。在宇宙的无规则、皱褶、破碎的物象中，分形的增长或生长在全方位的演进中愈多又愈小，最后趋向于无。且以树木为例。树木的生长，主要特点就是分枝。从分形模型来说，先找出单位长的枝干，成120度分成两枝，长度为原长度的1/2，每枝再按照同样方式继续往下分，如此反复。如果长度简缩因数不是1/2，选大一些的数，比如0.6，这样分枝之间的空间就会减少，直到最后分枝重叠。对许多系统来说，比如排水系统或血液循环系统。如果要问究竟在简缩因数为多少时，那些分枝刚好接触到对方，开始重叠，研究的结果是：刚好在简缩因数恰好大于黄金比例1/Φ=0.618……时，会发生这种情况。因此这样的图形被称为黄金树，从分形理论的角度看，其分数维大约是1.4404。其实分形还在继续，只是已经小到看不见，是在一个无之中进行，类似于已经转成了中国思想中的气。

图15 树木分形图

分形毕竟是理论学科，虽然对应着宇宙中的相关物象，但它有自身的理论体系。从理论上讲，不规则碎片之形不仅可以由线段组成，而且也能由简单的平面图形，如三角形和正方形组成。三角形就是前面讲过的科赫曲线。这里需要补充的是，三角形愈多愈小之后，简缩因数为多少时，三个大的主枝开始接触，答案同样是：1/Φ=0.618。再用正方形来建造相似的不规则碎片形，同样的情形就会发生：当简缩因数是l/Φ=0.618时，重叠开始[1]256-258。这意味着什么呢？由黄金比率决定的分形呈现的这样的物象，走向破碎，最后到视之不得其形，听之不闻其声，嗅之不觉其味，但又确实存在着的虚体之无的状态中。分形几何的特征，同样可以在埃舍尔的绘画中得到体现。下面图16的A和B两幅图是由曲面而来的分形图，图16C不但是分形的一种，而且有死物与活物的相互转换，艺术之鱼与现实之鱼的相互转换，还有黑白虚实的相互转换。

图16A

分形内蕴着黄金比率，透出了从古典几何到费氏数列再到分形理论，有一种内在规律耦合其中，而古典几何、费氏数列、分形理论，只是这一规律的三种不同的方面。而这种三不同方面，构成了世界种种事物之为美的内在基础。

注 释：

①张法：《以比例为核心的古希腊形式美》，《西北大学学报》2013年第5期，《以数列为核心的近代形式美》，《社会科学战线》2012年第4期，《当代形式美的几个主题》，《中山大学学报》2012年第5期。

②以上从“蔡辛将一人……”到“最小部分”，引自【英】理查德·帕多万：《比例——科学·哲学·数学》，周玉鹏、刘耀辉译，申祖烈校，中国建筑工业出版社，2005年版，第310页，但因文意作了一些调整。

③网上百度百科“斐波纳契数列”，http：//baike.baidu.com/view/1074762.htm.

④曼氏自道云，这一关键词是他在1975年夏天的寂静之夜偶翻拉丁文字典时灵感一闪得到的。曼氏一直在用英文fractional一词来表示他的分形思想，这时他看到了拉丁文形容词fractus(破碎)和动词frangere(产生无规破碎)，而英语的fraction(“碎片”“分数”)及fragment(“碎片”)都来自同一拉丁词根，于是他取拉丁文之头和英文之尾，形成了这一具有重要意义的fractal一词。曼氏1967年，发表《英国的海岸线有多长》，开始分形思想；1975年，发表专著《分形：形状、机遇和维数》创建分形几何学。1982年出版了《大自然的分形几何学》，成了分形的经典著作。

⑤奥地利数学家门杰(Karl Menger，1902—1985)从三维的单位立方体出发，构造了门杰“海绵”：取一立方体，第一步把立方体27等分后，舍去体心的一个小立方体和六个面面心的小立方体，保留20个小立方体。第二步再对20个小立方体作同样处理，此时保留下来的小立方体的数目为20×20=400个。如此操作，直至无穷。于是在极限情况下其体积趋于零，而表面积趋于无穷大，所以实际上得到一个面集。