广义-Mycielski图的集合点色数

贾泽乐, 李沐春

(兰州交通大学 应用数学研究所， 甘肃 兰州 730070)

0 引 言

图染色是图论中的重要方向之一,在组合分析和实际生活中有着广泛的应用.1952 年,Dirac[1]和Youngs[2]通过四色问题的研究提出了图G的点染色概念,并把所用颜色的最小数称为点色数,记作(G).1973年,Bondy等[3]证明了不包含奇圈和完全图的简单连通图G，满足(G)≤Δ.近年来,图的染色问题已由经典染色问题发展为种类繁多的新型染色问题(如点可区别边染色、Smarandachely邻点全染色和邻点可区别全染色等[4-6]).

2004年,张忠辅等[7]提出了邻点可区别全染色的概念,即在图G满足全染色的前提下,任意两个邻点的色集合不相同.并把所染颜色的最小数称为邻点可区别全色数，记作at(G)，且满足猜想at(G)≤Δ+3.2005年,李敬文等[8]对特殊图的Mycielski图的边染色进行深入研究. 2008年,李沐春等[9]对轮和路的广义-Mycielski图的星全染色做了针对性的研究,并得到它们的星全色数.学者们对于广义-Mycielski图的研究已经成为一个焦点. 2016年,张伟东[10]专门针对广义-Mycielski图的染色问题进行讨论. 2018年,张婷等[11]利用函数构造法,研究并确定了广义-Mycielski图的邻点可区别I-均匀全色数.

设G(V,E)是由顶点集V(G)和边集E(G)组成的简单连通图.其中，Δ和δ表示G中顶点的最大度和最小度,d(u)表示点u的度数,[1,n]表示从1到n这n个数组成的集合. Mycielski′s图是众多图类中重要的一类,以下给出Mycielski′s图的定义.

定义1[12]设G为简单连通图,如果满足:

(1)V(M(G))=V(G)∪V′∪{v}；

(2)E(M(G))=E(G)∪{uw′|u∈V(G),w′∈V′,uw∈E(G)}∪{w′v|w′∈V′}，其中，V′={w′|w∈V}且{v}∩{V(G)∪V′}=∅;

则称M(G)为G的Mycielski′s图.

在Mycielski′s图的基础上,文献[12]从圈的Mycielski′s图出发进行探究,首次引入了第一类广义-Mycielski′s图,具体定义如下:

定义2 设G(V,E)是拥有n个顶点的简单连通图,m为自然数,如果满足:

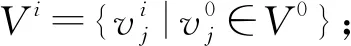
则称Nm(G)为G的第一类广义-Mycielski′s图 (图1，Nm(Pn)所示).

图1 第一、第二类广义-Mycielski′s图Fig.1 The first general-Mycielski′s graph Nm(Pn) and second general-Mycielski′s graph Mm(Pn)

随后,张东翰[13]针对路的广义-Mycielski′s图分两种情况进行讨论,并定义了第二类广义-Mycielski′s图.

定义3[13]设G(V,E)是拥有n个顶点的简单连通图,m为自然数,如果满足:

则称Mm(G)为G的第二类广义-Mycielski′s图(图1,Mm(Pn)所示).

对染色函数而言,一个自然的想法是能否将其从单元素的染色推广到集合下的着色,然后确定图的最小色数,目前不得而知.本文结合图的点染色和邻点可区别全染色，首先引入图的集合点染色概念,具体如下:

定义4 对于简单连通图G,令f是V(G)到集合X中非空子集的一个映射,其中，X={1,2,…,k},k为正整数,如果满足：

(1)∀u∈V(G),有|f(u)|≥d(u);

(2)对∀uv∈E(G),有f(u)≠f(v)且f(u)∩f(v)≠∅.

则称f为图G的集合点染色,简记作图G的k-SVC,并称s(G)=min{k|G具有k-SVC}为G的集合点色数.

在图染色研究中,构造染色函数法是确定色数最重要的工具之一.第一、第二广义-Mycielski′s图作为重要的两类图,广泛受到学者们的关注.本文应用构造染色函数法给出了第一、第二广义-Mycielski′s图的集合点染色及其对应的点色数.

1 主要结论

定理1设G是拥有n(n≥2)个顶点且最大度为Δ(Δ≥2)的简单连通图,同时s(G)=k, 则s(M(G))=max{k+Δ,n}.

情形1当γ>|V(G)|时,分两种情况进行讨论.

情形1.1若顶点集Vi中的最大度点相邻.

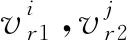
由Mycielski-图定义知,在G中的最大度顶点同时也是M(G)的最大度顶点. 故有：

2(k-1)=2k-2，

即集合点色数为2k-1.因此,M(G)有一个(k+Δ)-SVC染色.

下面构造M(G)的染色函数f*如下：

当1≤j≤n时，

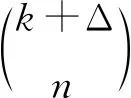
情形1.2若顶点集Vi中的最大度点不相邻.

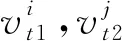
由Mycielski-图定义知,在G中是最大度顶点同时在M(G)也是最大度顶点. 从而有

即集合点色数为2k.因此，M(G)有一个(k+Δ)-SVC染色.

构造M(G)的染色函数f*如下：

当1≤j≤n时，

情形2当γ=|V(G)|时,分两种情况进行讨论.

情形2.1若顶点集Vi中的最大度点相邻.

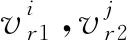
由Mycielski-图定义知,在G中的最大度顶点同时也是M(G)的最大度顶点. 同时有

即集合点色数为2k-1.因此,M(G)有一个(k+Δ)-SVC染色.

构造M(G)的染色函数f*如下：

当1≤j≤n时，

情形2.2若顶点集Vi中的最大度点不相邻.

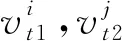
由Mycielski-图定义知,在G中是最大度顶点同时在M(G)也是最大度顶点. 从而有

即集合点色数为2k.因此,M(G)有一个(k+Δ)-SVC染色.

构造M(G)的染色函数f*如下：

当1≤j≤n时，

情形3当γ<|V(G)|时,分两种情况进行讨论.

情形3.1若顶点集Vi中的最大度点相邻.

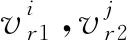
由Mycielski-图定义知,在G中的最大度顶点同时也是M(G)的最大度顶点. 同时有

又因为γ<|V(G)|=n,即集合点色数为n.因此,M(G)有一个n-SVC染色.

构造M(G)的染色函数f*如下：

当1≤j≤n时，

情形3.2若顶点集Vi中的最大度点不相邻.

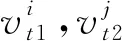
由Mycielski-图定义知,在G中是最大度顶点同时在M(G)也是最大度顶点. 从而有

又因为γ<|V(G)|=n,即集合点色数为n.因此,M(G)有一个n-SVC染色.

构造M(G)的染色函数f*如下：

当1≤j≤n时，

综上所述,结论成立.

定理2设G是拥有n(n≥2)个顶点且最大度为Δ(Δ≥2)的简单连通图,同时s(G)=k, 则G的第一类广义-Mycielski图的集合点色数为s(Nm(G))=k+Δ.

情形4若顶点集Vi中的最大度点相邻.

由第一类广义-Mycielski图定义知,在G中的最大度顶点同时也是Nm(G)的最大度顶点.同时有

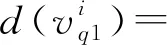
即集合点色数为2k-1,因此,Nm(G)有一个(k+Δ)-SVC染色.

构造Nm(G)的染色函数f*如下：

当1≤i≤m-1,1≤j≤n时，

情形5若顶点集Vi中的最大度点不相邻.

由第一类广义-Mycielski图定义知,在G中的最大度顶点同时也是Nm(G)的最大度顶点.从而有

即集合点色数为2k,因此Nm(G)有一个(k+Δ)-SVC染色.

构造Nm(G)的染色函数f*如下：

当1≤i≤m-1,1≤j≤n时，

综上所述,结论成立.

定理3设G是拥有n(n≥2)个顶点且最大度为Δ(Δ≥2)的简单连通图,同时s(G)=k, 则G的第二类广义-Mycielski图的集合点色数为s(Mm(G))=max{k+Δ,n}.

情形6当α>d(v)时,分两种情况进行讨论.

情形6.1若顶点集Vi中的最大度顶点相邻.

由第二类广义-Mycielski图定义知,在原图G中是最大度顶点，同时也是Mm(G)的最大度顶点.有

即集合点色数为2k-1.因此,Mm(G)有一个(k+Δ)-SVC染色.

构造Mm(G)的染色函数f*如下：

当1≤j≤n时，

情形6.2若顶点集Vi中的最大度顶点不相邻.

由第二类广义-Mycielski图定义知,在G中的最大度顶点同时也是Mm(G)的最大度顶点.从而有

2Δ=2k=k+Δ.

即集合点色数为2k,因此,Mm(G)有一个(k+Δ)-SVC染色.

构造Mm(G)的染色函数f*如下：

当1≤j≤n时，

情形7 当α=d(v)时,分两种情况进行讨论.

情形7.1若顶点集Vi中的最大度点相邻.

由第二类广义-Mycielski 图定义知,在G中的最大度顶点，同时也是Mm(G)的最大度顶点.有

即集合点色数为2k-1.因此,Mm(G)有一个(k+Δ)-SVC染色.

构造Mm(G)的染色函数f*如下：

当1≤j≤n时，

情形7.2若顶点集Vi中的最大度点不相邻.

由第二类广义-Mycielski图定义知,在G中是最大度顶点同时在Mm(G)也是最大度顶点.有

即集合点色数为2k.因此，Mm(G)有一个(k+Δ)-SVC染色.

构造Mm(G)的染色函数f*如下：

当1≤j≤n时,

情形8当α

情形8.1若顶点集Vi中的最大度点相邻.

由第二类广义-Mycielski图定义与α

构造Mm(G)的染色函数f*如下：

当1≤j≤n时,

情形8.2若顶点集Vi中的最大度点不相邻.

由第二类广义-Mycielski图定义与α

构造Mm(G)的染色函数f*如下：

当1≤j≤n时，

综上所述,结论成立.