基于改进离群算法的多元时间序列异常检测

苑津莎，甘斌斌，李 中，万 利，李 灿

(1.华北电力大学 电气与电子工程学院，河北 保定 071003; 2.国网四川省电力有限公司乐山供电公司，四川 乐山 614000;3.国网湖北省电力有限公司武汉供电公司，武汉 430000)

0 引 言

异常检测旨在检测出与主体数据存在显著差异的异常数据[1]，并挖掘出其中的信息价值。目前，异常检测已被广泛应用于金融、航天、医疗等诸多领域。这些领域中的数据集大多为具有时间性的多元时间序列数据，而多元时间序列具有海量、维数高、结构复杂且随时间不断变化等特点。因此，为了快速准确地检测出异常数据，防止数据源的异常工作状态造成恶劣影响，对多元时间序列进行异常检测尤为重要。

国内外学者针对不同类型的数据集，提出了一些多元时间序列异常检测的方法。LI J[2]提出了一种基于隐马尔可夫模型框架的多元时间序列异常检测方法；李海林[3]基于频繁模式发现的时间序列异常检测方法，克服了传统异常检测方法在增量式时间序列异常检测中准确率低的问题；戴仙波[4]提出了一种基于改进高斯核函数的边界网关协议异常检测方法，提高了模型分类的准确率；WANG X[5]提出了一种自学习在线异常检测算法，克服了时间序列的异常检测中异常无法定位的问题；余立苹[6]提出了一种基于高维数据流的异常检测算法，解决了传统算法精确度无法保证和计算时间过长的问题，实现了高维数据流的异常检测；BREUNIG M M等[7]提出了基于密度完成异常检测的方法，解决了子集密度不同所导致的混合错误问题；王欣[8]提出了两阶段的多元时间序列异常检测方法，先利用K-means对数据聚类，再通过循环嵌套算法和剪枝规则快速地完成异常检测。现有的多元时间序列异常检测方法虽提高了算法效率，但准确率却没有得到很好地提高。

为此，文章提出一种基于改进离群算法的多元时间序列异常检测方法。考虑多元时间序列的多个维度特征之间的相似性，基于最小距离度量改进传统的离群点检测方法，利用改进后离群算法对多元时间序列异常进行数值化表达，从而实现多元时间序列的异常检测。运用该算法进行实验验证，结果表明该算法检测性能良好。

1 基于最小距离的离群算法

1.1 主成分分析与最小距离度量

主成分分析(Principal Component Analysis,PCA)[9]作为一种常用的线性降维方法，其功能是将高维空间中的数据样本映射到低维空间中。对于一个多元时间序列X=[x1,x2, …,xn]，可以表示成一个n×m的矩阵，即X=(xij)n×m。xij表示第i个时间节点的第j个维度观测值，n和m分别表示多元时间序列的时间长度和观测维度。

主成分分析首先需要计算多元时间序列多个观测维度变量之间的协方差，得到协方差矩阵Sn×m，利用奇异值分解对协方差矩阵进行特征值和特征向量分解，得到按特征值大小排列的对角矩阵Vm×m=diag(λ1,λ2, ...,λm)和对应的特征矩阵Um×m=[u1,u2, ... ,um],如式(1)所示。

(1)

根据特征值的大小，选择前h个特征向量构成特征空间，进而得到相应的主成分。对应的时间序列的特征为主成分，其计算式如式(2)所示。

Yn×h=Xn×mUm×h

(2)

式中：Yn×h为降维后的时间序列特征值。

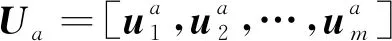
dij=1- |cosθij|

(3)

式中：cosθij为第个i基向量和第j个基向量的夹角。

对于两个多元时间序列，基于式(3)可计算前h个特征向量中任意两个向量之间的夹角距离矩阵Dh×h=(dij)h×h。

基于最小距离矩阵Dh×h，最小距离度量方法与传统Eros距离度量方法的思想一致，即找到一组匹配具有最小距离的最优解，并取得最小距离度量。该问题可归纳为一个线性规划问题，目标函数如式(4)所示。

(4)

式中：(cij)h×h是决策变量矩阵，且当cij=1时，表示夹角距离矩阵元素dij参与最小距离度量。

该线性规划问题为一个线性任务分配问题，选择匈牙利算法[10]对其进行求解，目的是求得一个使总距离代价最小的决策变量矩阵，从而得到最终的最小距离度量dMEros=MEros(An1×m,Bn2×m,h)。

1.2 基于最小距离优化的局部离群因子算法

多元时间序列经过PCA进行特征表示后，样本被映射为高维空间中的点群。由于数据源的稳定性，大部分的点都相对集中。基于该特点，局部离群因子(Local Outlier Factor，LOF)算法[11]通过定义LOF来描述每一个样本的离群程度。不同于阈值的硬性划分，对于给定含有n个样本的集合以及预期离群样本数k,LOF算法的任务是从集合中通过LOF挖掘出所有样本中离群程度最显著的k个样本，实现异常点的检测。基于最小距离优化的局部离群因子通过o点的k距离、o点的k距离邻域、可达距离、局部可达密度四个概念来定义。

1)o点的k距离

定义数据集中样本点o到任意点p的最小距离为dMEros(o,p)，样本o点到以o为中心的第k个最邻近样本的距离为o点的k距离，记为dk(o)，其计算式如式(5)所示。

(5)

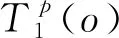
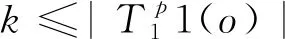
2)o点的k距离邻域

对于数据集中的任意点o，数据集中所有到点o的距离不大于dk(o)的点的组成的集合，称之为o点的k距离邻域，记为Nk(o)，其计算式如式(6)所示。

Nk(o)={p∈χ│p≠o,dMEros(o,p)≤dk(o) }

(6)

式中：x为多元时间序列数据集中所有数据样本的集合。

3)可达距离

如图1所示，对于样本点o，关于样本点p的可达距离定义如式(7)所示。

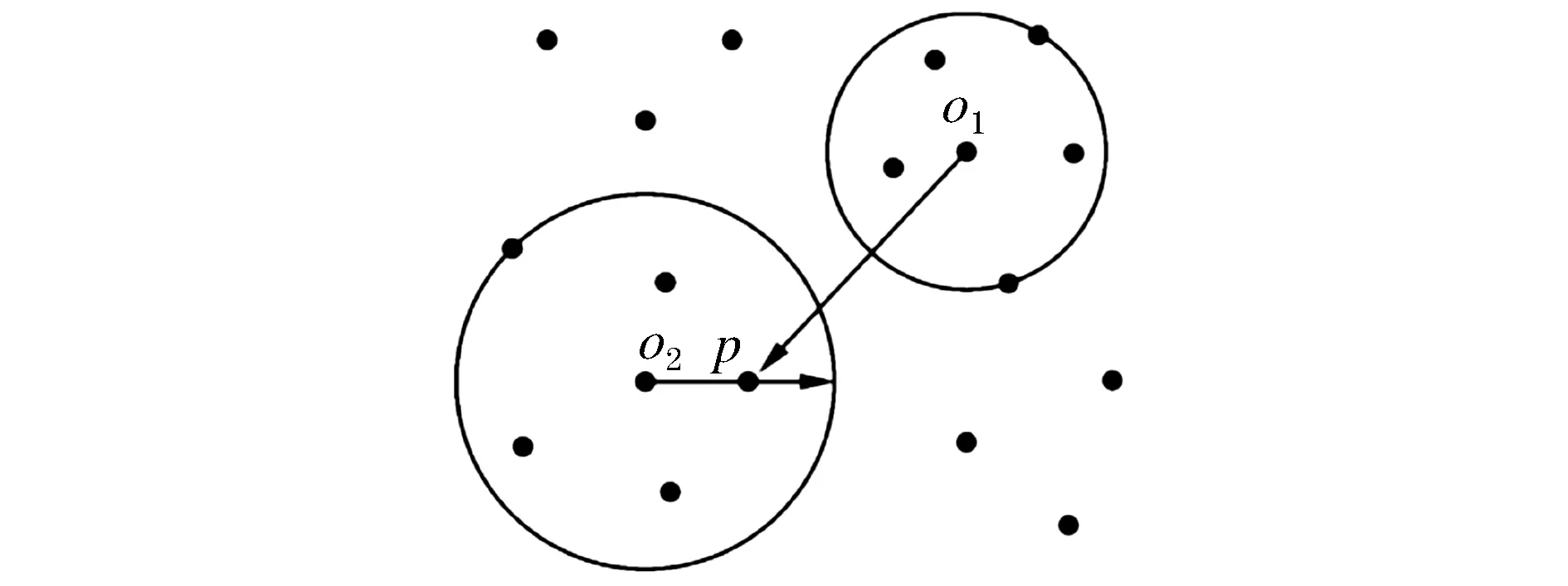
图1 可达距离示意图

Rd(o)=max{dk(p),dMEros(o,p)}

(7)

4)局部可达密度

样本点o的局部可达密度定义为样本点o到o点的k距离邻域内所有点的平均可达距离的倒数，如式(8)所示。

(8)

通过以上四个定义，可以定义出度量样本点o离群程度的局部离群因子，如式(9)所示。

(9)

以样本点o的局部可达密度为基准，对o点的k距离领域内所有样本点的局部可达密度进行求和，通过取平均值来度量样本点o的密度与周围样本点的密度差异，从而对样本点o的离群程度进行量化。基于最小距离优化离群算法的多元时间序列异常检测流程如图2所示。

2 实验及结果分析

为验证算法的实际效果，选用多元时间序列标准数据集，将基于欧氏距离度量的离群算法与所提改进后的离群算法进行比较，通过对比两种方法的检测率(Detecton Rate，DR)、误报率(False Positive Rate，FPR)、漏报率(False Negative Rate，FNR)以及算法的计算时间来验证改进后离群算法的性能。实验数据选用3组多元时间序列数据集：MRN_measles[12]、Face(all)[13]和Trace[13]。表1为3组数据集信息的描述。

表1 实验数据统计

2.1 离群算法邻域k值的确定

在基于离群算法进行异常检测的实验中，邻域k值的大小对算法的性能有着至关重要的影响，如果邻域k值太小，则可能无法检测出异常簇；如果邻域k值太大，则可能将正常点检测为异常值。表2列举了3组数据集在邻域k值不同时，离群算法异常检测的准确度。异常检测的准确度EAcc定义如下：

式中：m为原始数据集中的真实异常点数；n为算法检测到的真实异常点数。

由表2可知，当k=25时，MRN_measles数据集异常检测的准确度最高；当k=15时，Face(all)数据集异常检测的准确度最高；当k=20时，Trace数据集异常检测的准确度最高。图3为邻域k值与计算时间的关系图，由图可知，在3组数据集上算法的计算时间均随着邻域k值的增大而增加。

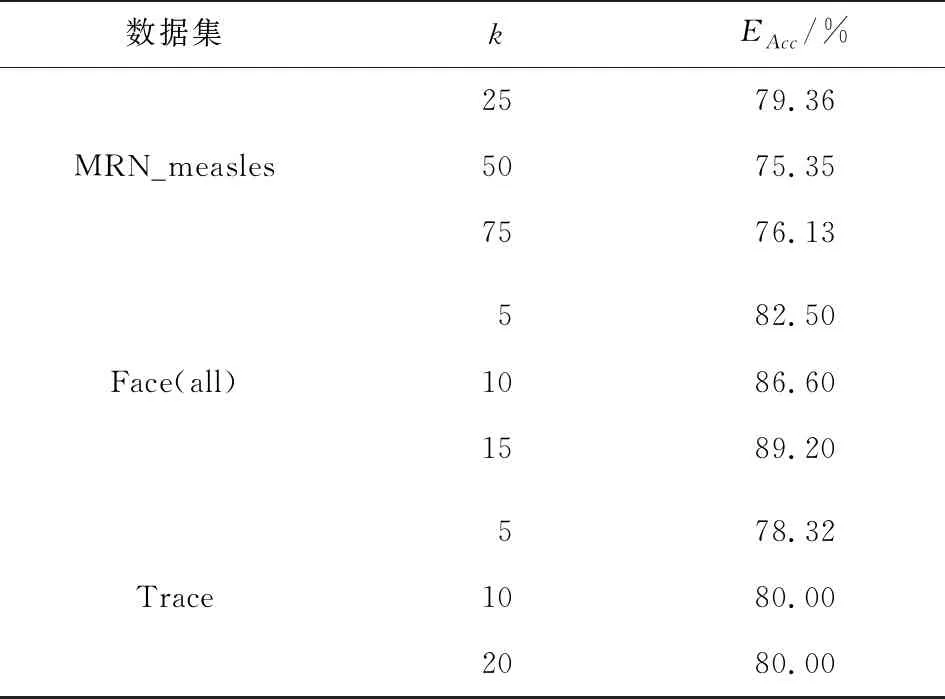
表2 邻域k值对算法精确度的影响

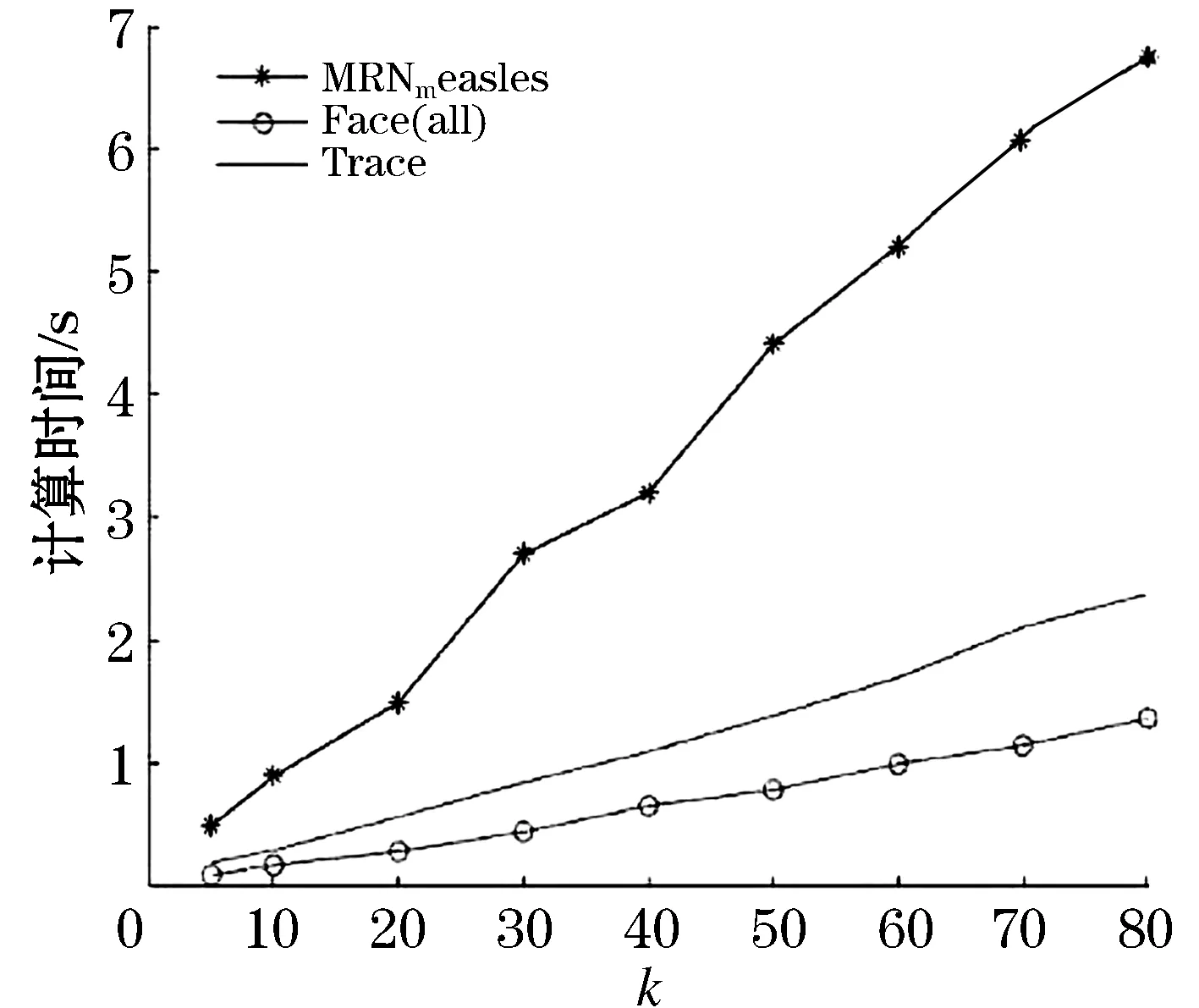
图3 计算时间与k值的关系

2.2 算法准确性与可用性

为了更准确地验证运用改进离群算法进行多元时间序列异常检测的有效性，在对比实验中，分别选取3组多元时间序列数据集准确度较高且计算时间较短时所对应的邻域k值进行实验。实验通过检测率、误报率、漏报率来衡量算法的性能。计算式如下：

式中：X代表数据集合；Y代表X中的异常数据集合；Y′代表离群算法检测出的异常数据集合。

运用传统离群算法和改进后离群算法分别对3种数据集进行多元时间序列异常检测，结果如图4～6所示。

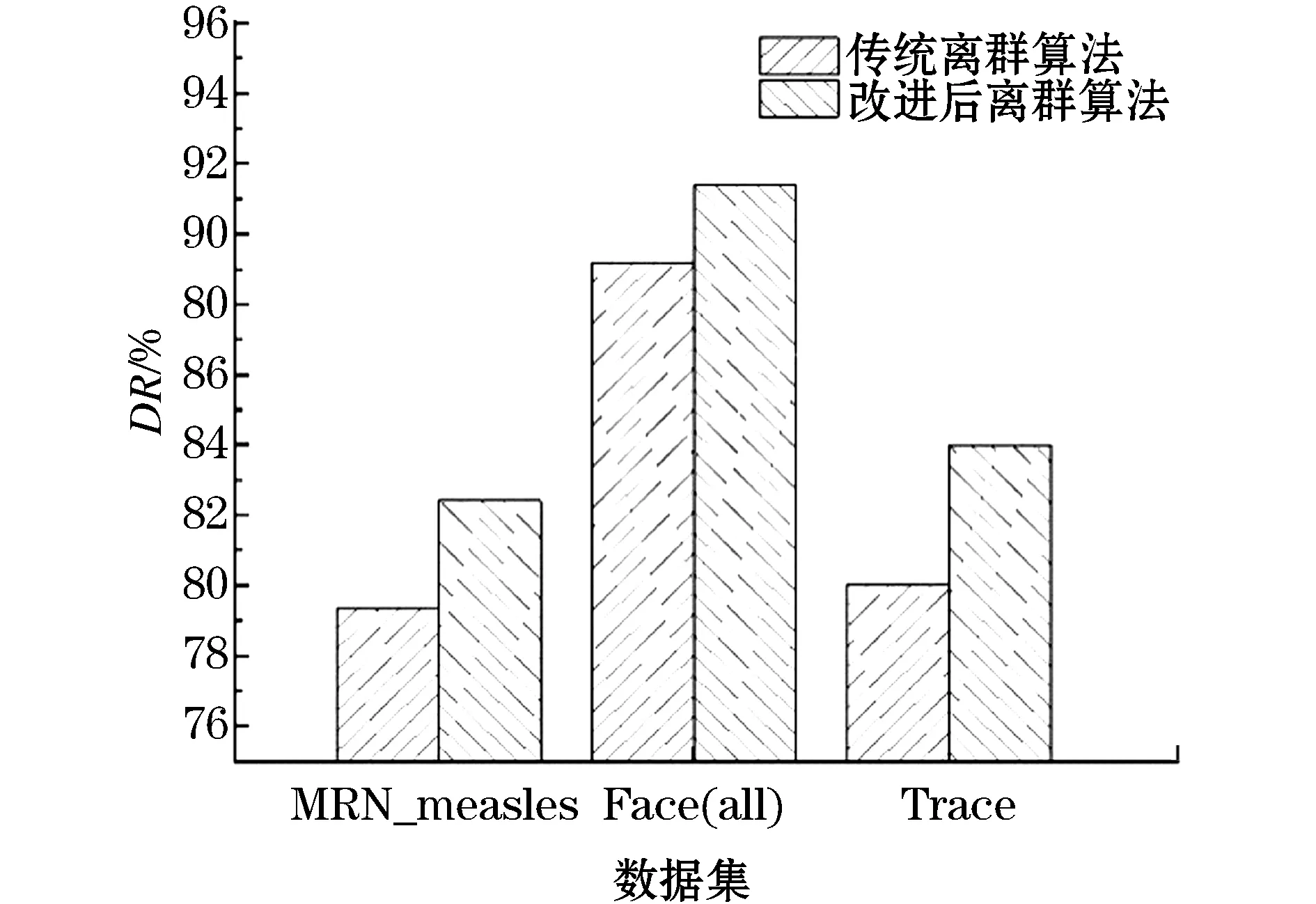
图4 两种不同算法下的检测率对比

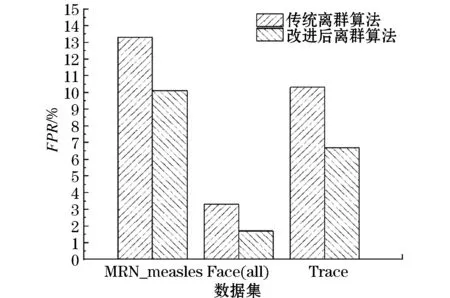
图5 两种不同算法下的误报率对比

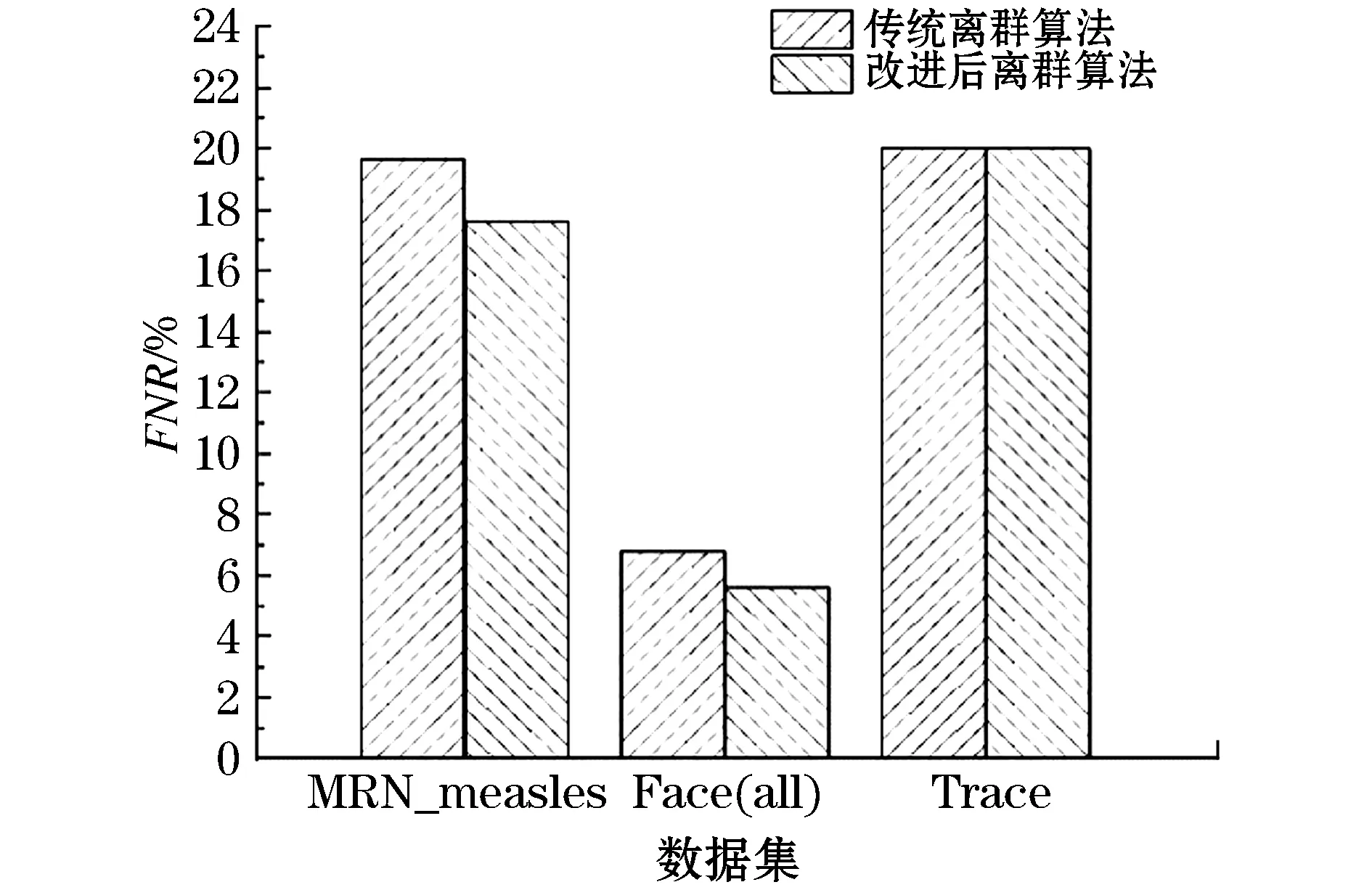
图6 两种不同算法下的漏报率对比

实验结果显示，在检测率方面，所提算法与传统离群算法相比，在MRN_measles、Trace和Face(all)数据集中检测率分别提高了3.2%、5.1%和3.0%；在误报率方面，所提算法与传统离群算法相比，在MRN_measles、Trace和Face(all)数据集中检测率分别降低了3.4%、3.0%和1.2%；在漏报率方面，所提算法与传统离群算法相比，虽然在数据集Trace的实验中漏报率没有降低，但是在数据集MRN_measles和Face(all)的实验中漏报率分别降低了2.1%和1.4%。通过这3组数据集和3项指标的评估实验表明，相较于传统的离群算法，文中提出的改进后的离群算法具有更好的准确性和可用性。

2.3 算法的计算时间

本组实验采用随机数发生器产生1 000～10 000大小不等、服从正态分布且具有不同密度的聚类数据集，通过比较传统离群算法与改进后离群算法的计算时间来进行对比实验[14-20]。

由图7可知，两种算法的计算时间随着实验个数的增加而增加。在实验个数较少的情况下，传统离群算法的计算时间低于改进后离群算法；当实验个数趋近7 000时，改进后的离群算法与传统离群算法的计算时间逐步接近；直至实验个数达到9 000～10 000时，两种算法的计算时间几乎相等。与传统离群算法相比，改进的离群算法在提升多元时间序列异常检测性能的同时，计算时间随着数据量的增加产生较小增幅，达到了较好的检测效果。

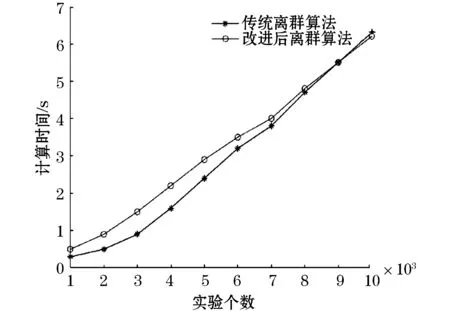
图7 两种不同算法的计算时间对比

3 结 语

提出一种基于最小距离改进的多元时间序列异常检测算法，弥补了传统离群算法中时间轴弯曲所导致的误检、误报等不足。通过MRN_measles、Face(all)和Trace 3组多元时间序列标准数据集进行实验，将基于欧氏距离度量的离群算法与改进后的离群算法进行比较，结果表明，运用改进后的离群算法进行检测，3种数据集的检测率得到明显提高，且误报率和漏报率得到有效降低。采用随机数发生器产生的数据集进行实验，将两种算法的时间代价进行对比，结果表明，两种算法的时间代价会随着数据量的增加逐步趋近，且改进后的离群算法在时间代价上具有较小的增幅。因此，改进后的离群算法对多元时间序列的异常检测具有较良好的性能。