液压缓冲器阻尼与冲击特性仿真分析
2020-08-03方永寿陈轶杰张亚峰代健健
方永寿, 陈轶杰, 张亚峰, 代健健
(1.中国航天科工集团第206研究所,北京 100854;2.金华职业技术学院机电工程学院,金华 321000; 3.中国北方车辆研究所底盘部件技术部,北京 100072)
军用车辆通常需要具备在越野路面高速行驶的能力,悬挂系统会频繁承受来自地面的振动冲击,为满足减振缓冲的需要,在压缩行程的末端会布置大行程液压缓冲器,通过阀系节流可瞬间产生足够的熄振效能,以防止出现悬挂击穿的现象,确保车辆的综合行驶性能,比如德国的豹2主战坦克、美洲狮步兵战车等均采用了大行程液压缓冲器;由于中国在该领域理论建模方面的研究相对滞后,与国外相比存在较大差距[1-3],所以军事特种车辆仍旧采用的是橡胶缓冲器,存在压缩行程有限、缓冲能力不足等问题,制约了悬挂系统技术的进一步发展。针对这种情况,急需深入开展军用车辆液压缓冲器的数学建模和示功特性的仿真分析研究,为产品的研制开发和悬挂系统特性优化奠定基础。在前人研究的基础上,充分考虑了活塞与油缸的偏心误差及油液的可压缩性,并研究了其对液压缓冲器综合特性及缓冲力的影响;建立了缓冲器动态冲击数学模型,仿真分析瞬态冲击工况下缓冲器的冲击特性,并对比分析关重参数的影响。
1 液压缓冲器结构
图1为液压缓冲器结构简图,中空的活塞杆套装在缸筒内,上端活塞与缸筒之间形成环形缝隙,在运动过程中产生节流效果形成阻尼力,活塞杆通过螺纹连接有组合式活塞,活塞周向布置有单向球阀,与环形缝隙配合使用达到衰减外界冲击振动的目的。在缸筒外部安装有橡胶套,与缸筒之间形成的环形腔为储油室,在活塞往复运动过程中通过橡胶的挤压变形达到为缸筒内腔补偿油液的作用。在设计液压缓冲器时通常按理想状况考虑,但实际制造、装配过程中会产生一定的偏差,且油液不是绝对不可压缩的,这些误差影响了液压缓冲器的特性表现,其影响规律需要作进一步的研究。
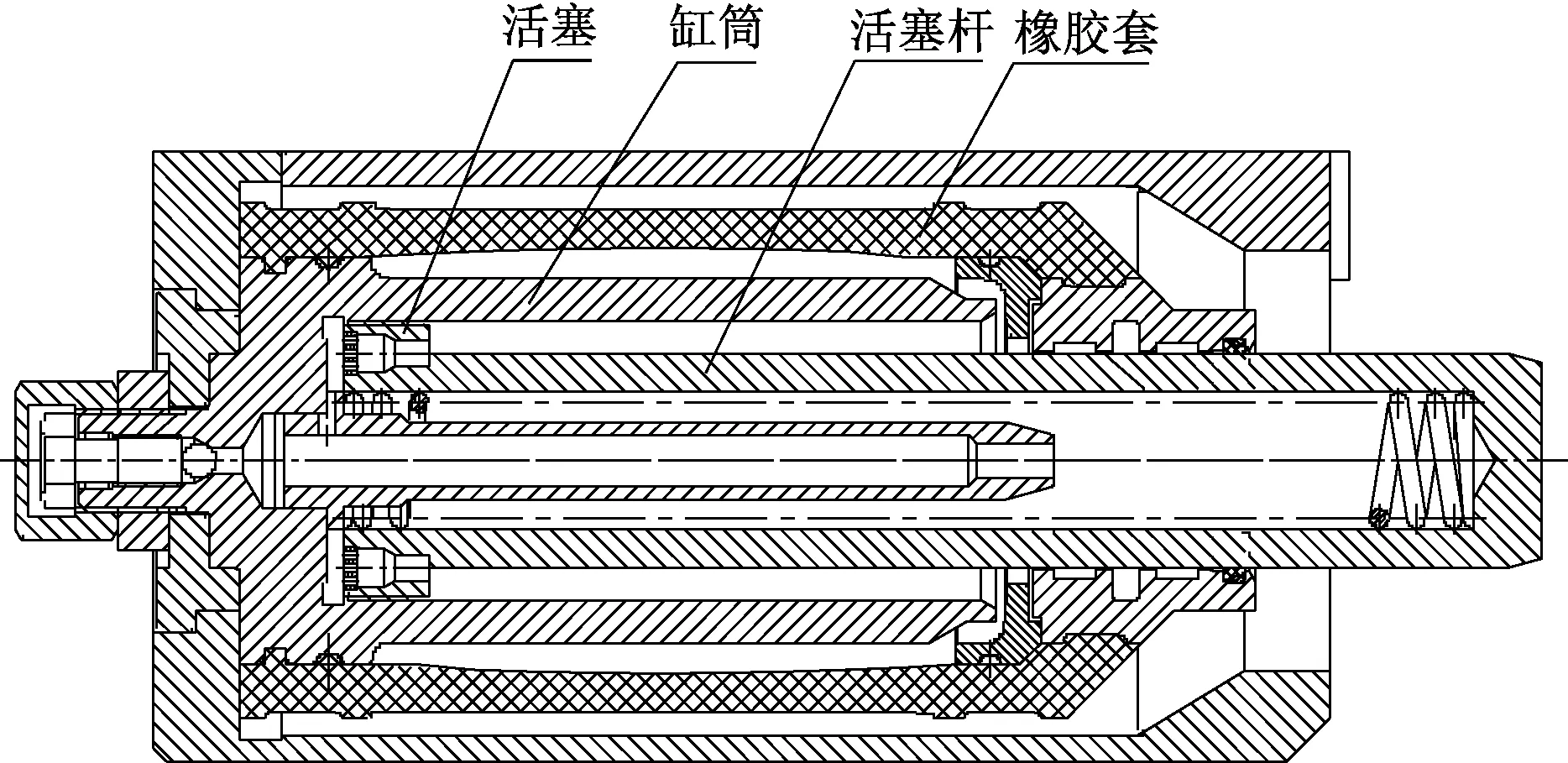
图1 液压缓冲器结构图Fig.1 Hydraulic buffer structure diagram
针对图1中的液压缓冲器,深入开展阻尼与冲击特性理论建模和仿真分析研究,并明晰关键要素对特性参数的影响规律。
2 液压缓冲器示功特性解析计算
2.1 偏心环形缝隙流的特性
当缓冲器在受到冲击后活塞与缸筒之间容易出现不同轴的现象,工作时则会出现偏心环形缝隙对油液节流的情况,图2所示即为偏心环形缝隙的结构简图。h0为偏心缝隙宽度,是圆周角θ的函数;e为缝隙的内外径偏心距;rp和R分别为偏心缝隙的内外半径。
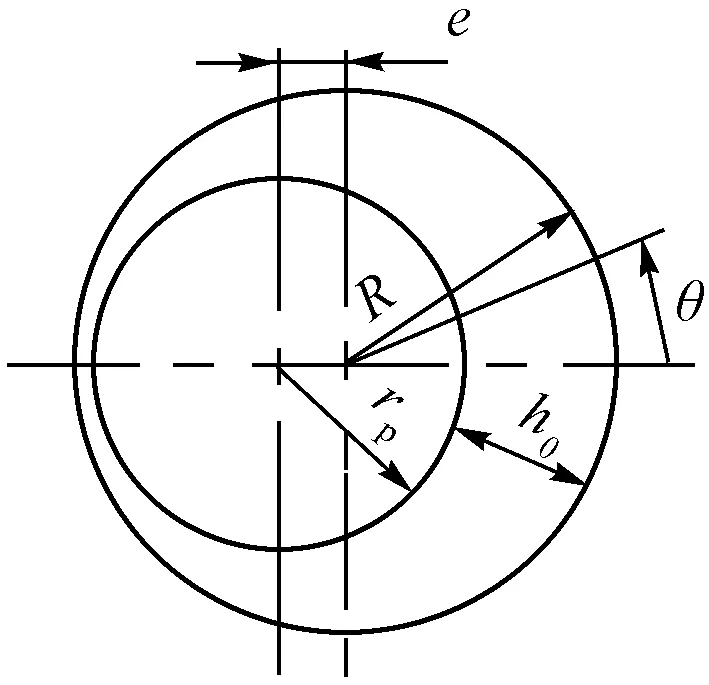
图2 偏心环形缝隙示意图Fig.2 Eccentric annular gap diagram
设δ=R-rp为同心时的缝隙宽度,并令[4]:
(1)
式(1)中:ε为偏心率。
由流体力学相关理论容易推出[5-6]:
h0=δ(1+εcosθ)
(2)
将偏心环形缝隙分解为多个微元段,由微元dθ所夹的两个微元弧段可以近似等效为Bk=rpdθ。
根据边界层理论时均速度分布可知如下无量纲关系式[7-8]:
(3)
式(3)中:ρ为油液密度;τw为壁面切应力;ν为油液运动黏度;y+为无量纲至壁面距离。
由式(3)可知:
(4)
推导偏心缝隙壁面在流体作用下的受力情况如下:
(5)
式(5)中:l为缝隙长度;dFm为壁面微元摩擦力;dFy为偏心缝隙微元面积压力差。
进一步整理得:
(6)
联立式(4)、式(6),有:
(7)
可以看出,在区间θ∈(0,π)中,随着角度的增加,流层厚度也在逐渐增大,而缝隙宽度h0却在不断减小,并在θ=π时达到最小。由此引出一个新的问题,即需要考虑缝隙中黏性底层、过渡层与缝隙半宽度之间的关系。当黏性底层和过渡层厚度之和大于等于缝隙半宽度时,对数律层将消失,从此处开始缝隙中的流体速度分布变为两层结构;当黏性底层的厚度大于等于缝隙半宽度时,过渡层与对数律层都将消失,从此处开始缝隙中的流体只有一层结构。
设对数律层和过渡层都消失时的临界圆周角为θ1,通过上述分析可知黏性底层最大厚度为
(8)
令:
(9)
推导得出:
(10)
设对数律层消失时临界圆周角为θ2,已知过渡层最大厚度:
(11)
令:
(12)
推导得出:
(13)
对圆周角进行积分处理,即可推导偏心环形缝隙的流量解析式:
(14)
将式(3)~式(8)、式(10)及式(13)代入式(14)同时合并同类项得:
(15)
2.2 缓冲器外特性仿真分析
运用所推导出来的偏心环形缝隙流量解析式,对液压缓冲器特性的关键影响参数进行编程计算和分析讨论。由图3可看出,随着油液动力黏度μ的增大,压差Δp逐渐越大。μ=0.069 7 Pa·s时的压差相对于μ=0.019 Pa·s时的压差增加了150%以上,说明动力黏度对缓冲器的特性影响很大,而油液的温度、含气量、压力等对油液的动力黏度都有一定的影响,在缓冲器设计时,都是要考虑的因素,合理选择动力黏度,可以使缓冲器更好地发挥作用;由图4可以看出,压差Δp随缝隙宽度h0的增加呈近似抛物线下降,开始时下降迅速,随着h0的增大,下降趋势减缓,可见压差Δp对缝隙宽度h0的变化比较敏感,设计时,h0不宜过大,否则将降低对高速冲击的缓冲 效率,达不到理想的缓冲效果,所以合理地选择活塞与缸筒之间的环形缝隙宽度,有效抑制h0,是设计出性能满足要求的缓冲器的重要环节。

图4 环形缝隙宽度对压差的影响Fig.4 The influence of the annular gap width on the pressure difference
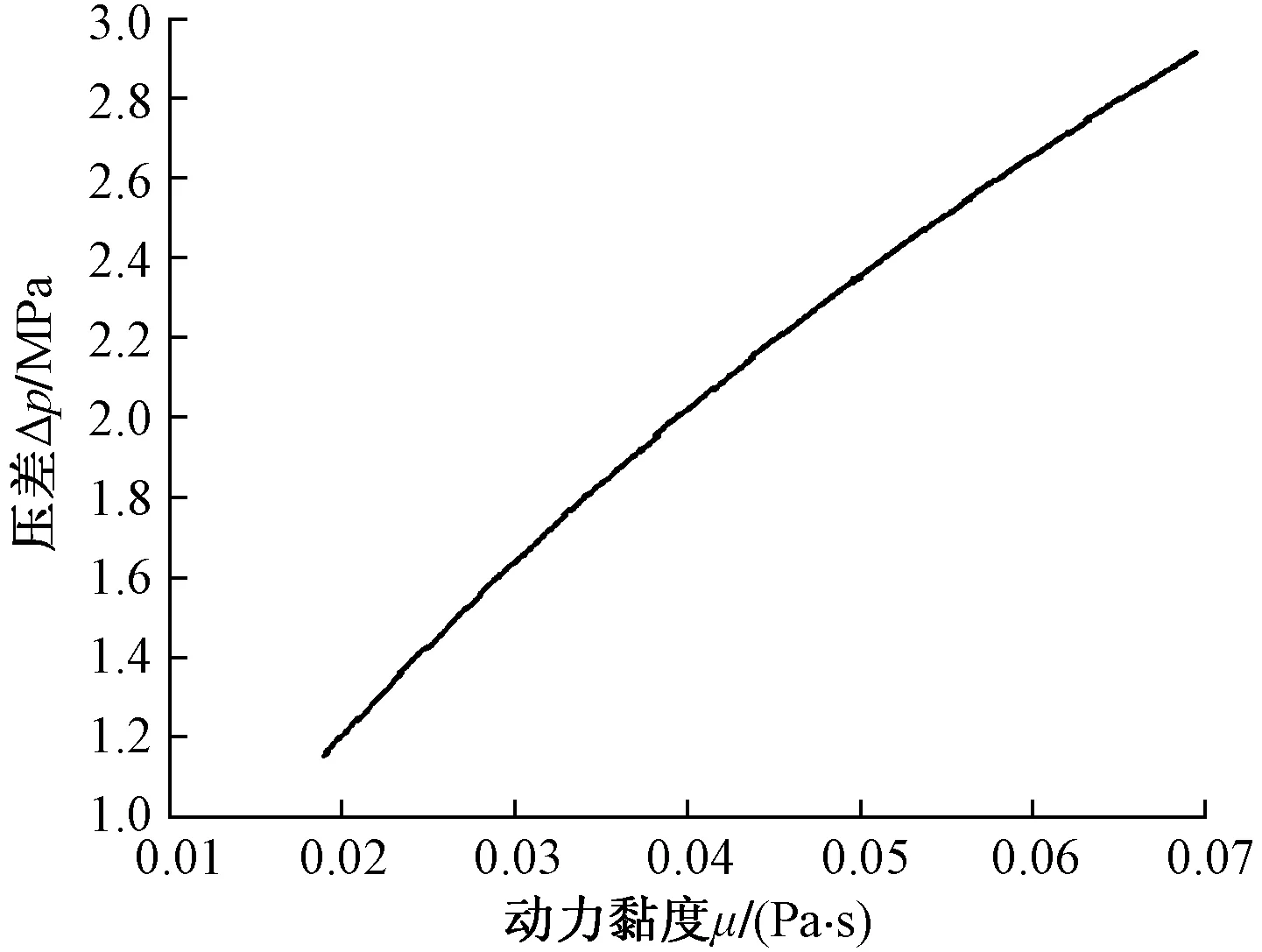
图3 偏心环形缝隙动力黏度对压差的影响Fig.3 The influence of the dynamic viscosity of the eccentric annular gap on the pressure difference
图5为缝隙压差随活塞速度的变化曲线,随着缓冲器运动速度的增大,缝隙两端压差也呈现出明显的上升趋势。图6为环形缝隙偏心率ε与压差的关系,可以看出随着ε的增大,Δp呈减小趋势,且降速逐步加快,但缓冲器在实际使用过程中,由于经常受到侧向力作用,设计时通常取ε=1。

图5 偏心环形缝隙过流速度对压差的影响Fig.5 The influence of over-current velocity of eccentric annular gap on the pressure difference

图6 环形缝隙偏心率对压差的影响Fig.6 The influence of annular gap eccentricity on the pressure difference
3 液压缓冲器动态冲击与复位过程数学建模
3.1 缓冲器冲击数学建模
在缓冲器缝隙节流解析计算的基础上,进一步建立动态缓冲过程的数学模型,缓冲器的缓冲过程如图7所示,冲击载荷作用于活塞杆底部,通常与悬挂系统摆臂相接触,缓冲器内部油液所产生的压力作用于活塞表面,用于抵消外部冲击力,可建立油液的流量连续性方程[9-11]为

图7 缓冲过程原理图Fig.7 Buffer process schematic diagram
(16)
式(16)中:Cq为流量系数;ρ为油液密度;x为缓冲器行程;v为活塞运动速度。
由式(16)并结合缓冲器内外受力情况推导缓冲器在冲击过程中的速度、压差与位移微分方程组如下:
(17)
3.2 缓冲器复位过程数学建模
液压缓冲器在复位过程中单向阀打开,油液经过单向阀、节流孔和缝隙由内腔流向外腔。按照前面对缓冲行程的分析方法,建立复位过程的数学模型,得到微分方程组如下:
(18)
进一步得到液压缓冲器的缓冲力为
F=Δp(A1-A2)
(19)
3.3 缓冲器冲击过程仿真分析
对缓冲器全行程进行仿真计算得到如图8所示的行程随时间的变化曲线。可知,缓冲行程用了约0.31 s,回复行程只用了0.04 s,回程迅速。
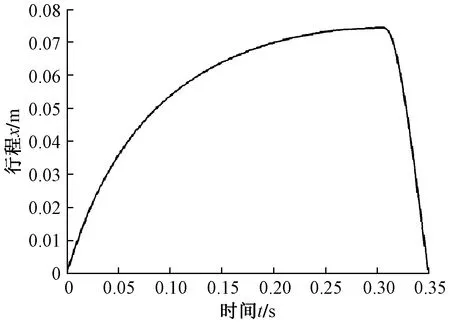
图8 缓冲器行程-时间关系Fig.8 Buffer stroke-time relation
图9为仿真得到的速度与时间的关系曲线。可知,缓冲行程速度下降缓慢,回复行程速度急速下降。
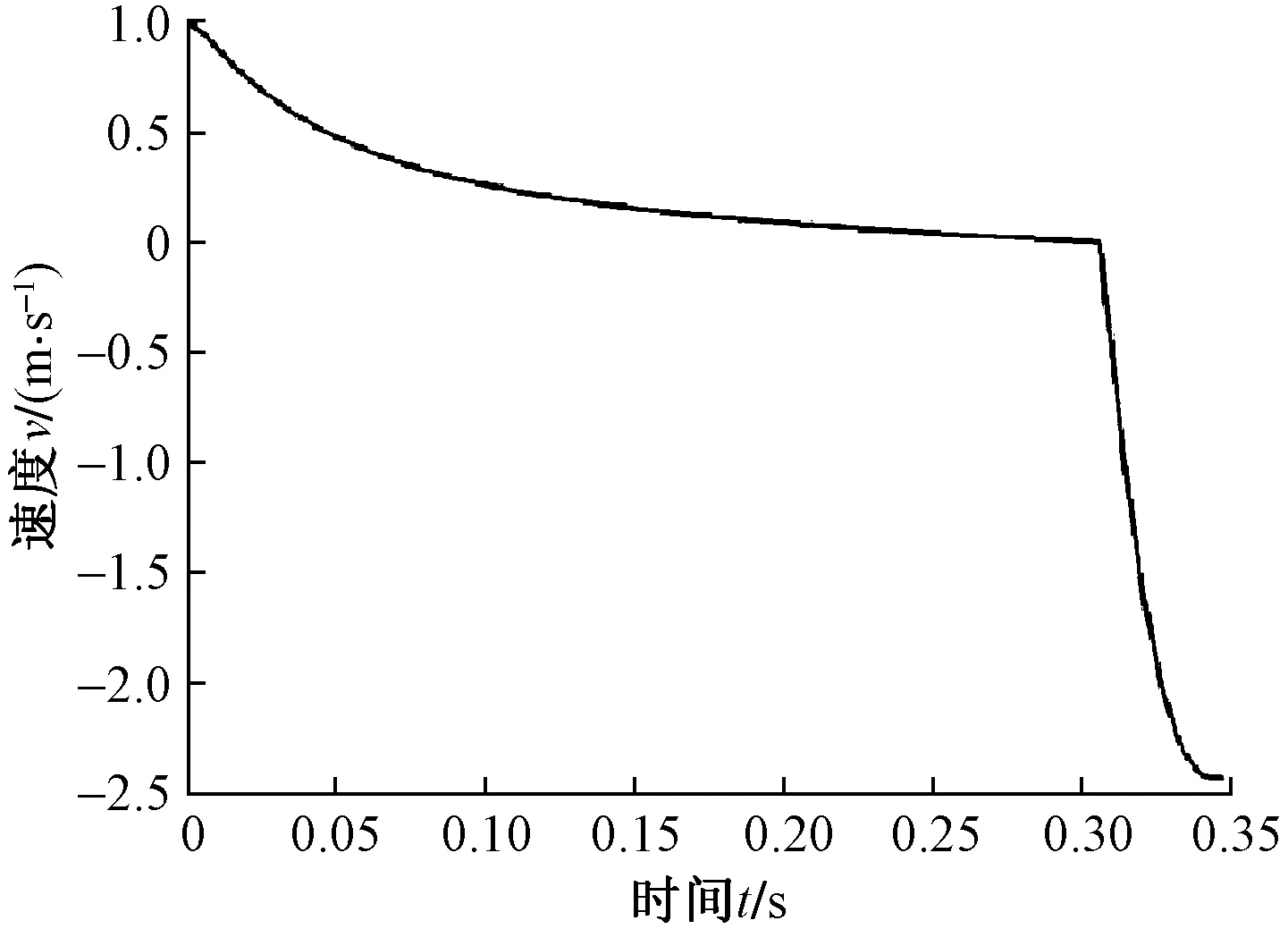
图9 缓冲器速度-时间关系Fig.9 Buffer velocity-time relation
图10为仿真得到的压差与时间的关系曲线。可知,液压缓冲器在前时间0.31 s内是缓冲过程,在0.31 s时缓冲行程(工作行程)结束。0.31 s之后缓冲器活塞在背压弹簧作用下开始释放缓冲能量,并转变为复原工作行程,缸筒外部的橡胶套通过弹性变形挤压储油腔内的油液,使其迅速回流到工作腔室,复位行程从0.31 s开始到0.35 s结束,回程时间明显小于缓冲行程,以便满足频繁冲击的使用需求。
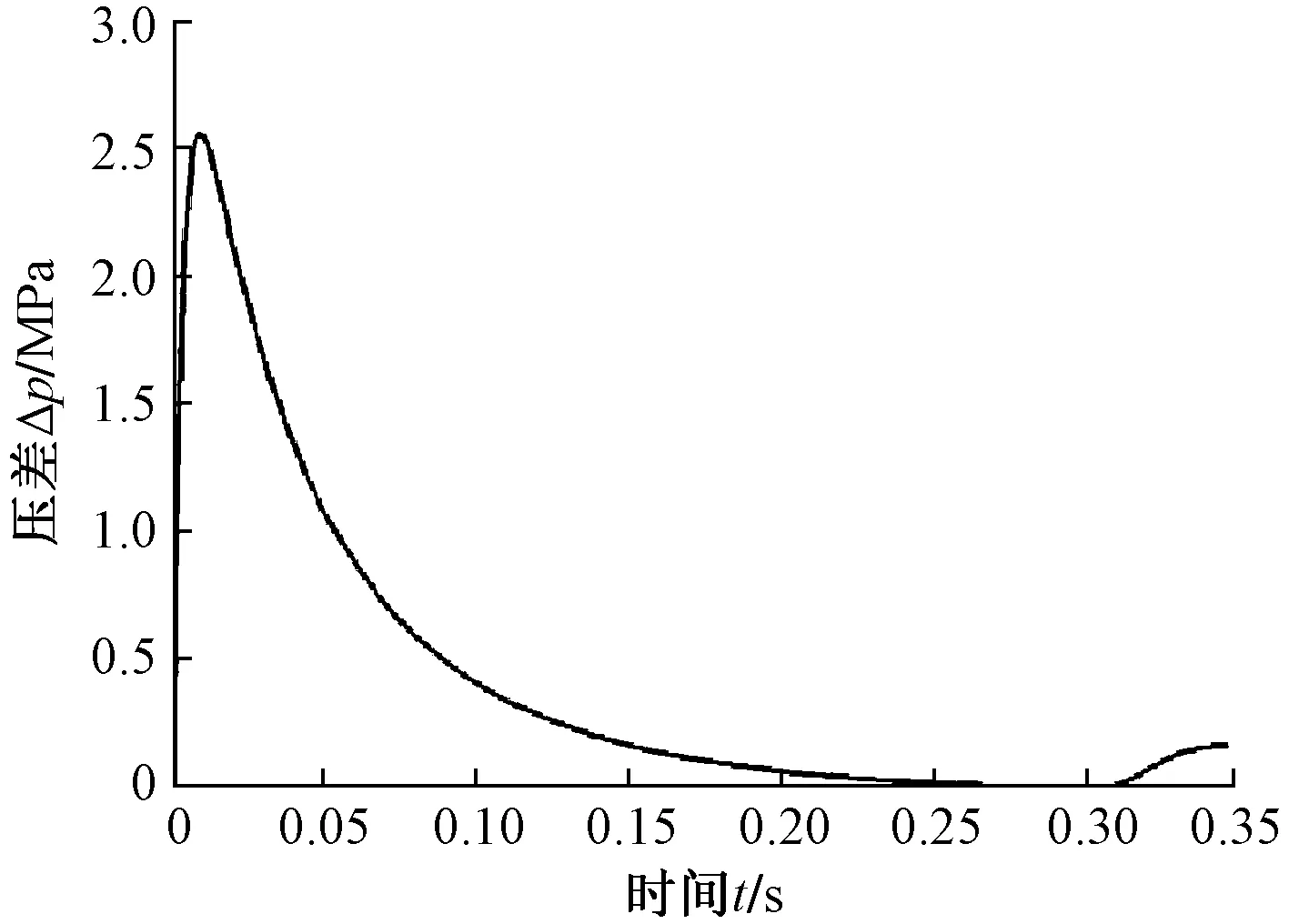
图10 缓冲器压差-时间关系Fig.10 Buffer pressure difference-time relation
图11所示为缓冲器示功图试验对仿真对比曲线,即液压缓冲器在整个缓冲和复位过程中的缓冲力随行程的变化关系曲线,曲线包络的面积为缓冲器全过程所吸收的能量,示功图很好地反映了缓冲器在工作行程和回复行程对能量的吸收和耗散特性,其中缓冲力峰值试验与仿真对比误差为5%,验证了数学建模的正确性,对缓冲器设计具有重要的意义。
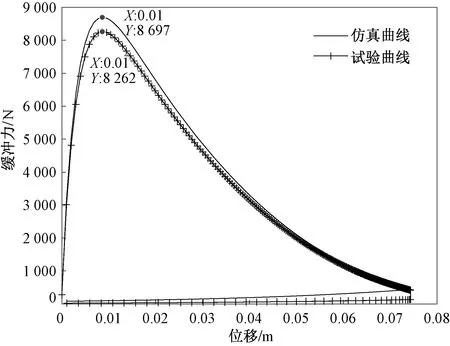
图11 液压缓冲器示功图Fig.11 Hydraulic buffer indicator card
进一步,运用四阶龙格库塔数值计算方法求解缓冲器缓冲过程的微分方程组,设定初始值Δp=0 MPa,x=0,v=1 m/s,进行数值计算并开展缓冲器的冲击特性影响因素分析,如图12、图13所示。可以看出,随着冲击初速度的增加,缓冲力峰值和活塞运动位移出现明显增大的现象,示功特性的包络面积也随之增加,用于吸收更多的外界振动能量;当冲击载荷一定时,随着节流缝隙的减小,缓冲力峰值呈现出明显的增大趋势,且能够有效抑制活塞位移的变化,所以可根据熄振性能的需要适当调整节流缝隙参数,以满足使用需求。
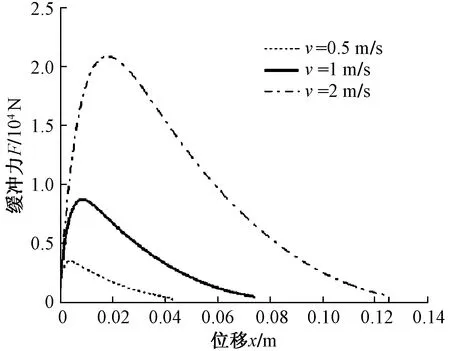
图12 初始冲击速度对缓冲力随缓冲行程变化的影响Fig.12 The influence of initial impact velocity on buffer force with buffer stroke change
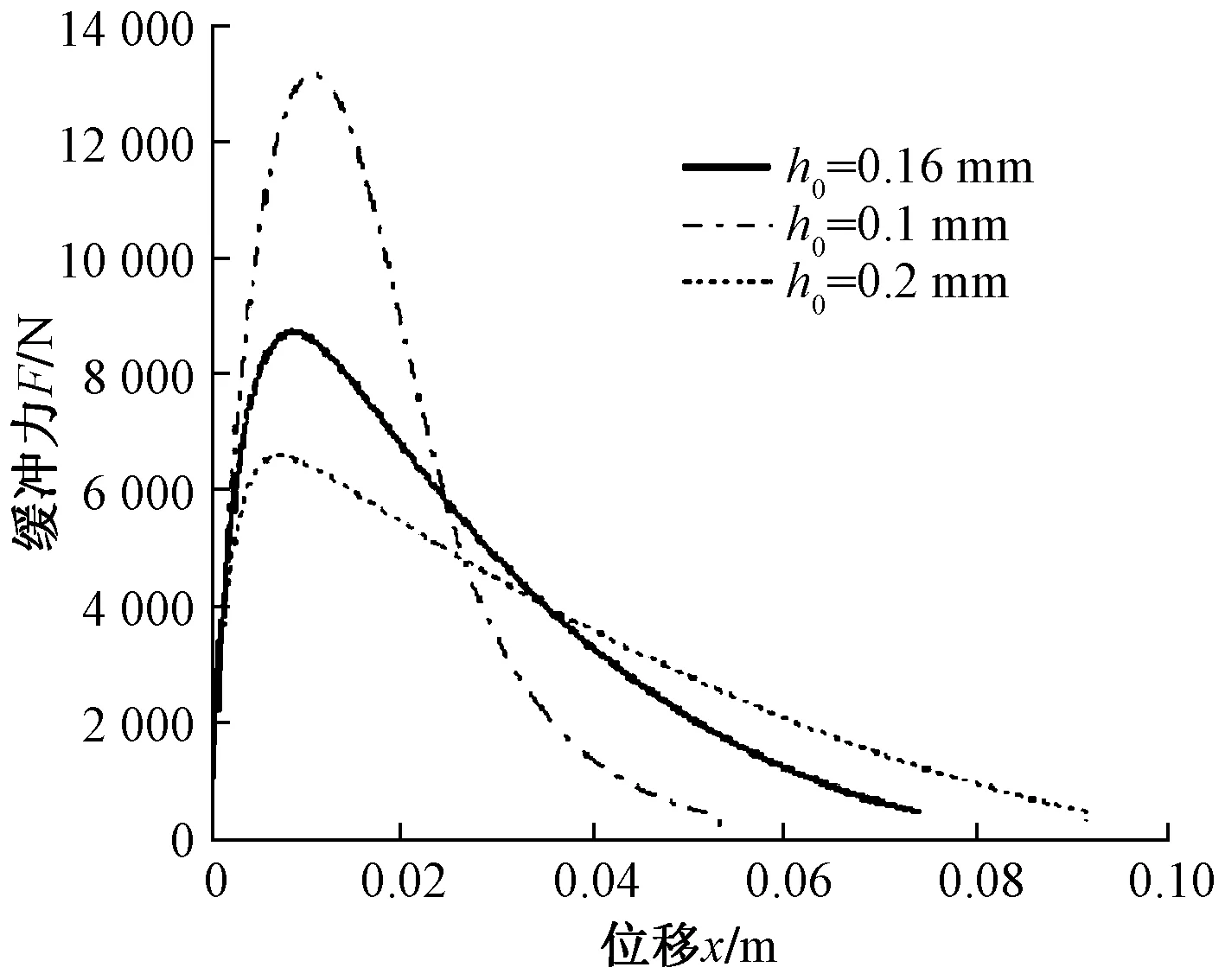
图13 缝隙宽度对缓冲力随缓冲行程变化的影响Fig.13 The influence of gap width on buffer force with buffer stroke change
4 结论
运用边界层理论推导了偏心环形缝隙的流量解析式,并用于液压缓冲器的理论建模,得到以下结论。
(1)活塞缝隙的结构参数和油液动力黏度对缓冲器的缓冲和能量耗散起重要作用,所以设计时应综合考虑节流特性,避免出现缓冲吸收能量效率低或瞬态冲击峰值过大的缺陷。
(2)构建了完整的液压缓冲器压缩与复原全行程动态冲击数学模型,可准确模拟其真实的工作过程,能够为液压缓冲器的研制与设计提供重要的理论支撑。
(3)从仿真对比分析可以看出,随着冲击速度的增大,缓冲器将有效地吸收更多的振动能量,示功图面积明显增大,证明结构设计合理。
(4)节流缝隙参数的变化对缓冲器的熄振能力具有决定性影响,缝隙宽度越小,所产生的缓冲力值越大,缓冲行程越小,为开展特性优化奠定了基础。
