基于变化速率的单变量报警系统设计

曲俊潇， 王建东， 王 振

(山东科技大学电气与自动化工程学院，青岛 266590)

报警系统是一种监视设备运行工况并提醒工作人员及时处理异常状况的系统，工业设备安全高效运行的首道保护层及核心组成[1-2]，其性能优劣至关重要，甚至直接关系到环境污染、产品质量、设备损失、经济效益甚至人员伤亡等问题[3-4]。对于性能较差的报警系统，极易存在报警延迟过长的问题，从而导致操作人员不能及时有效地处理关键报警信息。此外，不合理的报警系统可能会造成报警泛滥等问题，大大超出操作人员的处理能力。

现如今, 报警系统的性能优劣越来越受到工业界和学术界的关注[5-6]，EEMUA-191(工程设备和材料用户协会)指出了报警系统的意义和现状，同时对报警系统提出了许多要求和指标，是报警系统管理最重要的标准之一[7]。目前，报警系统常用滤波(filtering)、延时 (delay-timers)和死区(deadbands)三种方法来减少漏报率、误报率以提高报警系统性能。目前，国外学者对报警系统做了大量研究；Rothenberg对过程变量的噪声进行研究，将报警死区宽度设置为 20%的正常信号噪声[8]；Hugo[9]为了提高报警系统性能，设置了一种类似于卡尔曼滤波的自适应的报警死区；Hollifield等[10]指出在当代工业报警系统中，大部分报警死区都设置为零；Adnan等[11]使用马尔可夫过程计算报警死区和报警延时器的延迟时间，并设计了一种权衡误报率和漏报率以获得最佳配置的程序；Naghoosi等[12]估计报警抖动指数的方法以设计最佳报警参数；Xu等[13]提出了一种基于均值变化检测的新方法来估计误报率和漏报率的概率密度函数的报警延时器设计方法；Adnan等[14]使用马尔可夫过程计算误报率、漏报率和平均报警延迟，将广义报警延时器的性能和灵敏度与传统的报警延时器进行比较，并提出了广义报警延时器的概念及其性能指标计算和设计方法；Cheng等[15]在给出报警正常、异常数据统计分布情况下，设计了最优线性FIR报警滤波器；Zang等[16]采用了一种改进的延迟定时器触发和清除方法来提高报警系统性能，使用马尔科夫链计算改进后的性能指数；Tan等[17]在单变量报警系统中采用秩次滤波器(rank order filters)的方法，给出了报警系统性能指标的计算过程；Chen[18]提出了一种基于相关过程变量的变化方向的多变量报警系统设计方法；Afzal等[19]基于马尔科夫过程设计了报警死区，并推导出报警死区性能指标的解析表达式。

在中国，报警系统的研究也受到广泛关注。顾祥柏等[20]提出了基于物元的报警系统可拓重构，并通过基于关联函数的聚类算法简化其复杂性。赵劲松等[21]通过数据过滤优化了报警限的设计，大大减少了重复和无效报警。朱群雄[22]对报警系统的监控、优化设计和性能评估等方面的研究进行总结，指出未来报警系统的研究方向，并且通过可视化报警图解决报警泛滥的问题[23]。付蓉等[24]为控制输液速度和温度等信息，提出了一种基于输液速度与温度监控输液的设计。王佳等[25-26]利用时间序列的ARMA(自回归移动平均模型)模型和时间间隔的均方差模型设计了报警死区和报警延时器，并提出了一个基于模糊理论和数据挖掘算法得到的模糊加权关联规则挖掘算法用来快速识别报警根源。何乃翘等[27]通过报警系统评估关键指标得出报警系统操作员响应性能评价指标。朱群雄等[28]分析了造成报警泛滥的主要原因，总结了报警管理的研究进展。耿雪梅等[29]通过核密度估计法建立考虑人因指标的优化目标函数，设计得到一种报警阈值的自适应优化方法。陈斌等[30]通过多元回归分析建立了了眼动指标与疲劳的预测模型，通过瞳孔直径检测疲劳并报警。徐蕾等[31]提出一种识别人群异常行为的方法，通过人群分布和运动信息加以检测异常行为而更好的预警。龚安等[32]对单维状态数据通过时间序列自回归模型对主泵的异常状态进行检测。蔡郁等[33]提出了基于模糊推理和核密度估计来优化报警阈值的自适应调整方法。李俊杰等[34]通过区块匹配度的关联分析法解决报警泛滥问题。

对于传统的单变量报警系统而言，其监控对象是模拟信号的变化幅值，在设计报警死区和报警延时器来优化系统性能时，一般要求过程变量的正常和异常数据段统计分布已知且分布稳定。由于现代工业现场的需要，对变化速率较为平稳的信号可以对其速率进行监控。针对上述问题，提出了一种单变量速率变化的报警系统设计方法，首先通过基于时间序列的线性分段表示法，计算历史数据模拟信号的历史变化速率集合时间序列，其次判断历史变化速率集合分布是否稳定，然后确定变化速率的报警阈值，最后将在线运行的数据速率与速率报警阈值比较，从而判断过程信号是否发生异常，若发生异常则应触发报警，提醒操作人员进行处理。 本文关键技术是通过分段线性表示法对模拟信号进行分段减小噪声干扰和基于贝叶斯估计法判断历史变化速率集合的分布稳定性，如何对过程变量进行线性数据段的划分和如何判断分布稳定性是本文需要解决的主要重点和难点。

1 问题描述

在现代工业中，传统的报警系统报警方式如图 1所示，当过程信号超过上报警阈值或低于下报警阈值时，应触发报警，即报警信号xa=1；当信号低于上报警阈值且高于下报警阈值时，应消除报警，即报警信号xa=0。但传统的越限报警方式存在较多的缺点，如监控幅值变化受噪声干扰较大、报警延迟时间较长、误报警和漏报警较多等，通常会利用报警死区、滤波器和报警延时器等方法来解决报警泛滥等问题。但对于变化速率较平稳的变量，监测信号幅值的变化往往不能及时发现系统的异常状态，并且可能会因噪声的干扰而导致误报警过多等问题，会浪费大量的人力物力财力，严重时会导致重大事故的发生。

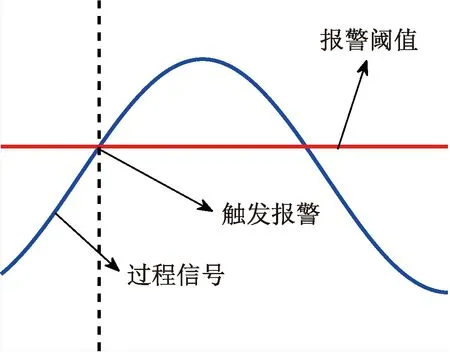
图1 传统报警方式示意图Fig.1 Schematic diagram of traditional alarm mode

由于现有的方法并未解决如何判断所选取的历史数据分布不再发生变化，导致通过历史数据所计算的报警系统参数不一定正确；并且对于未发生过报警的变量，无法获得该变量的异常数据段。针对变化较为平稳的变量，根据监测信号的变化速率设计一种新的报警系统，通过稳定的分布来确定报警系统的参数，以此来提高报警系统的性能。 对于较为平稳的信号如图2所示，由于存在噪声干扰，传统的报警系统仅监控模拟信号的幅值变化，其方式较为单一；并且极易产生误报警和漏报警，会存在较长时间的报警延迟。

图2 平稳信号的噪声干扰Fig.2 Noise interference of stationary signal

研究最终的目的是设计一种基于变化速率的单变量报警系统，具体需要解决的问题如下：①根据数据分布的稳定性确定选取历史数据的数量并计算速率报警阈值；②计算模拟信号的变化速率，并判断速率报警器应何时触发报警。

2 主要方法

主要方法是根据有限的历史数据，利用基于贝叶斯估计的方法，判断过程变量的历史速率集合的分布稳定性，并通过稳定的速率集合计算速率报警阈值。利用等长时间窗口，对窗口内的数据进行线性分段表示，计算窗口内数据的最小二乘拟合结果及斜率的置信区间，并与速率报警阈值相比较，判断信号的速率变化是否超出正常的速率变化范围。在当前窗口内的数据完成计算后，将时间窗口滑动一个采样时间，以达到在线监测过程信号速率变化是否异常的目的。

2.1 训练数据确定参数

对于速率报警器而言，首先应判断待测变量的正常运行状态下历史数据所获得的历史变化速率集合分布是否稳定，即速率样本的统计分布是否不再改变，然后通过稳定的速率集合确定信号的速率报警阈值。

2.1.1 历史数据计算斜率

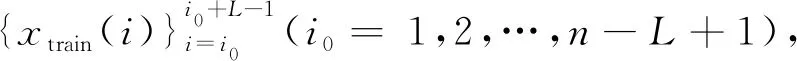
(1)

故式(1)经过计算，解得系数为

(2)

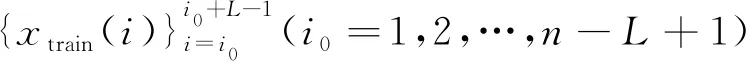
(3)

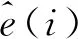
(4)

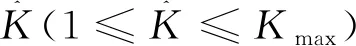
(5)

式(5)中：NR为数据个数；σ2为拟合误差。

(6)

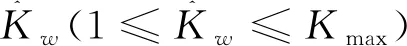
(7)

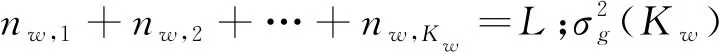
(8)

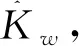
(9)

Kmax可由操作人员视情况确定。

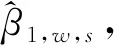
2.1.2 确定速率报警阈值

通过正常状况下历史数据{xtrain}得到的历史速率集合{ktrain}，记Ktrain:={ktrain}，数据长度为nk。将{ktrain}的最大值和最小值等长度间隔分为B个小区间，设第b(1≤b≤B)个小区间内包含m个数据，这里通过贝叶斯估计法来估计每个小区间的组频率概率密度，获得组频率的置信区间。此处假设先验分布为均匀分布。

设第b个区间的组频率为

(10)

且fb～U(0,1)，即离散概率密度函数为

(11)

式(11)中：M为离散点的个数。则历史速率集合{ktrain}在fb的条件分布下，似然函数为

(12)

故联合分布的概率密度函数为

pKtrain,Fb=pKtrain|Fb(k|fb)pFb(fb)

(13)

所以，在k=m时，根据贝叶斯公式，后验分布的概率密度函数为

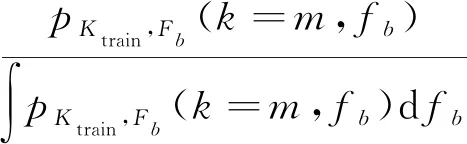
(14)

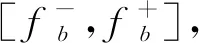
(15)

定义组频率稳定指标：

(16)

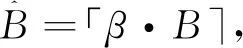
选取稳定分布S0的99.5%和0.5%分位数ktp,H、ktp,L作为速率报警阈值，以确保速率报警器的误报率不超过1%。

2.2 在线运行

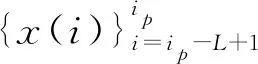
步骤1通过式(7)，计算窗口w内最优分段数损失函数，并根据式(9)求出窗口内数据的最优分段数，将窗口w内第q段分段结果用式(3)线性模型表示：

(17)

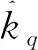
(18)

(19)

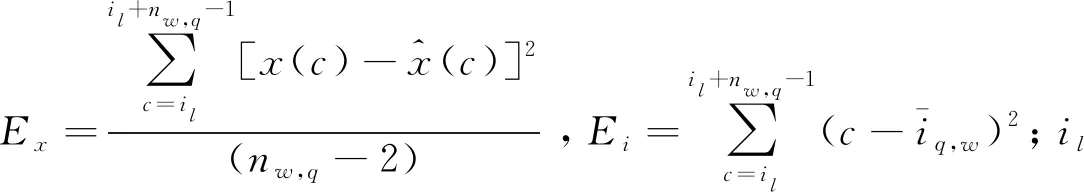
步骤3定义报警信号为xa，当系统未发生异常时，xa=0；当系统发生异常时，xa=1。在速率报警器中表示为

(20)

3 现有方法

Savitzky-Golay滤波器[40]是一种常用的滤波算法，广泛应用于工业中数据的降噪处理。Savitzky-Golay滤波的效果随着选取窗宽和拟合阶次的变化而有所差异，可以满足多种场合的需求。设滤波窗口的宽度为G，各测量点为窗口中心点，即xf={x-(G-1)/2,x-(G-1)/2+1,…,x-1,x0,x1,…,x(G-1)/2-1,x(G-1)/2}，采用mf次多项式对窗口内的数据点进行拟合，每一个点可以表示为不同的多项式的结果，设：

进而得到方程组的最小二乘解估计值

(21)

式(21)中：Xf=[x(i-(G-1)/2),x(i-(G-2)/2+1),…,x(i0),…,x(i(G-1)/2-1),x(i(G-1)/2)]T。将信号经过S-G滤波处理后，应用于报警系统中，减小噪声的干扰，以此来提高报警系统的性能。

4 方法验证

通过仿真案例和工业案例，对所提出的速率报警器进行验证，通过与传统的报警系统相比较，证明了所提出方法的准确性，并验证了判断数据分布稳定方法的有效性。

4.1 仿真案例

首先通过仿真数据验证基于贝叶斯估计判断分布稳定性方法的准确性，再利用仿真案例，对比速率报警器与经过S-G滤波的报警系统，以此来说明速率报警器的准确性。

构造数据过程如下：

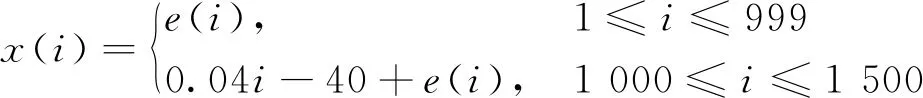
(22)

式(22)中，e(i)服从高斯分布，即e(i)～N(0,1)。系统在i=1 000时发生异常，应触发报警。这里，假设该信号的高报警阈值xtp=5。根据正常数据段获得速率集合{ktrain}，且S0={ktrain}。

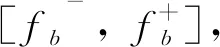
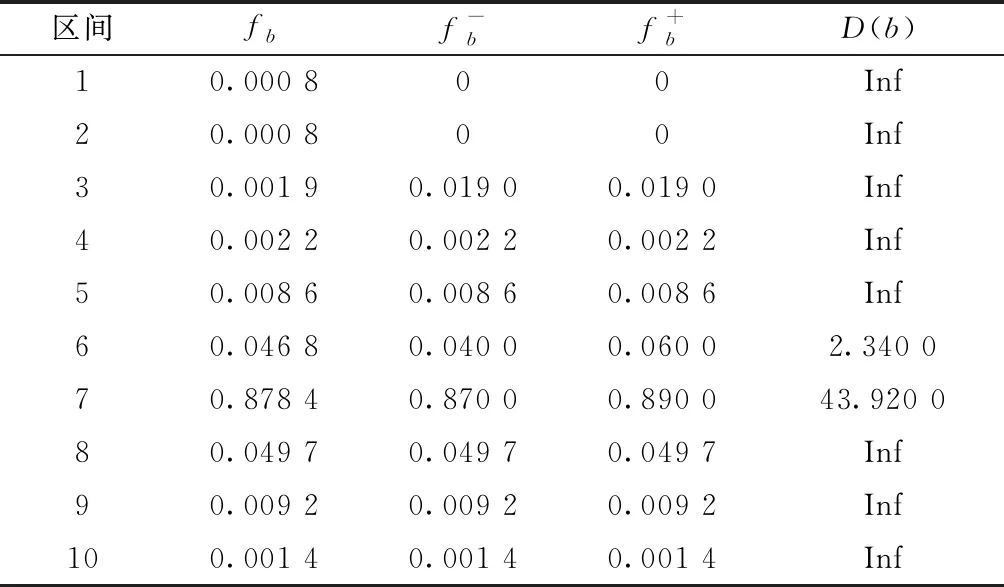
表1 稳定分布组频率及置信区间

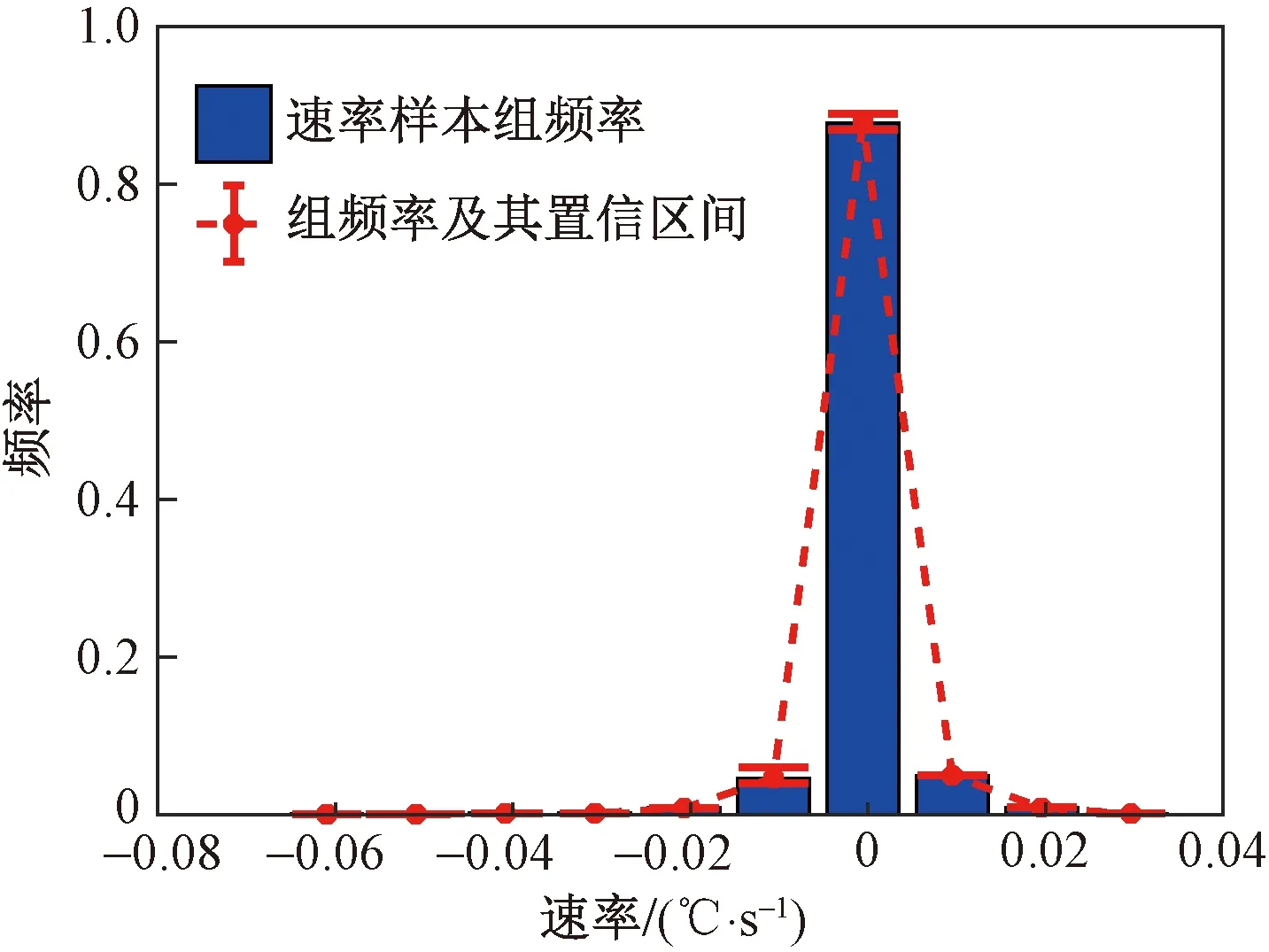
图3 仿真案例稳定速率分布的组频率及其置信区间Fig.3 The group frequency and confidence interval of steady rate distribution of simulation case

继续增加样本nadd得到样本SN，SN的组频率与分布S0所得置信区间展示在图4中。表2给出SN组频率，并计算得出SN的第6～8个区间的组频率在S0的置信区间内。分布SN的组频率在分布S0所得置信区间内的概率密度函数面积AN=97.55%，AN>β。

表2 SN的组频率

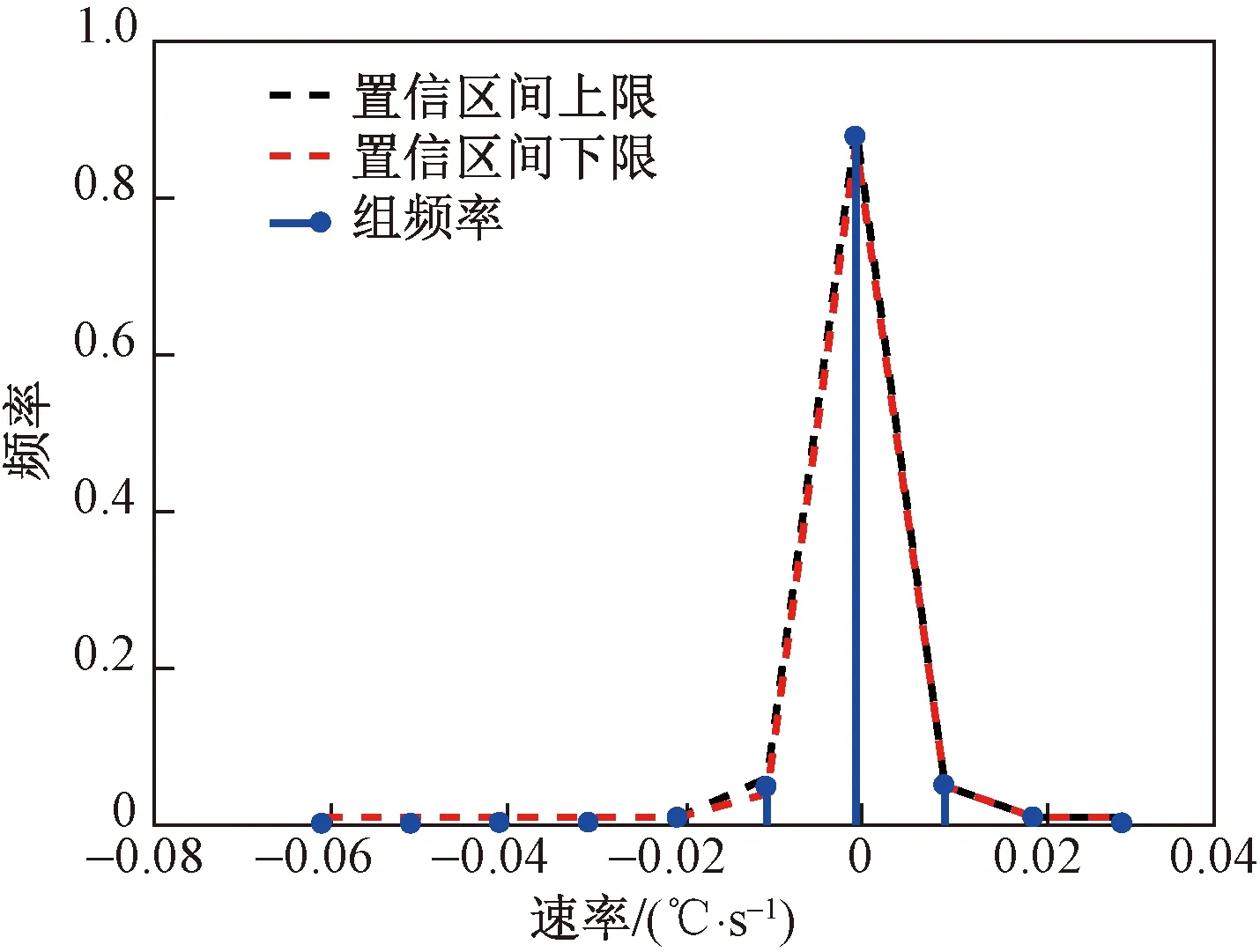
图4 仿真案例S0置信区间与SN组频率Fig.4 S0 confidence interval and group SN frequency of simulation case

图5 仿真案例稳定速率分布Fig.5 The simulation case stabilizes the rate distribution

计算所得的仿真案例结果如图6所示，其中图6(a)为速率报警器触发报警时所识别出的数据，图6(b)为速率报警器检测速率信号不在正常范围时触发的报警信号，所以速率报警器的报警延迟时间为60 s。

图6 速率报警器仿真案例结果Fig.6 Simulation results of rate alarm

根据第3节中S-G滤波器[40]，通过式(21)得出滤波后的信号如图7所示。最终，仿真结果得出传统报警系统的报警延迟时间为113 s。

图7 S-G滤波器仿真案例结果Fig.7 Simulation results of S-G filter

比较两种方法得出结论，速率报警器结果准确，受噪声干扰较小，能及时检测出信号的异常状态，且报警延迟时间明显小于S-G滤波器，整体性能更优。

4.2 工业案例

选取莱城电厂#4机组2015年6月15日8:30—15:10“C磨非驱动端轴承温度1”信号进行工业数据验证，该信号规定的报警阈值上限为51。经过第3节所介绍的S-G滤波器计算，得到滤波后的过程信号及报警信号如图8所示，图8(a)表示过程信号，图8(b)表示报警信号xa，当xa=1时，传统报警系统检测到异常状态，触发报警。

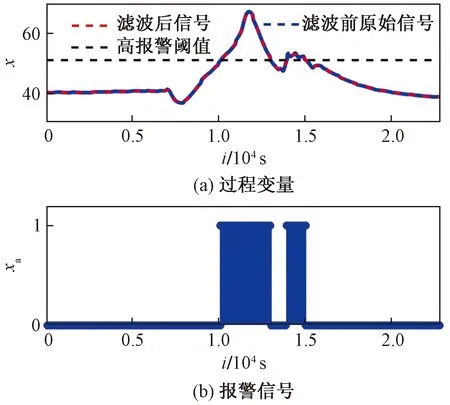
图8 “C磨非驱动端轴承温度1”S-G滤波工业案例结果Fig.8 “C-mill non-driving end bearing temperature 1” S-G filter industrial case result

速率报警器的离线计算部分中，根据子节2.1.2中判断分布稳定性的方法，稳定分布的组频率及其置信区间上下限如图9所示，其中红色区间表示历史速率稳定分布的组频率置信区间。

图9 工业案例稳定速率分布的组频率及其置信区间Fig.9 Group frequency and confidence interval of steady rate distribution in industrial cases

根据式(16)计算组频率稳定指数，得到分布SN的组频率与分布S0所得置信区间如图10所示，计算所得其面积AN>β。

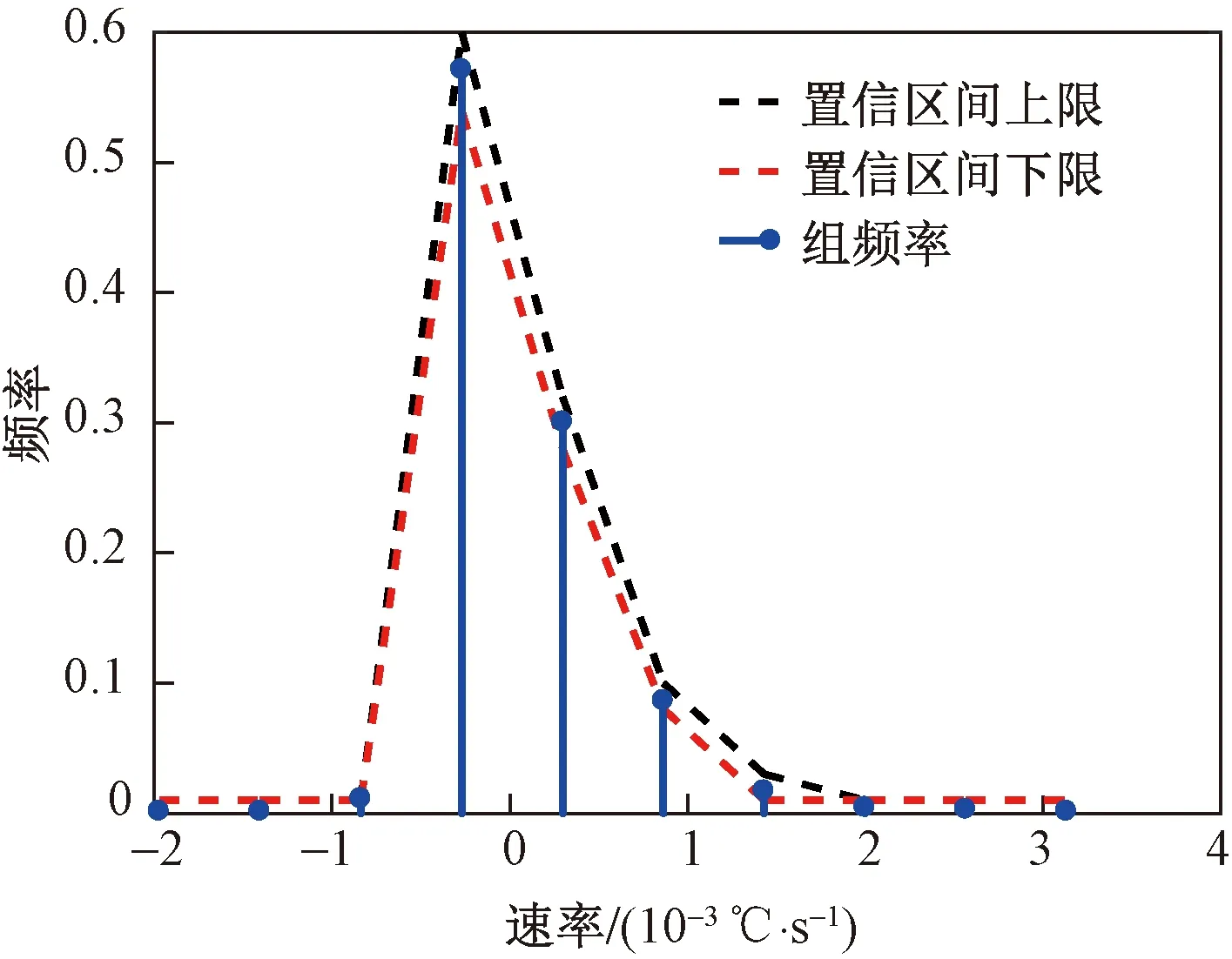
图10 工业案例S0置信区间与SN组频率Fig.10 Industrial case S0 confidence interval and group frequency of SN

最终得到的稳定分布S0的概率密度曲线则如图11所示。选取稳定速率分布S0的0.5%和99.5%分位数作为速率报警阈值，分别为ktp,L=-0.002 2、ktp,H=0.003 0，继而进行速率报警器的在线运行。

图11 工业案例稳定速率分布Fig.11 Steady rate distribution of industrial cases

图12分别为温度信号和速率报警器所触发的报警信号，其中在图12(a)中，红色实线表示速率变化异常部分，在图12(b)中，蓝色针状图则表示信号速率变化超出正常范围时所触发的报警信号。

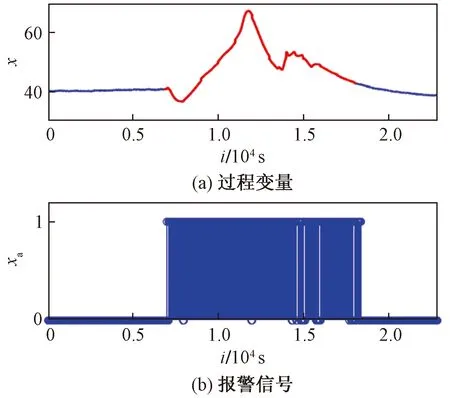
图12 “C磨非驱动端轴承温度1”速率报警器仿真结果Fig.12 Simulation results of “C mill non-driving end bearing temperature 1” rate alarm

图13表示所得到的信号变化速率，其中红色虚线为速率报警阈值的上下限。根据图13 能明显地看出信号速率的变化与磨煤机轴承温度信号的变化趋势大致相同，并且由于引入速率信号置信区间的计算，大大降低了速率报警器的误报率。

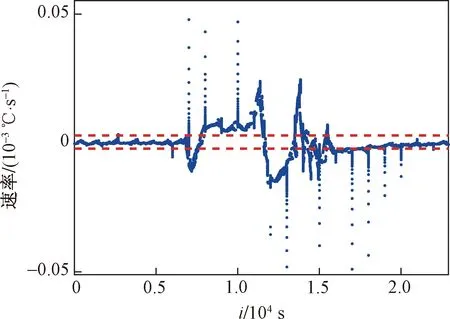
图13 “C磨非驱动端轴承温度1”的速率信号Fig.13 Slope of “C mill non-driving end bearing temperature 1”

根据工业案例的结果可知，速率报警器在i=7 110 s时触发报警，比传统的报警系统在i=10 124 s时触发报警提前了3 014 s，并且误报率明显低于1%，其性能要优于传统的报警系统。

5 结论

提出了一种基于速率变化的报警器，该报警装置作为一个新型的报警装置，通过贝叶斯估计判断历史数据所获得的速率集合分布稳定，当组频率基本稳定时，则分布稳定。根据分布稳定的数据分位数，可以获取速率报警阈值的上下限，并通过滑动窗口法选取数据，利用自底向上法计算信号变化速率，当系统在线运行时，计算窗口内信号速率的置信区间并与报警阈值相比较，判断系统是否发生异常。最后根据仿真结果和工业案例得出结论：速率报警器不再局限于传统报警系统只监测模拟信号幅值变化的模式，对信号速率的变化进行监控，尤其对于速率变化较为平稳的信号，速率报警器的性能要明显优于传统报警系统，并且可以得到信号变化趋势，对于操作人员判断发生异常的原因有着重要的意义。