关于接触压力影响RF类连接器接触电阻测试精度的问题分析①

杨静静，孙杰明

(中航富士达科技股份有限公司泰斯特实验室，西安 710077)

0 引言

接触电阻是电连接器电性能参数的重要指标，通过测试接触电阻，不仅可以反映各种电接触形式的稳定性，而且还可以反映微型电子元器件在复杂环境条件下使用时的形变情况等[1，2]，但由于其阻值的特殊性，在进行接触电阻测试时产生的误差往往会对最后的结果产生较大的影响，只有明确误差的来源，才可在试验中有效的避免或使误差最小化，这样最终的测试数据才更具真实性[3，4]。

1 接触电阻的测试原理

由于接触电阻阻值的数量级较小，所以在进行测试时，首先要保证的是，测试设备可以有效的消除自身带有的误差，例如，对于射频同轴连接器而言其接触电阻阻值可以是10-2～10-4数量级，因此如果不消除设备自身的测试误差,那么对于小电阻测量而言，是无法保证测试结果的真实性的，那么对于小电阻测试而言，其测试原理可用图1表示：

图1 接触电阻测试原理图Fig.1 Principle of Contact Resistance Testing

其实开尔文电桥是惠斯通电桥的升级和变形，其中R1、R2、R3、R4均为可变电阻，RX为被测低电阻，Rn为低值标准电阻与惠斯通单电桥对比，开尔文电桥做了两点重要改进：

(1)增加了一个由R2、R4组成的桥臂。

(2)RX和Rn由两端接法改为四端接法。其中P1P2构成被测低电组RX，P3P4是标准低电阻Rn，P1P2、P3P4为电压接点，C1C2、C3C4称为电流接点。从图中可以看出，采用卡尔文四线桥法时，将RX电流端电阻和Rn电流端的电阻RX与，接入电源回路，从而消除了这两端的电阻对电桥电路的影响[2]，其次在RX和Rn电压端的电阻又分别于先对大电阻R1、R2、R3、R4串联后，在RX和Rn电压端的电阻几乎没有分压作用，因此消除了电压端电阻对电桥电路测量结果的影响，而RX和Rn端的连线电阻则r可以通过对R1、R2、R3、R4，的调节消除r对测量结果的影响，当当电桥电路中检流计实数为零时则有以下RX为：调节R1、R2、R3、R4使电桥平衡。此时，Ig=0，I1=I3，I2=I4，I5=I6，VB=VD，且有

I3R3=I4R4+I5Rx

(1)

I1R1=I2R2+I6Rn

(2)

I2R2+I4R4=(I5-I4)R′

(3)

三式联立求解得

(4)

如果平衡等式中满足如下条件；

(5)

则以上等式则可化简为：

(6)

在实际的测量中，如(5)式中所表示的关系受到设备或者人为操作的影响难以达到，只能近似相等，所以在测试过程中RX和Rn的引线电阻R要尽可能的小，所以在RX和Rn直接的连接导线尽可能采用横截面积较大且较短的导线连接而：R1R4=R2R3和R′≈0的设定，消除了附加电阻的影响，从而保证了测量低电阻时的准确度。

2 接触压力对测试的影响

由于在实际的测试过程中，影响接触电阻测试的因素很多，本文中以测试时的正压力为例，采用最小二乘法对接触电阻的测试进行分析[5]，由于不同的接触形式对小电阻的测试也会带来较大的影响，因此提出以下猜想；如压力增大，接触面的接触点和接触面积也会增大，最终接触点从弹性变形转化为塑性变形[3]，这种塑性变形会使集中电阻减小，从而接触电阻降低[4]，证明如下：

首先采用图2的方式测得以下数据。

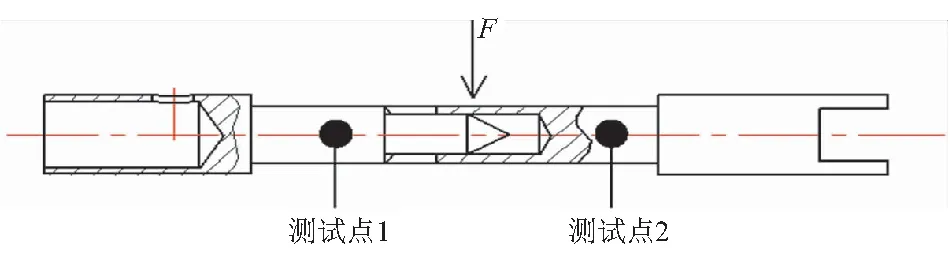
图2 接触关系图Fig.2 Contact Relationship

从表1的数据可知，在正压力增大时，接触电阻阻值在不断减小，因此将这种变化表示为以下关系如图3所示。

表1 接触电阻与正压力的关系Table 1 The Relationship Between Force and Resistance

图3 正压力与接触电阻的变化趋势Fig.3 Trends in Pressure and Resistance

从图3可观察到，正压力与接触电阻的变化趋势类似于一条直线，因此假设接触电阻与正压力的关系为：

f(x)=ax+b

(7)

将表1的数据带入上述表达式可得：以下方程组(8)

10a+b-1.164=0

11a+b-1.160=0

12a+b-1.153=0

13a+b-1.154=0

14a+b-1.150=0

16a+b-1.144=0

15a+b-1.146=0

(8)

根据上述方程组，试图找到一个a，b；使得上述7个等式分别成立，但是根据一元一次方程的概念，这是不可能的，任何a，b带入上面都会产生一定的误差[5]，但是，可以找到一个a，b带入上式使得各等式之间误差最小，因为纯代数运算的关系，只需要使各等式的平方误差最小即可,因此可将上述的具体问题转化为下列方程组：

(9)

(10)

(11)

则所求的最小二乘解可以表示为求：向量|Y-B|2最小值，即要求向量Y-B的膜最小，在欧式空间中一个固定向量到子空间的向量的距离也是以“垂线最短”所以将上述矩阵写为：

(12)

令A的各列向量为(a1，a2，a3…as)，由列向量生成的子空间为L(a1，a2，a3…as)，那么就是A中向量，则Y也是子空间L(a1，a2，a3…as)的向量。因此向量到子空间的距离可以表示为在子空间L(a1，a2，a3…as)中找一个向量Y，使得向量B到它的距离比其到子空间中L(a1，a2，a3…as)其他向量的距离都短，则猜想可以得到证明，由上式可知

Y=AX=a1x1+a2x2+…asxs

是所求的向量，则距离可表示为：

C=B-Y即C=B-AX

由于向量B垂直于子空间L(a1，a2，a3…as)，则必然有以下联系：

Ca1+Ca2+Ca3…Cas…Cas=0，

即(C，a1)=0，(C，a2)=0，…(C，as)=0

然后用矩阵数乘关系可以得出为：

AT(B-AX)=0⟹ATB-ATAX=0

即：ATB=ATAX、(13)

由此X的解析式，可以看出ATB为常数项而ATA为系数矩阵，所以式中的X总是有解的，到此，最小二乘法有解的充要条件得到证明，所以带入之前的所提出的问题中则有：

(14)

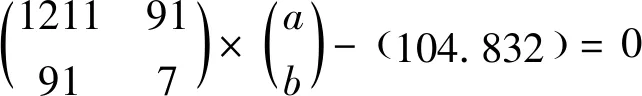
(15)

得

即，a=-0.00325，b=1.1952

由此可以得出一个关于正压力与接触电阻阻值的关系式如下：

R=-0.00235X+1.1952

(17)

将测试与计算的结果进行拟合，曲线见下图4所示：

图4 拟合曲线图Fig.4 Fitting Curve

根据拟合曲线的确定，证明最初的假设成立。

3 结论

综上所述，影响电连接器接触电阻测试的原因很多，如果仔细分析每一种因素对测试结果的影响是不现实的，但是如果将这些因素进行整理和归纳，无外乎二种因素，一是测试原理的不同，二是接触方式的不同，究其原理而言，测试方法不同但是基础并没有什么区别，其根本就是为了尽可能的降低系统测试带来的误差，在进行RF连接器接触电阻测试时，接触压力的不同，究其本质也是改变了产品原有自然状态下得接触方式，进而对最后的测试结果产生较大的误差。并且这种误差会随着接触部位压力的增大而呈现正比例变化，因此在进行工程毫欧级接触电阻测试时，应采用自然插合的接触方式进行测量，同时应避免人为产生的接触压力，导致自然插合状态的改变。才可能真正做到消除或者减小试验误差，从而保证试验结论的真实有效。