四旋翼无人机PDF控制系统设计和抗干扰分析

尹 豪,唐 猛, 侯 凡

(西南交通大学 机械工程学院，成都 610031)

0 引言

四旋翼无人机是当下比较热门的一种多旋翼无人机，目前已被大量应用于航拍，侦察，巡线，喷洒农药等众多领域。而常用的PID控制方法具有结构比较简单，其参数调整也相对方便的特点，故在四旋翼无人机控制的工程实际应用中技术人员一般都采用PID控制策略。但在某些特定的高精度控制和抗扰动应用场合，常用的PID控制算法往往不能满足需求。为了能够适应这些应用对四旋翼无人机控制性能的特定需求，在国内外都出现了多种更智能的控制方法应用在四旋翼无人机中的研究，比如：模糊PID控制[1]、自抗扰飞行控制[2]、滑膜控制[3]以及多种控制方法的结合等等。这些控制器相对于PID控制器的控制效果都比较好，但这些控制器的结构也更加复杂，以及建立它们的数学模型变得困难，不利于四旋翼无人机的实际控制应用[4]。

伪微分反馈(Pseudo Derivative Feedback)控制策略[5]，简称为PDF控制，是由美国纽约州康奈尔大学的Phelan教授于1977年在其书籍《Automatic Control Systems》中提出的，是一种基于One-Master原则的实用性很强的控制架构。以往许多的研究表明，PDF策略相比PID控制策略具有更强的鲁棒性、较强的抗干扰能力和好的动态控制性能。本文就主要工作就是研究将伪微分反馈控制方法引入到四旋翼无人机中，以提高其控制性能；通过建立PID和PDF姿态控制器的控制仿真模型，研究PDF和PID策略在阶跃输入和外部干扰下的的性能提升。

1 四旋翼无人机动力学模型

1.1 坐标系建立及坐标系变换

四旋翼无人机的旋翼结构布局常用的有十型结构和X型结构，本文的四旋翼机型采用X型，它的4个旋翼(1、2、3、4)分别位于X型结构的前后左右4个端点上，分为正对角线和反对角线两组，且飞行时两组旋翼的旋转方向刚好相反。即电机1和3逆时针旋转，电机2和4顺时针旋转，四旋翼无人机结构如图1所示。

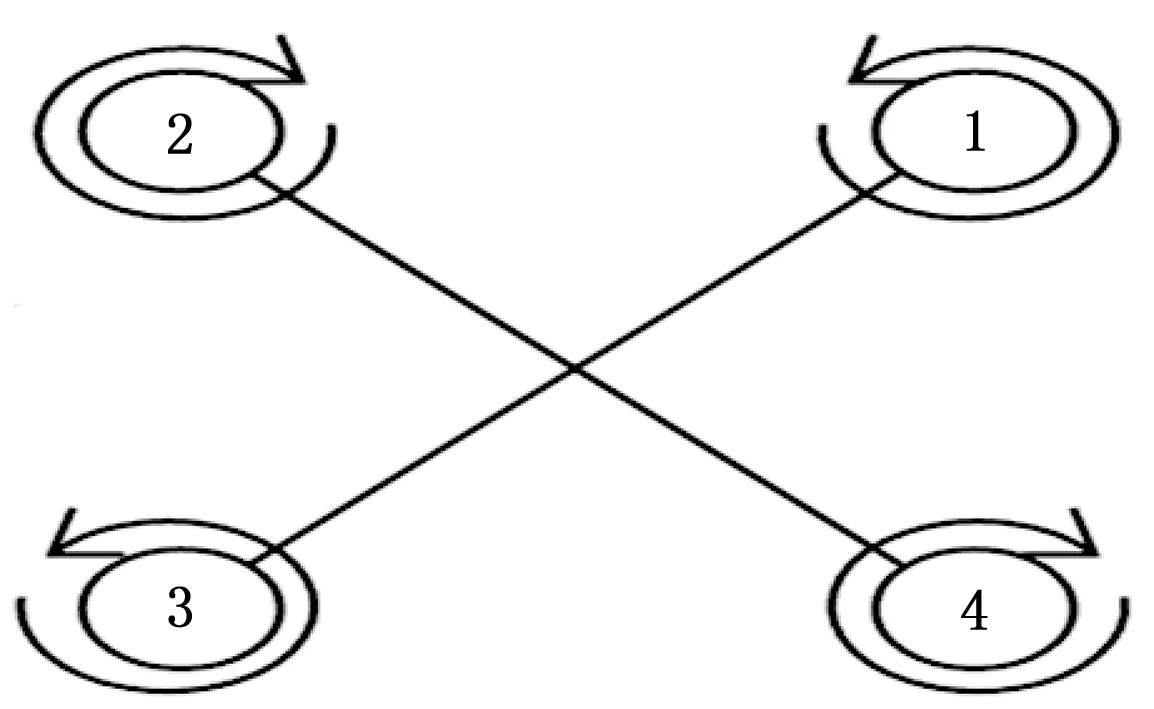
图1 四旋翼无人机结构简图

为描述四旋翼无人机的运动学关系，本文为此建立了两个坐标系，分别为地面坐标系与以无人机重心为原点的机体坐标系。其中地面坐标系是用来表示四旋翼无人机在整个地球空间的三维位置坐标XN、YN、ZN，以便观察飞行器相对于地面的运动状态，由此可以得到四旋翼无人机的航向、姿态和位置信息。地面坐标系示意图如图2所示，规定坐标原点与四旋翼无人机的起飞点重合，沿飞行器的前进方向为ONYN正轴，垂直于水平面向上为ONZN正轴，垂直于ONXNZN平面向上为ONYN正轴，其与轴ONXN、轴ONZN构成右手坐标系。

本文机体坐标系的定义如下：机体坐标系的选择在以下几个前提的假设下，不管飞行器高度如何变化，重力加速度是不会变的，也即四旋翼无人机的重量是不会变的；无人机的结构保持稳定，使得它的重心要保持不变；且飞行器是刚体，因此不会发生弹性形变。该坐标系是一直附着在机体上的，其原点位于四旋翼无人机的重心位置，OBXB轴与无刷直流电机1和2的对称线平行，假定向前为正；无刷直流电机2和3的对称线即为机体坐标系的OBYB轴 ，假定向左为正；而机体坐标系的OBZB假定向上为正，符合右手坐标系的规定。

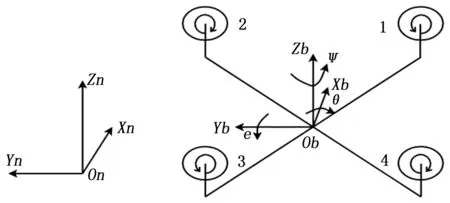
图2 地面坐标系与机体坐标系示意图

由于四旋翼无人机具有特殊的结构，使得仅通过调整4个旋翼的转速，就可以改变它的飞行姿态。对于四旋翼的各种姿态控制有以下几种情况：1)四只旋翼的旋转速度恒定并相等，而且它们的升力之和等于四旋翼的重力，此时无人机处于悬停状态；2)旋翼1和4的转速增大，而旋翼2和3的转速减小(或者旋翼1和4的转速减小，而旋翼2和3的转速增大)，此时无人机做滚转运动；3)旋翼1和2的转速增大，而旋翼3和4的转速减小(或者旋翼1和2的转速减小，而旋翼3和4的转速增大)，此时无人机做俯仰运动；4)旋转方向相同的一组旋翼转速增大(或减小)，而另一组旋转方向相反的旋翼转速减小(或增大)，此时无人机做偏航运动。为方便描述四旋翼无人机的姿态，本文将3个欧拉角分别定义如下：滚动角φ为机体轴ZB与地面坐标系中XNONZN平面之间的夹角，假定飞行器向右滚动角度为正；俯仰角θ为机体轴XB与地面坐标系中XNONYN平面之间的夹角，假定飞行器低头时为正；偏航角ψ为机体轴XB在水平面上的投影与地面坐标系XN轴之间的夹角，假定飞行器机头向左偏航时为正。

由欧拉角定义可知，从机体坐标系到地面坐标系的位置变换，可以通过绕不同机体坐标轴的三次连续转动来实现。因此，将四旋翼飞行器的机体坐标系依次绕ZB轴，YB轴，XB轴(即Z-Y-X顺序)旋转三次可以转换到地球坐标系，机体坐标系到地面坐标系的旋转矩阵为：

(1)

其中：c代表cos函数，而s代表sin函数。

1.2 动力学模型的建立

四旋翼无人机，顾名思义就是它具有4个旋翼，每个旋翼由一个无刷电机驱动旋转，而4个旋翼一共需要4个无刷电机驱动，这4个无刷电机即为系统的动力输入。而四旋翼无人机在三维空间有6个自由度，6个自由度仅有4个动力输入，所以它是一个欠驱动系统。而且它的姿态角度与水平位置之间具有较强的耦合关系，故四旋翼无人机是一个强耦合、欠驱动的非线性系统。本文采用牛顿-欧拉公式推导四旋翼无人机的动力学方程，由于它的运动学和动力学系统是非常复杂的，想要完全准确的建立系统的数学模型极其困难。本文为了方便的研究对象，将无人机的动力模型简化，建立一个相对准确的模型，提出以下假设[6]：

1)把飞行器视为一个刚体，忽略它的弹性变形；

2)把地面坐标系视为惯性坐标系，以忽略地球自转与公转对飞行器的影响；

3)飞行器的飞行领域内，重力加速度保持不变；

4)无人机的形状与质量关于它的中心都是X型对称的；

5)忽略它在飞行中所受到的空气阻力；

6)四旋翼无人机在低速的，小角度情况下飞行。

在上面假设的情况下，四旋翼无人机所受合外力主要由飞行器本身的重力和4个旋翼旋转所产生的升力和某些外部干扰力(比如风力)组成。飞行器受到的升力与4个旋翼的旋转速度的平方是正比关系，记4个旋翼的转速分别为Ωi(下标i的取值为1,2,3,4)，则

(2)

其中，kF为旋翼升力系数。

四旋翼在地面坐标系下受到的合力为：

(3)

其中:Fx、Fy、Fz为XN、YN、ZN轴所受合力，fx、fy、fz为XN、YN、ZN轴的扰动。由牛顿第二定律得：

(4)

由于四旋翼无人机的结构布局是均匀对称的，故Jxy、Jyz和Jzx都等于零，可知机体的转动惯量矩阵为对称矩阵，即

(5)

其中，Jx、Jy、Jz为无人机绕机体坐标系XB、YB、ZB轴旋转的转动惯量。

则由欧拉方程可得

(6)

其中Mx、My、Mz为绕机体坐标系三轴所受力矩，p、q、r为绕机体坐标系三轴转动的角速度。

进一步对转动力矩进行分析：

(7)

其中:L为旋翼中心与机体重心之间的距离，kM为旋翼反扭矩系数。

将式(7)代入式(6)得

(8)

机体角速度与欧拉角速度对应关系：

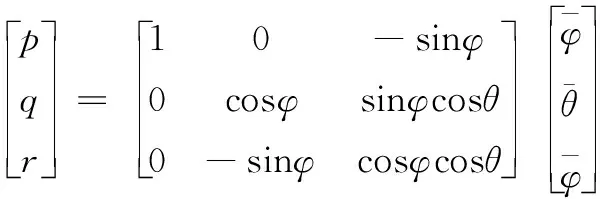
(9)

本文研究的情况为四旋翼无人机小角度、低速飞行，因此可以做如下近似：

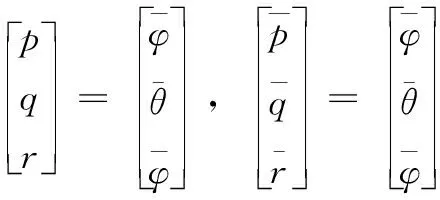
(10)

将式(10)代入式(8)整理得

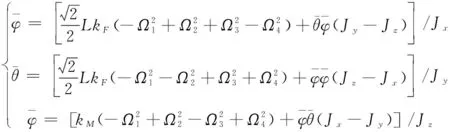
(11)

为简化系统数学模型，令

(12)

它们为四旋翼无人机4个独立通道的控制量，U1、U2、U3、U4分别为垂直升降、滚动力矩、俯仰力矩、偏航力矩控制量。四旋翼无人机飞行器的动力学最终模型为：

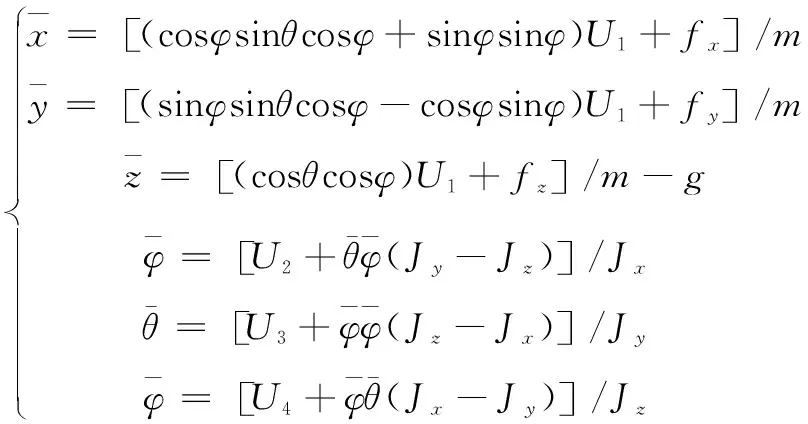
(13)

2 无人机PDF姿态控制器设计

2.1 PDF控制策略

PDF控制器的架构类似PI控制器，但是目标值和反馈的误差只作为I(积分)控制器的输入，误差不是P(比例)控制器的输入，改用反馈作为P(比例)控制器的输入，因为误差不是比例控制器的输入，因此也被Phelan称之为伪微分反馈(PDF)[7]。

图3 二阶PDF策略控制器结构

由公式(13)可知，四旋翼无人机的姿态控制模型是一个二阶控制系统。PDF策略的二阶控制结构如图3所示，整个系统的末级控制元件由传递函数1代表，其物理元件的最大能量输出决定了输出最大值M2的取值[8]，Ki、Kd1和Kd2都为PDF控制系统的系数。

2.2 PDF控制器系数确定

本研究对象模型参数如表1所示。

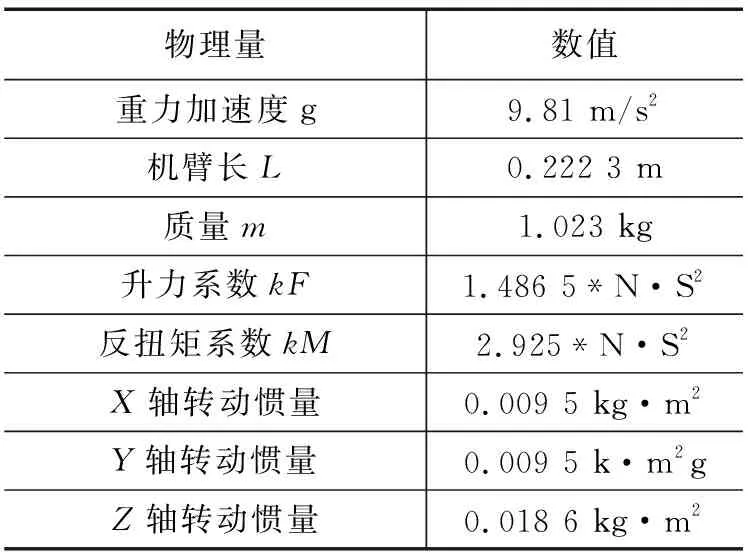
表1 四旋翼模型参数

由文献[9]可知，对于一个二阶对象来说，PDF控制系数的设定公式如下：

Ki=6.52·[Mmax/(I·r0)]1.5

(14)

Kd1=8.53·Mmax/(I·r0)

(15)

Kd2=4.13·[Mmax/(I·r0)]0.5

(16)

式中，I为被控对象的最大阶项系数，r0为系统的阶跃参考输入的最大值，Mmax为末级控制元件的最大输出值。由式(13)可知，I等于机体轴转动惯量，r0=30*pi/180，末级控制元件最大输出为滚动、俯仰和偏航最大瞬时力矩乘以对应的机体轴转动惯量，最大力矩为2.5 N·m，3个PDF姿态控制器的系数如表2所示。

表2 四旋翼PDF控制器参数

2.3 四旋翼仿真模型

由式(13)可知，四旋翼无人机的3个姿态控制量具有耦合关系。但在较小的姿态角速率情况下，可以忽略它们相互间的耦合影响，由此可以按照单通道控制系统分别设计。Matlab/Simulink软件平台具有强大的仿真功能，可以在此平台上对四旋翼的动力学模型进行动态仿真。本文对滚动、俯仰、偏航3个通道分别独立进行PID和PDF控制仿真，整个系统的Simulink仿真模型如图4所示。

在图4中，仿真模型的构成主要有四部分：姿态信号模块、控制器、控制量转换和四旋翼无人机动力学模型。其中姿态信号模块包括姿态角命令信号和反馈信号。姿态控制器采用PID和PDF控制器，其输入为欧拉角命令值和反馈值，输出为U1、U2、U3、U4。姿态控制器的输出是中间控制量，这些量的实现最终都是靠四旋翼无人机的4个电机实现的，要达到这些控制，每个电机的具体值可有前面的式(12)反推得到。四旋翼无人机动力学模型通过一个level-2 MATLAB S-Function来实现。四旋翼PID控制器仿真模型和PDF控制大致结构类似，只是把PDF控制器换成里Simulink自带的PID Controller模块。

3 控制及仿真结果

下面通过如下几个方面进行控制性能仿真，从而从仿真的角度评估PDF算法在四旋翼姿态的动态响应及抗干扰的优越性。

3.1 PID和PDF在阶跃输入的输出响应

3个姿态角Φ、θ、ψ的初始值都是0，最终输出分别是10*pi/180rad、20*pi/180rad和30*pi/180rad，阶跃时间点分别是4 s、7 s和10 s。滚动角Φ、俯仰角θ和偏航角ψ的PID和PDF控制输出仿真如图5所示。

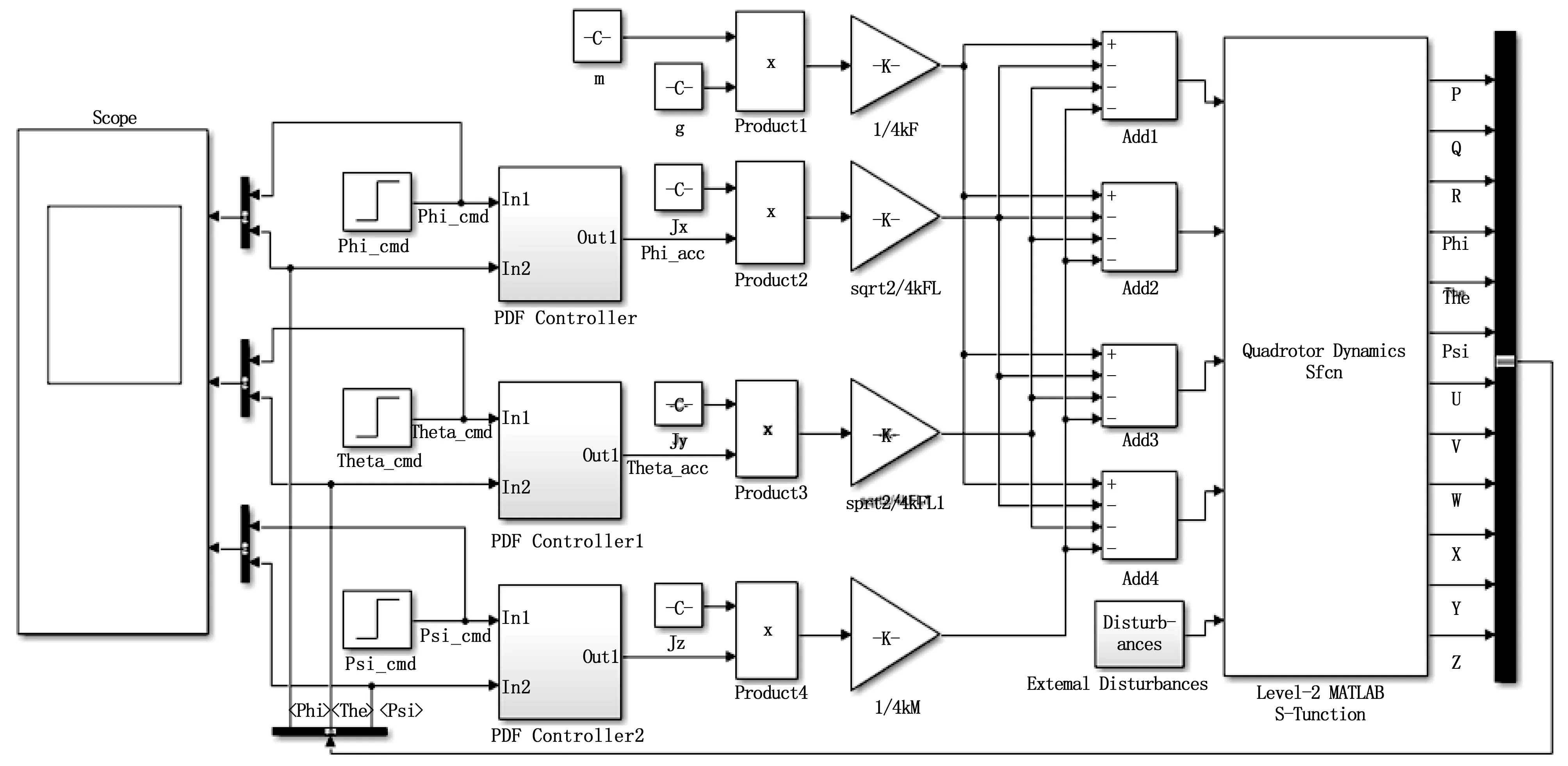
图4 四旋翼基于PDF控制的仿真模型

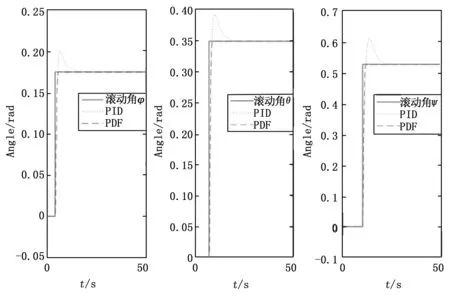
图5 PID和PDF控制下的姿态角曲线

在没有外部扰动作用时，加上积分环节控制会导致系统的动态性能变差，而当有变化的外部扰动作用时，积分控制又不能很好的发挥它对干扰的抑制作用。因此，在对四旋翼无人机的Simulink模型进行基于PID姿态控制和抗干扰控制模拟仿真时，本文主要利用比例环节和微分环节对姿态进行控制[10]。基于PID控制算法的调试主要是利用试凑法整定PID算法的各个参数，通过先比例、后微分的步骤反复试凑调试，观察仿真结果，以便得到满意的控制效果，各个控制参数最终调得分别为[0.5 0 1.4],[0.4 0 1.4],[0.3 0 1.0]。图5中，基于PID控制算法的姿态角Φ、θ、ψ的响应曲线超调量分别为14.4%、13.1%和15.7%，上升时间分别为0.9 s、0.94 s和1.3 s。图5中，基于PDF控制算法的姿态角Φ、θ、ψ的响应曲线超调量分别为0.505%、0.505%和0.505%，上升时间分别为0.77 s、0.77 s和0.78 s。可知，在阶跃输入、无干扰的情况下，PID控制器经过多次调参后，仍有较小的超调，而PDF控制器则几乎无超调，且它们的上升时间相差不大。

3.2 抗干扰能力比较

通过模拟在第20 s给机体轴X轴施加一个阶跃负载转矩为1 N·m，得到的仿真结果如图6～8所示。

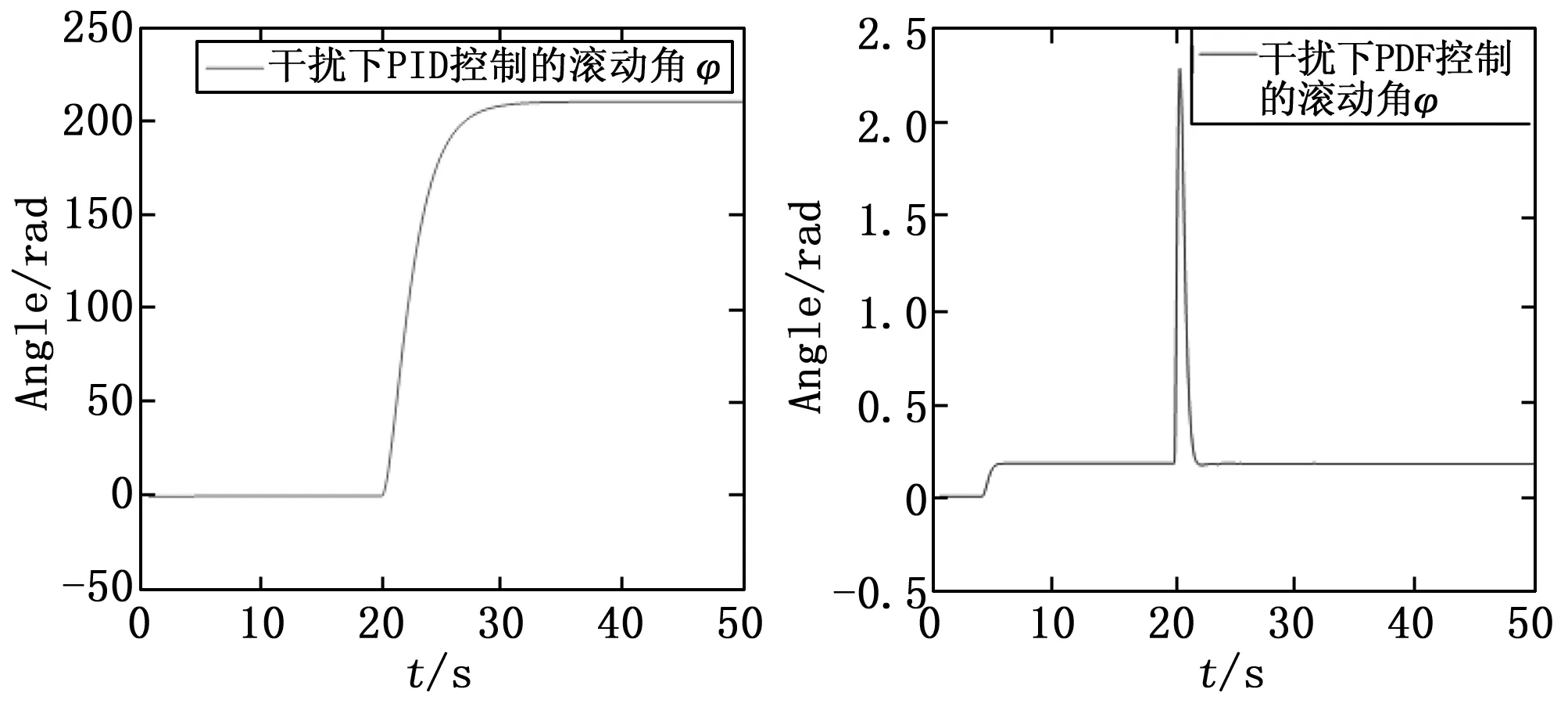
图6 干扰下PID和PDF控制的滚动角

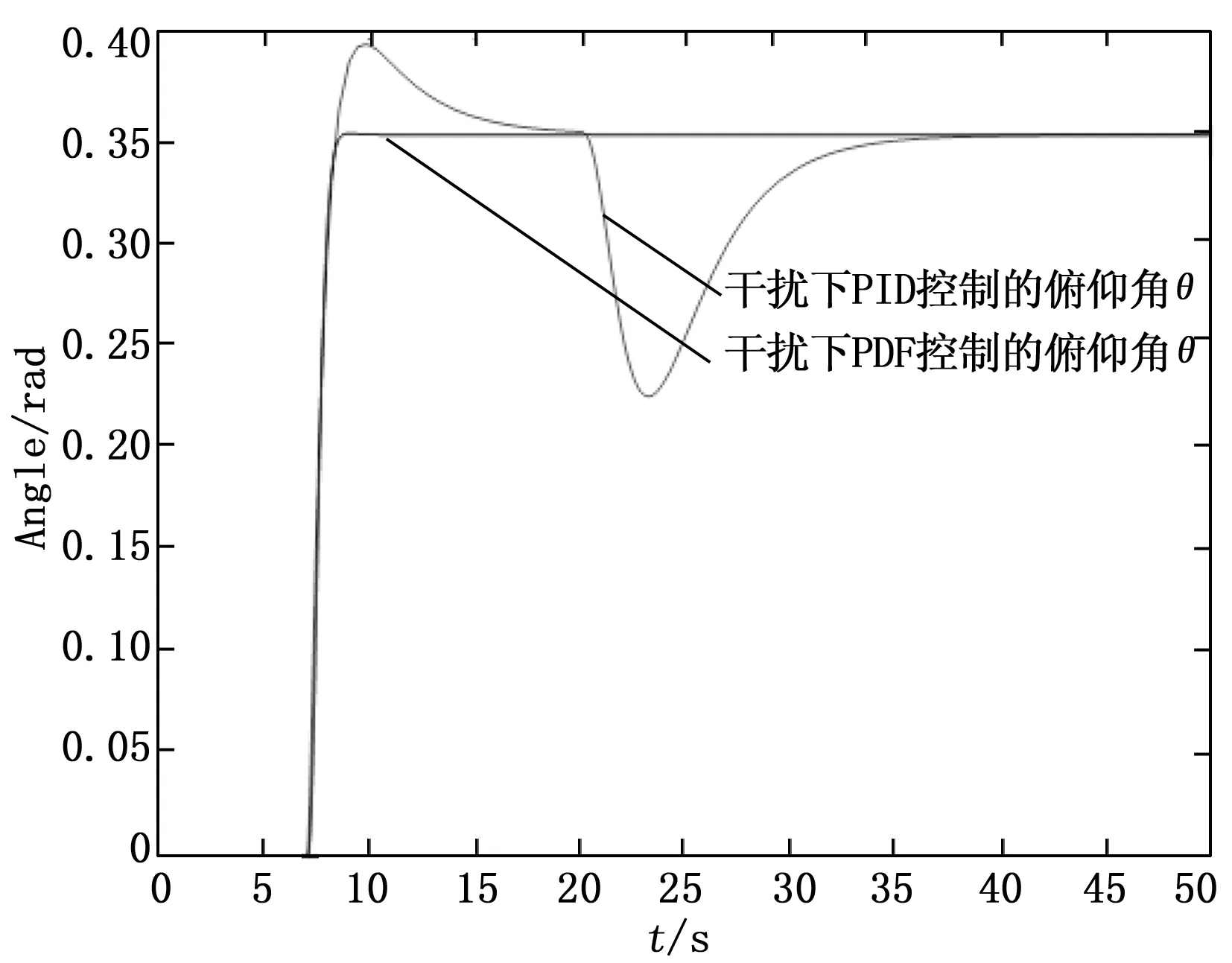
图7 干扰下PID和PDF控制的俯仰角

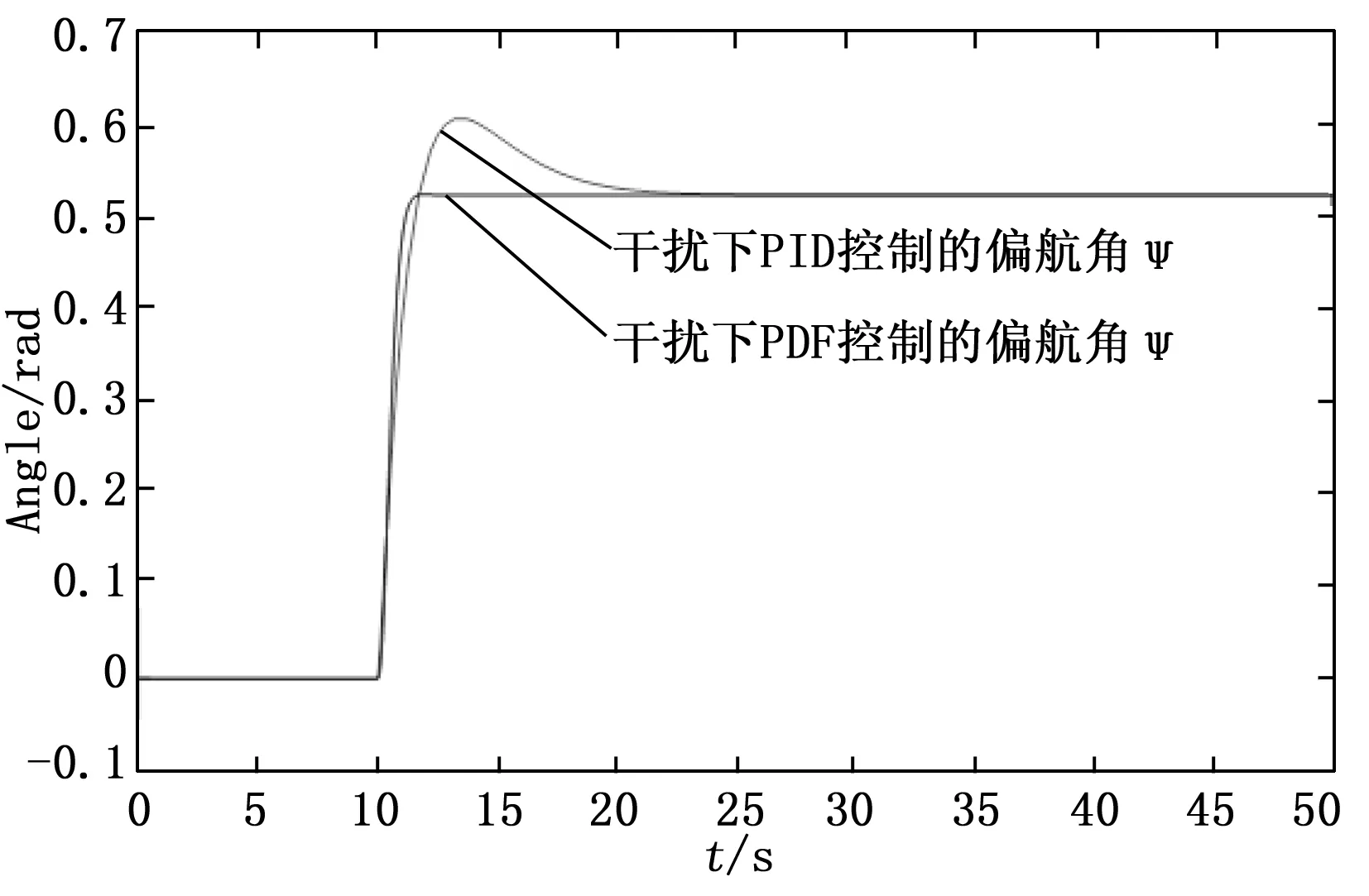
图8 干扰下PID和PDF控制的偏航角

由图6～8可知，在阶跃输入姿态控制器响应稳定后，当给仿真模型系统一个较大的外在干扰力矩时，该干扰使得系统的总力矩相比原来的力矩瞬时增加数倍，基于PID控制器的滚动角姿态响应会立刻出现失稳的情况，并且由于耦合的原因，使得俯仰角的控制会受到干扰，最终使得整个控制系统不可控。但是在PDF控制器下，虽然滚动角也会受到扰动影响，但是立刻就会恢复到设定的姿态角度，并且不会影响到俯仰角的控制，姿态控制完全受控，对四旋翼的整体控制基本上没有影响。

4 结束语

本文以四旋翼无人机为研究对象，在某些假设的条件下，对它的运动学和动力学进行了理论分析，然后建立了四旋翼无人机的简化数学模型，并在Matlab/Simulink软件平台上对四旋翼无人机的高度和姿态控制建立了基于PID和PDF两个控制器的仿真模型和工况仿真。仿真结果表明：采用PDF控制策略的四旋翼姿态控制系统仿真结果符合理论分析，较短的系统响应时间，极其小的超调或无超调，转矩波动小，较好的稳态性能，具有很强的鲁棒性，相比传统的PID控制策略有更好的控制效果。在外部干扰下也能够达到很好的动态响应，并快速恢复到命令姿态角度。对今后PDF控制在四旋翼无人机姿态控制中的研究与应用有一定的实际意义。