一类具有拟牛顿形式的共轭梯度法

李安玭，刘海林

(1.广州工商学院，广东 广州 510850；2.广东技术师范大学，广东 广州 510665)

0 引言

对于无约束优化问题：

其中Rn为n维欧氏空间，f:Rn→R连续可微且有下界，且gk=∇f(xk)，通常用较低存储且计算量更小的共轭梯度法来解决.其基本思想即通过迭代法来产生一点列：

其中αk为步长因子，由某种线搜索确定，通过该线搜索产生的搜索方向dk满足：

这里的βk为算法参数，且gk=∇f(xk).

显然，在非线性共轭梯度法的求解过程中，不同的步长因子αk＞0和参数βk确定了不同的共轭梯度法.本文提出的新算法主要依赖于非精确线搜索方法中常用的Wolfe线搜索：

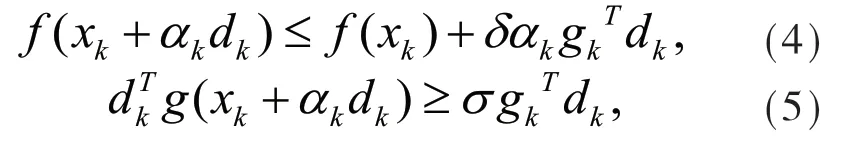
其中0＜δ≤σ＜1.

Perry[1]提出了一类共轭梯度法，它被许多学者认为是最有效且稳健的共轭梯度法之一[2]-[7]，其中的参数βk定义如下：

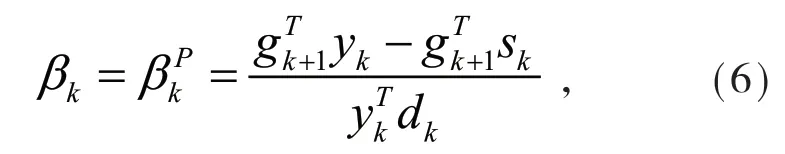
其中yk-1=gk-gk-1，sk=xk+1-xk.Perry提出的这个方法的优点在于，由(3)、(6)式产生的搜索方向具有拟牛顿形式:

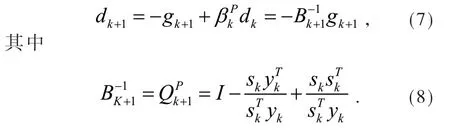
实际上，Andrei作出此修正的目的是将Dai-Liao[9]提出的共轭梯度法（DL方法）中的近似矩阵Qk+1对称化，DL方法中的Qk+1定义为：

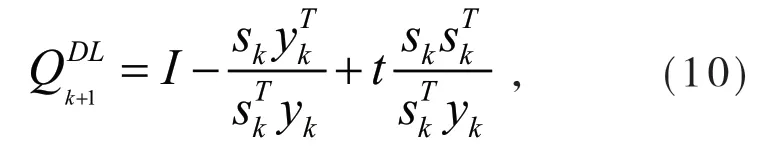
对应的参数βk为：

受上述研究者的启发，本文将提出一个类似Perry方法的共轭梯度法，其中的参数βk为：

本文将在第二部分给出新算法(NP方法)的拟牛顿形式，并对(12)式中的参数t作出讨论及选取，最后给出完整的算法；在第三部分，算法的全局收敛性将建立在Wolfe线搜索的条件下进行论证分析；最终的数值实验结果将在第四部分给出，表明算法的有效性和可行性.

1 参数t的选取与完整算法

考虑到NP方法中的参数βk由(12)式给出，通过结合Perry方法中的推导思路，我们给出以下分析:

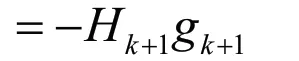
因此，NP方法的拟牛顿形式可如下表示：

实际上，当步长因子αk满足Wolfe线搜索条件中的(5)式时，我们可以得到.接下来，我们将对(15)式中的参数t的选取作出详细讨论.此前，建立在Saman Babaie-Kafaki[11]关于DL方法提出的理论基础上，我们需要对近似矩阵Hk+1的相关性质作出讨论.首先通过下面的这条定理，它表明了矩阵Hk+1的特征根都是实根，这一点对于保证矩阵Hk+1的正定性至关重要.

定理2.1令Hk+1如(15)所定义，则Hk+1是一个非奇异矩阵，且它的特征根为1(n-1重)、λ,其中λ=ak-bk，且

此外，矩阵Hk+1的特征根均为实根.

证明：不妨将矩阵Hk+1写成如下形式：

为了保证近似矩阵Hk+1的正定性，也就是确保矩阵Hk+1的所有特征根都是正实数，即要求它们满足ak-bk＞0.由此易知应满足

因此，只要满足(23)式，NP方法中的近似矩阵Hk1+就是正定的.并且，由(14)式我们可以得到：

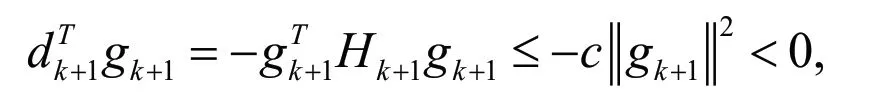
其中常数c=min{λ,1}，也就是说由NP方法产生的搜索方向是充分下降的.

下面我们将通过讨论如何保证算法的稳定性来选取适当的参数t，这一工作需要通过矩阵Hk+1的条件数来完成.对于一个矩阵A，其条件数定义为：

矩阵的条件数的意义在于研究一个矩阵在计算中的敏感性，即受其他数据影响的程度.一般来说，正交矩阵的条件数为1，若一个矩阵的条件数太大（远大于1），我们就说这个矩阵是病态的.下面的性质表明了矩阵的条件数与矩阵特征根之间的关系.

2 全局收敛性

在这一部分，我们需要建立在以下基本假设之上对NP方法的全局收敛性作出分析.

3 数值实验

由于DY方法具有良好的高效性和数值表现，是经典共轭梯度法中较优秀的方法之一，且前面提到的HZ方法也是具有拟牛顿形式的共轭梯度法，我们在这一部分对NP方法、DY方法和HZ方法在强Wolfe线搜索下进行数值实验的对比，比较项为迭代次数、函数值计算次数、梯度值计算次数和CPU时间.(4)(5)式中的参数取值为：δ=0.01，σ=0.1.所选取的测试函数来源于文献[16]，并且算法在或者迭代次数超过9999次时终止，测试所得的实验数据将通过MATLAB进行绘图处理得到直观的比较图像.测试代码通过Visual Studio 2012编写，运行环境为PC 2.7GHZ CPU，4G Memory，Windows 10操作系统，测试函数来源于Dolan and More[17]，他们在文中给出如下定义：P为测试函数集，S为算法集，nS和nP分别表示算法的个数和测试函数的个数，tp.s表示用某个算法s求解某个测试函数P所需的耗费，以及性能比

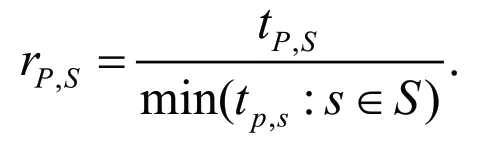
其中，性能比的定义可以理解为不同算法的耗费与其中最小耗费的比值.假设在所有的耗费中最小的耗费量为a,即min(tp,s:s∈S)=a，显然，其他的耗费必定会大于a.并且，若性能比rp,s的值越小，则表明算法s求解测试函数P的耗费越小，数值表现则越好，反之则表明耗费越大，对应的数值表现即越差.另外，文中给出了性能比分布函数：

上式定义的性能比分布函数单调递增且分段连续，结合性能比的定义式可以看到，值越小，算法求解测试函数的耗费就越小，数值表现也就越好.由(34)式可以发现，实验图中靠左的曲线反映的是算法中表现为优的数值与所有数值的比，靠右的曲线则反映算法能够成功求解的测试函数与所有测试函数的比值.考虑整体的图像，可以理解为，越靠上的曲线就具有越强的处理测试函数的能力，其对应的算法相较对比项越优，且越有效.

以下是通过MATLAB得到的三种方法的测试结果对比图像：

图1 算法迭代次数的对比图

图2 函数值计算次数的对比图

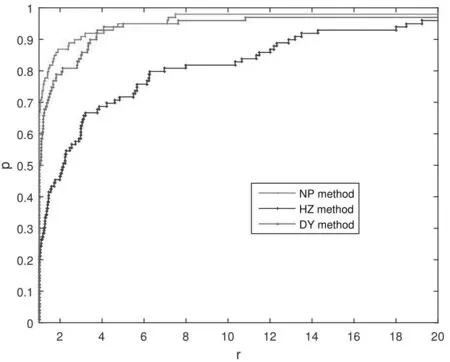
图3 梯度值计算次数的对比图

图4 耗费的CPU时间对比图

由上面的数值结果对比图像可以看到，NP方法的数值表现要比HZ方法和DY方法更好一些，证明本文提出的NP方法不仅具有足够的稳定性，而且在应用于求解大规模无约束优化问题时是有效的.