陶瓷刀具切削航空难加工材料的表面形貌试验研究

李景贺， 陶广福， 赵灿， 奚望

（1.黑龙江科技大学 机械工程学院，哈尔滨150020；2.桂林航天工业学院 能源与建筑环境学院，广西 桂林541004；3.江苏威尔五金股份有限公司，江苏 盐城224200）

0 引 言

随着第四次工业革命的到来，我国正快速步入智能化、信息化、高度自动化的先进制造时代，需要高精技术支撑的航空航天领域内的制造业对于基础制造技术的要求也愈发严格。陶瓷刀具以其优异的高硬度、耐热性、耐磨性和化学稳定性，在高速切削难加工材料方面显示了极大的优势[1]。陶瓷刀具是众多先进刀具的一种，因此在陶瓷刀具的应用过程中，合理地选择加工工艺参数具有重要的工程意义。针对陶瓷刀具在加工过程中的技术应用数据、材料属性、磨损机理等关键性能参数，众多学者对陶瓷刀具的使用展开了卓有成效的研究[2-5]。在航空航天领域关键零部件成型技术的应用过程中，镍基高温合金GH4169以其具备的优异耐高温性能而被广泛应用于航空航天领域关键零部件的热端部位中，如火箭发动机和航空喷气发动机热端部件等核心零件。针对镍基高温合金GH4169的加工性能及其在航空航天领域关键零部件的材料性能，赵玉涛等[6]采用光学显微镜和扫描电镜观察了一涡轮叶片的微观组织，探讨了不同影响因素对组织的影响。蔡明等[7]采用单因素试验法探究了镍基高温合金的磨削表面工艺性能。靳盛哲等[8]为探究孔挤压工艺在镍基高温合金的应用，通过建立孔挤压工艺的数值模拟方法，并通过试验验证方法的有效性，讨论了芯棒材料、挤压量和摩擦因数对周向残余应力分布的影响规律。张文涛等[9]针对镍基高温合金GH4169加工效率低和切削刃磨损严重的问题，采用单因素试验法仿真探讨了切削用量对切削力和切削温度的影响规律。高东强等[10]通过建立有限元模型并分析切屑形态、切削力，以及切屑锯齿化程度和切削力曲线图，优化选取了合适的切削速度与切削深度。本文通过以工程现场常用的切削工艺参数为正交试验的分析数据，以加工镍基高温合金GH4169后的表面形貌为研究对象，优化选取了最佳工艺参数，并在建立表面形貌的数学模型基础上进行了实验验证，具有重要的工程指导意义。

1 表面形貌的研究

对于航空航天领域的关键零件而言，其制造精度要求较高，表面质量除包括工件表面粗糙度之外，还有工件的表面形貌等。本文所研究的镍基高温合金GH4169因被广泛应用于航空航天、军工装备、船舶制造业等尖端领域，故对零件的加工精度要求较高，因此针对镍基高温合金GH4169铣削加工得到的表面形貌进行试验研究具有重要的工程意义。

零件的表面形貌是指在加工过程中，刀具相对于工件表面运动，并在完成加工任务后，在工件表面留下刀具路径的轨迹，是用来表征工件质量的指标。针对普通机床而言，工件表面形貌的优劣主要取决于切削用量的选取和刀具几何参数的设定。而对于高速铣削加工而言，工件的表面形貌除取决于铣削参数的选取和刀具几何参数的设定之外，还与刀具的振动、磨损、机床的刚度等因素有关。

2 表面形貌纹理理论分析

对于铣削加工，工件表面存在纵向残留高度和横向残留高度，所谓纵向残留高度是指铣刀沿Y轴（笛卡尔坐标系确定法则确定）进给方向移动，在加工表面留下的凸起与铣削宽度的移动方向一致；而横向残留高度是指铣刀沿进给方向移动，在加工表面留下的铣刀纹路。铣削表面纹理如图1所示。

由图1(a)可知，在铣削加工中，纵向残留高度连续出现，并与刀具轨道路径一致，表面纹理较为明显；图1（b）中，横向残留高度的产生是断续的一段弧线，其间隔与进给速度有关，形成方向与进给方向一致，由于在铣削过程中，进给量远小于铣削宽度，故横向表面纹理较纵向纹理不甚明显，因此在对横向纹理进行观测研究时，需借助放大设备。加工后的工件在纵向纹理和进给纹理的共同作用下，最终形成各种各样的表面形貌，如图2所示。图2中:Hc表示横向残留高度之间的间距;Hz表示纵向残留高度之间的间距;h表示铣削结束后工件表面的残留高度。

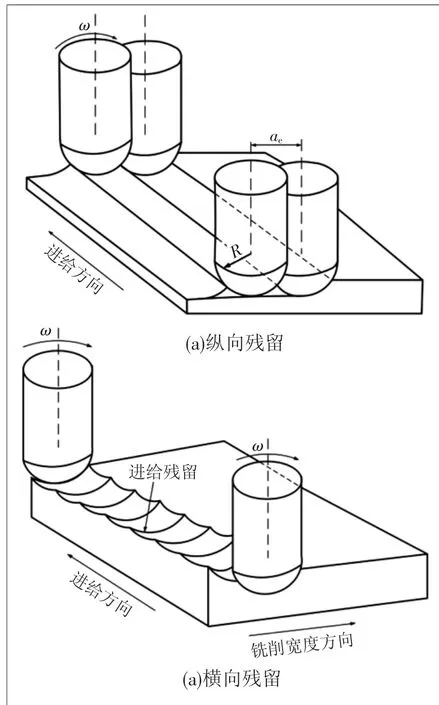
图1 铣削表面纹理

图2 表面形貌示意图

3 表面形貌铣削试验

3.1 试验材料

本文所采用的航空难加工材料GH4169为典型的镍基高温合金材料，是目前生产量最大的高温合金。GH4169的镍含量高达50%～55%，其余主要元素有Fe、Cr、Nb等，其化学成分如表1所示。

表1 GH4169化学成分质量分数 %

GH4169是以体心立方Ni3Nb（γ"）和面心立方Ni3(Al、Ti、Nb)（γ′）强化的镍基高温合金。其中γ"相数量最多，是合金的主要强化相。在中温700 ℃以下具有高的屈服强度、拉伸强度和持久强度，同时具有良好的成形性和焊接性，其物理力学性能如表2所示。

表2 GH4169物理力学性能

3.2 实验条件

实验用陶瓷刀具铣削机床为汉川XH714D立式加工中心，主轴转速范围为60～8000 r/min，X/Y轴快速移动速度为20 000 mm/min，Z轴快速移动速度为15 000 mm/min，X/Y/Z轴进给速度为：5～5000 mm/min。试验观测设备采用VHX-1000超景深三维显微镜，如图3所示。

图3 VHX-1000超景深三维显微镜

3.3 正交实验参数设定

正交实验的参数设定如表3所示。

表3 铣削参数

3.4 试验结果分析

通过正交实验借助VHX-1000超景深三维显微镜观测已加工工件的表面横向残留高度纹理，并测量各组参数下，横向纹理之间波峰和波峰之间的间距，记录于表面形貌正交实验结果表中，如表4所示。

对于表面形貌，纵向残留高度间距和横向残留高度间距越小，表面纹理越密集，工件装配时越牢靠，抗磨损能力越强。该实验中铣削宽度ae=10 mm保持不变，故纵向残留高度的间距一致，则已加工工件的表面纹理主要与横向残留高度的间距有关。表4中只记录横向残留高度间距的值，故在该实验条件下，横向残留高度间距Hc越小，被测加工工件的表面纹理越密集。

表4 表面形貌正交实验结果

为观测影响横向残留高度间距各因素间的主次关系，文章利用极差分析法，直观找出各铣削参数对表面形貌影响的主次，表面形貌极差分析如表5所示。

表5中:k1为各因素第一水平横向残留高度间距平均值；k2表示各因素第二水平横向残留高度间距平均值；k3表示各因素第三水平横向残留高度间距平均值；k4表示各因素第四水平横向残留高度间距平均值；R为横向残留高度间距极差值。

由表5可知，各工艺参数的极差大小关系为Rfz>Rap>Rv，故对表面形貌的影响大小顺序为：每齿进给量fz、铣削深度ap、铣削速度v。为获取较好的表面形貌，各因素水平平均横向残留高度间距应尽可能小，故每齿进给量fz取第一水平，铣削深度ap取第一水平，铣削速度v取第二水平。故获得较好表面形貌的最佳参数组合是v2ap1fz1，同表5 中的结果相比，发现v1ap1fz1参数组合与理论上最佳参数组合最为接近。工艺参数下的实际表面纹理如图4 所示（以第一组为例）。

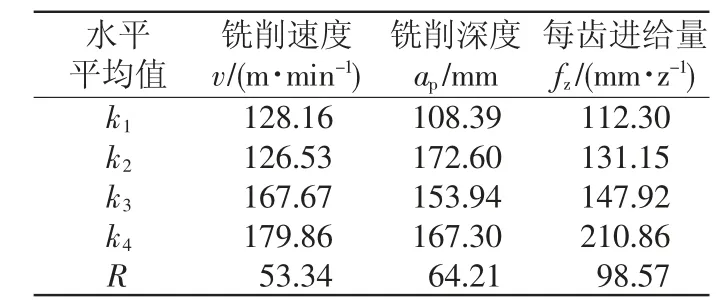
表5 表面形貌极差分析

图4 放大300倍率下第一组表面纹理图

4 表面形貌横向纹理的形成建模

针对试验中，表面形貌形成机理建立幂指数的数学回归模型，如下式：

式中：Hc为横向残留高度间距；Kc为除主要铣削参数外，与材料性质、铣削条件相关的修正系数；h1、h2、h3为铣削参数的各个影响因子系数。

式（1）等式左右两边同时取对数，可以得到如下线性关系式：令lg Hc=Y，lg Kc=A，lg v=x1，lg ap=x2，lg fz=x3，式（2）可简化为

由表4可知，各参数组合对应的横向残留高度间距值均已测出，但并非所有参数均可靠。试验中，因存在变换刀具刀面、刀具刃口磨损、工件表面被飞屑刮伤等现象，致使测量结果偏高。因此，为获取准确可靠的表面形貌横向纹理经验公式，需要剔除一些参数组合，参数拟合数据点的表面形貌误差分析如表6所示。

表6 表面形貌误差分析

对表6中各参数求解，可得各组参数对应的Y、x1、x2、x3值。将此数值进行多元线性回归拟合，得到式（3）中未知参数A、h1、h2、h3值。即A=0.1932，h1=1.2488，h2=-0.7421，h3=1.1073，对A求反对数得Kc=1.5603。将此数值代入式（1）中，得：

通过将每组实验参数代入式（4），对得到的经验公式进行误差分析。可得到每组参数下横向残留高度间距Hc的理论值，并根据相对误差的计算法则，求得每组参数下横向残留高度间距的相对误差。以表5中第一组参数为例，其相对误差计算方法如下：

式中：ε为相对误差；Hce为横向残留高度间距实验值；Hct为横向残留高度间距理论值。

同理，可得每组参数对应的横向残留高度间距的相对误差，其值分别为9%、2%、2%、13%、1%、21%、18%、10%、3%、8%、7%、5%，其平均相对误差值为8%。

由于在实际加工过程中，影响表面形貌的因素较多，如机床振动、实验温度、铣削过程中过热切屑的不规则运动、铣削参数间的相互作用等，故就结果而言，表面形貌横向纹理模型计算所得理论值与实验值基本一致。证明文中表面相貌横向纹理模型是可靠的。

5 结 论

1）本文以陶瓷刀具铣削航空难加工材料镍基高温合金GH4169时获取的加工表面形貌为研究对象，以工程现场常用铣削参数为正交实验分析数据，对比分析了各组工艺参数下的工件表面形貌，优选出获取最佳表面形貌时的切削工艺参数。即在第一组参数组合下，所测得的表面形貌横向纹理间距值较小，故应选用的铣削参数为铣削速度v为300 m/min，铣削深度ap为1.5 mm，每齿进给量fz为0.05 mm/z，此时所得的表面形貌横向纹理间距Hc为47.72 μm。

2）基于正交实验所得的数据，进行表面形貌横向纹理数学模型的建立。由于铣削过程中，表面形貌横向纹理的影响因素较为复杂，故建立复指数模型来描述表面形貌横向纹理。通过对实验数据进行多元线性回归拟合，得到相关影响系数，从而建立了表面形貌横向纹理数学模型。通过误差分析，计算各组数据对应的相对误差，进而求得表面形貌横向纹理间距的平均相对误差，各表面形貌横向纹理间距的实验值与理论推导值的平均相对误差为8%，证实了表面形貌横向纹理模型的可靠性。