我国城市新冠肺炎发病率的地理分布格局：人口迁徙与社会经济因素的影响

梁 泽， 王玥瑶， 孙福月， 梁琛瑜， 李双成*

1.北京大学城市与环境学院， 北京 100871

2.北京大学地表过程分析与模拟教育部重点实验室， 北京 100871

2019年底暴发的新型冠状病毒肺炎(COVID-19，简称“新冠肺炎”)疫情是自2003年非典型肺炎疫情以来的又一次重大世界突发公共卫生事件[1-4]. 面对疫情蔓延，武汉以及其他疫情重灾城市紧急应对. 新型冠状病毒的高传染性、高重症率使及时追踪、诊断并隔离感染人员成为控制疫情蔓延的关键. 我国各城市公共卫生系统同时面对病毒感染检测、感染者收治、医务资源调度、贯彻管控政策阻断病毒传播链等多重挑战. 因此，城市的经济发展水平、医疗卫生资源水平以及公共管理能力等多维度的差异使不同城市的新冠肺炎发病率呈现显著的差异，部分城市新冠肺炎发病率在疫情初期剧烈上升[4]. 我国在近几十年经历了高速的城市化进程，城镇基本医疗保障逐步到位，传染病大规模传播事件大幅减少，传统传染病如天花、霍乱、黄热病等基本消失[5]，公共卫生应急能力有一定的提升. 然而，新冠肺炎疫情在我国各城市的快速传播表明，当前城市系统在面对新型传染病(如SARS、登革热和新冠肺炎)等突发疫情的冲击下，仍与理想的“健康城市”目标存在差距.

根据流行病学原理，传染性疾病的传播可分为生态学过程(ecologic process)和社会过程(social process)[6]. 城市间交通体系的完善有利于疫情在城市间扩散，同时，空间上的邻近效应使疾病能在城市内部不断传播. 城市的社会经济发展与上述两种传播过程有着密切关联，尤其影响以社会过程为主体的传染病传播方式，并最终影响城市中人群的总体发病率. 随着大规模的城市化进程在全球展开，为了改善城市的灾害应急协调能力，有效阻断传染病的传播，给城市居民提供可靠、持久的健康保障[7]，国际上医学、公共卫生、城市规划等多领域学者共同提倡追求系统而严格的“健康城市”标准[8-11]. 该标准包括为市民提供安全的环境，如提升城市的医疗服务能力、公共财政投入、社会生产水平以及增加绿地空间配置等[12-14].

然而，目前关于城市的经济发展水平、医疗服务能力、公共财政投入、绿色空间配置等指标如何，以及在多大程度上影响突发传染病疫情冲击下城市对居民健康的保障能力，仍然缺乏足够的实证. 评估我国城市的社会经济特征与新冠肺炎发病率的关系具有重要的科学与实践意义. 此外，传染病的发生、流行、分布等除了与病毒自身生物学特性[15]、“健康城市”特征有关之外，还与空间信息相关，如与早期疫情重灾区的空间距离、本地以及邻近区域的气候与气象条件以及自然地理环境等[16-20]. 这些空间属性往往打破了经典流行病学中的样本相互独立的基本假设，使自变量与因变量出现空间依赖性或空间自相关，呈现各因素的影响力随着空间位置而发生变化的空间非平稳特征. 在新冠肺炎疫情研究中忽视数据的空间自相关性和影响的空间非平稳性，会造成变量间关系挖掘不够等问题，使统计结果出现偏倚[21-23].

地理加权回归模型(Geographically Weighted Regression，GWR)由Fotheringham等于1996年提出，是有效处理回归分析中的空间自相关与空间非平稳性现象的建模技术[24]. 该模型通过引入数据的空间位置，利用非参数估计方法在每个地理位置给出函数的局部估计量，可以有效弥补普通最小二乘法只能在全局或者平均意义上对参数进行估计、无法反映空间局部变化等不足，被成功应用于一系列流行病学研究. 例如，董冲亚等[25]基于GWR模型发现，城乡类型对我国女性肺癌发病的影响强度存在东西地区差异，纬度指向因子影响强度存在南北地区差异；肖雄等[26]发现，GWR模型较普通最小二乘回归模型(OLS)能更加深刻地揭示血吸虫病血检阳性率与社会经济学因素、自然环境的复杂关系及其空间依赖. 在应用地理加权回归模型过程中，首先使用空间自相关分析检验模型适用性也是重要的研究内容之一[27-28]. 结合空间自相关分析及地理加权回归模型探究新冠肺炎疫情的空间分布特征，对深入认识新冠肺炎疫情的影响因素及其空间差异具有重要意义[29-30].

武汉市自古号称“九省通衢”，是我国的重要交通枢纽. 武汉作为早期新冠肺炎疫情灾区之一，其特殊的地理位置加上春运期间的大量跨区域流动，给病毒的远距离传播提供了极佳机会，造成了新冠肺炎疫情在部分地区的快速流行. 部分人口流动频繁的城市成为新冠肺炎疫情的高风险区[31]. 因此，在研究城市社会经济指标对疫情影响的过程中，有必要加入基于异地人口迁徙情况的控制变量.

基于以上背景，该文以我国282个城市单元(包括4个直辖市，15个副省级市以及263个地级市)为研究区，基于2020年1月1日—3月5日疫情持续期间的城市逐日新冠肺炎累计确诊病例数据、百度地图迁徙大数据和《2018年中国城市统计年鉴》数据，使用普通最小二乘法线性回归模型、空间自相关和地理加权回归模型，研究全国迁入率、武汉迁入率、人均医务人员数量、人均绿地面积、人均国内生产总值以及人均公共财政投入共6项指标对城市尺度新冠肺炎发病率的影响及其空间依赖特征. 我国城市化已进入中后期阶段，亟需从城市安全的视角来检视人口迁徙与多维度社会经济特征对新冠肺炎疫情的反应与响应，通过高质量城市化规避风险，增进韧性，提升城市公共卫生安全水平. 该文分析结果可为深入理解城市重要社会经济指标对新发重大传染病疫情灾害响应能力的空间异质性及其驱动机制提供参考.

1 数据与方法

1.1 研究区概况

该研究以我国282个城市(包括4个直辖市，15个副省级市以及263个地级市)为研究单元. 该研究范围通过以下方法确定：首先，基于《2018年统计年鉴》数据获取全国所有直辖市、副省级城市以及地级市的统计指标；然后，将这些统计指标与各城市新增新冠肺炎确诊上报数据以及城市尺度的百度人口迁徙数据进行匹配，去除空值数据，共得到283个城市单元；最后，鉴于大量城市在疫情初期的确诊病例多为武汉输入性病例，为了横向评估各城市受到武汉输入人口的影响，笔者未将武汉市的数据加入分析，最终得到282个城市单元用于研究.

1.2 数据来源

城市尺度的新冠肺炎新增确诊数据来自2020年1月1日—3月5日国家卫生健康委员会和丁香医生的网络公开数据. 该研究通过对以上两个数据源数据的对比和整合，解决了丁香医生部分早期数据不准确的问题. 同时段的城市尺度人口迁徙数据来自百度地图迁徙大数据平台，该数据通过对比百度用户地理位置的变化，将8 h内所有位置发生变化的智能终端用户数量进行计算分析，全覆盖铁路、公路、航空等各类交通工具. 获取数据包含迁入地、迁出地、流动时间、热度值、迁徙规模等属性，弥补了传统人口调查方法难以迅速统计海量人口的异地迁徙情况的不足. 其中，迁徙规模字段表示当天迁入或迁出该城市的总量，热度占比为其他城市迁入该城市数量占迁徙规模的比例，热度值为迁徙规模与热度占比的乘积. 统计年鉴数据来自《2018年中国城市统计年鉴》，主要包括所有研究单元的4项重要社会经济统计指标，即地方一般公共预算支出、地区生产总值、绿地面积和执业(助理)医师数.

1.3 研究方法

1.3.1新冠肺炎发病率计算方法

基于2020年1月1日—3月5日各研究单元的新冠肺炎累计确诊病例数据(cumulative confirmed cases，CCC)以及从统计年鉴获取的2018年城市年均人口规模(population size，PS)，计算得到城市人群的新冠肺炎发病率(incidence rate，IR)指标〔见式(1)〕：

IR=CCCPS

(1)

1.3.2全国迁入率、武汉迁入率与人均社会经济指标计算方法

基于研究单元2020年1月1日—3月5日来自全国所有城市的平均迁入热度值(migration intensity from all other cities across the country，MIall)与迁入目标城市的2018年年均人口规模(population size，PS)，计算得到每个研究单元的全国迁入率(migration rate from all other cities across the country，MRall)，即来自全国其他城市的人口迁入率〔见式(2)〕：

MRall=MIallPS

(2)

同时，基于研究单元2020年1月1日—3月5日来自武汉的迁入热度值(migration intensity from Wuhan，MIw)，计算得到每个研究单元的武汉迁入率(migration rate from Wuhan，MRw)，即来自武汉的人口迁入率〔见式(3)〕：

MRw=MIwPS

(3)

以获取的各研究单元的公共预算支出、地区生产总值、绿地面积和执业(助理)医师数4个指标为分子，以PS为分母，计算得到人均公共预算支出、人均地区生产总值、人均绿地面积和人均医务人员数量4个人均社会经济指标，这4类指标分别从宏观上测度城市的公共投入与服务水平、地区社会经济发展水平、绿色空间配置情况以及医疗服务能力.

1.3.3普通最小二乘回归与地理加权回归模型

以全国迁入率、武汉迁入率、人均公共预算支出、人均地区生产总值、人均绿地面积和人均医务人员数量6个指标为自变量，以新冠肺炎发病率为因变量，分别建立普通最小二乘法线性回归模型和地理加权回归模型.

最小二乘法是常用的线性回归模型，计算公式：

(4)

式中：yi为第i个研究单元的因变量观测值；xij为第i研究单元(i=1,2,…,m)中第j个自变量值(j=1,2,…,n)；β0为回归常数；εi表示第i个研究单元的独立分布随机误差项；m为研究单元样本数量(m=283)；n为自变量个数(n=6). 然而，OLS模型仅适用于对参数进行平均或全局意义上的估计，难以保证参数的平稳性.

作为一种改进的回归模型，GWR模型通过区域地理位置函数作为模型参数，进一步在空间范围内每个位置估计局部回归方程，从而实现对研究对象在某一尺度下的空间变化及相关驱动因素的评估目标[32-33]. 由于GWR模型充分考虑了空间对象的局部效应，通常具有更高的准确性，计算公式：

(5)

式中，(ui,vi)为研究单元i的经纬度坐标，βj(ui,vi)为研究单元i的第j个回归参数，xij为第i个研究单元的第j个变量. 在估算研究单元i的回归参数时，利用邻近区域观测值的子样本信息进行局部回归. 研究单元i的回归参数可通过使式(6)达到最小来估计：

(6)

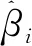
(7)

1.3.4空间权函数

wij=e-βdij2

(8)

式中：β为带宽参数，表示权重随距离增加衰减的越慢的程度；dij表示研究单元i与j之间的地理距离. 式(8)中带宽参数(β)的确定会对估计结果有重要影响，带宽过大会使回归参数估计的偏差过大，带宽过小会使回归参数估计的方差过大. 为了使局部回归系数估计结果更准确，该研究采用赤池信息(AIC)准则来确定最优带宽β.

2 结果与讨论

2.1 新冠肺炎发病率的空间分布特征

我国新冠肺炎发病率分布的空间特征如图1所示. 结果显示，武汉周边城市的新冠肺炎发病率显著高于其他地区，而东北部分地区和东南沿海部分地区同样存在部分高值区，高值区具有较为明显的空间聚集特征. 东部沿海地区城市新冠肺炎发病率普遍高于南部沿海地区城市，西北和西南地区的新冠肺炎发病率相对较低.

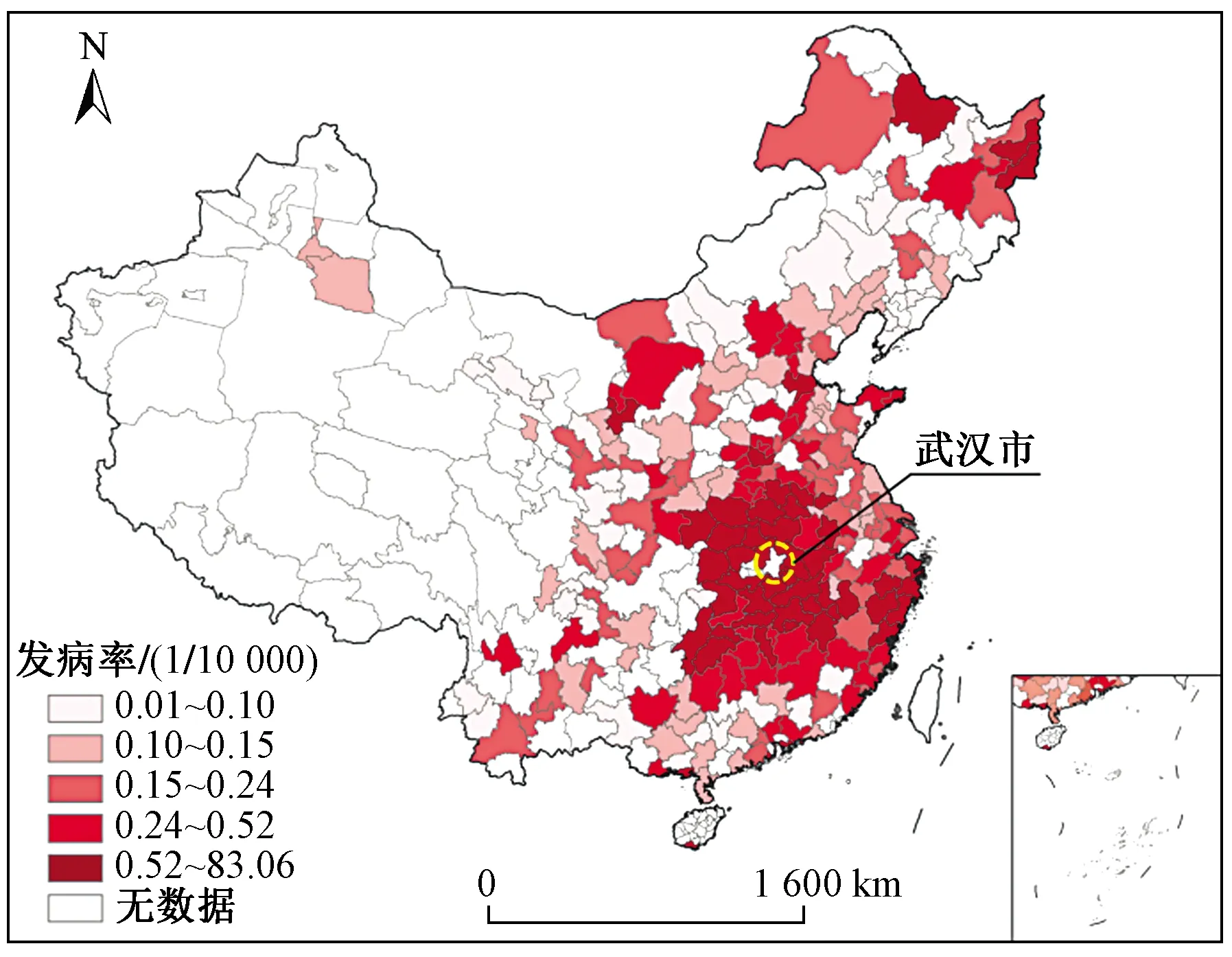
注： 底图源自国家测绘地理信息局(http:bzdt.nasg.gov.cn). 审图号：GS(2019)1697号. 下载日期：2020年1月20日. 下同.

2.2 OLS模型结果

该研究首先选用传统的OLS模型建立6项人口迁徙及社会经济指标与新冠肺炎发病率之间的关系，为进一步确定是否选择GWR模型提供对照参考. OLS模型估计结果见表1，结果显示，模型整体拟合度较低，整体R2仅为0.015. 参与回归的6个变量中，除了人均地区生产总值指标外，大多数变量对新冠肺炎发病率的整体回归系数不显著. 对OLS模型回归结果得到的残差进行空间可视化，结果显示残差具有明显的空间聚集特征(见图2). 进一步对残差做热点分析，结果显示，Jarque-Bera统计量为 169 942.794(P<0.001)，具有统计学意义，表明残差并不服从正态分布的假设. 计算残差的全局Moran′s I指数为0.192，Z-score为15.556(P<0.001)，说明残差项存在显著的空间自相关性.

表1 OLS模型估计结果

图2 OLS模型回归残差空间分布与空间聚类及异常值分析结果

对OLS模型回归结果得到的残差做进一步的空间自相关分析，评估其空间信息是否被充分提取. 空间自相关分析通过局域Moran′s I指数算法，基于ArcGIS 10.6软件中聚类异常值(clusteringoutlier Type)工具计算得到聚类结果(见图2). 结果显示，湖北省除武汉市以外的其他地区以及与湖北省邻近的河南省、江西省、湖南省的部分地区的回归残差均出现明显的高-高聚类特征. 距离武汉市较远的内蒙古自治区连接着东北部分地区、云南省与甘肃省部分地区形成了低值聚类. 高-高聚类区周边则存在一定的高低混杂的异常值地区. 综上，OLS模型对研究单元的空间信息提取还不完全，构建GWR模型对6个自变量的局部回归系数进行更准确估计具有必要性.

2.3 基于GWR模型分析的各因素影响的空间差异

基于GWR模型得到局域分析结果，局部R2和局部回归系数估计值分别如图3、4所示. 从基于全样本的模型评估结果来看，GWR模型显著提升了整体拟合度，其回归整体R2达到0.40，远优于OLS模型的拟合效果(见表2). AIC下降，说明GWR模型结构更合理且对因变量解释的程度更高. 图3揭示了局部R2的空间变异情况，结果显示，GWR模型的局部R2大部分在0.02～0.41之间，但不同区域间的局部R2差异明显. 其中，东北和武汉周边地区的局部R2较大，说明人口迁徙和城市社会经济因素较好地解释了城市之间新冠肺炎发病率的变异；而对于距离武汉较远的西北和西南地区，人口迁徙和社会经济因素对新冠肺炎发病率的解释能力则相对较低.

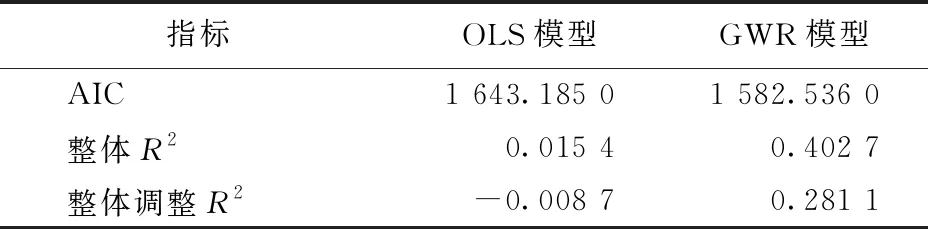
表2 OLS和GWR模型评估结果

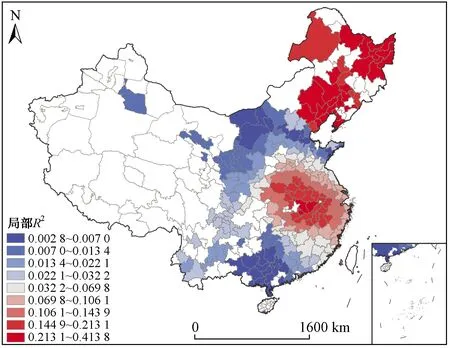
图3 GWR模型局部R2的空间分布

GWR模型回归的局部回归系数评估结果如图4所示. 结果显示，6个自变量的局部回归系数大小变化均具有显著的空间依赖特征. 其中，全国迁入率指标的局部回归系数同时存在正向与负向，说明来自全国各地的异地人员流动并不一定导致城市新冠肺炎发病率的升高. 而作为对照，武汉迁入率指标在武汉周边地区表现出较大的正局部回归系数，表明武汉周边城市的新冠肺炎发病率受到武汉人口输入的强烈影响. 武汉迁入率指标的局部回归系数随着与武汉距离的增加呈现递减特征，表明武汉人口输入的影响存在空间衰减效应. 然而，这种衰减趋势并没有继续延伸至全部地区，如距离武汉较远的东北地区和部分西南地区的新冠肺炎发病率反而受到武汉迁入率的影响较大，其影响程度甚至与武汉周边地区相似. 这种反常现象可能与这些地区政府防控政策落实力度以及居民的防护意识有一定关联.

图4 GWR模型的局部回归系数估计结果

在城市社会经济影响方面，城市人均地区生产总值指标的局部回归系数在经济发展水平相对较高的东南地区呈现绝对值较大的负数，表明该地区的社会经济发展水平对新冠肺炎发病率的控制起到了重要作用. 这些地区人均地区生产总值指标具有较大的正局部回归系数，还可能与当地基础经济水平较高、居民防护意识较强、城市管理与服务人才资源充足、应急管理基础较强等有密切关联. 人均绿地面积指标的局部回归系数仅在全国一定比例的地区为负，而在武汉周边部分地区甚至为正，表明城市总体绿化程度对新冠肺炎等传染病疫情的作用较为复杂. 一方面，研究显示，绿地面积对控制传染病的蔓延具有多重效应，既能通过控制病毒在空气中传播，抑制传染过程，也可能通过影响居民休闲聚集性活动而加快疫情蔓延[34-36]；另一方面，相比人均绿地面积指标反映的城市整体绿化水平而言，绿地的空间格局等则可能起到更重要的作用，难以通过该研究反映出来. 人均医务人员数量指标在大部分地区表现出负的局部回归系数，但在武汉近距离的周边地区并没有表现出对新冠肺炎发病率的抑制作用，这可能与这些地区的统计结果受到省外医务援助力量的投入有关. 此外，笔者还发现，对于武汉周边的城市而言，高人均公共财政支出对城市新冠肺炎发病率的升高起到了重要的抑制作用，这种作用随着与武汉距离的增加呈现规律明显的空间衰减特征. 这表明在应对重大突发公共卫生灾害过程中，城市的公共财政支出能力可能与城市服务能力与管理力度等紧密联系，这对于突发的新冠肺炎疫情蔓延的控制具有至关重要的作用. 这种作用的有效程度可能随着疫情的严重性与突发性相应升高.

3 结论

b) 全国迁入率与武汉迁入率对城市新冠肺炎发病率的影响具有不同的空间变化模式. 总体而言，武汉迁入率对全国城市新冠肺炎发病率的升高具有重要推动作用，这种作用随着与武汉地理距离的增加呈空间衰减特征，但不包括东北和西南部分地区. 全国迁入率指标对新冠肺炎发病率的影响方向与程度呈现特征明显的空间格局，但又不同于武汉迁入率指标影响的空间格局. 这表明人口流动对传染病疫情的影响可能受到自然与人文地理环境等空间属性的影响，但其作用机制有别于早期疫情重灾区人口输入的影响.

c) 高人均地区生产总值对新冠肺炎发病率的控制作用在我国东南沿海等发达地区较为显著，这可能与发达地区城市社会经济水平较高、居民防护意识较强、城市应急管理与服务能力较高等有密切关联. 人均绿地面积对新冠肺炎疫情作用较为复杂，其对疫情的控制作用仅在全国一定比例的地区显著，其中不包括武汉周边地区. 人均医务人员数量指标在全国大部分地区表现出对新冠肺炎疫情蔓延的控制作用，但同样不包括武汉周边地区. 人均公共财政支出对于武汉周边地区新冠肺炎发病率的控制起到了重要作用，该作用随着与武汉距离的增加呈现规律明显的空间衰减特征，表明城市的公共财政支出能力所对应的城市公共资源与应急管理能力的重要程度随着重大突发公共卫生灾害冲击强度的升高而加强.