基于有限元分析的管道焊接修复方法研究

2020-08-01武旭，帅健，狄彦，许葵，单克，3

石油矿场机械 2020年4期

武旭，帅健，狄彦，许葵，单克，3

(1.中国石油大学(北京)安全与海洋工程学院，北京 102249；2.中国石油化工股份有限公司科技部，北京 100728； 3.深圳市燃气集团股份有限公司，广东深圳 518049)①

焊接是管道穿孔局部破坏的常用修复方式[1-3]。现场焊接修复通常采用接管、补板、套管3种修复方法[4-7]。我国对于穿孔管道的焊接修复方法尚无统一的标准规范，对不同焊接修复结构的承载效果尚无统一结论。因此，研究管道常用焊接修复方法的承载能力具有一定的现实意义。

目前，部分学者在该领域进行了一定研究。卜文平、帅健等通过有限元分析和水压爆破试验对接管修复管道承载能力进行了评估[8-12]。Fazzini和Otegui对补板修复的X52钢级输气管道进行了试验研究，发现内压低、缺陷大、补板长、焊接质量差均会引起较高风险[13]。Smith等利用弹性力学理论分析了套管及周边的应力分布，得出增加套管壁厚可以减小焊缝区域的应力水平，环向应力随焊缝尺寸的减小而增大，而轴向应力不随焊缝尺寸改变[14]。Gordon等利用有限元方法对套管修复管道的适用性进行评价，分析了管道壁厚、套管长度和厚度对管道运行安全的影响，并给出了建议值[15]。Woo[16]等采用虚拟裂缝闭合技术，研究了含环向裂纹修复结构在拉伸载荷下的应力响应。

本文采用数值模拟方法，构建打孔管道接管、补板和套管焊接修复的有限元模型，对修复管道在内压载荷作用下的应力状态进行分析。比较修复结构的应力状态、屈服压力、极限压力，研究修复结构尺寸效应对修复管道承载能力的影响，得到较优的修复方法和修复结构的最佳尺寸。

1 有限元分析方法及模型

1.1 材料模型

管道与修复材料均采用X65管材，采用Ramberg-Osgood(R-O)本构模型表示材料的应力与应变的响应。

(1)

式中：E为弹性模量；ε为应变；σ为应力，σs为屈服应力；α为硬化系数；n为硬化指数。

采用传统单轴试验对管材的应力和应变关系进行测量，再利用R-O材料模型拟合出管材的应力应变曲线(如图1)。管材的力学性能如表1。

图1 管道R-O模型应力应变曲线

1.2 几何模型与网格划分

取管道直径720 mm、壁厚9.2 mm。因管道结构沿轴向与环向对称，故建立1/4几何模型。由于修复结构和管道打孔处均存在一定程度的应力集中，因而采用SOLID90单元对该区域网格进行精细加密划分，而管体其余部位网格适当加大，以达到在保证精度的前提下，优化模型、加速计算的目的。模型加载上对修复结构分步施加内压，最大内压为15 MPa。为了避免模拟过程中产生刚体位移，确保模拟的有效性，在模型的对称面施加位移约束。

2 应力分布分析

2.1 接管修复结构

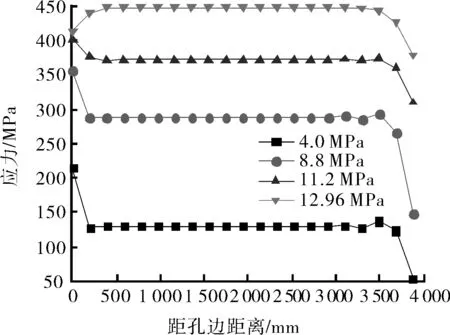
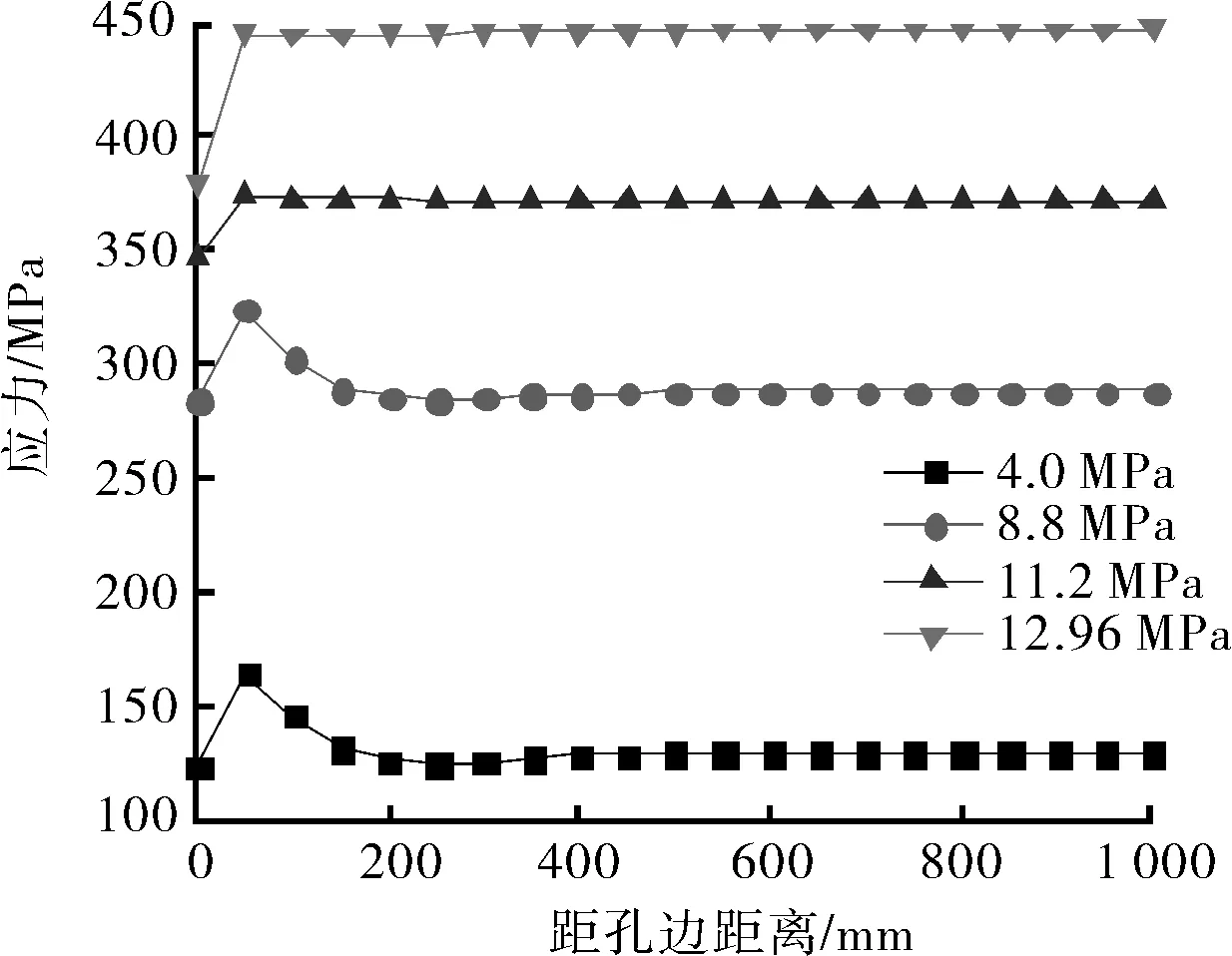
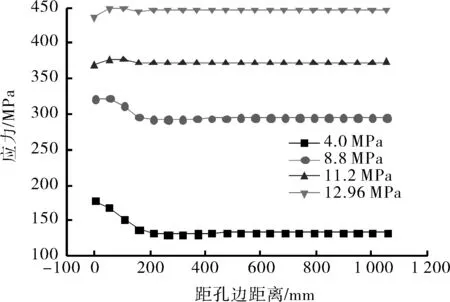
为研究接管修复结构应力与内压的关系，分别沿修复结构的轴向与环向设置2条关键线(如图2)。当内压分别为4.0、8.80、11.20、12.96 MPa时，2条关键线上各点应力如图3所示。

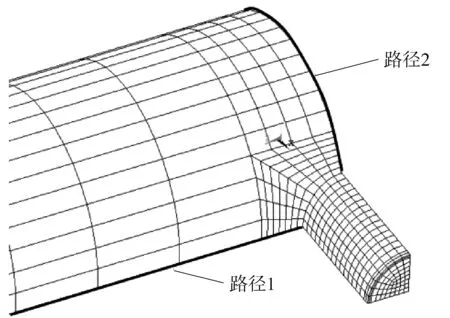
图2 接管模型研究路径

a 路径1

b 路径2

由图3可知，接管内部的等效应力分布不均，接管之外，随着与孔口距离的扩大，管体等效应力逐渐呈均匀分布。穿孔边缘处、接管与管道连接处的应力相对较高，存在应力集中的现象。

8.8 MPa内压水平下接管修复结构的应力云图如图4。接管与管道连接位置应力分布不均，最大等效应力位于该处，管体上其余部位应力分布均匀，接管的应力状态明显小于管体的应力状态。随着内压增加，连接处最先达到材料的屈服应力，进入局部屈服状态，但因为局部发生屈服时，管体整体应力水平不高，整体未发生变形。随着内压的提升，整个修复结构的应力状态加大，达到整体屈服状态，此时的修复结构整体变形较大。管体达到拉伸强度所对应的内压即为极限内力。

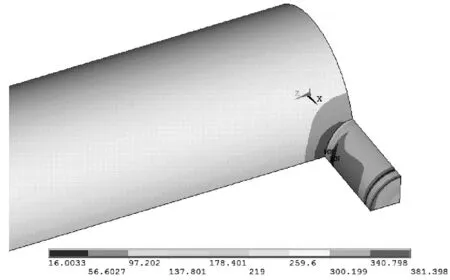
图4 压力8.8 MPa对应的等效应力云图

管道的压力与等效应力关系如图5，管道的屈服内压为8.8 MPa，极限内压为12.96 MPa。

图5 接管修复结构的屈服内压

2.2 补板修复结构

为研究补板修复结构应力与内压的关系，分别沿修复结构的轴向与环向设置2条关键线(如图6)。内压载荷选取与接管修复结构相同，得到关键线上各点的应力分布如图7。

图6 补板模型研究路径

由图7可知，补板内沿轴向与环向的等效应力散布不均，应力最大点位于穿孔边缘；沿管道轴向补板内外管道的应力相差不大，沿管道环向补板内外管道的应力相差较大。2条关键线上各点的等效应力随着与孔口距离的扩大，逐渐呈均匀分布。

b 路径2

当内压为11.2 MPa时，管体等效应力如图8所示。距补板0.65 m、补板与修复管道接触的45°至90°区域应力较高，选取该范围内的点作为确定补板修复管道极限载荷的研究对象。补板修复结构内压与等效应力关系如图9所示，补板修复结构的屈服内压为10.04 MPa。

图8 压力11.2 MPa对应的等效应力云图

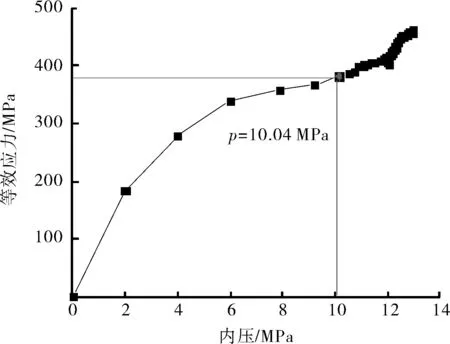
图9 补板修复结构的屈服内压

2.3 套管修复结构

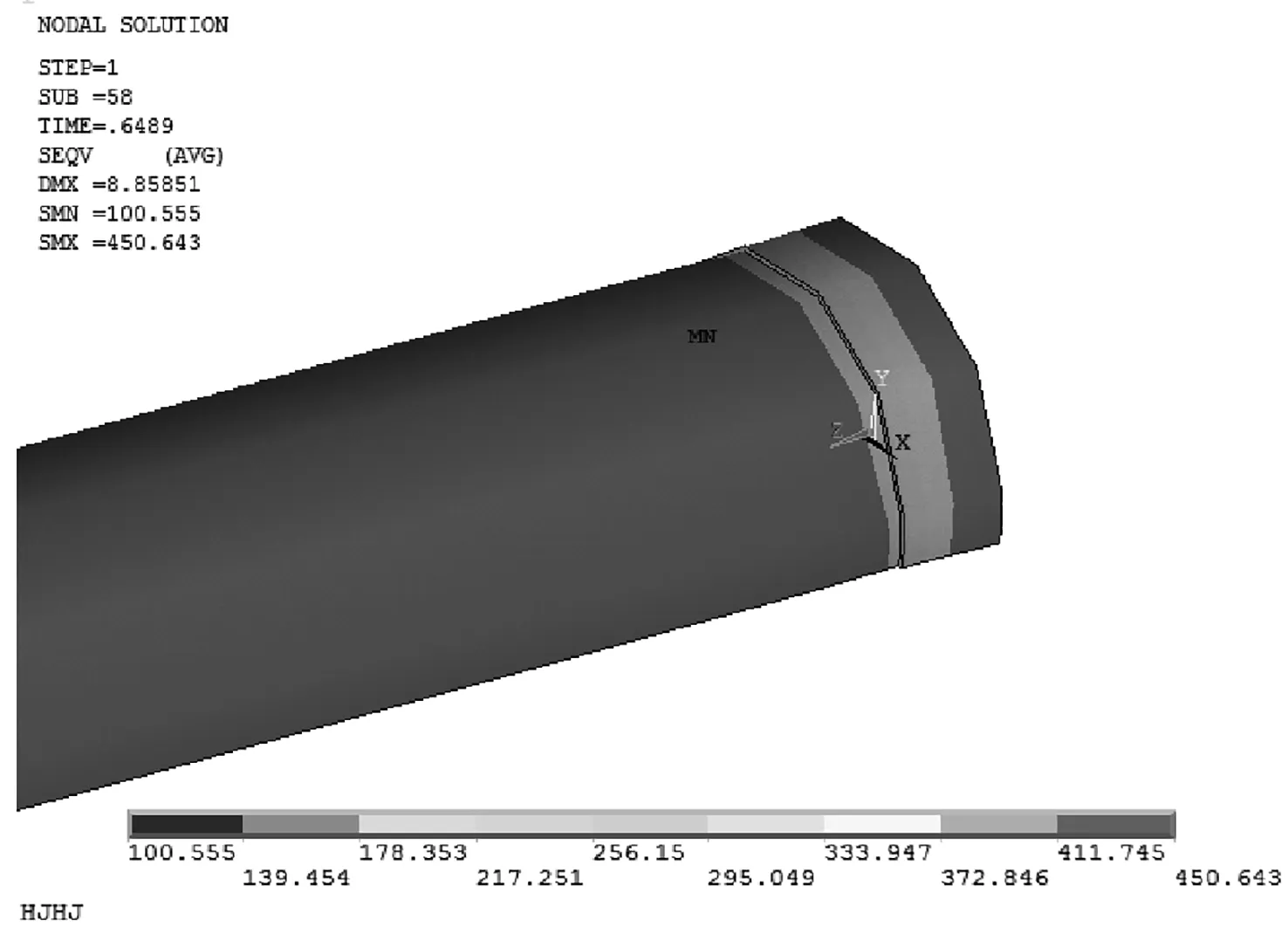
套管修复结构分为管道上存在穿孔和缺陷2种情况。套管壁厚与管道壁厚相同，套管的长度比穿孔或缺陷的长度大100 mm。套管修复结构有限元模型如图10。当修复结构达到极限状态时，管体等效应力云图如图11所示，与修复穿孔管道相比，套管修复缺陷管道时，套管所受等效应力明显较小。当修复结构管体的等效应力达到材料的屈服应力(380 MPa)时，所对应的管体内压作为修复结构的屈服压力。

a 管道穿孔

b 管道缺陷

a 管道穿孔

b 管道缺陷

a 穿孔模型

b 缺陷模型

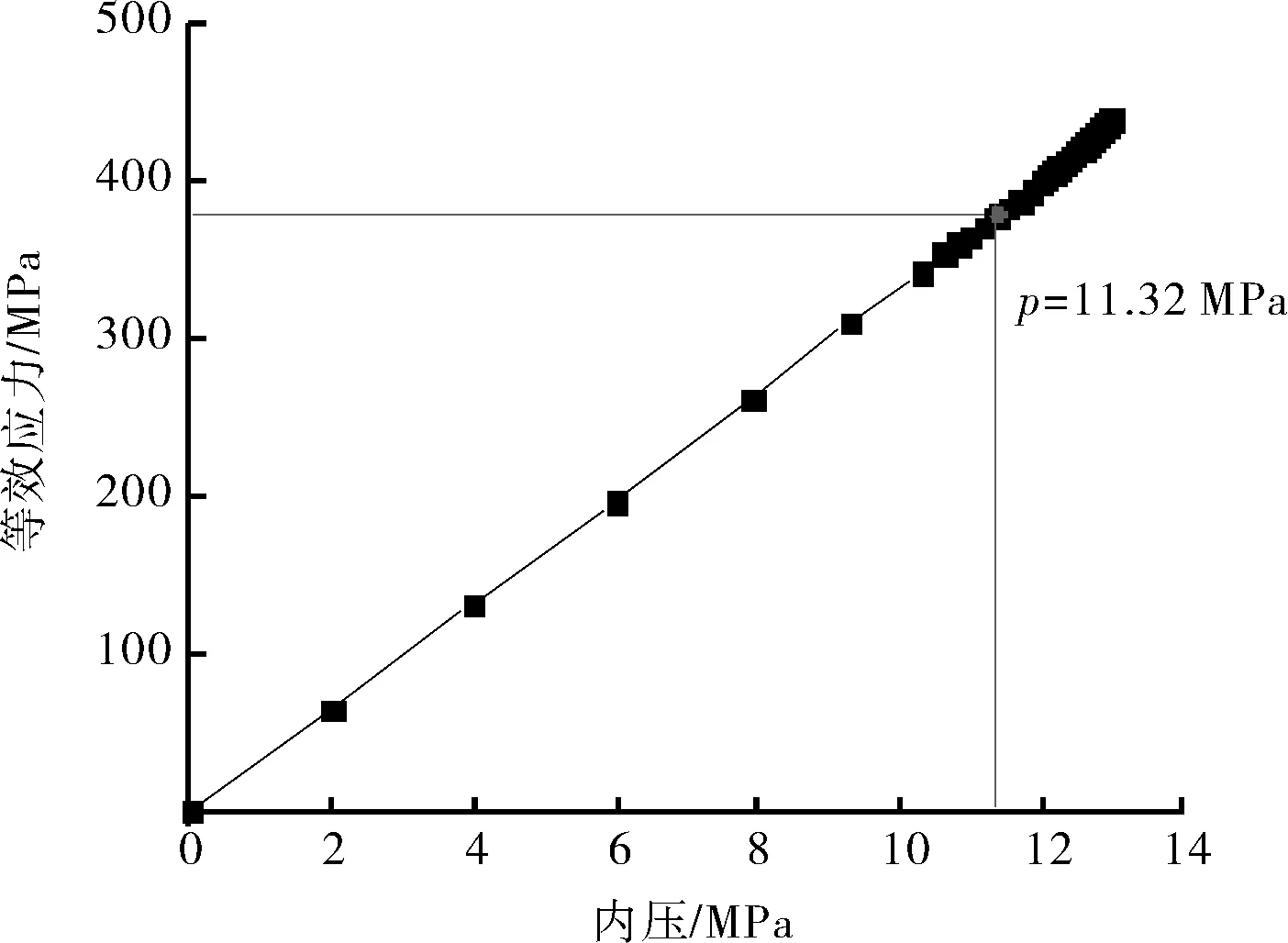
套管修复结构第1个达到屈服应力点的等效应力随内压变化关系如图12所示。在此条件下，穿孔修复模型和缺陷修复模型的屈服压力分别为11.0、11.32 MPa。因此，在同等条件下，套管修复结构修复缺陷的效果要比修复穿孔的好。

3 修复结构尺寸影响分析

3.1 接管修复结构

为研究几何效应对结构修复效果的影响，保持管体和穿孔的几何尺寸不变，模拟接管壁厚为9.2 mm，修复结构的外径取160、210、260、310 mm；取接管外径为250 mm，壁厚7.2、9.2、11.2、13.2 mm，分别进行模拟。

接管修复模型改变参数后所计算得出的屈服和极限压力如表2。对比分析数据可知，在一定范围内改变接管直径不会影响修复结构的极限压力；在接管壁厚确定的条件下，修复结构的屈服压力随接管直径的减小而逐渐增大。因此，对于接管修复结构，一定范围内接管直径越小，结构的承载能力越强。当接管的直径保持一定，修复结构的屈服压力随着接管厚度的增加而增大，即承载能力越强，而极限压力受接管厚度影响较小。所以在确定接管壁厚时，应让其与原始管道相同。

表2 变参数接管模型的极限载荷与屈服应力

3.2 补板修复结构

为研究补板尺寸对修复结构承载能力的影响，保持管道尺寸和穿孔尺寸一定，分别模拟补板的厚度为9.2 mm时，补板边长为50、80、100、130 mm；以及补板边长为100 mm时，补板壁厚壁厚分别取7.2、9.2、11.2、13.2 mm。模拟得到内压载荷为11.2 MPa时，补板修复结构的等效应力。

表3为4种补板边长与4种补板壁厚下模型的屈服与极限压力。当补板的厚度恒定时，补板修复结构的承压能力随补板边长的增大而逐渐减小；当补板边长恒定时，补板的厚度越大，补板修复结构的的承压能力越好；两者相比，补板边长对承载能力的影响高于补板壁厚对承载能力的影响；补板边长和壁厚对修复结构的极限压力没有太大影响。因此，选择补板的几何特征时，补板长度应选取较小的尺寸，补板厚度应与原始管道相同。

表3 变参数补板修复方法的屈服压力与极限压力

3.3 套管修复结构

套管的几何尺寸对修复效果有重要影响，套管太大在实际工程应用中不易安装，套管太小则无法达到预期效果。对于套管修复穿孔和缺陷2种情况，分别模拟套管厚度固定为9.2 mm，套管长度为80、130、200和300 mm；以及套管边长等于200 mm，套管壁厚为7.2、9.2、11.2、13.2 mm 4种情况。

表4为套管修复穿孔和修复缺陷时，改变套管长度和厚度所得到的屈服承压能力。在同等厚度条件下，套管的长度对修复结构的屈服压力影响不大；采用套管修复穿孔时，在同等长度条件下，修复结构的屈服压力随套管的壁厚增加而提升；采用套管修复缺陷时，在同等长度条件下，修复结构的屈服压力不随套管壁厚而改变。