基于柔性神经网络和转矩分配函数的SRM控制
2020-08-01李红伟唐学建胡其杰
张 锟,李红伟,唐学建,胡其杰,陈 琦
(西南石油大学 电气信息学院,成都 610500)
0 引 言
与传统普遍应用的直流、交流电机相比, 开关磁阻电机(SRM)具有结构简单、工作稳定、性价比高等优点,越来越引起人们的关注,在新能源电动车[1-2]、煤矿机械[3]、油田抽油机[4]等系统中得到了一定的推广应用。但是, SRM是双凸极变磁阻电动机,基于该结构产生的磁场分布呈严重非线性,同时,其开关式换相供电的工作原理使得它运行(特别在较低转速运行)时会产生较大的转矩脉动。转矩脉动会导致较大的振动,从而缩短电机寿命;转矩脉动也会产生较大的噪音,这大大限制了SRM的实际应用[5]。
为了减少电机转矩脉动,国内外学者做了大量的改进,也取得了许多较有效的研究成果。一方面是从开关磁阻电机的机械结构入手[6-7],优化定子结构,使得电机的电磁、电感分布更加合理;另一方面采用更先进的SRM的控制策略[8-14],如当前讨论较多的转矩分配函数法[9-11]、微步控制方法[12]、直接瞬时转矩控制[13]、神经网络控制[14]等。
采用传统常规的SRM控制方法时,由于控制策略相对简单,在SRM的绕组换相控制系统开通和关断相电流时,下一相电流开通产生的转矩不足以支持上一相电流关断的减小量,这就产生了较大的转矩脉动。转矩分配函数法(Torque Sharing Function, TSF)是一种抑制SRM转矩脉动较为理想的方法,易于实现且转矩脉动抑制效果明显,故在SRM控制领域得到了广泛应用[9]。文献[9]提出了一种通过TSF在线修正的DITC。在电机运转时,在换相前和换相后分别对转矩进行补偿,从而减小换相阶段合成转矩的脉动。但是随着电机转速的升高,系统难以精确跟踪换相阶段补偿的时机。文献[11]基于这一问题提出了一种改进型TSF的转矩脉动抑制方法。转矩下降阶段关闭所有开关管使其快速下降,再用期望转矩减去实时转矩的值作为下一阶段的转矩给定,使其补足上一相跌落的转矩。
神经网络控制也是目前研究较多的控制,文献[14]提出了自适应神经网络控制算法实现开关磁阻电机调速控制。但神经网络控制的激活函数确定后,使整定权值变为一个,降低了精确度。
本文借鉴TSF,结合神经网络控制,外环采用PID控制器对速度进行调节,内环采用柔性神经网络(Flexible Neural Network, FNN)对转矩偏差及电机的建模误差进行修正,在Matlab/Simulink环境下,建立了柔性神经网络结合转矩分配函数的开关磁阻电机瞬时转矩控制的仿真模型。
1 开关磁阻电机的数学模型
SRM具有双凸极机械结构,运行时各相依次通电,这使得SRM控制系统是一个强非线性控制系统。基于机电能量转换原理搭建SRM的数学模型[15],即根据电磁感应定律,针对第k相有:
(1)
式中,ek、ψk分别为第k相的感应电动势、磁链。
基于微分方程描述开关磁阻电机构成的机电系统,可分为电路方程、机械方程、机电联系方程3部分[16]。
1.1 电路方程
基于SRM的各相通电回路可以得到第k相绕组的电压平衡方程式为
(2)
式中,Uk、Rk、ik分别为第k相的外加电压、电阻、电流。
ψk与ik和转子位置有关,即
ψk(θ,ik)=Lk(θ,ik)ik
(3)
联立式(2)、式(3)可得:
(4)
其中,式中第一项为电阻压降;第二项为变压器电动势;第三项是运动电动势。
1.2 机械运动方程
转子机械运动方程式:
(5)
(6)
式中,J为转动惯量,D为摩擦系数,Te为电磁转矩,TL为负载转矩。
为了更准确的构建SRM的模型,根据所采用的电机参数(如表1所示),可基于有限元分析方法在Ansys平台上建模仿真得到L-i-θ和T-i-θ的静态数据,如图1和图2所示。基于得到的静态数据和电路方程、机械运动方程可以建立较精确的SRM的模型[17]。
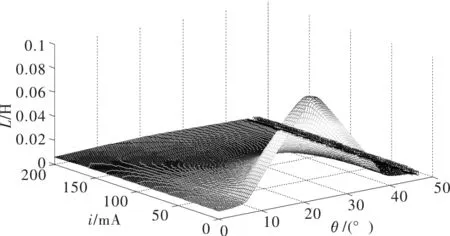
图1 L-i-θ关系曲面

图2 T-i-θ关系曲面
2 柔性神经网络
2.1 S型函数
柔性神经网络是一种包含柔性、S 型函数参数可变的网络[18]。它与普通神经网络不同的是其S型函数是可以变化的,其参数可以不断自行调整,最终达到适应整个系统的参数,其自由度比普通神经网络自由度更高,控制精确度更高。
S函数可分为单极性和双极性[19-20],分别如下:
(7)
(8)
式中,α为函数整定参数,x为输入变量。
一般单极性函数训练时间较长,且容易得出局部最优,降低了精确度[20],所以本控制系统选择双极性S型函数,分别对x和α微分得到:

(9)
(10)
2.2 学习算法
神经网络主要由:输入层,隐藏层,输出层构成。柔性神经网络控制除了需要对各层连接权进行调节外,还需要对α参数进行调节,故涉及两个学习算法。
对连接权的算法与神经网络算法一致,用BP算法规则[21]即可。此处着重介绍双极性S型函数参数α的学习算法:
系统采用典型的三层BP神经网络,关系式为
Y(n)=[v1,v2,…,vm…vM]
(11)
其中,
vm=g(um(n))
(12)
式中,Y(n)为实际输出,vm为第m个神经元的输出,n为迭代次数,M为输出层神经元总个数。
网络的期望输出为
d(n)=[d1,d2,…,dM]
(13)
则第m个神经元的误差信号为
em(n)=dm(n)-Ym(n)
(14)
误差总能量为
(15)
(16)
式中,η为优化步长,即学习率,且η>0。对输出层,根据微分的链式规则,有:
(17)
e(n)是em(n)的二次函数,其微分为一次函数,即
(18)
则化简得到
(19)

(20)
其中,0 FNN的学习过程分为两个阶段:第一阶段,根据所有的输入量决定隐含层各节点的柔性激活函数的参数α;第二阶段,当α参数确定即激活函数确定后,根据输入量,求出隐含层和输出层之间的权值ωi;并且可在完成第 2阶段的学习后,再根据学习样本数据,反馈再修正α,以进一步提高网络的精度。 SRM是双凸极结构,产生的磁场分布呈严重非线性。其采用开关式换相供电,这使得传统控制算法(如PID控制)无法有效、精确的控制电机。本文在基于转矩分配函数的直接转矩控制策略的基础上,引入了FNN智能控制算法。 基于FNN网络的SRM的DITC系统框图如图3所示。 图3 系统结构图 双闭环控制系统主要包括速度外环和转矩内环。速度控制器(PID环节)、转子位置检测、速度检测构成速度外环;转矩分配模块、转矩滞环控制模块、转矩估算环节、转子位置检测模块构成转矩内环。除此之外,系统还包含电机本体、功率变换器等环节。 系统输入为给定转速ω+,其与反馈转速ω*的偏差Δω作为PID环节的输入,输出参考转矩Tef1经FNN环节得到最优参考转矩Tef,经过转矩分配模块得到三相绕组瞬时参考转矩TAef、TBef、TCef;转矩滞环控制环节的功能是将三相瞬时参考转矩和经过转矩估算环节反馈的实时转矩做差,再根据转矩差决定功率变换器件中A、B、C三相各相的开通和关断。这样就构成了转矩和转速双闭环,实现简单,达到抑制转矩脉动的目的。 电机绕组开通时产生的转矩增加量小于相绕组关断时的转矩减小量,这样使得合成转矩会有较大落差,故形成转矩脉动。DITC以瞬时合成转矩为控制目标,通过TSF分配瞬时时刻每一相的期望转矩,再通过转矩滞环控制和转矩估计形成转矩闭环控制,使得瞬时合成转矩跟踪瞬时期望转矩,实现均衡换相,抑制转矩脉动。 转矩分配模块的核心为转矩分配函数,TSF的作用是根据转子位置角信息,将转速输出的期望合成转矩分配成各相的相参考转矩,各相转矩和总转矩之间满足: (21) 式中,fi(θ)为第i相绕组的转矩分配函数,m为电机的相数,Ti为第i相参考分配转矩,Tef为期望合成总转矩。TSF的种类多种多样,常见的TSF有直线型、余弦型、指数型及立方型等。本系统设计目的是最大限度减小转矩脉动,根据这一特征系统选择余弦型作为分配函数。 在一个转子角周期内,第i相的正弦型转矩分配函数表达式如: (22) 式中,θon为电机相绕组开通角;θoff为转矩分配函数中相绕组开始减小电磁转矩所对应的转子位置角;θov为TSF中电机绕组中相邻两相同时导通的叠角度;r为转子角周期。其中两相相绕组的电流重叠角应该遵循如下要求: (23) TSF的余弦波形图如图: 图4 TSF余弦波型图 从图4中可以看出,根据TSF的规则:当转子位置角在相电流重叠区域外时,只有一相绕组处于导通激励状态。在相电流重叠区域,余弦型TSF为转矩分配模块相邻两相的转矩随转子位置角做余弦性的增长和减小,当前关断相呈余弦性减小的同时,当前开通相以同样的比率增加,使得合成的瞬时转矩恒定。在其余三种转矩分配模块下,导通相的转矩增加和关断相的转矩减小按相应TSF波形合成恒定的瞬时转矩。 对于三相12/8极SRM来说,余弦型转矩分配函数在一个转子角周期内,三相转矩分配情况如下: 图5 基于余弦型TSF的SRM三相转矩分配图 图中Tk、Tk-1、Tk+1分别表示SRM当前相绕组转矩分配、前一相绕组转矩分配以及后一相绕组转矩分配,其数学模型可用下面式子表示: (24) Tk-1=Tref-Tk (25) Tk+1=0 (26) θov=θoff(k-1)-θon(k) (27) 系统根据转子位置估算模块得到SRM位置信息角,在得到参考转矩TAef、TBef、TCef后,使得SRM各相转矩都能跟随参考转矩进行有效控制,从而抑制合成瞬时转矩脉动的幅度。要实现对转矩的准确控制,对提高系统抑制转矩脉动效果是至关重要的。 为了验证系统的可行性,在Matlab/Simulink环境下对整个系统进行建模仿真。其中电机参数如表1所示,设定转速为150 r/min,负载设定为20 N。 表1 电机参数 为了对比,还搭建了一个常规的TSF直接转矩控制SRM控制系统和单纯的神经网络控制下的直接转矩控制的SRM控制系统。 图6~图8为系统仿真运行的转速曲线图。 图6 柔性神经网络直接转矩输出转速 图7 转矩分配函数直接转矩输出转速 图8 柔性神经结合转矩分配函数输出转速 从上面3个转速结果图我们可以看出,3个控制系统均能大致达到设定转速150,并能在短时间能达到稳定,说明3种控制均能达到基本运行。对比可以得出,柔性神经网络控制下的电机转速达到稳定需要0.05 s左右,无超调;基于TSF的DITC下达到稳定需要0.011 s,超调达到了6.5%;柔性神经结合转矩分配函数控制转速达到稳定需要0.01 s,超调也只有3.3%,基本无影响。第3种控制系统结合了柔性神经网络的低超调特性和TSF的快速稳定特性,使SRM性能得到提升。 本文设计的目的是为了减小开关磁阻电机的转矩脉动,其结果分别如图9~图10所示。 图9 柔性神经网络直接转矩输出转矩 图10 转矩分配函数直接转矩输出转矩 图11 柔性神经结合转矩分配函数输出转矩 由3种转矩结果图我们可以看出,系统运行后能快速达到设定负载的转矩20 N。转矩在达到稳定后会产生周期性脉动,这与电机的双凸极机械结构和换相式供电符合。由图像可得出电机稳定时的转矩图像,由局部放大图得到转矩在一个脉动周期的最大值Tmax与最小值Tmin。为了衡量脉动的大小,电机的转矩脉动进行量化,定义转矩脉动率如: (28) 根据仿真结果的最大值Tmax与最小值Tmin,可以计算出3种不同控制器结合转矩分配函数应用于设计的开关磁阻电机直接瞬时转矩仿真系统的转矩脉动率。如表2所示。 表2 两种转矩分配函数转矩脉动情况 对控制系统进行对比发现3种控制系统的脉动率都小于20%,但基于柔性神经网络结合TSF的改进型DITC脉动率最低至1.28%。 除了电机脉动率还可以直观的看出在相同时间内,柔性神经网络结合TSF的控制系统的脉动个数明显少于前两种,即它的脉动周期比较长,可以大大缓解脉动带来的振动。 对开关磁阻电机而言,柔性神经网络控制和转矩分配函数在抑制脉动转矩上都有较好的表现,但是在仿真和实际应用中都有各自的缺点。本文以PID应用于速度环、柔性神经网络控制结合转矩分配函数应用于SRM控制系统的转矩环,得到了一种抑制转矩脉动的改进控制策略。该策略综合了柔性神经网络和转矩分配函数的优点,仿真结果表明转速稳定响应更快、超调更小;转矩脉动抑制效果远优于其余两种控制。2.3 柔性神经网络的学习过程
3 系统设计
3.1 系统总体设计

3.2 转矩环的设计


4 仿真结果及分析

4.1 转速结果


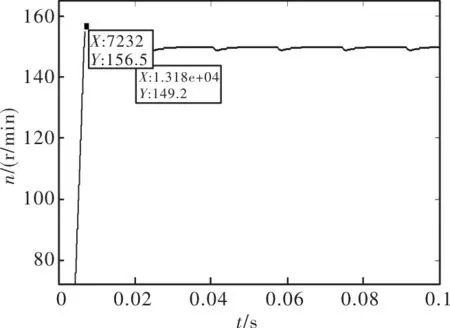
4.2 转矩结果及其分析




5 结 语
