基于遗传算法的非高斯系统随机分布控制

洪越 殷利平

0 引言

工业技术的不断发展一方面使得生产率快速提高，社会不断进步，另一方面工业过程中的不确定因素也使得工业控制越来越复杂，传统的控制理论在很多情况下已经不符合现代工业的发展要求.近几十年来，在控制理论界中有很多面向随机系统的随机控制和随机估计方面的研究[1-2]，其研究成果已经广泛地应用于诸多工业领域，如最小方差控制，它属于随机最优控制的一种特殊情形，具有求解和实现简便的优点.对于线性高斯系统，可以采用最小方差控制等方法[3-4]，但是当系统含有非高斯变量时，使用均值和方差不能完全描述系统的特征，这些方法便不适用.有鉴于此，以PDF(概率密度函数)为控制对象的非高斯随机分布系统控制理论逐渐成为随机控制研究领域的一个新分支[5-6].尽管非高斯随机分布系统控制理论研究意义重大，但是开展非高斯随机分布系统的理论研究是相当复杂的.

在随机分布控制系统中，控制的目标是实现输出的PDF跟踪目标PDF[7-10]，在基于泛函算子模型的随机分布控制系统中，基于数据采用KDE(核密度估计)方法估计PDF具有很多优越性[4].采用KDE估计输出的PDF，根据控制目标建立性能指标函数，并将控制目标转化为性能指标函数优化的控制方法能够大大简化算法程序，并且即使当建模发生误差，由于该算法基于数据特征，因此也不会很敏感.在以往优化性能指标函数时，往往采用的是梯度算法.梯度算法的计算过程复杂，当需要优化的指标函数复杂或者系统本身就很复杂时，算法过程中的求导和泰勒展开比较困难,且计算量大耗时长.因此，在实际应用中寻找到对模型要求低、计算量小，能找到全局最优解的算法是很关键的.现代智能算法大多来源于生物智能或者物理现象，虽然在理论上还不完善也不能确保找到解的最优性，但是它符合非高斯随机分布系统的优化要求，即对模型要求低、搜索全局化、鲁棒性强且高效.

遗传算法最早由美国的Holland教授提出，它来源于20世纪60年代自然与人工自适应系统研究的一种模拟生物的遗传和进化来解决最优化的搜索启发式算法[11].遗传算法具有较强的灵活性，能够通过稍加调整以适应实际待解决问题.遗传算法由于其特殊的搜索特性，对优化问题没有太多的数学要求，且具有有效地进行概率意义的全局搜索的能力.作为一种智能算法，在工业生产中遗传算法可以用来优化性能指标函数，通过种群个体的遗传操作、交叉操作和变异操作不断更新优化种群，最终找到最优解，即最优控制输入.

本文根据随机分布相关控制理论，基于数据采用KDE估计输出PDF，并建立性能指标函数，采用遗传算法对性能指标函数进行优化，找到最优控制.以磨矿系统为例进行仿真实验，以证明所提方法的有效性.

1 系统模型

本文考虑一个工业上的模型——磨矿系统模型，该模型的控制目标是：在每一个时刻，系统输出PSD(粒度分布)跟踪一个目标PSD.本文用PDF表征PSD，二者可视为等价.选矿是矿产品生产过程中最重要的环节，而磨矿又是选矿中动力和金属材料消耗最大的一个阶段[12].磨矿回路是一个非常复杂的非线性系统，为了提高资源利用率，提高矿料研磨后的磨矿作业指标是一项富有挑战性但是非常有意义的任务.

图1所示为磨矿结构回路，考虑较为普遍的湿磨情况，在工作过程中研磨机和蓄液池都需不断加入水.其中水力旋流器的作用是在离心力和重力的作用下使质量大的矿物颗粒与质量小的矿物颗粒分离，质量大的成为底流矿料通过沉沙口再次进入研磨机，质量小的随溢流排出.同时新添矿料通过进料器添加到研磨机内，研磨后的矿物颗粒通过排矿口进入蓄液池，蓄液池的悬浮液由水泵抽入水力旋流器[13].

设磨矿系统模型为

(1)

其中k表示的是系统生产过程的采样时刻，uk是控制输入序列，即磨矿机新添矿料量，yk是受控输出序列，即磨矿系统输出的随机粒度，xk是系统的状态序列,即磨矿系统磨矿浓度，ωk和vk是非高斯随机输入序列，即磨矿过程中不确定因素引起的输入.

在采样时刻k，将系统(1)的输出PDF记为γyk，目标PDF由矿料性质和后续选择方法决定，记为γd，即磨矿产品的PSD[14-15]设定值.在每个采样时刻k，将系统输出的L个溢流产品粒度{yki}(=1,2,…,L)作为样本，采用KDE的方法得到系统输出的PDF，即γyk，根据控制目标建立性能指标函数，使用遗传算法优化性能指标函数得到最优控制uk，使得输出PDF跟踪目标PDF.

磨矿系统的算法结构如图2所示.

2 基于KDE的粒度PDF估算

KDE是一种非参数估计，不需要先验知识和任何概率分布形式的假设，单纯地从数据出发研究样本的分布特征，适合于求取每一采样时刻k流溢产品粒度的PDF.根据KDE原理，γyk(τ)的核密度估计[16-17]为

(2)

其中τ表示为统计学中肯德尔相关系数的值，L为样本容量，h为带宽，起平滑系数的作用，K(·)为核函数，通常选择镜像对称的单峰函数，此处为高斯核函数：

(3)

h=1.06σL-1/5，

(4)

其中σ为样本的标准差.

3 性能指标建立

本文跟踪的目标是一个给定的PDFγd(τ)，控制目标是设计控制律，使输出的条件PDFγyk(τ|xk,uk) 满足：

γyk(τ|xk,uk)→γd(τ),k→+∞ .

(5)

基于泛函算子模型的随机分布控制理论，涉及到的性能指标函数[18-20]一般可以写成：

(6)

式(6)中第1项是统计特性，表示输出PDF与目标PDF之间的距离，可以用积分表示为

(7)

第2项为uk的能力约束项.性能指标函数表达式中Qk，Rk为权系数.

4 基于遗传算法的最优控制策略

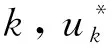
(8)

基本遗传算法由选择算子、交叉算子和变异算子组成，在遗传算法中优化的目标函数即为适应度函数.选择算子中使用比例的方法来计算个体遗传下去的概率，所以要求所有个体的适应度必须不为负.在遗传算法中，个体适应度越大被遗传到下一代的概率越大，个体适应度越小被遗传到下一代的概率越小.本文中所需优化的性能指标函数Jk为优化的目标函数即遗传算法中的适应度函数，Jk不为负，但是优化的目标为求最小值，即所求目标函数为最小，使用下式方法进行转换[21-22]：

(9)

式中Cmax是相对较大的数，选取方法有：1)预先选择一个较大的数；2)进化到当前代为止最大的目标函数的值；3)最近几代群体中的最大目标函数值.

基于遗传算法的非线性非高斯系统的PDF跟踪控制算法的详细步骤可总结如下:

1)初始化磨矿系统(1)的随机状态变量x0和输入控制u0.

2)设采样时刻k=0.

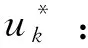
②令t=2；

⑤为了进行交叉运算，将种群个体进行二进制编码操作；

⑨若t>T进入4)否则进入③.

该算法可以用图3表示.

5 仿真

下面将以模型(10)为例，详细阐述怎样采用遗传算法优化性能指标函数，以实现对磨矿粒度PDF的跟踪控制:

(10)

其中，ωk的PDF为

(11)

vk的PDF为

(12)

设磨矿产品的PSD指标为高斯分布N(1,0.252)，即跟踪目标的PDF为

(13)

在仿真中设定的初始条件为x0=-0.1,u0=0.1,权系数取为Qk=15，Rk=0.1.通过多次测试，在遗传算法中种群的个体个数为30，迭代的次数T=10，杂交率= 0.7，选择率= 0.5，变异率= 0.1.本仿真中采用式(9)的方法，取Cmax=30,即：

(14)

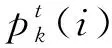
与遗传算法相似，粒子群算法也是属于进化优化算法的一种，它源于对鸟群捕食行为的研究.对于粒子群算法系统初始化仍为一组随机解，以适应度函数为评价标准，在算法中将每个优化问题的解看作是一个粒子，通过粒子速度的改变找到粒子最优位置即系统最优解.在粒子群优化算法中粒子位置的更新与速度的更新都具有良好的导向性，因此粒子群对空间中的最优解有很强的逼近能力，且收敛速度快，但是这种导向性很容易导致该算法出现陷入局部最优解的情况，全局搜索能力弱.于是在复杂的工业问题中，遗传算法相比于粒子群算法更具实际应用的适应能力.

6 结论

本文以磨矿系统为例，将适当调整后的遗传算法应用于PDF的控制算法中，通过调整每一采样时刻的磨矿机新添矿料量，控制系统的输出.首先在每一采样时刻k，用KDE估计磨矿产品粒度的PDF，然后根据控制目标基于输出PDF和目标PDF的误差建立性能指标函数，最后用调整后的遗传算法优化性能指标函数，实现最优控制.仿真结果表明，在实际应用中，遗传算法进行小的调整后就能够适应模型的要求，实现随机分布控制系统的控制目标.