基于线性编码补偿方法的非固定丢包率下的分布式融合估计器

韩旭，赵国荣，王康

（1.中国人民解放军91001部队，北京100036； 2.海军航空大学 岸防兵学院，烟台264001）

网络化多传感器融合估计因其在航空航天、无人运载器导航和网络化控制等领域的重要应用，已经引起了国内外学者的广泛关注和研究［1-5］。在实际的应用系统中，不可避免地存在模型的不确定性、数据丢包问题，导致处理中心得不到正确完整的测量信息，使得融合估计性能受到严重损害。

学术界在设计状态估计器时就如何补偿丢包损失已经有了一系列成果［6-10］。文献［6］提出1种常增益的算法，用估计值反馈代替丢失的测量信息，避免了在线计算的负担。文献［7］提出1种线性预测器，对已经到达处理中心的测量值进行加权处理，并给出最优加权系数和最优阶数的获取方法。文献［8］提出1种指数衰减加权系数方法，通过调节加权系数得到满意的估计精度。然而文献［6-8］均考虑在处理中心处对丢包信息进行补偿，虽取得了不错的精度，但这些方法所用的补偿值均是对已经到达处理中心的测量信息进行组合，而没有重新利用已经丢失的数据，精度的好坏取决于系数的选取。对此，文献［9］指出无论是在单传感器估计还是在多传感器融合估计中，在传感器端计算得到状态估计并将其发送至远程中心，能够补偿之前所有丢失的测量值，但是状态估计值的维数往往高于测量值的维数，这就意味着传输估计值会占用更多的网络带宽或者网络资源，这可能会导致更高的丢包率。为了降低数据传输的维数并且严格补偿丢包损失，文献［10］研究单传感器状态估计问题时提出在发送数据之前对存储在传感器存储空间中的之前的有限个测量值进行线性组合，进而得到新的传输量后传输至处理中心，基于该传输量得到Kalman滤波器，提高了估计精度。然而当系统模型存在非高斯非白噪声随机干扰时，文献［10］中方法不再适用，并且文献［10］没有给出离线估计器的设计，其估计器增益和误差协方差均需根据每一时刻的丢包情况进行实时计算，若拓展到多传感器融合估计器，高维矩阵的实时求逆计算不利于实时性要求高的场景。

另一方面，目前学术界在设计具有随机丢包的多传感器状态估计器时，均假设信道的丢包率是固定不变的。然而在某种实际网络环境中尤其是无线网络环境中，信道的丢包率与同时访问信道的传感器数量是相关的［11］。非固定丢包率目前在网络化多传感器状态估计中并没有得到广泛重视和研究。仅文献［11］以CSMA／CA标准通信协议为研究对象，给出无线信道丢包率与同时访问网络的传感器数量之间的函数关系，在集中式框架下给出了2种次优的融合估计器。该方法有如下不足：没有考虑模型不确定性；未对丢包损失进行有效补偿；集中式融合结构虽能保证现有测量信息精度损失最小，但是其容错能力较差，工程上难以实现；传感器传输概率优化需进行高维矩阵求逆，不利于实时性。

考虑到文献［11］的上述不足，本文在分布式融合框架下，研究具有模型不确定和非固定丢包率的多传感器融合估计器设计问题。其中模型的不确定性描述为系统矩阵受到非高斯非白噪声随机扰动，无线信道的丢包率与传输数据包的传感器数量成正比，为补偿丢包带来的损失同时降低网络带宽的占用，利用文献［10］中线性编码方法，每个传感器将过去测量得到的有限个测量数据进行线性组合，得到新的传输量后经无线信道传输至远程处理中心。针对随机到达的各个传感器对应的新的传输量，本文设计一种最小方差离线局部无偏估计器，该估计器便于离线计算并利用数据包到达变量，利用最优线性无偏估计方法［12］得到最小方差意义下的分布式融合估计器，建立融合估计误差协方差与各传感器每一时刻传输概率之间的关系，在编码参数确定的前提下，可通过设计各传感器的传输概率使得融合估计器达到满意的性能。

1 问题描述与分析

考虑如下离散不确定线性随机系统：

假设系统由N个传感器进行观测，第i个传感器测量方程描述为

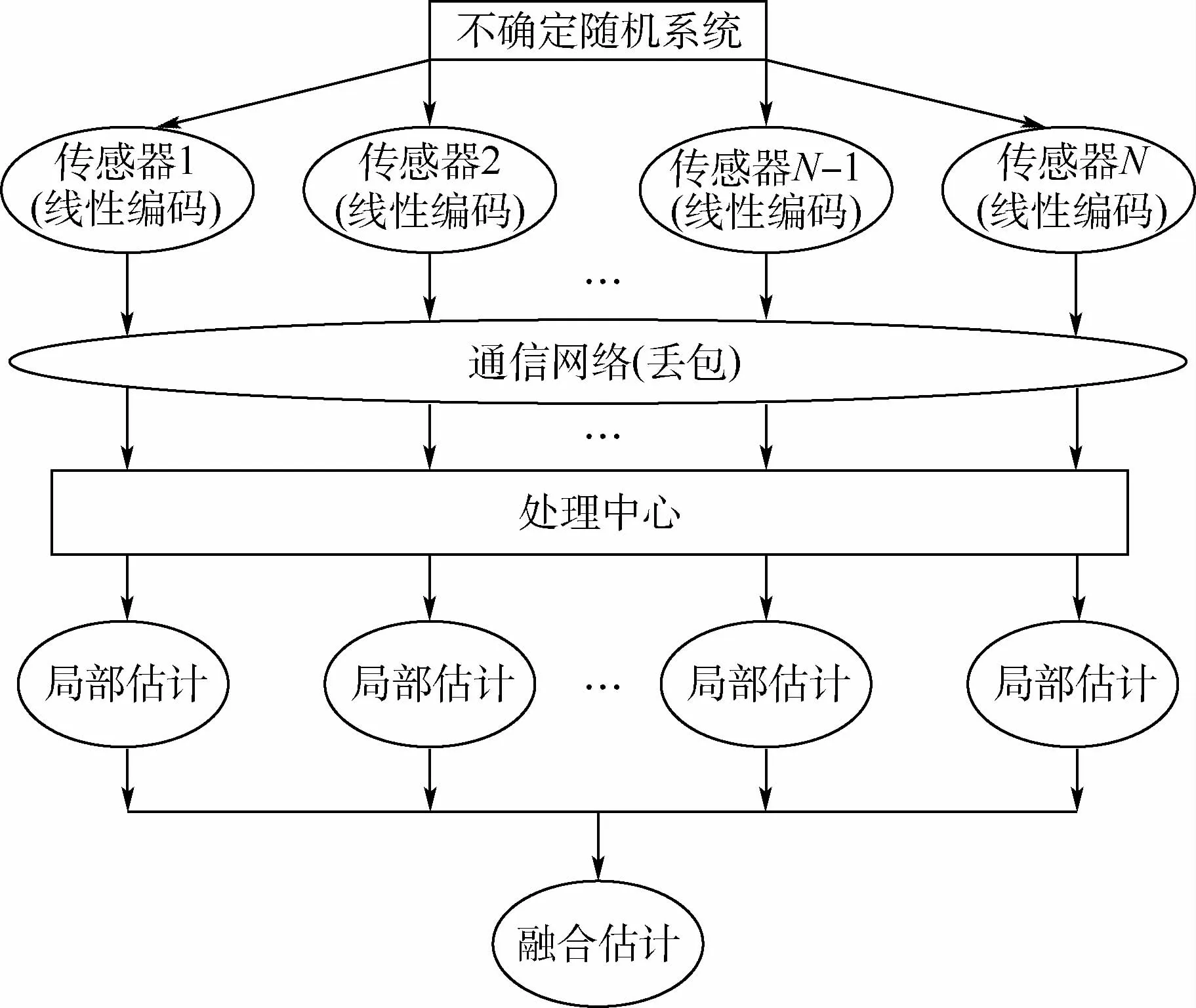
图1 网络化分布式融合估计结构Fig.1 Networked decentralized fusion estimation structure

接下来本文基于式（9）、式（12）和式（13）设计局部最优估计器。目前在研究模型不确定性的文献中，大多假设系统矩阵中的随机噪声为高斯乘性白噪声，并且可以将系统矩阵中的白噪声转化为系统噪声，因而可直接利用文献［10］中标准Kalman滤波方法得到状态估计。而在方程（12）中，因为矩阵Φik中存在乘性随机噪声gk，使得每一时刻系统矩阵不再是确定的，并且未假设gk是白噪声，所以标准的Kalman滤波方法不再适合解决系统方程式（12）、式（13）的最优估计问题，需要设计估计方法。为此本文采用如下估计器形式：

2 局部估计增益设计

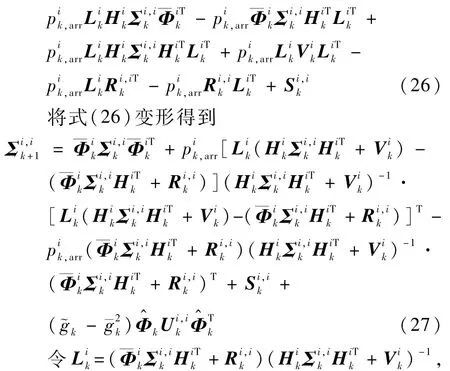
即式（21），此时式（27）最小，即得到式（22）。同理可得到式（23）。 证毕

需要说明的是：一方面，与文献［10］中线性编码后的Kalman估计器相比，本文设计的局部估计器（式（14））处理了模型不确定性，并且得到的局部估计器增益（式（21））及局部估计误差协方差矩阵（式（22））均可离线计算，从而使得融合估计器（式（19））可离线计算，提高了实时性。另一方面，式（14）中（）一项可视为局部新息项，该局部新息项引入了随机变量。其意义在于：当并未达到处理中心即＝0时，新息项为0，离线估计增益不起作用。若按照文献［14］中在设计估计器的新息项将丢包变量用其概率代替，其后果是当＝0时，局部新息项不为0，而局部估计增益不为0，则此时反而引入了局部估计误差。

3 次优传输概率设计

4 算例仿真

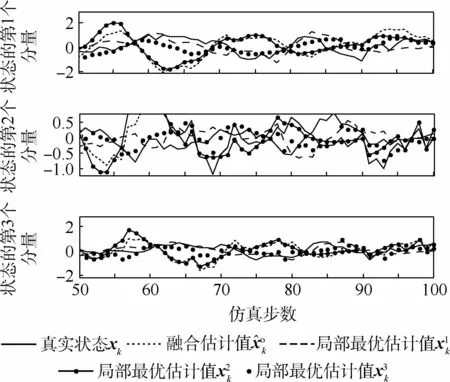
图2 真实状态、融合及局部最优估计值计算结果Fig.2 Calculation results of true state，fusion and locally optimal estimates

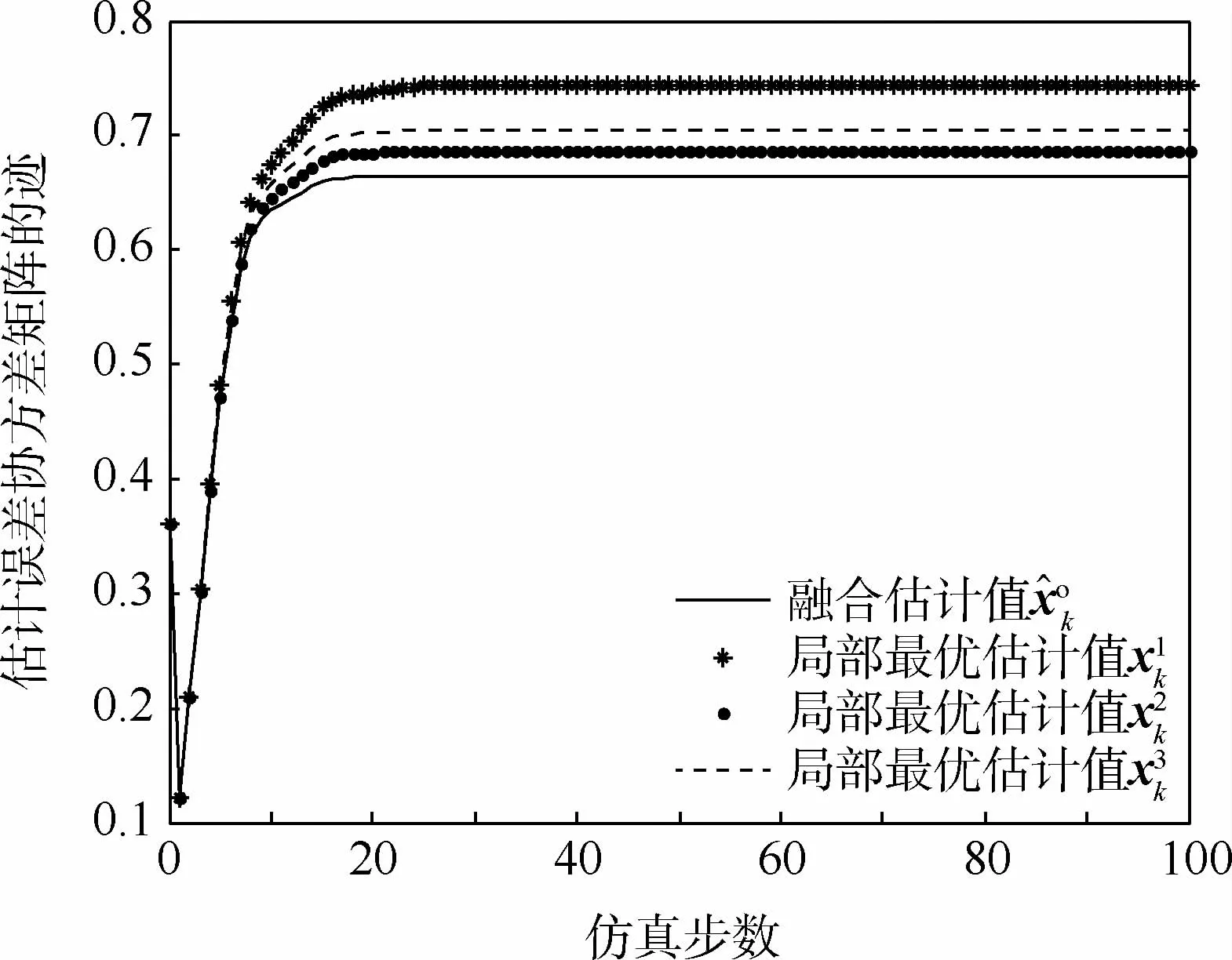
图3 估计误差协方差矩阵的迹计算结果Fig.3 Calculation results of trace of estimation error covariance matrixes

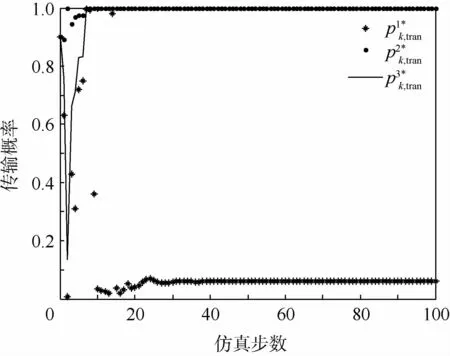
图4 次优传输概率计算结果Fig.4 Calculation results of suboptimal transmission rates

表1 不同传输概率下的融合估计精度Table 1 Fusion estimation accuracy with different transmission rates

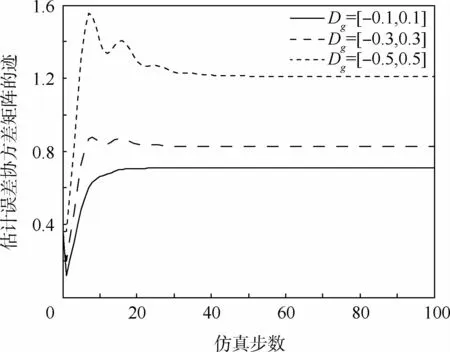
图5 乘性噪声与融合估计精度的关系Fig.5 Relationship between multiplicative noise and fusion estimation accuracy

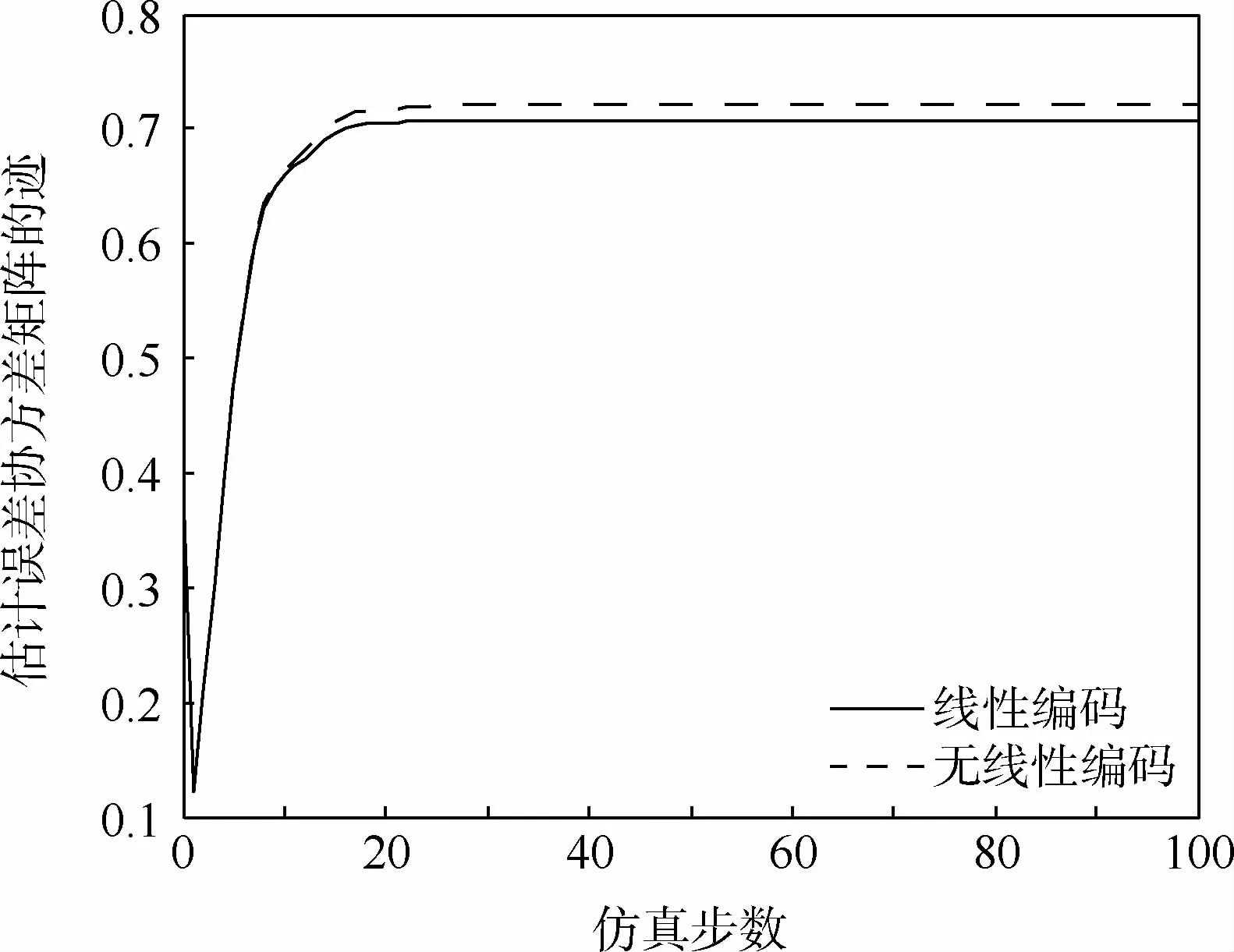
图6 线性编码对融合估计精度的影响Fig.6 Effects of linear coding on fusion estimation accuracy

5 结束语

本文利用线性编码方法对非固定丢包在发送端进行补偿，降低了信息损失；建立了分布式融合估计误差协方差与各传感器传输概率的关系，在融合精度损失不大的前提下，得到一组次优的传感器传输概率，避免了高维矩阵的求逆计算和处理局部估计误差之间的交联，有效提高了实时性。结果表明，模型的不确定性越大，融合估计误差越大。因此，在实际中可通过减小建模的不确定性来提高融合估计精度。