基于双重优化的高速列车节能运行研究

2020-07-30杨宏阔

铁道运输与经济 2020年7期

陈昱，侯涛，杨宏阔

（兰州交通大学自动化与电气工程学院，甘肃兰州 730070)

0 引言

高速铁路具有速度快，运输能力大等特点，可以促进城乡协调发展，然而高速铁路列车的运行需要消耗大量能源。据调研，某铁路局集团公司1 a内列车牵引用电电费100 多亿元。因此，高速列车节能问题一直是近年来研究的热点问题[1]。

高速列车运行节能优化是在保证列车安全、准点的前提下，设计列车的运行曲线，得到运行消耗最少的能源方案。针对高速列车节能优化问题，国内外学者已经有了大量的研究。Kang[2]针对满足站点间距和行驶时间2 个约束条件的惰行点，提出了基于遗传算法的优化方法，并得到列车能量效率最优的节能运行曲线。王青元等[3]考虑列车再生制动，建立列车节能优化模型，并采用极大值原理求解，得到列车最优控制工况集。曹佳峰等[4]建立能耗模型，分析降低能耗的方法，将整个优化过程分为2 段：第1 段优化运行坡道，第2 段实行全面线路惰行优化。然而，这些研究在列车建模和节能控制策略上仍存在一些不足，有待进一步深入研究。

针对高速列车节能运行研究，先建立列车多质点模型，考虑列车运行中时间条件及停车的准确性，并充分利用坡道条件，通过遗传算法生成坡道速度序列，获得基础节能速度曲线，再利用遗传算法搜索工况转换点的位置，在运行过程中间阶段插入多个“牵引—惰行”工况，在满足时间条件的基础上，降低列车实际运行过程中产生的能耗，达到节能运行的目的。

1 高速列车能耗模型构建

1.1 列车动力学模型

列车动力学建模分为单质点模型和多质点模型2 种。其中单质点模型简单明了，容易计算，然而这种建模方式忽略了列车的长度及车厢之间的作用力，导致其附加阻力的计算有较大的误差，将列车在变坡点和变曲线点处速度视为跳变，从而使一些坡道变化频繁的线路计算的能耗值不精准[5]。而设计列车多质点模型，能够按每个车厢的长度和质量分别计算列车各节车厢在运行过程中所受的附加阻力，准确地模拟列车在经过变坡点和变曲线点处所受阻力的变化过程。针对坡道变化频繁的道路，多质点模型能使列车阻力计算精度显著提高，能耗计算更加精确。列车的多质点模型如图1 所示。

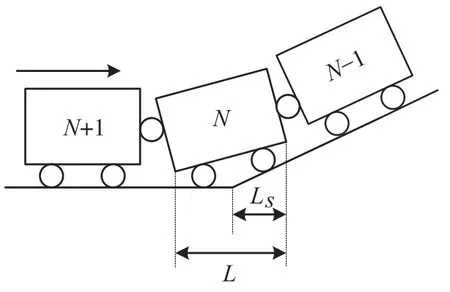
图1 列车的多质点模型Fig.1 Multi-particle train model

图1 中，L表示第N节车厢的长度；Ls表示第N节车厢越过变坡点的部分的长度。列车制动的过程十分复杂，可采用反向迭代的方法计算列车制动曲线，得到制动点。具体做法为：在停车点以固定的加速度反向迭代得出曲线，并与速度优化所得曲线相交于一点，即为制动点，从而推得制动点到停车点的制动距离。

1.2 列车运动学方程

列车在节能运行过程中，采用牵引、制动、惰行、巡航4 种工况[6]。在巡航工况下列车匀速运行，合力C= 0 N；惰行工况下，列车只受运行阻力W，则合力C= -W；制动工况下，列车所受的力为制动力B和运行阻力W，则合力C =-B-W。当C>0 时，列车为加速状态；C<0 时，列车为减速状态；C= 0 时，列车为匀速状态[7]。根据牛顿第二定律，列车的加速度与所受的合力成正比

式中：a表示列车的加速度，m/s2；M表示列车的质量，kg。

列车的动力学方程可表示为

式中：v表示列车运行速度，m/s；s表示列车运行距离，m；F表示动车组牵引力，N；B表示列车制动力，N；W0表示列车运行基本阻力，N；Wi表示坡道阻力，N；Wr表示曲线阻力，N；Wd表示隧道阻力，N。

1.3 列车能耗模型

具备再生制动功能的高速列车的能量分为输出和反馈两个流动方向。输出是在列车运行过程中提供牵引动力和克服运行阻力所消耗的电能。反馈则是靠制动时列车装有的再生制动设备将能量反馈到电网或车载储能设备。将输出和反馈能量分别计算，最后得到的能耗就是输出的能量与反馈能量的差值，计算公式为

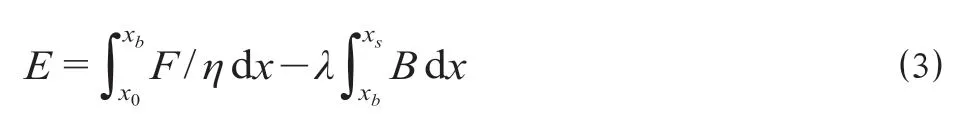
式中：x0为起始点；xb为列车的制动点；η为列车的牵引效率，与列车运行速度有关[8]；xs为运行终点；λ表示列车的制动效率，与列车运行速度有关[9]。

2 基于双重优化的高速列车节能策略

2.1 遗传算法寻优方案

坡道运行优化能耗模型和全线惰行优化能耗模型都属于非线性规划模型，且模型中涉及的高速列车运行时间、运行距离、加速度、能耗需通过微积分计算得到，模型求解难度较大。与精确算法寻找模型的收敛结果不同，采用遗传算法的编程实现虽然较为复杂，但通过高效地迭代进化可以找到逼近最优解的满意解。因此，设计遗传算法对所建能耗模型进行求解。具体步骤如下。

（1）种群初始化。初始化包括个体编码和产生初始种群。编码方式采用二进制编码，遗传算法的控制变量为列车运行线路子区间所对应的目标速度值。利用设计的编码规则，选取合适长度的染色体，形成初始种群。

（2）适应度函数与性能指标。对于算法进化过程中产生的每条染色体，首先通过解码得到相应子路段的目标速度，然后根据列车节能模型计算列车在速度序列运行下的能耗和时间，不满足限速和时间条件的无效序列被删除。性能指标评价函数为

式中：J表示性能指标评价函数；E表示列车在运行区间的能耗。

在公式 ⑷ 的基础上结合设置的调整系数得到公式 ⑸ 所示的适应度函数f

式中：A为设定的调整系数。

（3）遗传操作。遗传操作包括选择、交叉和变异。采用“轮盘赌”方法进行选择操作。“轮盘赌”方法的原理为个体适应度越高，被选中的概率就越大，根据公式 ⑷ 与公式 ⑸，得出个体x被选中的概率px为：

式中：fx表示个体x的适应度；fsum表示个体x所在子种群的总适应度；N表示个体x所在子种群的大小。

交叉操作采用单点交叉的方式。在二进制编码中，随机选择染色体中1 个点，以这个点为界限相互交换变量。两条染色体交叉的过程为

式中：R1、R2分别表示2 条父代染色体；、分别表示交叉操作后的2 条子代染色体。

采用单点变异的方式完成变异操作，以设定的小概率值随机改变种群中个体某些基因的值。

（4）通过以上操作获得新种群，代替之前的种群，迭代次数Gen=Gen+ 1。

（5）算法终止条件。在算法达到最大迭代次数或适应度值不再上升时停止循环，输出各个子路段目标速度序列，如果为达到终止条件，则返回步骤 ⑵。最大迭代次数的选取是根据实验得出的。进化次数过少，算法无法获得最优解；进化次数过多，算法的计算时间过长。

2.2 双重优化策略

目前研究通常将列车运行曲线进行1 次优化，且以全局优化为主[10-11]，在整个列车运行过程中没有充分利用线路的数据信息。在寻优策略上从2 个层面对高速列车进行节能优化操纵能够取得更好的效果。第1 重节能是将坡度相同的等斜率连续线路作为1 个子路段，利用遗传算法为各个子路段搜索目标速度，从而生成1 条满足时间、限速等约束条件的节能运行曲线。第2 重节能是根据第1 重优化得到的速度曲线，充分地利用惰行工况，再次优化中间运行阶段，达到进一步节能的目标。具体为通过提取列车运行中速度波动较小的中间段速度范围并小幅度增减，得到的速度范围即为列车理想运行速度范围。以列车准时到站、定点停车为前提，再次利用遗传算法搜索惰行点插入的位置，实行惰行模式下降低能耗，同时使工况的转换更加合理。第1 重节能优化流程图如图2 所示。

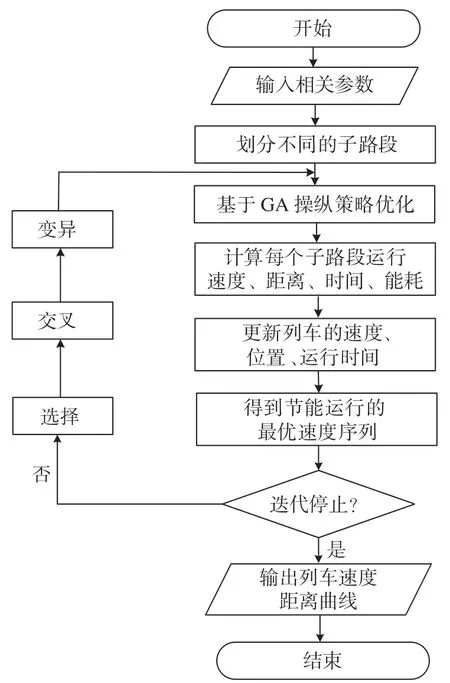
图2 第1 重节能优化流程图Fig.2 First energy saving optimization flow chart

以制动点为分界点研究列车节能运行曲线。假设制动点位于第n个子路段，将制动点前每个坡度相同的等斜率连续线路视为1 个子路段，则此线路区间集合为S= (s1，s2，…，sn-1，sn)，对应的子路段目标速度序列为V= (v1，v2，…，vn-1，vn)。设子路段限速为vilim，则每个子路段的目标速度需满足vi<。利用遗传算法搜索各个子路段的目标速度并生成1 条节能运行曲线，在列车根据该曲线运行时能够达到能耗最小的目的。第1 重节能优化运行示意图如图3 所示。

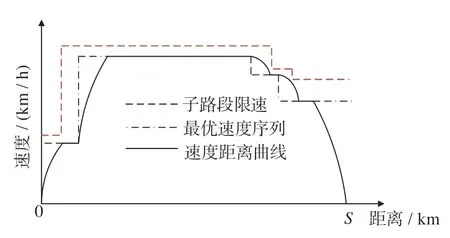
图3 第1 重节能优化运行示意图Fig.3 Schematic diagram of the first energy-saving optimization operation

第2 重优化的目标与1 重优化不同，遗传算法搜索目标由各个区间的速度变为“牵引—惰行”工况转换点的位置及速度，从而达到进一步节能的目的。

为了达到更好的节能效果，在第1 重优化的基础上，需要适当调整列车在中间“牵引—惰行”阶段允许的最大速度范围，扩大遗传算法的搜索范围，由于惰行是运行能耗最低的工况，因而在列车运行中间阶段插入多个惰行工况点。

第2 重优化针对的目标线路是第1 重优化后中间平稳运行阶段，启动和制动仍然采用第1 重优化的运行方式。遗传算法染色体编码仍然以二进制编码的方式，优化目标转变为列车运行中间速度平稳阶段所插入的“牵引—惰行”工况转换点位置，将一组工况转换点位置用具有n个基因的染色体Rx =(rx,1，rx,2，…，rx,n-1，rx,n)表示，按照列车运行距离递增的顺序随机生成。在遗传算法的步骤 ⑵ 中，针对生成的每一个染色体进行解码得到实数值，即对应工况转换点的实际位置Zx=(zx,1，zx,2，…，zx,n-1，zx,n)，根据公式 ⑶ 求解列车沿此工况转换点位置的运行能耗，同理，若不满足第2次优化节能模型中的时间、限速等约束条件，此组工况转换点无效，通过算法剔除并重新选择，其他步骤均与第1 重优化相同。第2 重节能优化运行示意图如图4 所示。

3 实例仿真

以合肥—蚌埠站间线路为研究实例。此线路全长117.7 km，运行时间为41 min，允许时间误差为30 s。车型为CRH3 型动车组。CRH3 型列车参数如表1 所示[12]。

基础节能速度曲线如图5 所示。由图5 知，经过第1 重优化后的速度曲线达到了准点运行与限速运行的要求。放大图具体解释了速度转换过程：首先，列车经过牵引保持恒定加速度加速，达到下一区间的目标速度，保持匀速运行；之后，采用惰行工况减速达到下一区间的目标速度并在列车到达下一区间前保持匀速运行。列车在整个运行过程中，采用了数个惰行工况，实现了基础节能。

根据能耗计算公式得出第1 重优化后的总能耗为2.241 3×1011J，运行时间为2 456 s。在基础速度范围内再次使用遗传算法得到数个工况转换点的位置，在此速度范围内插入数个“牵引—惰行”工况，实现对列车速度曲线的2 次优化。双重优化速度曲线如图6 所示。从图6 中可以看出，第2重优化加入了数个惰行工况，并且将基础速度进行了上下限小范围调整。计算得出列车的运行总能耗为2.037 2×1011J，运行时间为2 468 s，满足要求。未经任何优化的曲线能耗为2.411 8×1011J，运行时间为2 473 s。

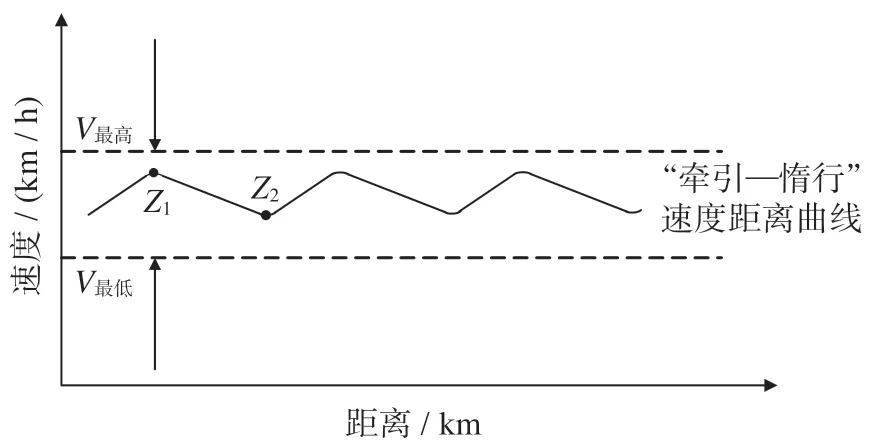
图4 第2 重节能优化运行示意图Fig.4 Schematic diagram of the second energy-saving optimization operation

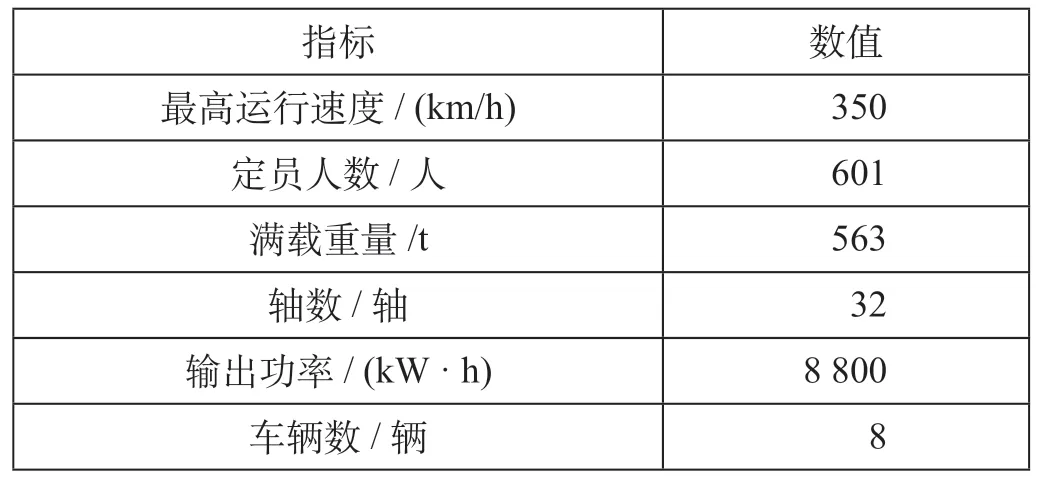
表1 CRH3 型列车参数Tab.1 Parameters of CRH3

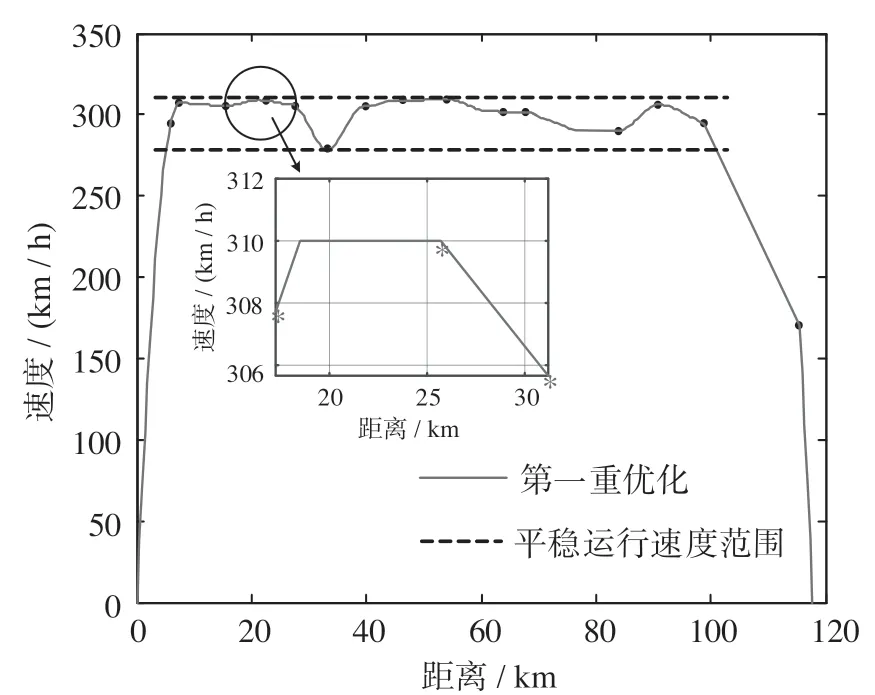
图5 基础节能速度曲线Fig.5 Basic energy saving speed curve

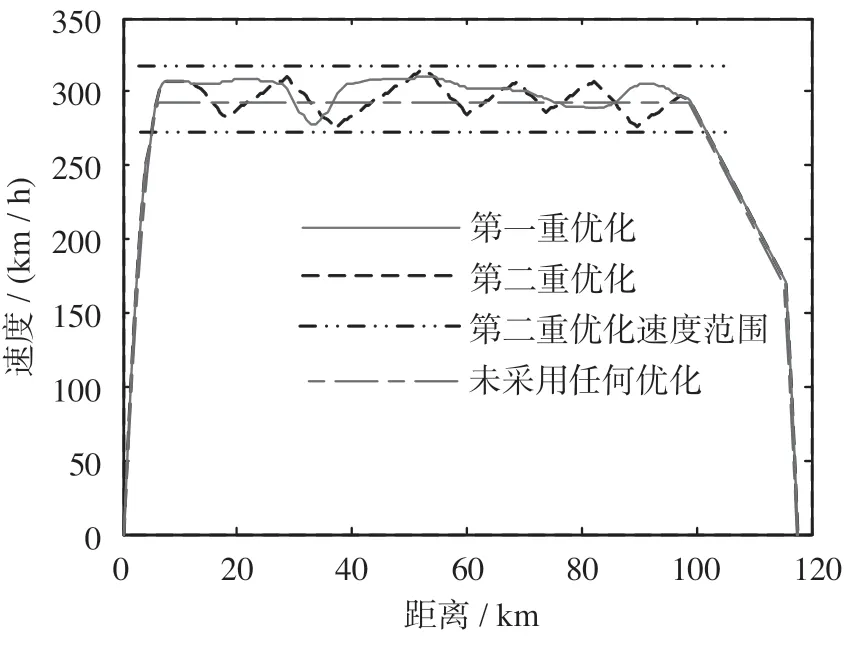
图6 双重优化速度曲线Fig.6 Double optimized speed curve

不同优化程度曲线能耗对比分析如表2 所示。

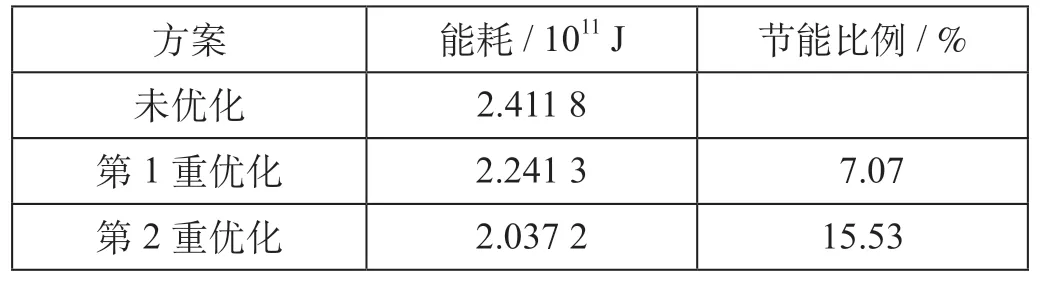
表2 不同优化程度曲线能耗对比分析Tab.2 Energy consumption analysis with different speed curves

由图6 与表2 知，不采用任何节能优化策略与经过双重优化后的列车平均速度基本相同，都能准点运行。然而，经过双重优化后的策略，由于采用了更多的惰行工况，大大降低了列车运行过程中的能耗。所提出的操纵策略能在合理的速度范围内充分利用坡度及牵引—惰行工况进行2 次优化，与未进行优化的方案比，总体节能15.53%，证明了所提出的控制策略的有效性。