基于实测白榆蒸腾速率校正计算液流速率的Granier原始公式*

马玉洁 李春友 武鹏飞 尹昌君 马长明

(1. 河北农业大学林学院 保定 071000； 2. 河北省林木种质资源和森林保护重点实验室 保定 071000； 3. 中国林业科学研究院林业研究所 北京 100091)

利用植物液流速率可计算树木蒸腾耗水量和掌握其需水规律。从20世纪60年代开始，研究者提出了多种树木蒸腾测定方法(刘奉觉等， 1997； 魏天兴等， 1999； 张劲松等， 2001)，例如快速称重法(Francnoetal., 1965)、整树容器称重法(Knight, 1981)、同位素示踪法(Dye, 1992)、染色法(Edwardsetal., 1984; Waring, 1979)、大型蒸渗仪法(Edwards, 1986; Heemyong, 2001)等。目前，以热技术为基础的方法应用最广泛(Hoelscheretal., 2018; Mineretal., 2017; Nadezhdina, 2018; 顾大形等， 2019； 李焕波等， 2008； 孙迪等， 2010； 徐利岗等， 2016)，其中热扩散式探针法(TDP)因其具有操作简单、价格低廉、使用周期长等优点而成为树干液流测定的主要方法。热扩散探针法是Granier(1985)通过对花旗松(Pseudotsugamenziesii)、欧洲黑松(Pinusnigra)和英国栎(Quercuspedunculata)3个树种进行有效拟合得出了TDP原始公式(Granier, 1985)，并认为该计算公式也适用于其他树种，但近年来部分学者对其准确程度提出质疑，如Bush(2010)等对4个环孔材树种沙枣(Elaeagnusangustifolia)、美国皂荚(Gleditsiatriacanthos)、深裂叶栎(Quercusgambelii)、国槐(Sophorajaponica)的校正公式与 Granier 原始公式相比存在较大差异，Taneda(2008)等也校正了基于深裂叶栎和北美大齿槭(Acergrandi-dentatum)的树干液流计算公式， 对山毛榉(Fagusgrandifolia)(Steppeetal., 2010)和多枝柽柳(Tamarixramosissima)(Hultineetal., 2010)的校正则进一步表明，Granier原始公式计算的液流速率比称重法测定值低估最高达46%。

白榆(Ulmuspumila)是典型的环孔材树种，其材质均匀，具有适应性强、保水力强、导水率较好等优良特性，是我国应用最广泛和重要的乡土造林树种之一。目前，Granier原始公式在榆树树干液流中的应用适应性未见报道，是否存在误差尚未验证。鉴于此，本试验以白榆为研究材料，通过评估Granier原始公式计算的液流速率与称重法得到的蒸腾速率之间的差异性，并构建热扩散式探针法测定的温差系数(K)与整树容器称重法获取的蒸腾速率之间关系，为提高白榆蒸腾耗水估计精度提供科学依据。

1 材料与方法

1.1 试验地概况 试验地位于河北省保定市河北农业大学野外试验站(38°81′ N，115°41′ E)，该地区属暖温带大陆性季风气候，四季分明，年均气温为13.4 ℃，年均日照时数为2 511 h； 年均降水量约498.9 mm，降水多集中在夏季，7月份降水量最大； 年均蒸散量约为1 430 mm，年均风速为1.8 m·s-1。

1.2 试验方法 1)大型容器栽植试验 2018年3月25日，从附近苗圃选择生长健壮、树冠圆满的白榆6棵，栽植于大型容器中(直径100 cm、高90 cm)，栽植前在容器底部垫土30 cm，将树木栽植到容器中央，容器周围裹隔热膜，栽后进行正常水分管理。在蒸腾量较大的7月份，选择生长状态良好、长势基本一致的3棵白榆进行试验(表1)。

表1 3株白榆样木的基本生长特征Tab.1 Basic characteristics of sample trees of Ulmus pumila

2) 树干液流速率测定 利用北京雨根科技有限公司生产的热扩散式茎流计(AV-3665R)进行测定，测定计算理论原理同原Granier型(何春霞等， 2018)。探针规格为20 mm，数据采集器型号为RR-1016，稳压器电压调至2 V，采用12 V蓄电池供电。监测上、下2根探针的温度差，通过Granier公式计算液流速率。

2018年7月1日，安装茎流计。首先在树木的南侧安装探针，在探针安装处刮去粗糙树皮，注意不要伤害形成层，然后采用特定规格的钻头，依据仪器自带钻模沿树干纵向垂直钻取直径为2 mm的孔洞。加热探针在上、下2个探针交替插入树木边材； 探针插好后，用1/4泡沫球将探针固定，外面包裹绝缘、防辐射材料，最后用胶带密封，减少辐射、雨水对探针温度的影响。将TDP反馈线与数据采集器连接，用以自动采集和记录数据，间隔期为60 s。基于Granier原理计算液流速率的原始公式(Granier, 1985)如下：

Fd=0.011 9×K1.231,

Fs=Fd×As，

K=(ΔTmax-ΔT)/ΔT。

式中：Fd为液流速率(sap flux density，cm3·cm-2s-1)；Fs为液流量(sap flow，cm3·s-1)； ΔTmax为无液流时的探针最大温差值(℃)； ΔT为某一测定时刻的温差值(℃)；As为样树的边材面积(cm2)。

在野外测定结束后的11月初，用生长锥分别在3棵白榆树干测定部位的4个方向钻取树芯，通过染色法，利用游标卡尺，测量边材宽度，计算白榆的边材面积。

3) 树木蒸腾速率测定 用整树容器称重法。选择天气晴朗、无风的连续5天(7月2—6日)，利用大量程天平(型号XK3190-A6、量程1 000 kg、精度20 g)对桶栽大树进行整树称量，称量时间为每天的6:00—19:00，时间间隔1 h。称量前日进行充足灌水，并用塑料薄膜将土壤表面密封。为尽量减少天平称量误差，采用手摇式叉车将容器放到天平上标记过的位置，并在搭建了阳光板式控制室进行称量。通过2次称量间隔值计算蒸腾量，蒸腾量除以边材面积为实测的蒸腾速率基准值。为提高与液流速率的可比性，蒸腾速率与液流速率的单位统一为cm3·cm-2s-1。

1.3 数据统计与分析 使用Microsoft Excel 2016对试验数据进行数据整理，以称重法测定的蒸腾速率为因变量，热扩散式探针法测定的温差系数K为自变量，通过SPSS22.0的曲线估计对7月2—4日的数据进行拟合，得到Granier校正公式。利用7月5—6日的数据，对Granier校正公式进行验证。液流速率指Granier原始公式或校正公式的计算值，蒸腾速率指整树容器称重法的实测值； 差异率是蒸腾速率与液流速率的差对蒸腾速率的比值。利用Origin9.5制图。

2 结果与分析

2.1 称重法实测蒸腾速率与Granier原始公式计算液流速率的变化 热扩散技术测定的液流速率和称重法测定的蒸腾速率的变化比较如图1。在连续3天测定中，蒸腾速率与液流速率均有明显日变化特征，两者的峰值都出现在13:00—14:00之间，二者的日变化趋势基本一致，但蒸腾速率始终大于Granier原始公式计算的液流速率，说明Granier原始公式的计算值严重低估，差异率一直在80%以上(图2)。因此，很有必要校正Granier原始公式。

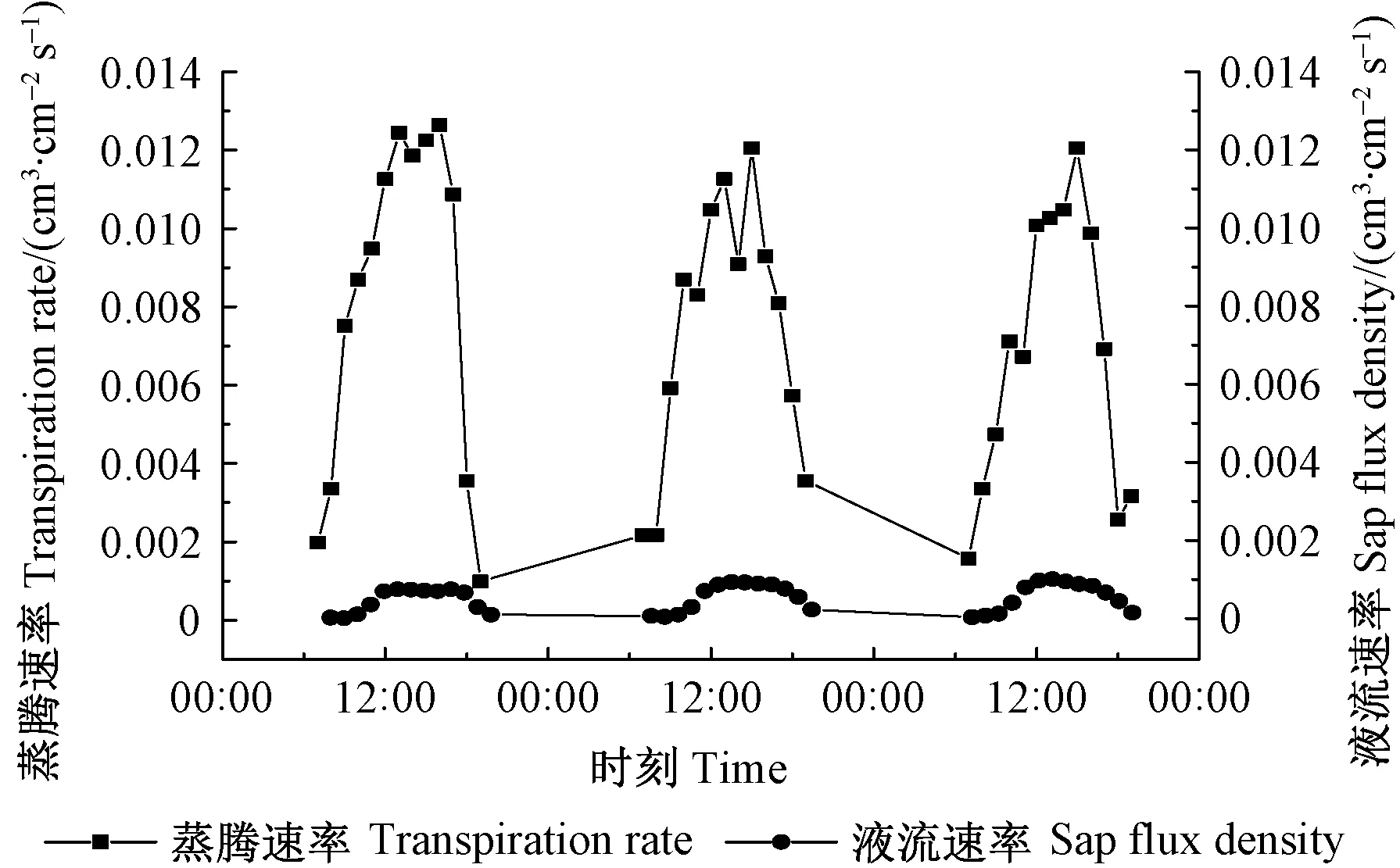
图1 白榆蒸腾速率和液流速率的日变化Fig.1 Diurnal variation of transpiration rate and sap flow rate of U. pumila

图2 基于原始公式的差异率变化特征Fig.2 Variation characteristics of difference rate based on original formula

2.2 Granier原始公式的校正 由于Granier原始公式不能较好地反映白榆的真实液流速率，对Granier原始公式进行了校正，拟合得到适合白榆的公式：Fd=0.059 6K0.916 4(R2=0.704 9)，可较好反映蒸腾速率随K值的变化关系(图3)。校正后的2个参数与Granier原始公式的参数差异明显，其中校正公式中的参数a=0.059 6比Granier原始公式的参数(a=0.011 9)大5倍，而参数b=0.916 4明显低于Granier原始公式中的参数(b=1.231)。

图3 称重法测量的蒸腾速率随参数K的变化Fig.3 Variation of transpiration rate measured by weighing method with parameter K

2.3 Granier校正公式的验证 利用2天校正期测定数据和Granier原始公式及校正公式计算的白榆液流速率与称重法测定的蒸腾速率的差异比较(图4)，发现三者的日变化规律基本一致，均随时间增加逐渐增大，在14:00—15:00达到最大值，随后又逐渐降低。虽然Granier校正公式计算的液流速率与真实的蒸腾速率曲线并不完全吻合，但远优于Granier原始公式，且二者之间不存在显著性差异。

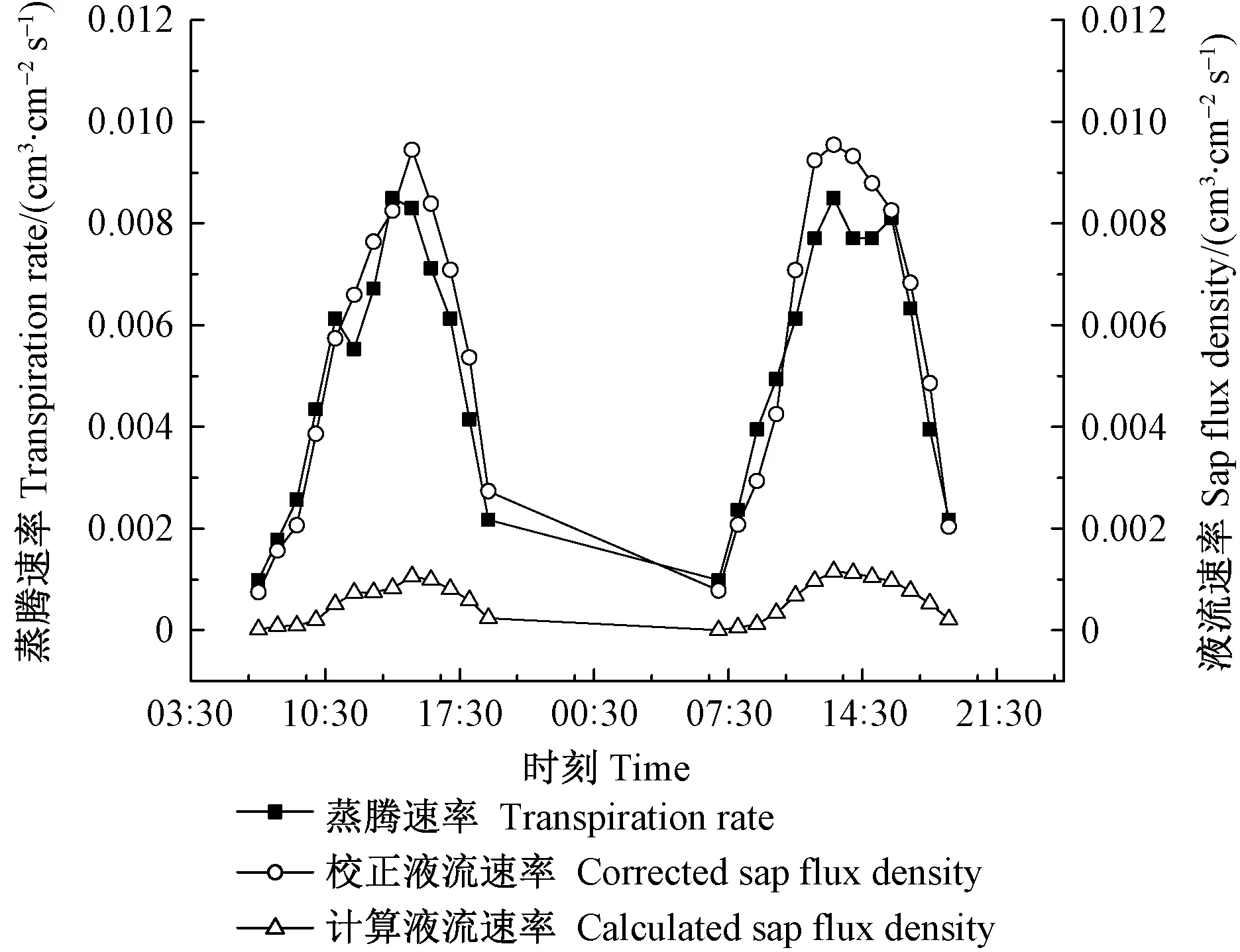
图4 白榆蒸腾速率和液流速率日变化特征Fig.4 Diurnal variation of transpiration rate and sap flow rate of U. pumila

利用校正公式计算的白榆液流速率相对称重的蒸腾速率有了很大改善(图5)，其差异率基本稳定在-30%～30%之间。虽然校正公式计算的液流速率比实测蒸腾速率仍有不同程度的高估或低估，但已经比较接近于真实蒸腾速率。

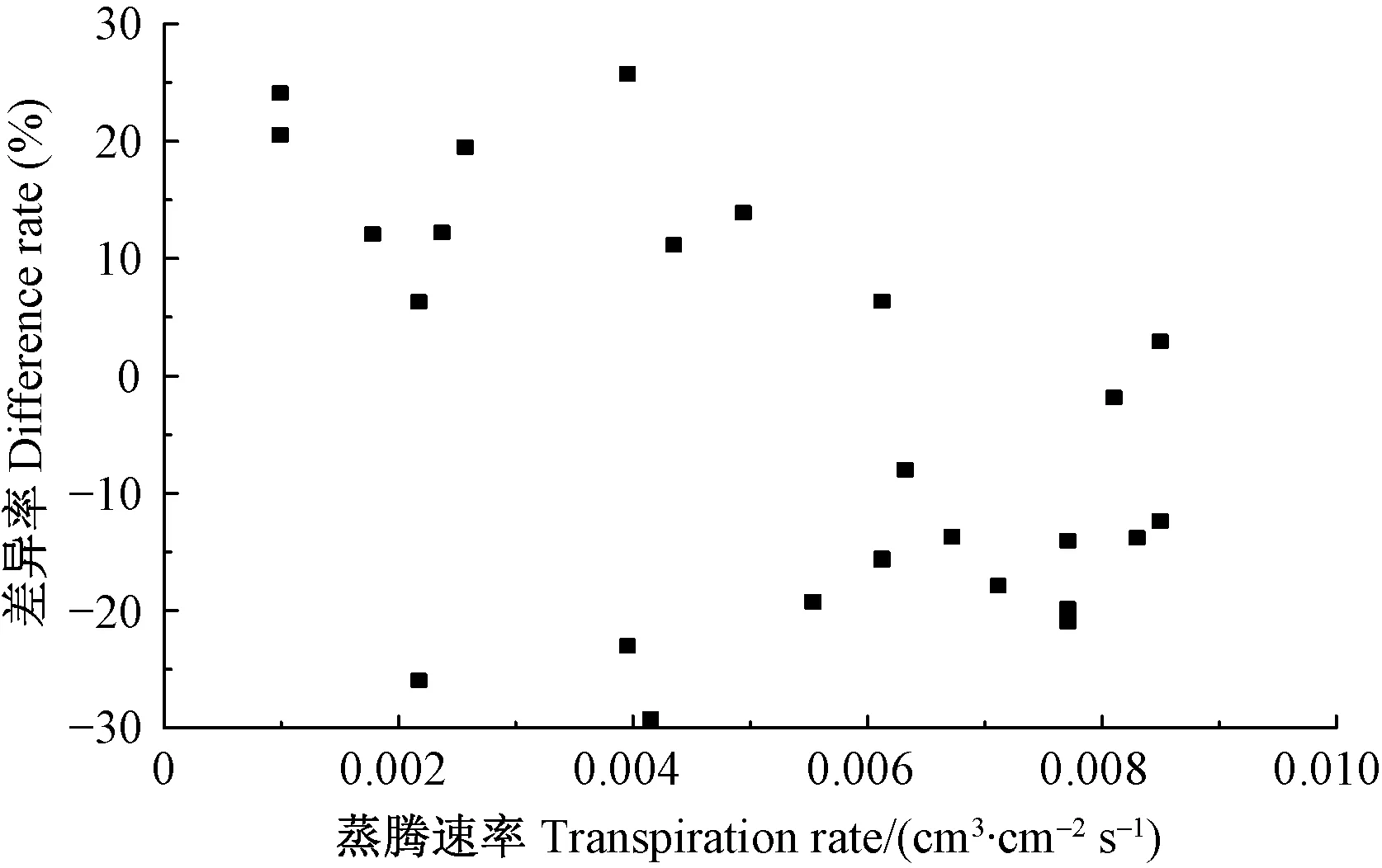
图5 基于校正公式的差异率变化特征Fig.5 Variation characteritics of difference rate based on correction formula

将实测蒸腾速率与校正公式和原始公式计算的液流速率相比(图6)，校正公式计算的液流速率接近1∶1直线，而原始公式计算的液流速率明显低于1∶1直线。可见Granier原始公式计算的液流速率明显低估了真实值，说明应用校正的Granier公式能提高白榆蒸腾速率的计算精度。

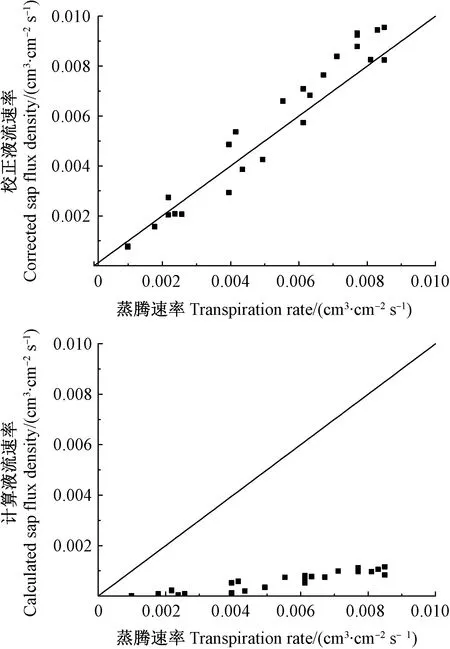
图6 验证校正的和原始的Granier公式Fig.6 Verifying the corrected and original Granier formula

利用实测数据和校正公式计算的日液流量与称重测定日蒸腾量的对比表明，二者在日尺度上无显著差异(图7)，与实测蒸腾量相比，误差分别为8.48%、8.37%、7.30%、-7.28%、-7.18%； 而原始公式计算的液流量比实测日蒸腾量分别低93.51%、92.25%、91.22%、89.23%、88.77%。以上结果说明，Granier校正公式比原始公式适于估计白榆日蒸腾量。

图7 白榆液流量在不同计算方法下的差异Fig.7 Difference of U. pumila sap flow rate under different calculation methods

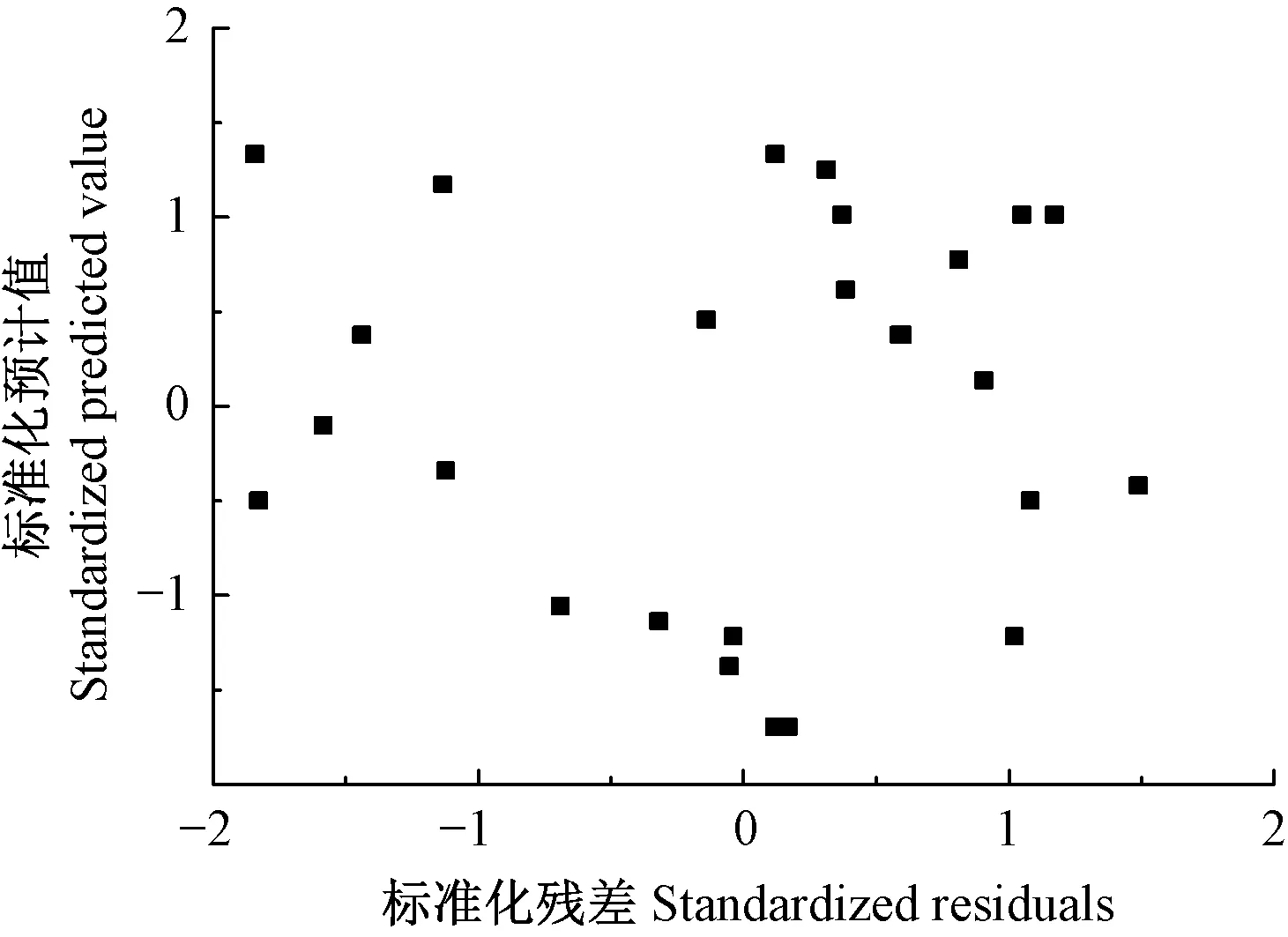
图8 残差示意Fig.8 Schematic diagram of the residual

3 讨论

热扩散式探针法(TDP)广泛应用于树木液流测定中，但只有少数人对Granier公式提出疑问，如Zhang(2017)等在利用TDP测定粉单竹(Bambusachungii)耗水准确性的研究中指出，Granier公式计算的液流速率较真实值低估约36%； Sun等(2012)比较了热扩散技术应用在环孔材树种美洲黑杨(Populusdeltoides)、针叶树火炬松(Pinustaeda)时的准确性，发现Granier原始公式计算的液流速率较实测值分别低估34%、高估55%； 而Fuchs等(2017)在对欧洲水青冈(Fagussylvatica)、心叶椴(Tiliacordata)、欧亚槭(Acerpseudoplatanus)这3个树种的研究中发现，使用Granier原始公式的液流速率计算值时，所有类型的TDP探针测定情况下都比真实液流速率低估23%～45%，并且误差随液流速率增大而升高。本研究以白榆为对象的验证表明，Granier原始公式计算的液流速率较真实蒸腾速率低估严重，其差异率在80%以上，因此，为了确保测量准确性，必须对每个树种的Granier原始公式进行校正(Smith， 1996)。

目前，绝大多数研究采用断面浸注法对Granier 原始公式进行验证和校正(刘庆新等， 2013),但该方法采用的材料为离体茎干，极易产生栓塞，会导致结果偏差，并且在校正试验前对离体茎干栓塞进行冲洗与否对液流速率计算有很大影响(Tanedaetal., 2008; Herbstetal., 2007)，可见该方法尽管实现测定值与探针记录值有效同步，但其本身误差还需进一步考虑。浸泡式整树容器法(Sunetal., 2012)虽然操作简便、计量较为精准，被认为是测量整株植物蒸腾耗水量最准确的经典方法(赵平等， 2012; Steppeetal., 2010; McCullohetal., 2007)，但对风引起的震动反应强烈，将树干从根际截断，仅采取树体地面以上部分来观测蒸腾作用，与自然生长环境脱离，而且观测总是处于水分供给的最优状态，叶片水势与气孔导度也会受到影响，因此该方法不能代表自然生长状态下的树木蒸腾量，且离体的树体也不能进行长时间连续试验。整树称重法使用的是栽植的活体树木，尽量模拟正常的生长环境，可以准确地表达出每小时的蒸腾量，与浸泡式整树容器法不同的是树木自然生长环境基本没有改变，可以长时间连续测定。整树称重法观测植物蒸腾作用既直接又快速，同时保证树木在水分充足条件下生长，避免胁迫对树体本身的影响，因此整树称重法测定的蒸腾速率较为准确。但整树容器称重法测定的是整株树木的蒸腾速率，传感器对液流速率变化的记录相对树冠蒸腾而言不是瞬时的，与树干液流之间存在时滞，在拟合方程时应根据时滞差进行数据错位。

不同树种校正结果具有较大差异。环孔材树种校正公式的系数与原始公式差异较大，如 Bush(2010)等对沙枣、美国皂荚、深裂叶栎和国槐校正Granier公式后得到的系数a分别为0.93、3.07、5.81、1.19，与Granier原始公式的a=0.011 9相差较大。散孔材树种的校正公式和Granier原始公式差异较小，如北美枫香(Liquidambarstyraciflua)和美洲黑杨校正公式的系数a分别是0.0124、0.0121，二者与Granier原始公式的系数a=0.011 9相差不大； 而校正系数b分别为1.151和1.141，略小于Granier原始公式的b=1.231(Sunetal., 2012)。这可能与树种的解剖、叶脉分布等结构性状差异有关。环孔材树种的边材导热率变化敏感(Wullschlegeretal., 2011)，且液流速率随边材深度的变化会有不同结果，并且因环孔材树种的边材厚度较小，在探针长度大于边材厚度的情况下，部分探针会插入心材，导致测定的液流速率被严重低估。 因此，不同树种类型的误差分析要结合木材材性特征。

植物的生物学结构决定树干液流的潜力，而土壤水分条件会影响树干液流的高低，土壤干旱胁迫会影响水分的吸收与传输，导致树干液流对气象因子的响应敏感性降低，同时降低蒸腾量和液流量，Kanalas等(2010)和Darby等(2016)的研究都证实了这一点。环境因子会影响树干液流的瞬间变动，其中土壤温度对液流速率在生长季并无影响，但在早春时二者相关性较强； 气温对树干液流的启动、停止、液流强度都影响更大。 本文研究条件是水分充足、温度适宜，未能考虑干旱胁迫(以及盐碱胁迫、温度胁迫等)对蒸腾速率与K值的关系的影响。因此，在未来的相关研究中，建议选择多种水分条件、气象因子条件下进行Granier公式校正，所取得的效果将更具有通用性。

4 结论

对于环孔材树种白榆，通过热扩散Granier原始公式计算的树干液流速率比整树称量测定的蒸腾速率偏低80%以上，存在严重低估，必须进行校正。校正后的Granier计算公式为：Fd=0.059 6K0.916 4，其计算值与称量实测蒸腾值基本一致。因此，白榆蒸腾速率需应用校正过的Granier公式来准确计算。