离网型风力发电系统中电励磁同步发电机的MATLAB 仿真设计
2020-07-29胡翼
胡 翼
(福建水利电力职业技术学院,福建永安366000)
伴随着全球“低能耗、低污染”的低碳经济发展,各国经济结构也发生了巨大的变化,全球进入了能源低碳转型期。大力发展清洁环保能源来逐渐减少对化石能源的依赖,是人类生存和发展面临的巨大挑战。我国作为世界能源生产大国,倡导绿色、低碳、循环、可持续的生产生活方式,通过能源供给结构优化,供电质量的提升,从一煤独大向清洁绿色转型,提高能源安全。风能作为清洁的可再生能源,一直备受关注。风力发电是目前能够具备大规模商业开发价值以及技术较为成熟的新能源之一。[1]我国的风能资源分布广泛,丰富的风能资源与水能资源季节分布恰好互补,大规模发展风力发电可以在一定程度上弥补我国水电冬春两季枯水期发电电力和电量之不足,[2]将其充分合理利用,有利于实现碳减排的目标。
本文以某学院离网型风力发电景观设计为原型,通过建立电机的数学模型,分析直接转矩控制方法,并在MATLAB/Simulink 上搭建离网型电力发电系统进行仿真,以此来验证该系统具有良好的性能,同时也展示风力发电系统控制的全过程。
1 电机的数学模型
电励磁同步发电机(Electrically Excited Synchronous Generator,EESG)的转子由直流励磁绕组构成,通过调节励磁电流,可改变磁场,从而实现变速运行时电机电压恒定,而且该电机无永磁材料,无失磁的风险,其价格也不受稀土价格波动的影响,生产投入成本低。但该电机需要空间来安放转子励磁绕组,体积较大。[3]而且电励磁的电流发热会引起一定的能量损耗。综合考虑本文选用电励磁同步发电机。
为了简化分析,本文对电励磁同步发电机的数学模型做以下几点理想化的假设:定子三相绕组完全对称,并且仅分析在绕组中产生的磁动势的基波分量;电励磁同步发电机的参数保持不变;磁路不饱和;电励磁同步发电机的定子铁心与转子铁心的磁阻均为零,即忽略定子与转子铁心的磁压降;忽略电励磁同步发电机的阻尼绕组,即仅考虑无阻尼绕组的情况;电励磁同步发电机运行时正方向采用发电机惯例。
电励磁同步发电机的矢量坐标如图1 所示。A、B、C 为三相定子绕组轴线位置。d 轴为转子N 极磁极方向,其与A 轴之间的夹角为转子旋转角θ,q 轴与d 轴垂直。
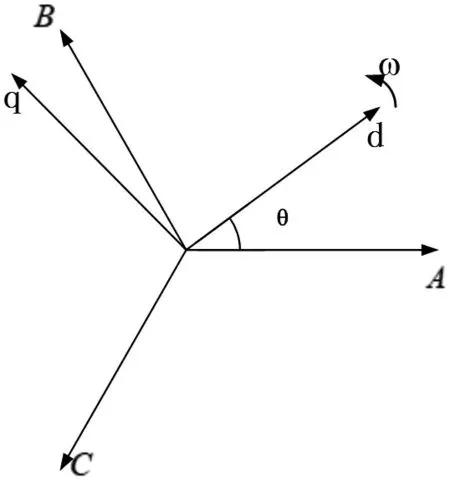
图1 电励磁同步发电机的矢量坐标图
其定子电压方程为:
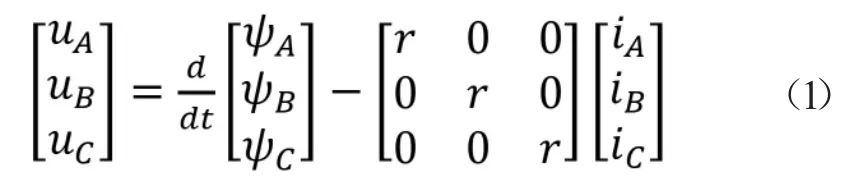
其中,uA、uB、uC分别为定子A、B、C 三相电压,iA、iB、iC分别为定子A、B、C 三相电流,ψA、ψB、ψC分别为定子三相绕组交链的磁链,r 为定子三相绕组电阻。
转子电压方程为:
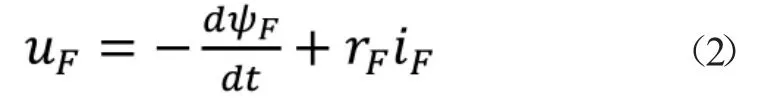
其中rF为转子励磁绕组电阻,iF为转子励磁电流,ψF为转子磁链。
为了简化电机数学模型,将进行Park 变换来消除定、转子磁链随θ 变化的问题,变换后定子等效的d、q 轴绕组就与转子绕组轴线重合并且相对静止。Park 变化前后,电机的数学模型在两个不同的坐标系中是完全等效的。
Park 变化后可以得到电励磁同步发电机定、转子电压方程、定转子磁链以及电磁转矩表达式为:

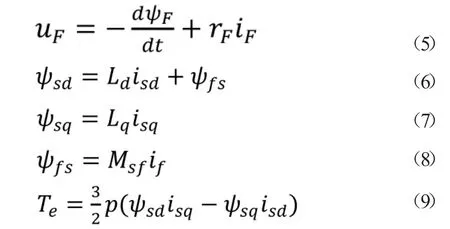
其中,ωr为转子旋转角速度,usd、usq分别为定子直轴电压、定子交轴电压,ψsd、ψsq分别为定子直、交轴磁链,isd、isq、if分别为定子直、交轴电流和转子电流,ψfs为转子磁链归算到d 轴上的分量,Msf为定转子绕组之间的互感,p 为电机极对数。
2 直接转矩控制系统分析
电励磁同步发电机定子绕组的电阻一般较小,其产生的铜损耗也可以忽略不计,则发电机的输出功率近似等于其电磁功率。而电磁功率与转矩的关系为:
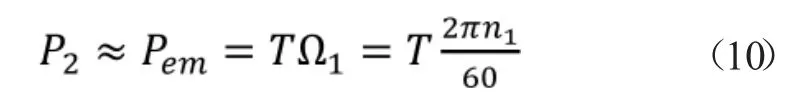
对于同步电机其转速为同步转速,在正常运行时,转速保持不变,电磁转矩与发电机的输出功率成正比。所以我们可以通过控制电磁转矩进而间接地控制发电机对外的功率。直接转矩控制系统(DTC)是直接控制电机的电磁转矩,控制结构简单,只需要选择最佳的电压空间矢量作用在电励磁同步发电机上,使电磁转矩误差与定子磁链误差减少,这样就实现了控制电机。
为了实现对发电机输出功率的快速控制,本文选择DTC 控制策略,将其定子磁链轨迹控制为圆形。直接转矩控制系统原理的结构图如图2 所示。从图中可以看出首先从电励磁同步发电机获得三相定子电压与电流,然后根据电机的定转子的数学模型,得到磁链与电磁转矩,将它们分别与给定值进行比较,得到磁链幅值偏差与电磁转矩偏差,接着根据定子磁链矢量的位置,确定扇区n。最后根据磁链幅值偏差、电磁转矩偏差、扇区n,选择合适的空间电压矢量,输入到逆变器中,完成对其的控制,使电机输出恒定电压。
直接转矩控制策略利用空间电压矢量直接控制,动态响应快。将其应用在电励磁同步发电机上,可以减少电励磁发电机转子参数对控制策略的影响,提高发电性能。
3 离网型电力发电系统的仿真模型
离网型风力发电系统的仿真模型主要包括:风力机的仿真模型、电励磁同步发电机的仿真模型、控制系统、逆变器的仿真模型、离线负载的仿真模型等。
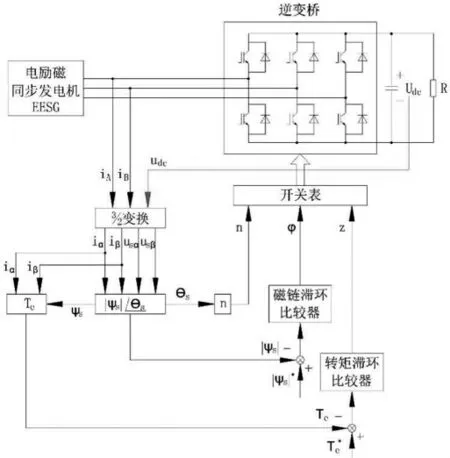
图2 直接转矩控制系统原理的结构图
3.1 风力机的仿真模型
目前一般采用直流电动机、异步电动机以及同步电动机对风力机进行数学建模,考虑到三种电机控制方法的优缺点,同时结合到自身实验条件,本文选择控制简单、更适合小功率系统的直流电动机来实现风力机的模拟,其风力机的仿真模型如图3 所示。

图3 直风力机的仿真模型图
3.2 电励磁同步发电机的仿真模型

图4 电励磁同步发电机的仿真模型图
电励磁同步发电机具有效率高,功率因数可调,过载能力强等特点[4],在电机的数学模型中,将电机的定子电压、定子电流、定子磁链进行dq 分解,定子电压直轴分量usd决定定子磁链幅值的增减,定子电压交轴分量usq决定电子磁链矢量旋转角速度。通过这样分解,形象地描绘出电磁转矩与转差频率,其电励磁同步发电机的仿真模型如图4 所示。
3.3 控制系统
本文采用直接转矩控制系统。在仿真模型中,采用滞环比较器对获得的定子磁链、电磁转矩与给定值进行比较,得到磁链幅值偏差、电磁转矩偏差,根据它们的偏差,决定定子磁链的增减和定子磁场的转向。最后结合定子磁链所处的扇区,选择合适的空间电压矢量,减少磁链幅值和电磁转矩的偏差。
为了直观地选择电压矢量,将定子磁链的圆形轨迹分为6 等分,6 个扇区。仿真模型中逆变器可以输出8 个空间电压矢量:2 个零矢量,6 个有效电压矢量。将这6 个非零的电压矢量作用在某一个时刻的定子磁链上,会使得该时刻定子磁链和位置发生相应的变化。下面以定子磁链在第一扇区为例进行说明(如图5 所示),当选择施加电压矢量u1时,可以使定子磁链矢量的幅值增加,同时朝顺时针方向旋转;当选择施加电压矢量u2时,可以使定子磁链矢量的幅值增加,同时朝逆时针方向旋转;当选择施加电压矢量u3时,可以使定子磁链矢量的幅值减少,同时朝逆时针方向旋转;当选择施加电压矢量u4时,可以使定子磁链矢量的幅值减少,同时朝逆时针方向旋转;当选择施加电压矢量u5时,可以使定子磁链矢量的幅值减少,同时朝顺时针方向旋转;当选择施加电压矢量u6时,可以使定子磁链矢量的幅值增加,同时朝顺时针方向旋转。在不同的扇区,施加不同的电压矢量,对其也会产生不同影响,在这里就不一一举例。
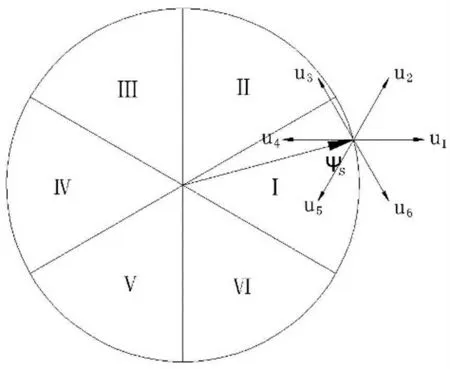
图5 定子磁链圆形轨迹扇区图
通过滞环比较器给出的误差,结合各个扇区电压矢量对电磁转矩和定子磁链幅值的作用效果,可以给出电励磁同步发电机直接转矩控制的最优开关矢量表。其控制算法模型如图6 所示。
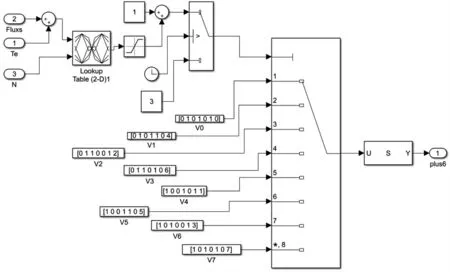
图6 直接转矩控制系统的控制算法模型图
3.4 逆变器的仿真模型
通过MATLAB/Simulink 软件自带的模型库,选择Universal Bridge。根据实际的逆变器的参数对其进行设置。其设置参数如图7 所示。

图7 Universal Bridge 仿真模型参数图
3.5 离网型风力发电系统直流侧负载的仿真模型
离网型风力发电系统将发出的电能消耗在景观灯上,故它的仿真模型采用电阻元件。其模型参数根据实际设置。
4 仿真实验结果分析
在仿真实验中,模拟环境风速选择10m/s(五级风力),电机的参数均选择额定运行情况下的参数。从仿真实验可以看出,在恒定的风速情况下,0-0.3s,系统起动并加速运行,系统稳定运行后,定子磁链的运动轨迹保持为圆形,如图8 所示,说明此时控制策略为直接转矩控制。直流母线电压在小幅度波动,如图9-b 所示,但都维持在负载的额定电压处,如图9-a所示。仿真的实验数据与实际运行情况相符,能较好地模拟实际离网型风力发电系统的运行情况。
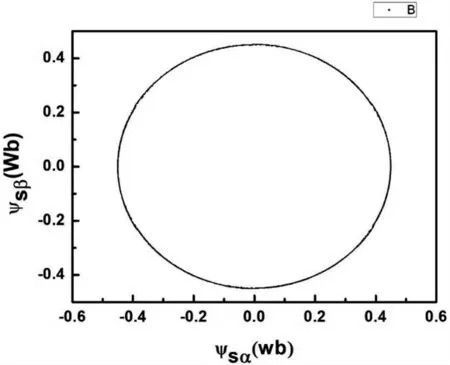
图8 定子磁链的运动轨迹图
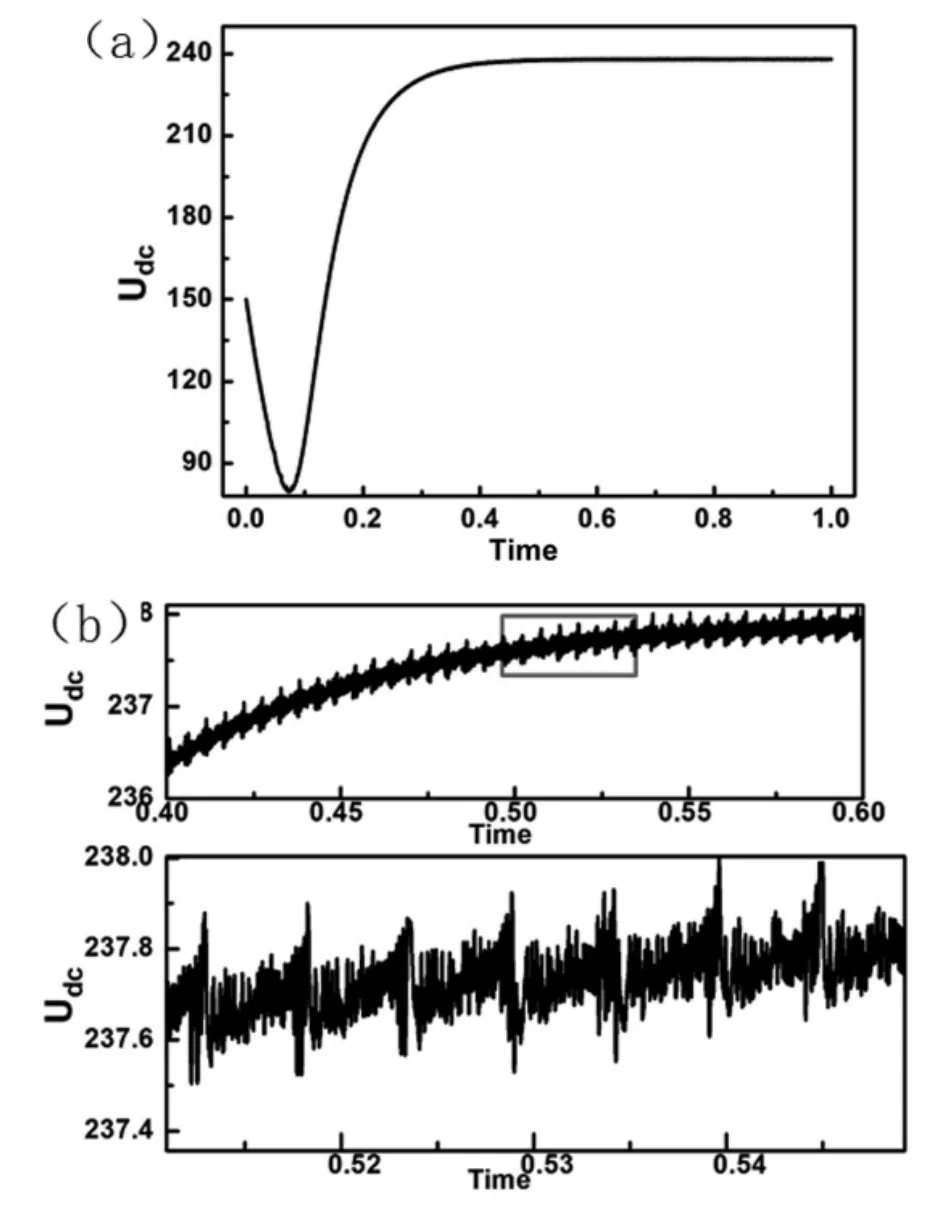
图9 直流母线电压图
5 结语
随着当前我国能源需求进一步增长,能源匮乏情况日益严重,风力发电技术的发展在当前成为人们关注的焦点。[5]本文以离网型风力发电景观设计为原型,在电励磁同步发电机数学模型的基础上,通过构建风力机的模型、电励磁同步发电机的模型、控制系统、离线负载的模型,实现MATLAB 仿真。仿真实验得到的仿真数据与离网型风力发电系统实际运行情况相符合。此仿真系统能较形象地展示风力发电的过程,对景观展示的演示有重要的意义,同时为进一步深入研究离网型风力发电系统提供有效的仿真平台。
