考虑公平的铁路应急物资调度优化研究

胡可昊，李 涛

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

0 引言

我国大规模灾害事件频发，给人民生命财产造成了巨大的威胁。当灾害发生后，需要立即由应急供应点向应急需求点运送大量物资，及时满足灾区物资需求，以降低灾区的受灾程度，稳定灾区秩序。但是在灾害发生后，应急供应点往往不能同时满足多个应急需求点的需求，会导致距离较远的应急需求点获得的资源量较少甚至没有的情况，因而在应急资源调度时，不仅需要考虑运送成本和运送距离，还需要确保多个受灾点的公平性。

应急资源调度具有不确定的特点，国内外学者引入不确定性理论来研究应急物资分配方案。Elisabeth等[1]提出了模糊集合论求解应急资源调度问题。Belmont 等[2]提出了基于模糊集合理论研究应急资源调度问题的方法。闫妍[3]围绕突发灾害情景演化，构建应急物资动态协同分配模型。于小兵[4]以成本最小，时间最短为优化模型，设计改进粒子群算法求解模型。樊友龙[5]在物资充足条件下建立多目标优化模型，并结合案例验证算法有效性。王海军等[6]考虑下一周期将优先配送供不应求的物资，通过对时间和成本的动态赋权，提高算法的柔性。李孟良[7]运用多目标优化等方法，研究在混合不确定条件下应急物流选址—路径问题、选址—配送问题和多式联运问题。黄露[8]以时间最短和满足率最大为优化目标，建立了物资分配模型，并运用鲁棒优化方法消除不确定需求对结果造成的影响。汤兆平等[9]运用模糊评价和熵权灰色关联理想法，对救援点进行排序，并设计TOPSIS 方法和限定参数区间搜索求解模型。

既有研究着重考虑如何在最短的时间内和运费最小的情况下把物资运送到应急需求点。但是，在灾害发生后，需要更好地照顾人们的心理情绪。有学者认为只考虑物资的运送时间最短忽略了灾区群众的情绪，在实际运送过程中会出现刻意追求时间最短和费用最小，导致各个应急需求点物资分配不均的现象；有学者考虑受灾群众的心理感受，提出将物资尽可能公平的分配给受灾群众。例如，李丹[10]用公平分配理论作为物资分配的基础，采用启发式多目标粒子群算法求解模型；Vitoriano 等[11]提出人道主义援救配送的多目标模型。目前，大多应急资源调度的研究都是在考虑模糊条件下资源如何更好更快地运送到应急需求点，仅有少量研究考虑了物资分配的公平性。因此，应充分考虑突发事件的特点，建立多供应点和多需求点的网络，在需求不确定的情况下，考虑物资分配的公平性，建立分配公平性最大和运输成本最低的铁路应急物资调度多目标优化模型，设计改进遗传算法进行求解。

1 铁路应急物资调度多目标优化模型

1.1 问题描述

应急供应点一般选择在靠近受灾地区且储存大量应急物资的中大型城市；应急需求点通常选择在受灾区附近且铁路线良好的车站，当应急物资运送到车站后，可由公路运输直接运送到受灾点。在突发事件发生后，受灾地政府向有关部门进行报告，申请救援。应急管理部门根据受灾地的受灾情况进行研讨，专家根据已有的经验和数据，结合受灾规模，大致确定受灾地的物资需求量。灾害发生后，由于应急需求点物资需求量急剧上升，附近应急供应点储存物资无法满足灾区需要，需要进行合理的资源调度。

在确定物资分配方案时，要考虑物资分配的公平性和运输成本最小。物资分配的公平性可以通过各个受灾点的物资满足程度比较进行确定。各个物资供应点的满足程度相差不大就说明该方案有较好的公平性。设有I个应急供应点，分别为G1，G2，…，GI；有J个应急需求点，分别为Z1，Z2，…，ZJ，应急供应点向应急需求点调度示意图如图1 所示。

图1 应急供应点向应急需求点调度示意图Fig.1 Diagram of scheduling material transportation from supply points to demand points

1.2 模型建立

对问题进行简化，作出以下假设：①应急供应点拥有各种物资的数量已知；②所有应急供应点拥有各种物资的总量不大于所有应急需求点所需该类物资的总量；③应急车辆行驶速度已知；④有足够的应急车辆来完成物资运送任务。

应急资源调度系统可以抽象为有I个应急供应点和J个应急需求点的配送网络系统。配送网络系统中有E种应急物资种类，分别为K1，K2，…，KE。以物资分配公平性最大和运输成本最低为目标，建立铁路应急物资调度多目标优化模型如下。

式中：f1为应急需求点资源满足率方差；pj为应急需求点j的物资满足率；p-为所有应急需求点的平均物资满足率；f2为应急物资调度的成本；Xije为0-1变量，表示是否有物资e从应急供应点i运送到应急供应点j，当有物资e从应急供应点i运送到应急供应点j时，取值为1，当没有物资e从应急供应点i运送到应急供应点j时，取值为0；Yije为非负变量，表示应急供应点i向应急需求点j运送物资e的数量；Ce为运送单位距离物资e的成本；dij为应急供应点i到应急需求点j的距离；gie为应急供应点i拥有物资e的数量；Q=je为应急需求点j需要物资e的模糊数量。

公式 ⑴ 为目标函数，表示最小化应急需求点资源满足率方差，即最大化物资分配的公平性；公式 ⑵为目标函数，表示最小化总物资分配费用；公式 ⑶为供应量约束，表示对于任意供给点i的任意一类物资e，由该供给点提供给所有应急需求点的物资e的总量不大于该供给点i中物资e的总库存；公式 ⑷ 为需求量约束，表示对于每一类物资，所有供给点的该类物资库存之和小于所有需求点的该类物资模糊需求之和(保证物资e在全局上是供大于求的)；公式 ⑸为单种物资需求量约束，表示对于任意应急需求点j的任意一类物资e，由所有供给点供给应急需求点j的物资e的总和小于该需求点对于该类物资的模糊需求；公式 ⑹用于计算应急需求点j的物资满足率；公式 ⑺ 用于计算应急需求点平均物资满足率。

多目标模型直接求解比较困难，因而将理想点法原理运用到多目标应急物资分配，把多目标的问题转化成单目标，经过处理后可得

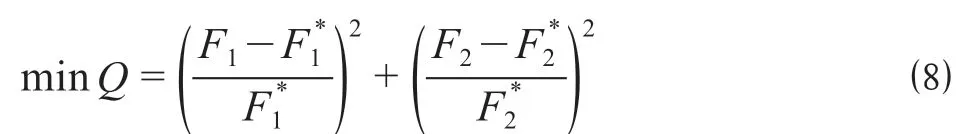
式中：Q为转化后的目标函数；F1，F2分别为模型的可行解代入公式 ⑴、公式 ⑵ 的取值；F1*，F2*分别为公平性和经济性的单目标优化的最优值。

1.3 模型求解

铁路应急物资调度多目标优化模型是多目标模糊规划模型，求解该模型首先要去模糊化，在此基础上，综合考虑2 个目标函数，采用改进遗传算法对模型进行求解。

1.3.1 去模糊化方法

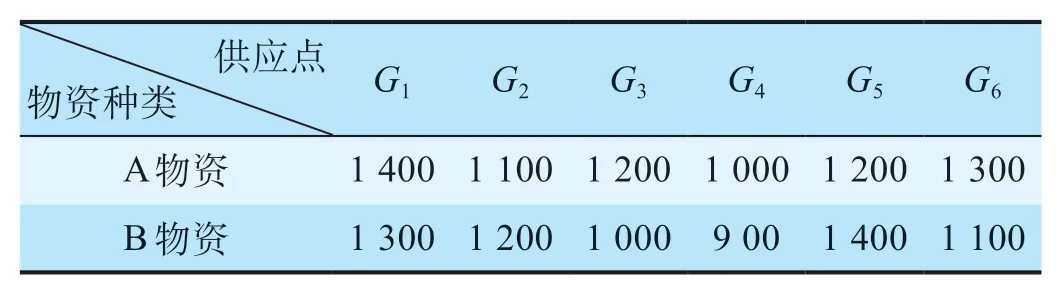
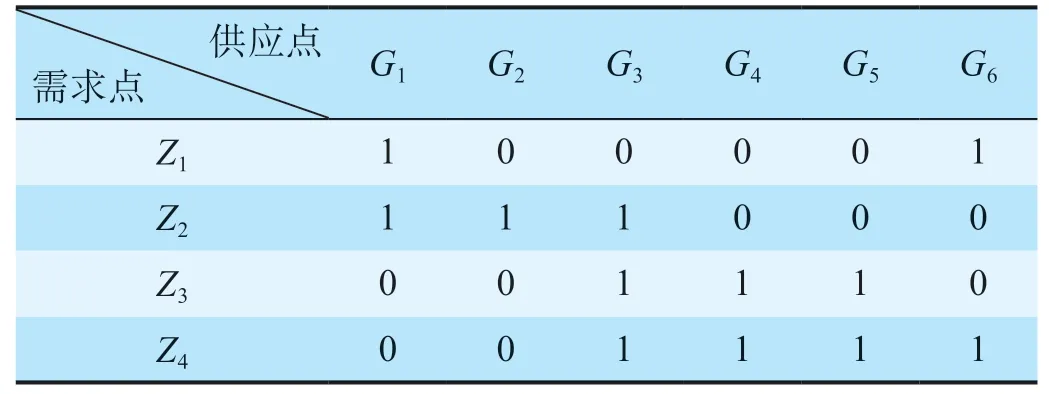
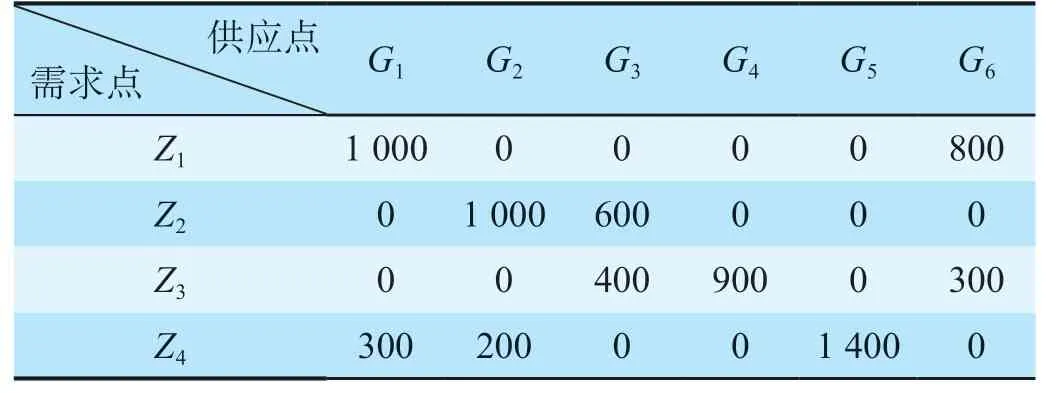
应急事件发生后，由于很难迅速得知灾区情况，就会给应急救援带来很大困难。从现实出发，在铁路应急物资调度多目标优化模型中引入了需求模糊值。在求解模型的时候将模糊值化为确定值，采用三角模糊数来描述应急需求点的模糊需求量，将模糊需求量记为A= (a，c，b)，其中a，b为模糊数的上下限，c为三角函数最有可能的取值，0

三角函数模糊隶属度函数FA(x)可以表述为

式中：x为三角模糊数隶属度函数自变量。

给决策者确定置信水平α后，采用平均权重法将三角模糊数转化为确定的数值，公式如下。

式中：A为采用平均权重法将三角模糊数转化为确定的数值；n1，n2，n3分别为三角模糊数下界，三角模糊数最有可能取值，三角模糊数上界的权重。

三角模糊数最有可能值是最重要的，因而分配的权重是最大的，其他三角模糊数的上、下界作为边界约束，分配的权重就相对较小。采用最可能值法确定权重，即n1=n3= 1/6，n2= 4/6 且α= 0.5，将模糊需求量转化为确定值，公式如下。

1.3.2 改进遗传算法

铁路应急物资调度多目标优化模型由应急需求点和应急供应点组成，结合实际的情况，模拟产生数据，采用改进遗传算法对铁路应急物资调度多目标优化模型进行求解，步骤如下。

（1）生成初始染色体。0-1 决策变量Xije采用二进制编码，非决策变量Yije采用实数编码，根据编码方式随机生成M个个体作为初始种群。

（2）计算适应度。将铁路应急物资调度多目标优化模型转化成单目标模型，计算种群个体的适应度。

（3）改进遗传算法。借鉴模拟退火算法中的拉伸方法改进遗传算法，不仅可以避免早熟问题，还可以避免陷入局部最优解。①将得到的适应度进行排序，取父代种群前1/4 的个体；②在父代种群中选取(1/2)K个个体，K为排除之前选中个体的种群规模；③将①中取出的个体与②中新子代进行模拟退火选择，然后将新得到的个体与原父代种群合并成一个种群，之后将各个染色体的适应度函数进行拉伸[12]，计算每个个体被选择概率，公式如下。

式中：P(d)为临时种群中每个个体被选择的概率；s(d)为适应度函数；Tv'为渐趋于0 的退火温度；T0为初始温度，v'= 1，2，…。

（4）交叉运算。采用单点交叉，在个体串中随机设定一个交叉点进行交叉，生成2 个新个体。

（5）变异运算。按照变异概率，采用禁忌变异算子进行变异操作。

（6）终止条件判断。当前迭代次数满足终止条件，输出适应度最好的解，得到应急物资调配方案。

2 算例分析

以受自然灾害影响某区域的Z1，Z2，Z3，Z44 处应急需求点，以及G1，G2，G3，G4，G5，G66 处应急供应点为例，采用铁路应急物资调度多目标优化模型对该区域应急物资进行合理分配，以验证铁路应急物资调度多目标优化模型的准确性和实用性。

2.1 基础数据

根据以往经验及现实情况给定需求模糊值。假设受灾点需要A，B 2 种物资，A 物资的单位运输成本C1为0.6 元/km，B 物资的单位运输成本C2为0.8 元/km。应急供应点到应急需求点的距离如表1 所示，应急需求点模糊需求物资数量如表2 所示，应急需求点需求物资数量如表3 所示，应急供应点物资供应数量如表4 所示。

表1 应急供应点到应急需求点的距离 kmTab.1 Distances from supply points to demand points

表2 应急需求点模糊需求物资数量Tab.2 Fuzzy quantity of required materials for demand points

表3 应急需求点需求物资数量Tab.3 Quantity of required materials for demand points

表4 应急供应点物资供应数量Tab.4 Quantity of materials at supply points

2.2 模型求解

结合实例，建立铁路应急物资调度多目标优化模型，并在Matlab 2016 a 上仿真求解。算法参数设置如下：种群大小N= 100，交叉概率pc= 0.8，变异概率pm= 0.05，迭代次数为1 000，T0初始温度取为100。供应点与需求点A 物资的0-1 状态变量值如表5所示，供应点与需求点B 物资的0-1 状态变量值如表6 所示，供应点提供给需求点A 物资的数量如表7所示，供应点提供给需求点B 物资的数量如表8 所示。经计算，应急需求点资源满足程度为0.029，应急物资调度的成本为1 500 340 元。

此外，采用传统遗传算法对该算例进行求解[13]，应急需求点资源满足程度为0.031 9，应急物资调度的成本为1 575 360 元。与传统遗传算法相比，改进遗传算法的应急需求点资源满足程度的方差减小了10%，成本减少了5%。由以上的结果可知，改进遗传算法具有更快的收敛速度和更优的求解性能。

Z2由于距离供应点较远，突发事件发生之初，供应点无法同时满足所有需求点，因而距离较远的Z2分到的资源应该最少，但是应急救援不应只考虑成本而不考虑实际情况，为距离较远的需求点提供救援虽然会增加成本但也是必需的。运用铁路应急物资调度多目标优化模型得到的调度方案可以使公平性趋近最大化，并且让调度总成本降到最小。

表5 供应点与需求点A 物资的0-1 状态变量值Tab.5 State variable values (from 0 to 1) of item a at supply points and demand points

表6 供应点与需求点B 物资的0-1 状态变量值Tab.6 State variable values (from 0 to 1) of item b at supply points and demand points

表7 供应点提供给需求点A 物资的数量Tab.7 Quantity of item a allocated by supply points to demand points

表8 供应点提供给需求点B 物资的数量Tab.8 Quantity of item b allocated by supply points to demand points

3 结束语

在突发事件发生后，铁路应急救援是降低突发事件人员伤亡和财产损失的有效手段，因而在第一时间制定应急资源调度方案具有非常重要的意义。铁路应急物资调度多目标优化模型针对多需求点、多供应点、多资源的不确定铁路应急资源调度问题，充分考虑调度公平性，从实际出发解决了多需求点、多供应点、多物资的应急物资调度问题，符合实际，结果合理，证明了模型与算法的有效性。该模型能够在铁路突发事件发生之初、总资源量不足时，有效避免距离较远的受灾点获得的资源量较少甚至不能获得资源的情况，为大规模应急物资调度问题提供有效依据。