一类3-正则图完美对集的计数

唐 保 祥， 任 韩

( 1.天水师范学院 数学与统计学院, 甘肃 天水 741001；2.华东师范大学 数学系, 上海 200062 )

0 引 言

图的完美对集计数理论的研究成果已经在计算机科学、物理学和化学等多个领域有广泛的应用．例如，DNA计算自组装模型的算法理论，计算机积和式二分图的完美对集表示，化学中共轭分子图Kekulé结构的完美对集表示，此外完美对集数还是估计共振能量和π-电子能量的重要指标．因此，研究图的完美对集计数理论有重要的理论价值和现实意义[1-3]．但是，此问题已经被证实是NP-难问题．分类嵌套递推的方法是求解许多类图完美对集数非常有效的方法[4-8]．本文构造一类新的3-正则图2-3-nC6，用分类嵌套递推的方法求出图2-3-nC6中不同完美对集的计数公式．

1 基本概念

定义1若图G有一个1-正则生成子图P，则称这个生成子图P为图G的完美对集．

定义2设图G是一个有完美对集的图，若图G的两个完美对集P1和P2中有一条边不同，则称P1和P2是G的两个不同完美对集．

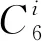
2 主要结果

定理1设图2-3-nC6的完美对集数为ρ(n)，则ρ(n)=3n+1．

证明显然{su12，u11v13，v11u13，v12u22，u21v23，v21u23，…，vn-1，2un2，un1vn3，vn1un3，vn2t}是图2-3-nC6的一个完美对集．因此，可设图2-3-nC6的完美对集数为ρ(n)．欲求ρ(n)的解析式，分别定义3个图G1、G2和G3，并求出它们的完美对集数的递推式．把路w1u2w3的端点w1、w3分别与图2-3-nC6顶点u11、u13各连接一条边，再把路w2u1w3的端点w2、w3分别与图2-3-nC6顶点u12、u13各连接一条边，最后删除图2-3-nC6的顶点s，这样产生的图记为G1，如图2所示．类似地定义图G2、G3，见图3、4．

显然{u1w2，u2w1，w3u13，u11v12，u12v11，v13u23，…，un1vn2，un2vn1，vn2t}是图G1的完美对集．容易判断图G2、G3有完美对集．显然G1≅G3．α(n)、β(n)分别表示图G1、G2完美对集的数目．则图G3的完美对集数为α(n)．

下面证明α(n)=β(n)．设图G1完美对集的集合为P，图G1含边u1w2、u1w3的完美对集集合分别记为P1、P2，则P1∩P2=∅，P=P1∪P2，故α(n)=|P|=|P1|+|P2|．

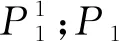
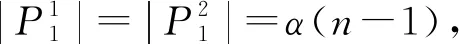
因为u1w3∈P2，所以u2w1，w2u12∈P2，由β(n)的定义可知，|P2|=β(n-1)．

因此，

α(n)=2α(n-1)+β(n-1)

(1)

设图G2完美对集的集合为M，图G2含边u1w2、u1w3的完美对集集合分别记为M1、M2，则M1∩M2=∅，M=M1∪M2，故β(n)=|M|=|M1|+|M2|．

因为u1w2∈M1，所以u2w1，w3u13∈M1，由α(n)的定义可知，|M1|=α(n-1)．

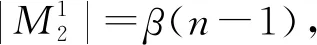
因此，

β(n)=2α(n-1)+β(n-1)

(2)

由式(1)和(2)可知，

α(n)=β(n)=3α(n-1)

(3)

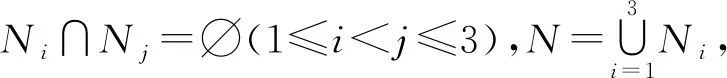
因为su11∈N1，所以su12，su13，u11v12，u11v13∉N1，因为G1≅G3，由α(n)的定义可知，|N1|=α(n-1)．

因为su12∈N2，所以su11，su13，u12v11，u12v13∉N2，由β(n)的定义可知，|N2|=β(n-1)=α(n-1)．

因为su13∈N3，所以su11，su12，u13v11，u13v12∉N3，由α(n)的定义可知，|N3|=α(n-1)．

综上所述，

ρ(n)=3α(n-1)

(4)

由式(3)和(4)，得ρ(n)=3n-1α(1)．

由图5知，α(1)=9，故ρ(n)=3n+1．证毕．

下面再给出图2-3-nC6的完美对集数为3n+1的一个组合证明．

事实上，饱和图2-3-nC6顶点s的完美对集的边有3种选择，分别是边su11、su12、su13，当边su1i(i=1，2，3)被选定，每个完美对集都要从4条边u1jv1k中选取2条边(j，k∈{1，2，3}，j≠i，k≠i)，也就是在圈u11v12u13v11u12v13u11上除边u1iv1j、u1iv1k(i，j，k互不相等)的4条边中选取不相邻的2条边，有3种选择；当u1jv1k中的2条边选定之后，边v11u21、v12u22、v13u23中有唯一确定的边在完美对集中；如此下去，每个圈ut1vt2ut3vt1ut2vt3ut1(t=1，2，…，n)中选取2条不相邻的边在完美对集中，都有3种选择，按乘法原理，共有3n+1种选择边的方法，因此图2-3-nC6的完美对集数为3n+1．

例1ρ(1)=9，图2-3-1×C6的9个不同完美对集见图6．

3 结 语

图的完美对集计数问题研究具有重要的理论价值和现实意义．但是，一般图的完美对集计数问题却是NP-难问题．本文方法研究了计算一般的有完美对集图的所有完美对集数的可能性．很多存在完美对集图都能利用本文方法求出它的完美对集数的递推式，由于高阶递推式的特征方程是一个高次代数方程，而一般的5次及以上代数方程没有根式解，一般的图很难求出它的完美对集数递推式的通解．但是，从应用角度来看，递推式更容易算出一个图的完美对集数．因此，本文方法为图的完美对集应用提供了有力支持．