目标引领 问题驱动 活动启智
2020-07-28陈燕军
陈燕军


【摘要】课堂除了知识与技能的掌握,更要注重在教学中促进学生的主体意识、创新精神和素养的发展,而有目标引领、有正向问题、有数学活动的课堂可以驱动学生激活旧知、独立思考、解决问题和提升素养。
【关键词】设计与思考;弧长和扇形的面积;素养
笔者参加了全市教学展示活动,且教学设计“弧长和扇形的面积”获得与会专家好评。本设计围绕“目标引领、问题驱动、活动启智”的思路展开,现将其设计和思考呈现如下。
一、设计简述
1.生活引学,激活旧知
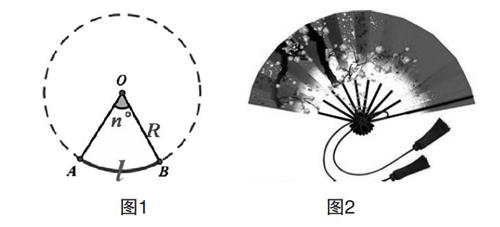
问题1:在小学,我们学过了圆和扇形,晓得扇形是圆的一部分(如图1)。请同学们回想,圆的周长公式、面积公式分别是什么?
设计意图:激活旧知,做好知识铺垫。
问题2:我们知道,如图2扇子是一个扇形,试指出该扇形的半径、圆心角、弧。那扇形的面积、弧长又分别是指什么呢?
设计意图:强化关键,明确弧是一段曲线,是圆周的一部分,弧长是这段曲线的展直长度。
问题3:将闭合的扇子徐徐打开,圆心角逐渐变大,在这个过程中,扇形弧长和扇形的面积如何随着圆心角的变化而变化?它们之间到底有什么样的关系呢?
设计意图:自然引入课题,并为后面的函数视角打下伏笔
2.问题驱动,活动启智
数学活动一:探索弧长计算公式
如图1,已知扇形的半径为R,圆心角度数为n,试求该扇形的弧长
问题1:当n为多少度时,扇形的弧长最容易求?举例并说明理由。
设计意图:研究问题,常常是从最简单或者最特殊的情形入手的。引导学生从圆心角为180。(半圆周)、90。(四分之一圆周)、450等简单情形入手。
问题2:上述例子我们是根据什么来求弧长的?能给我们以什么启示?
设计意图:引导学生感悟局部与整体之间的关系 弧长占整个圆周长的几分之几,圆心角是圆周角(360。)的几分之几。
问题3:如果圆心角度数为n,又如何来求此扇形的弧长?试写出推导过程。
设计意图:通过特殊到一般、局部与整体之间的关系,学生由1。的弧长推导得到n。的弧长,经历自主推导探索,得
问题4:观察公式,当半径R为定值时,弧长R与圆心角n是什么函数关系?当圆心角度数n为定值时,弧长,与半径R又是什么函数关系呢?弧长、半径、圆心角三个量需要知道其中任意几个量,能求出其他的量吗?
设计意图:弧长公式的再认识和强化 呼应前面的“徐徐打开”,渗透函数观点和方程观点
数学活动二:探索扇形面积计算公式
已知扇形半径为R,圆心角度数为n,试求该扇形面积s。
问题1:经历了弧长公式的探究,你能否设计一个探究扇形面积公式的方案?
设计意图:同样的思路,同样的过程,该方案由学生自主设计,讨论交流,展示结论,得到公式。渗透类比思想,进一步扩大思维含量。
问题2:从前面扇子徐徐打开的过程可以知道,扇形的面积同样随着弧长的变大而变大。是否可以用扇形的弧长和半径表示该扇形的面积呢?试写出推导过程。
设计意图:学生通过自主推导,得到公式将
4反思悟学,课后作业
略
二、设计思考
结合教学实际,笔者从以下三个方面谈自己的思考。
1.设计的思路
总体遵循“目标引领、问题驱动、活动启智”的思路,基于发展学生数学素养设计教学,着力提升素养开展教学,学生在学习数学知识的同时提升数学素养。
环节设计上,采用“目标引领”。按照教学目标,将具体的教学内容分解为具体的教学任务,如问题的提出、问题的探究、公式的认识、公式的应用等,与这些任务对应,设计了相应的教学环节,力求突出重点,直达本质,尽量减少认知负荷,把更多的时间放在更有价值的地方。
环节落实上,采用“问题驱动”。从“问什么、怎样问、向谁问”三个方面入手,重点环节设计系列问题,每个问题都有明确的目标指向,每个问题都有一定的思维空间,让学生在独立思考和解決问题的过程中形成相关知识。设计时,尤其关注了“得出结论的难易”与“思维空间的大小”之间的平衡点。
知识探索上,采用“活动启智”。数学教学应该是数学活动的教学。活动一,教师精心设计正向问题,开展引导式的数学探究活动;活动二,教师完全放手,让学生自主设计探索方案,开展创新式的数学设计活动。
2.目标的达成
本设计达成教学目标的桥梁是数学思考与问题解决。
按照教学目标,以问题串来驱动目标的达成。如“当n为多少度时,扇形的弧长最容易求?”问题起点低,直指目标,有数学思维,学生通过特殊到一般、局部与整体的关系自主推导得到弧长公式。接着学生能类比探索弧长的方案设计出探索扇形的面积方案,得到扇形的面积公式。
整个探究过程学生领悟到了数形结合、类比、转化、特殊到一般的数学思想,渗透了函数观点,让学生感悟到“知二求三”的方程观点。学生人人参与,不同的学生在课堂上获得不同的数学发展。
3.素养的提升
本节课不仅教给学生运用公式来解决几个数学问题,更关注探究的过程与方法、思维与素养。教学紧紧围绕素养设计问题,问题起点低,入口宽,且具有一定思考空间,达到直指目标的效果。整节课发展了学生几何直观、逻辑推理等素养,学生感悟了数学结合、类比、转化等重要数学思想,而问题的解决,学生的发言,则提升了学生独立思考、自主探索、合作交流和语言表达等终生必需的品格和关键能力。学生在课堂中积累的发现问题、思考问题、提出问题、设计方案、解决问题等经验,为今后探究和解决数学问题提供了宝贵的经验和万法。
【参考文献】
[1]金敏.联系蕴结构,探究促发展[I]中学数学教学参考(中旬),2019(4):5-8
[2]刘春江文化视角下素养立意的初中数学概念教学[J]中学数学教学参考(中旬),2019(4):9—12
[3]陈华忠问题驱动,落实数学核心素养[J]小学教学设计,2019(14)
