外界条件对中空结构物内爆冲击波的影响

孟令存，闫 明，杜志鹏，张 磊

（1. 沈阳工业大学机械工程学院，辽宁 沈阳 110870；2. 海军研究院，北京 100161）

中空结构物在深水环境下工作时，表面将会承受高静水压力，当中空结构物突然被压溃，高压水流向压溃中心汇聚相撞，形成内爆（Implosion）[1-2]，产生内爆冲击波，对周围物体造成破坏。2014 年美国深海科研潜艇在深海工作时，中空结构的外部工作设备在静水压下被压溃引发内爆，对潜艇壳体造成损伤，使其“遇难”。在中微子探测领域[3-4]，由玻璃制成的具有中空结构的光电倍增管（Photomultiplier tube，PMT）是中微子探测的核心部件，工作在深水环境时容易发生内爆。2001 年，日本“超级神冈”中微子试验站发生PMT 连锁爆炸事故，炸毁近8 000 个PMT，直接经济损失达3 000 万美元[5]。除此之外，其他水下工作设备如管道、照明灯、摄像机等都有可能发生内爆，因此内爆机理研究具有重要意义。

国内外学者针对水下内爆问题开展了诸多研究。美国海军作战中心（NSWC）[6]在装有水的压力罐中进行了圆柱壳的水下内爆实验，得到了铝制圆柱壳的内爆冲击波压力曲线，并结合仿真研究了圆柱壳的内爆冲击波压力曲线的主要特征；Diwan 等[7]在压力罐中对PMT 进行了2 次水下内爆试验，得到了PMT 内爆发生过程及内爆冲击波压力曲线，并利用任意拉格朗日欧拉（ALE）方法对PMT 内爆进行了仿真，得到的仿真结果与试验结果吻合较好；杜志鹏等[8]将水下爆炸气泡动力学与水下内爆相结合，基于能量守恒关系，推导出不可压缩流体中球形容器内爆理论模型；黄治新等[9]根据应力波原理，提出了利用大型压力罐进行内爆试验的方法，并通过此方法测得了PMT 内爆冲击波。

上述研究主要针对特定结构的圆柱壳、PMT 进行试验和数值模拟研究，没有考虑静水压、真空体积对中空结构物内爆的影响。本研究拟开展PMT 水下内爆试验，以验证ABAQUS 软件CEL 耦合计算方法模拟水下内爆的准确性，并通过有限元模拟方式探究外界静水压力、真空体积对内爆冲击波的影响规律，为深入分析中空结构物的水下内爆提供参考。

1 PMT 内爆试验与数值模拟

1.1 PMT 水下内爆试验

PMT 实物见图1，其形状如灯泡，总高度0.700 m，头部球体直径0.508 m，尾部圆柱直径0.100 m；其外壳材料为玻璃，厚度为5 mm，内部真空度为10-4Pa。PMT 水下内爆试验装置为直径3 m、长度5 m、壁厚30 mm 的圆柱形钢制压力罐，其示意图见图2。压力罐侧面设有透明视窗，用于照明并放置高速摄影设备，可清晰地记录内爆全过程；压力罐内部设有工作平台，工作平台上放置液压式挤压装置，用于安装和引爆PMT。受试验装置尺寸限制，将压力罐装入水时，无法模拟PMT 在50 m 水深的工作环境，为此利用外置空压机对压力罐内施加0.5 MPa 压力进行模拟。通常情况下，采用水中压力值代表冲击波压力，故在试验过程中主要测量水中压力值。试验前，压力罐内共布置4 个PCB 动水压传感器，测点F1位于PMT 正上方，距PMT 中心0.41 m；测点F2位于PMT 赤道平面靠近压力罐入口处，距PMT 中心0.55 m；测点F3、测点F4位于PMT 赤道平面远离压力罐入口处，分别距PMT 中心0.55 和1.35 m。试验时，液压装置挤压PMT 发生内爆，试验成功测得PMT 水下内爆过程和压力数据。

图 1 PMT 实物Fig. 1 Picture of actual PMT

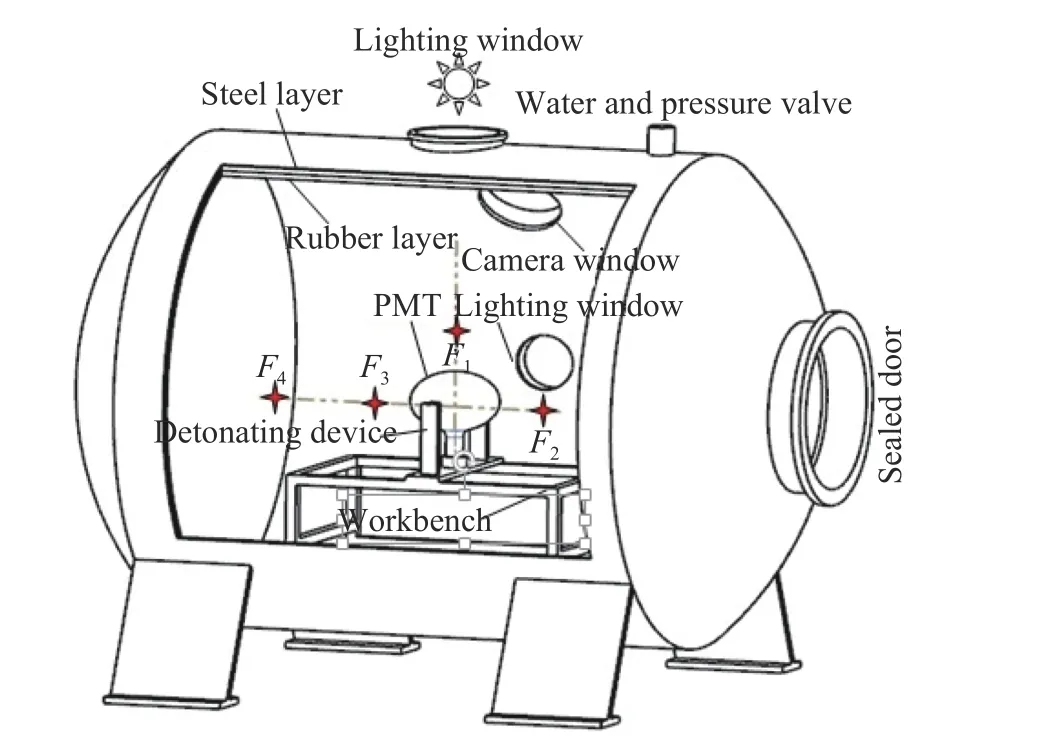
图 2 压力罐示意图Fig. 2 Schematic of the pressure tank

1.2 水下内爆试验结果分析

完成PMT 内爆试验后，根据高速摄影所记录的影像，对内爆过程进行详细分析。将PMT 水下内爆发生时间点记为零时刻（t = 0 ms），图3 为PMT 发生内爆典型特征时刻的图像。可以看出，PMT 内爆过程可分为4 个典型阶段：（1）挤压阶段（-16.00～-14.00 ms），挤压装置挤压PMT 使玻璃外壳产生微小变形，挤压装置附近玻璃外壳亮点缩小；（2）裂纹传播阶段（-14.00～-8.00 ms），PMT 玻璃外壳在-12.33 ms产生初始裂纹，-8.00 ms 裂纹迅速传播至整个球面；（3）整体压溃阶段（-8.00～0 ms），PMT 玻璃外壳在0 ms完全被压溃，碎片迅速向中心运动，各方向水流发生碰撞，产生内爆冲击波；（4）冲击波传播阶段（0 ms以后），玻璃碎片迅速向外飞散，冲击波以近似声速向外传播，图像出现黑色斑点，这是因为冲击波到达罐壁时发生反射，反射波与入射波发生叠加产生了空化气泡。上述阶段划分充分展现了PMT 水下内爆发生过程及内爆冲击波的产生过程，对水下内爆数值模拟具有一定的指导意义。

1.3 PMT 水下内爆数值模拟

基于PMT 水下内爆的试验结果，对PMT 水下内爆进行数值模拟。由试验结果可知，在PMT 内爆过程中，从裂纹产生到内爆发生共经历了14 ms，具有瞬时性；此外，考虑到PMT 所处的环境，在内爆发生过程中还会存在流体与玻璃之间的耦合作用。根据上述分析，可利用有限元软件ABAQUS中的CEL 算法对PMT 水下内爆进行数值模拟。

图 3 PMT 内爆过程Fig. 3 Implosion process of PMT

图4 为PMT 内爆有限元模型中部截面图，整个球体水域采用欧拉单元（EC3D8R），中间网格密度大，外部网格密度小，以减小计算时间。红色部分的欧拉单元赋予水材料属性，水采用Grüneisen状态方程描述，密度为1.0 g/cm3，波速为1 480 m/s，黏度为1×10-3Pa·s，在水域中利用初始应力场施加0.5 MPa 的初始静压力，且在水域外边界设置冲击波无反射、流体自由流入和流出的边界条件，以模拟无限水域。蓝色部分的欧拉网格赋予真空材料属性。红色部分与蓝色部分交界处为PMT 玻璃外壳，采用六面体拉格朗日单元（C3D8R），材料参数如下：密度为2 230 kg/m3，弹性模量为2.77 GPa，泊松比为0.376，断裂极限为40 MPa，玻璃失效位移为0.1 μm。在模型中输出与试验相同测点的压力值，用于后期数据的相互验证及对比分析。数值模拟开始时，对PMT 外表面局部区域施加瞬时压力，以模拟液压装置对PMT 的挤压，使得PMT 破碎，从而发生水下内爆。

欧拉网格具有与材料完全隔离的特性，根据网格内材料的占比不同，会呈现不同的网格颜色。当网格呈红色时，欧拉网格中水的占比为100%，即水填满整个网格；当网格呈蓝色时，水的占比为零，即没有水填充到网格。图5 为数值模拟得到的流场运动过程。当PMT 受到挤压时，局部发生破碎，水流从挤压位置涌入PMT 内，导致PMT 的玻璃外壳全部压溃，各方向水流迅速向PMT 中心处汇聚并发生碰撞，产生冲击波。整个PMT 内爆过程共经历13.6 ms，与高速摄像拍摄的内爆过程及发生内爆的时间相近，说明采用CEL 耦合计算方法能够准确地模拟PMT 发生内爆时水域流场变化过程。

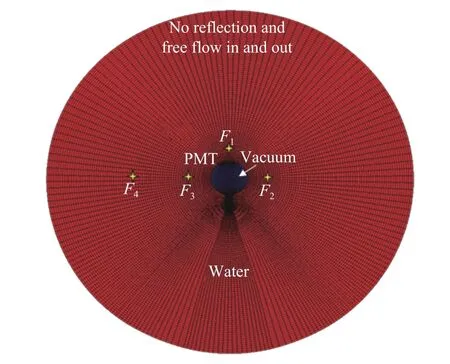
图 4 PMT 内爆仿真模型Fig. 4 Implosion simulation model of PMT

图 5 水域流场变化过程Fig. 5 Change process of flow field in the water

1.4 试验与数值模拟结果对比分析

为进一步验证PMT 内爆数值模拟方法的正确性，对数值模拟和试验的压力测点数据进行对比分析。由于试验中使用的是动压传感器，无法测出水中的初始静压力，所以将试验中的压力值均增加0.5 MPa，以模拟所受的静水压作用。进一步调整试验压力值的起始位置，使试验与数值模拟压力峰值相对应。图6 为各测点的内爆冲击波压力对比曲线，可以看出：无论是试验还是数值模拟，内爆冲击波压力峰值均较高，脉宽较小。数值模拟的压力曲线在零时刻附近出现振荡，这是由数值模拟过程中测点处的能量平衡引起的。在未达到压力峰值的曲线段，数值模拟与试验中均出现微弱压力降，这是由PMT 玻璃外壳完全破碎后水流内涌存在速度势导致的。达到压力峰值后，数值模拟曲线快速恢复到平衡位置，而试验曲线出现振荡式衰减，这是由于数值模拟中设置了无反射边界的水域条件，而试验中由于压力罐尺寸的限制，罐壁对冲击波具有一定的反射作用。总体而言，数值模拟得到的内爆冲击波脉宽、峰值与试验结果吻合较好。

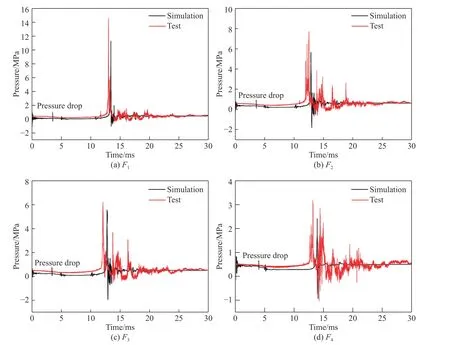
图 6 内爆压力对比曲线Fig. 6 Comparison curves of implosion pressure

进一步对试验与数值模拟得到的压力峰值进行对比，结果列于表1。各测点峰值中，模拟峰值普遍小于试验峰值，这是由于数值模拟中玻璃材料本构方程与实际存在差异，致使玻璃的破碎速率不同，从而对内爆冲击波压力峰值产生一定的影响；此外，模拟时模型网格大小对结果精度也有一定的影响，使得冲击波压力峰值降低，但整体平均误差为20.8%，满足实际工程需求。选取内爆试验压力测点F1的压力数据进行积分，得到比冲量峰值为2 700 Pa·s，该能量相当于50 g 标准TNT 炸药按Geers & Hunter 水下爆炸理论公式计算所得的能量。

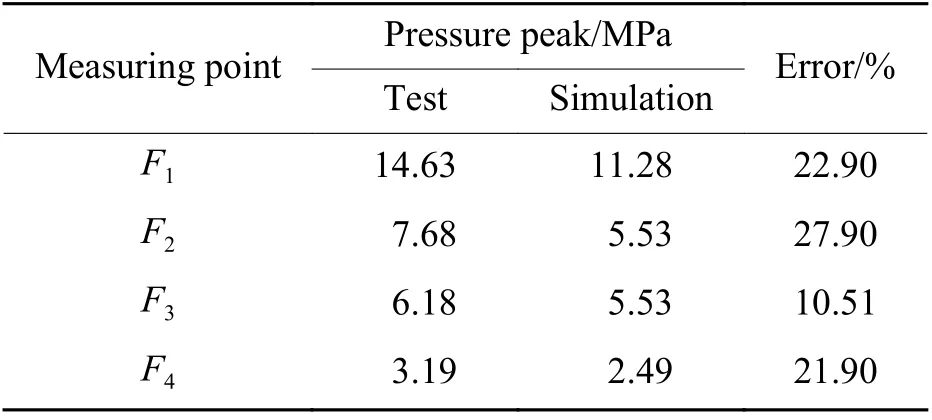
表 1 试验和模拟得到的冲击波压力峰值对比Table 1 Comparison of tested and simulated shock wave pressure peaks

2 内爆冲击波影响因素分析

在PMT 水下内爆数值模拟方法正确建立的基础上，利用数值模拟对内爆冲击波的影响因素进行研究。为了方便建模，采用体积等效的方式将PMT 等效为直径0.5 m 的真空球体。

2.1 静水压力的影响

水下内爆发生时PMT 玻璃外壳瞬间破碎，水流急速碰撞产生冲击波。为了简化计算，仅建立水域及真空球体区域模型。图7 为建立的有限元简化模型。外部水域直径为5 m，内部真空球体直径为0.5 m；共设置5 个压力测点，编号为S1～S5，分别距球心0.25、0.35、0.45、0.55、0.65 m；简化模型的材料本构、边界条件、载荷等计算参数保持不变；根据PMT 的实际工作环境，共设置了静水压分别为0.3、0.4、0.5、0.6 及0.7 MPa 的5 种内爆工况进行数值模拟。

图8 显示了0.5 MPa 静水压作用下水域流场的变化过程。可以看出：计算开始时，水流迅速向中心流动，初始阶段，水流速度由零开始进行加速，水流总体运动较慢；随着时间的延长，水流获得了较大的运动速度，向中心加快运动，经历10.25 ms 后，水流发生碰撞产生内爆冲击波。

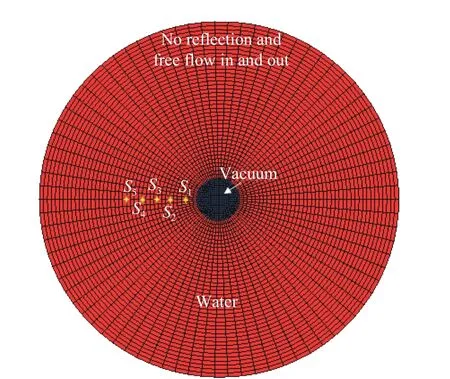
图 7 内爆简化模型Fig. 7 Simplified model of implosion

图 8 内爆水流涌入过程Fig. 8 Water influx of implosion

进一步对测点的压力情况进行分析，图9 为真空球体在5 种工况下，水流高速碰撞产生冲击波，各测点的冲击波压力时程曲线。可以看出：各工况下压力曲线的变化趋势大致相同，首先在短时间内达到内爆冲击波峰值，随后压力值出现了不同程度的振荡，最后均稳定为零压力，且各测点的振荡形式相似；同一静水压下，随着测点距离的增大，内爆冲击波压力峰值显著减小。比较各工况下同一测点测得的冲击波压力峰值对应的时间可知，随着静水压力的增加，内爆发生的时刻提前。

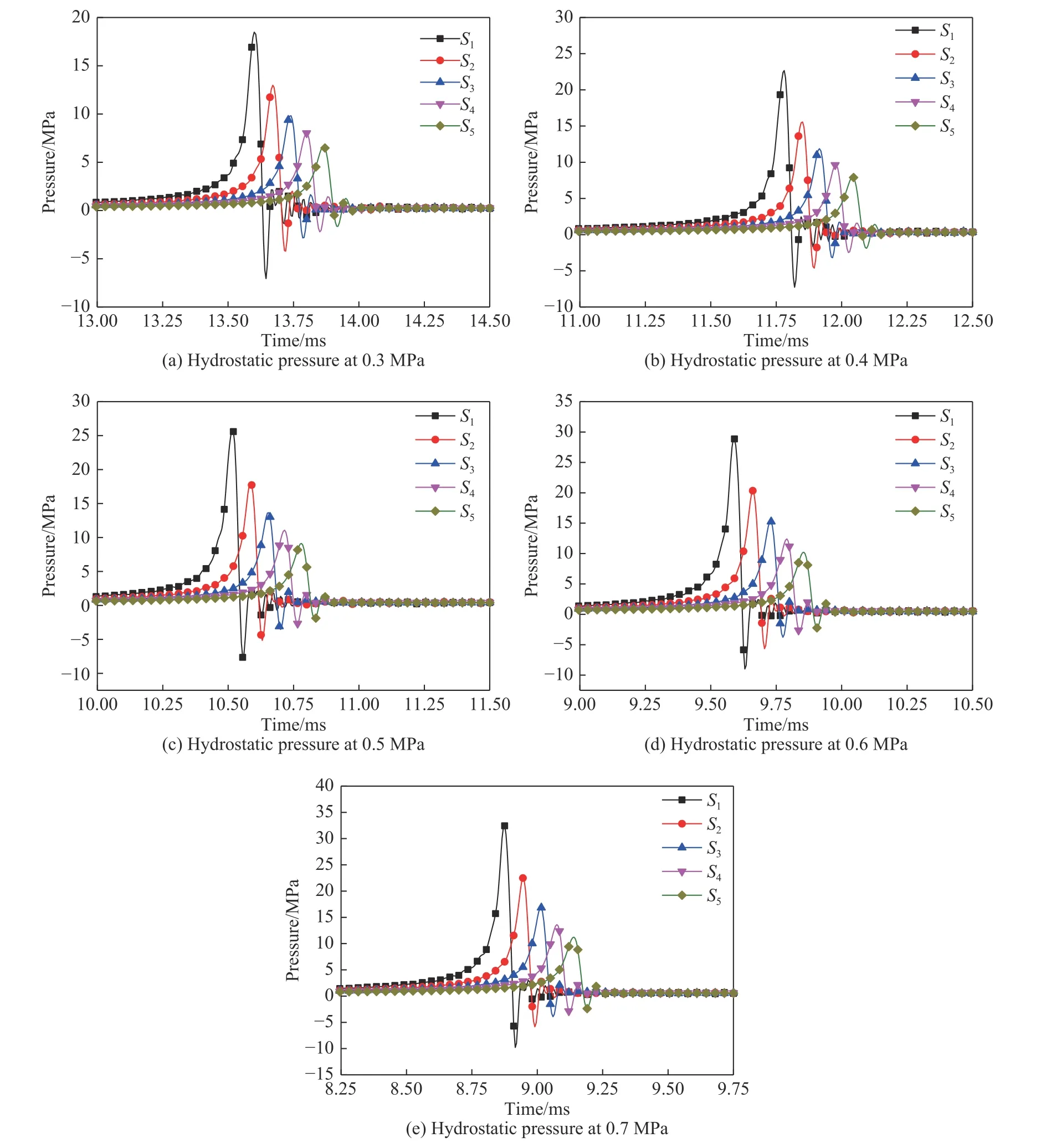
图 9 压力时程曲线Fig. 9 Curves of pressure varied with time

对图9 中的冲击波压力峰值进行分析，以测点距离为横坐标，各测点冲击波压力峰值为纵坐标，绘制出各静水压下冲击波压力峰值随测点距离的变化规律，如图10（a）所示。分析发现，同一静水压下，冲击波压力峰值pm随测点距离x 的变化规律可用指数函数pm= axb进行拟合，拟合结果如表2 所示。冲击波峰值衰减指数b 在-1.067～-1.107 范围，同比炸药的水下爆炸冲击波传播衰减指数（1.18）偏小。以冲击波压力峰值的10%对应的两个时刻之间的差值定义为内爆冲击波脉宽，选取0.3 MPa 静水压下各测点脉宽进行讨论，脉宽随测点距离变化曲线如图10（b）所示，脉宽随距离的增大缓慢增大。

图 10 冲击波压力峰值和脉宽随测点距离变化曲线Fig. 10 Curves of shock wave peak and pulse width with measuring point distance

为准确分析静水压对内爆冲击波的影响规律，以静水压为横坐标，测点的冲击波压力峰值为纵坐标，对图9 中各工况下不同测点冲击波压力峰值重新进行统计，如图11（a）所示。可以看出，对于同一测点，冲击波峰值压力pm随外界静水压力ph呈线性增长趋势，可用函数pm= cph+ d 对其进行线性拟合，所得拟合系数值如表3 所示，斜率c 随测点距离的增大而减小，即距离内爆中心越远，冲击波压力峰值变化越平缓。选取各静水压下0.25 m 处测点脉宽进行讨论，脉宽随静水压变化曲线如图11（b）所示，脉宽随静水压力的增加基本保持不变。

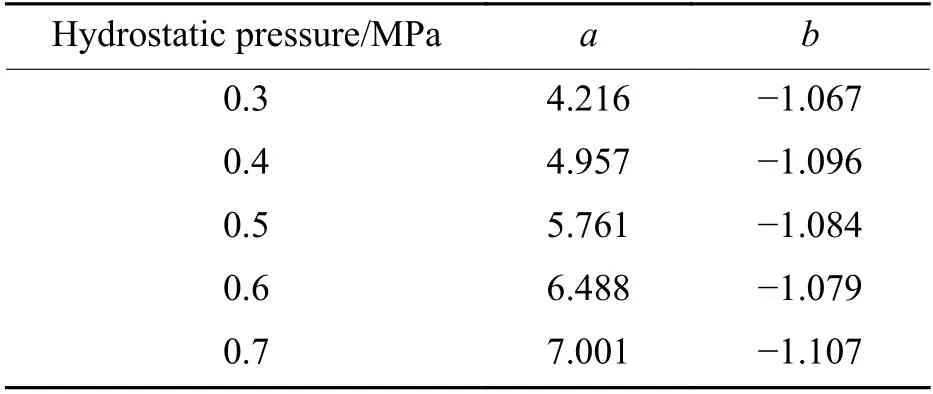
表 2 拟合系数值Table 2 Fitting coefficient values

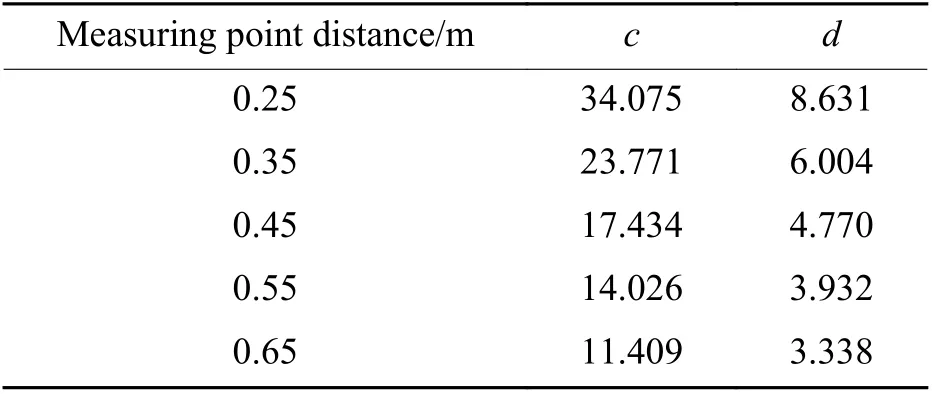
表 3 拟合系数值Table 3 Fitting coefficient values

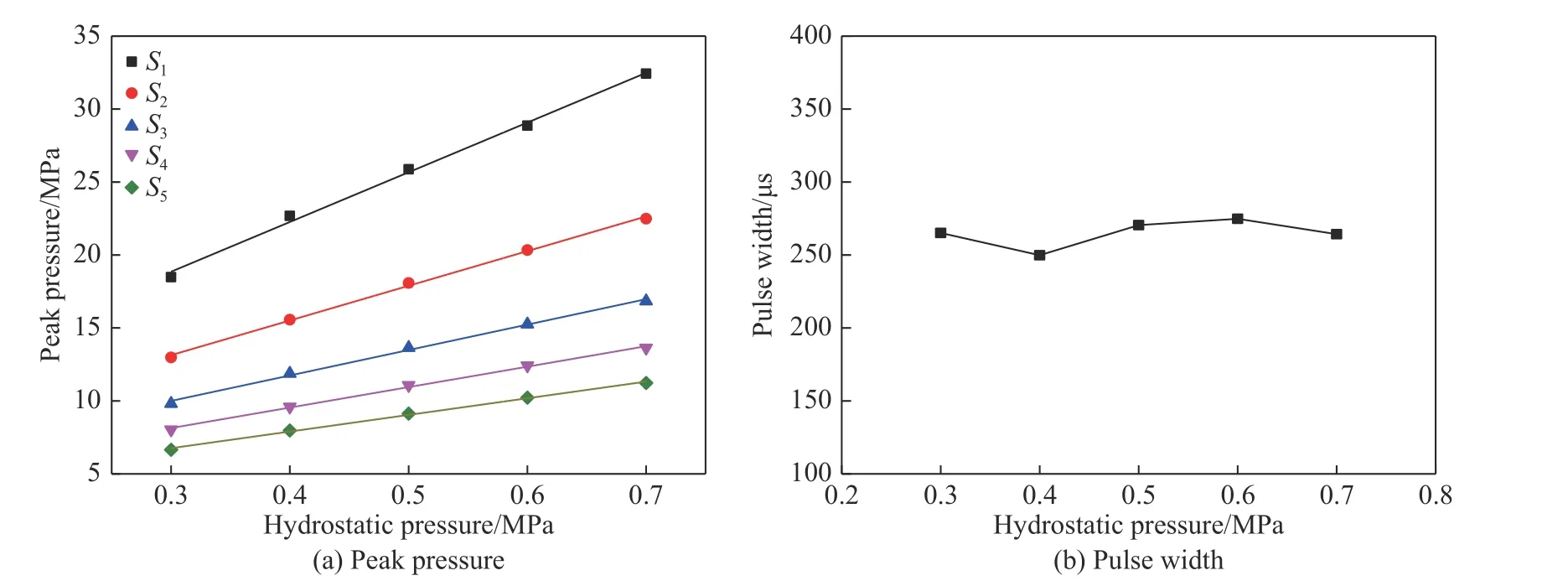
图 11 冲击波压力峰值和脉宽随静水压变化曲线Fig. 11 Curves of shock wave peak and pulse width with hydrostatic pressure

2.2 真空体积的影响

将静水压设为0.5 MPa，选取与2.1 节相同的压力测点，真空球体半径依次修改为0.15、0.20、0.25、0.30 及0.35 m，进行5 种工况下的内爆数值模拟，研究真空体积对内爆冲击波压力峰值的影响规律。图12 为不同工况各测点的内爆冲击波压力曲线。从图12 可以看出：真空球体半径越大，内爆发生的时刻延后，冲击波峰值越大。

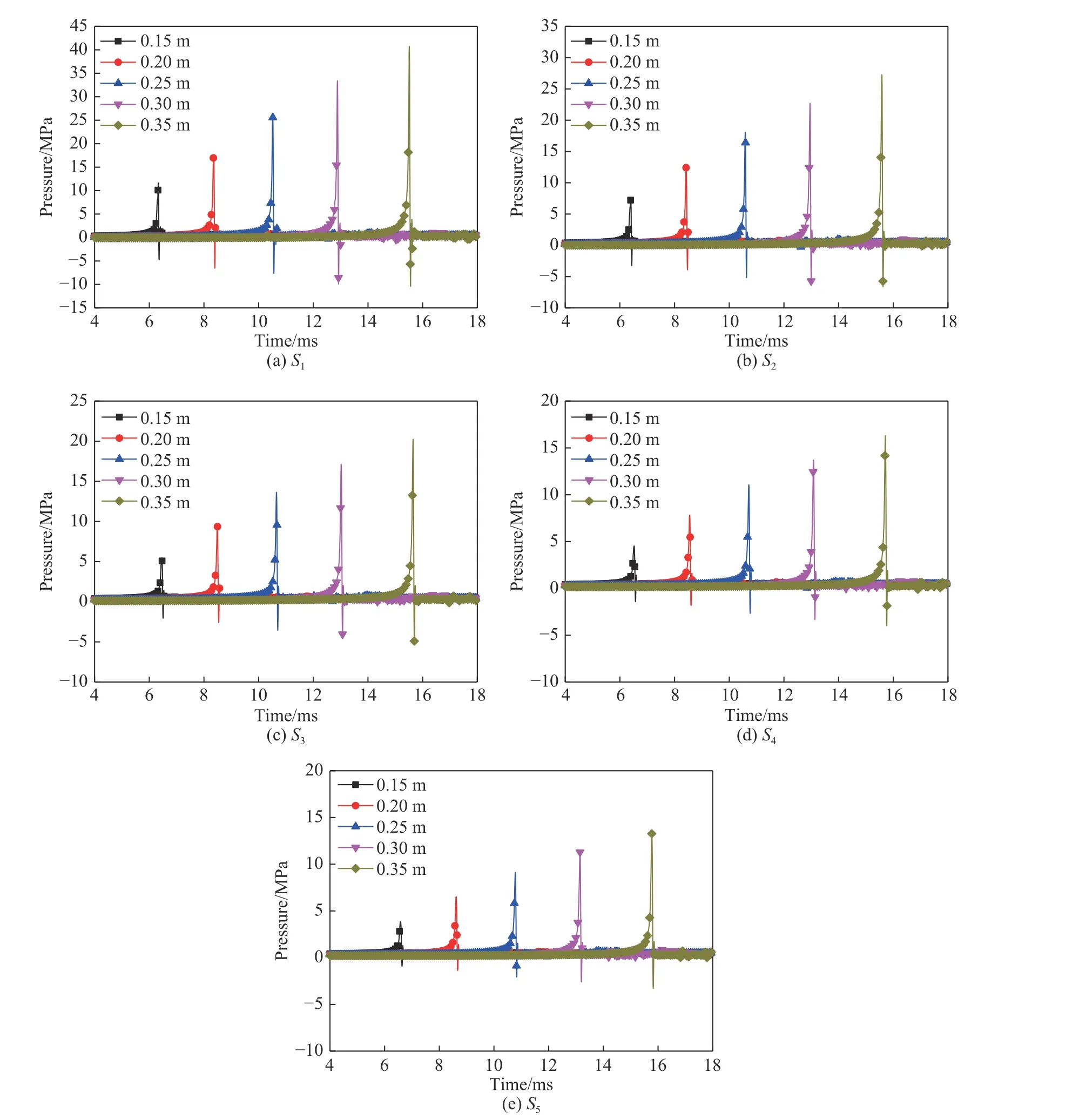
图 12 不同真空球体半径的冲击波压力时域曲线Fig. 12 Curves of shock wave pressure with time under different vacuum sphere radii

对图12 中的冲击波压力峰值数据进行统计，以真空球体半径为横坐标，冲击波压力峰值为纵坐标，绘制图像如图13(a)所示。

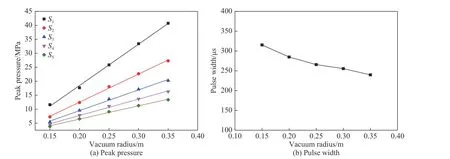
图 13 冲击波压力峰值和脉宽随真空半径变化曲线Fig. 13 Curves of shock wave peak and pulse width with vacuum radius

从图13(a)可以看出，冲击波压力峰值pm随真空球体半径r 呈线性变化。利用pm= mr + n 进行线性拟合，拟合系数值列于表4。分析可得，当距内爆中心位置一定时，冲击波压力峰值随真空体积的增大呈线性增大，且距离内爆中心越近的位置增长越快。选取各工况下0.25 m 处测点进行脉宽讨论，脉宽随真空半径变化曲线如图13(b)所示，脉宽随真空半径的增大缓慢降低。

表 4 拟合系数值Table 4 Fitting coefficient values

3 结 论

（1）对比PMT 内爆试验与数值模拟结果可知，ABAQUS 的CEL 数值模拟方法在模拟水下内爆发生过程、水域流场变化过程、冲击波压力峰值和脉宽等方面具有较高的模拟精度，能够准确、全面地模拟PMT 内爆的物理过程。

（2）通过对不同静水压力下的内爆进行数值模拟，得到了静水压力对内爆的影响规律：内爆发生的时刻随静水压力的增加而提前；内爆产生的冲击波压力峰值随测点距离增大呈指数衰减，且衰减系数比水下炸药爆炸冲击波衰减系数小；同一位置的内爆冲击波压力峰值随静水压力增加呈线性增长趋势，且距离内爆中心越远，冲击波压力峰值增长越缓慢；冲击波脉宽随静水压力的增加基本保持不变。

（3）通过对不同真空体积的内爆进行模拟，得到了真空体积对内爆的影响规律：内爆发生时刻随着真空体积的增大而延后；同一位置的内爆冲击波峰值随真空球体体积的增大呈线性增长，且距离内爆中心越近，冲击波峰值变化越快；冲击波脉宽随真空半径的增大缓慢降低。