CuS2 的高压拉曼光谱和X 射线衍射

姜 峰，赵慧芳，谢亚飞，姜昌国，谭大勇，肖万生

（1. 中国科学院广州地球化学研究所矿物学与成矿学重点实验室，广东 广州 510640；2. 广东省矿物物理与材料研究开发重点实验室，广东 广州 510640；3. 中国科学院大学，北京 100049）

黄铁矿结构（Pa3，Z = 4）是MX2型化合物的一种典型结构，原型为天然矿物黄铁矿（FeS2）。在该立方结构中，M 原子占据4a（0, 0, 0）位置，X 原子占据8c（u, u, u）位置，形成共角顶的AB6配位八面体[1]，如图1 所示。一些二硫化物MS2（M = Mn，Fe，Co，Ni，Cu，Zn，Ru，Os 等）[2-4]和二氧化物MO2（M = Be，Mg，Zn，Cd，Na 等）[5-6]均能够结晶成黄铁矿结构。另外，黄铁矿结构也是许多二氧化物和二氮化物在高压下的稳定多形，如SiO2、GeO2、SnO2、PbO2、FeO2、RuO2、OsO2、IrO2、PtO2、PtN2、PdN2等[7-9]。由于Fe 和SiO2是地球内部的重要组成元素和化合物，深入研究高压下黄铁矿型结构在地球科学和材料科学的发展过程中具有重要意义。例如，近期黄铁矿型结构FeO2和FeO2Hx的高温高压实验和理论研究进展[10-11]为理解下地幔环境中各种元素的化学性质和原子间的相互作用提供了新视角。

作为黄铁矿结构的典型代表，过渡金属二硫化物MS2（M = Mn，Fe，Co，Ni，Cu 等）由于具有良好的光电性质和催化性能被广泛地研究和应用，其高压行为（如高压稳定性、结构相变和金属-绝缘体转变等）也受到高度关注[12-16]。同时，过渡金属二硫化物还可以成为地球深部和气态巨行星内部SiO2等重要矿物的类比研究对象[17]，有利于发现SiO2等黄铁矿结构的高压多形，并了解这些高压多形的物理化学性质。

与其他黄铁矿结构二硫化物不同，CuS2需要在高温高压条件下才能合成[18-19]，导致相关研究相对较少。以CuS2为主要组成成分的天然矿物黑硫铜镍矿（Cu，Ni，Fe）S2需要Ni、Fe 等类质同像替代进入晶格才能保持稳定[20]。CuS2是一种深紫色晶体，具有金属导电性[21]，并在低温下显示超导电性[22]，King 等[23]对高温高压合成的CuS2单晶进行了详细的晶体结构研究，并与MS2（M = Mn，Fe，Co，Ni）等晶体结构参数和MS6八面体畸变程度进行比较，认为CuS2中Cu 的价态为+2 价。然而，CuS2的多种光谱和理论研究认为Cu 为+1 价态[21,24-26]。晶体化学与光谱学测量结果之间的矛盾或许隐含有价值的科学信息。

据相关研究报道，迄今只有Hupen 等[27]对CuS2开展过高压原位研究工作。Hupen 等利用同步辐射能量色散X 射线衍射技术在0～6 GPa 压力范围对CuS2开展原位测量，认为黄铁矿型CuS2在约1 GPa 压力下会发生向白铁矿结构（Pnnm）的可逆相变。白铁矿结构与文献中常见的CaCl2结构等型[4,28]，而对于大多数MX2化合物的高压结构演化来说，CaCl2结构是黄铁矿结构的低压相[7,29]。因此，CuS2相变还需要更高精度的高压X 射线衍射及其他高压测量方法证实。

本研究利用金刚石压腔高压装置开展了CuS2的高温高压合成及其高压拉曼光谱和X 射线衍射测试。黄铁矿结构CuS2可在6～33 GPa 压力范围，通过电阻外加热方式（800 K）和激光加热方式（1 500～2 000 K）合成，并对其进行高压拉曼光谱和X 射线衍射测试，探索黄铁矿结构CuS2在0～30 GPa压力范围的结构稳定性。同时，对黄铁矿结构CuS2开展第一性原理理论计算，并将计算结果与实验结果进行对比验证。研究结果对于认识 Cu 在地球深部环境中的价态和赋存形式具有重要意义。

图 1 黄铁矿（Pa3）MX2 晶体结构示意图（蓝色大球和黄色小球分别表示M 和X 原子）Fig. 1 Pyrite-type(Pa3) MX2 crystal structure （M and X atoms are shown as big blue and small yellow spheres, respectively.）

1 实验技术和理论计算方法

将分析纯化学试剂Cu、S 以及CuS、S 分别按化学计量比1∶2 和1∶1 称量，并在玛瑙研钵中研磨1.5 h充分混合，作为合成CuS2的初始反应物。高温高压合成实验采用两种类型的金刚石压腔（DAC）装置：一种为可与显微激光加热系统连接的对称型DAC 装置（LH-DAC），光谱仪接收样品热辐射谱，并用黑体辐射公式拟合实验温度；另一种为电阻丝加热的DAC 装置（RH-DAC），用NiCr-NiAl 热电偶测量实验温度。两种DAC 装置的金刚石对顶砧砧面直径均为300 μm。实验采用T301 不锈钢片封垫，预压厚度约35 μm，用电火花打孔器在中心钻一个直径105 μm 的小孔作为样品腔。共进行了4 组CuS2的合成实验。激光加热实验（Exp1 和Exp2）初始样品均为Cu+2S 混合物，隔热层和压力介质为KCl，采用“三明治”方式装样，并加入红宝石微粒用于测压[30]，实验压力分别为7.0 和34.1 GPa，实验温度1 500～2 000 K。电阻丝加热实验的装样方法与激光加热实验相同，实验样品分别为Cu+2S（Exp3）和CuS+S（Exp4），采用SrB4O7∶Sm2+作压标[31]，实验压力分别为12.4 和16.6 GPa，实验温度为800 K，恒温约1 h。通过拉曼光谱鉴定4 组实验合成产物。

拉曼光谱测试采用Renishaw 2000 型显微共聚焦拉曼光谱仪。选用波长为532 nm 的激光作为激发光源，用20 × 物镜聚焦激光光斑，样品处光斑大小为3 μm × 3 μm。采用背反射方式收集样品信号，通过1 800 线每毫米光栅分光，由热电冷却的CCD 探测器采集信号。采谱波段范围100～800 cm-1，光谱分辨率1 cm-1，采谱时间40 s。高压原位角色散X 射线衍射实验在中国科学院高能物理研究所同步辐射装置4W2 线站开展。入射X 射线波长λ 为0.619 9 Å，光束被聚焦到约60 μm × 20 μm 大小。Pilatus 探测器收集衍射图谱，样品到探测器的距离由CeO2标定。利用Fit2D 软件[32]对采集的二维衍射图进行积分处理。Birch-Murnagham 状态方程参数由EosFit7 程序[33]拟合得到。运用GSAS-II 软件[34]对6.2 GPa 压力点的粉末衍射谱进行Rietveld 结构精修。

CuS2的第一性原理理论计算采用Material Studio 软件的CASTEP 计算模块。运用Perdew-Burke-Ernzerhof 泛函的广义梯度近似（GGA）方法估算交换相关能[35]。赝势选择OTFG 超软赝势，截断能设置为700 eV，第一布里渊区k 点取样为6 × 6 × 6 网格。为确保较好的收敛，能量、最大力场、最大应力和最大位移分别为5.0 × 10-6eV/atom、0.01 eV/Å、0.02 GPa 和5.0 × 10-4Å。

2 结果和讨论

2.1 黄铁矿结构CuS2 的高温高压合成

图2 为4 组合成实验高温处理前后的拉曼光谱。加热前，由于CuS 高压非晶化，在约15 GPa 实验压力下基本难以观测到拉曼峰，而Cu 单质无拉曼活性峰，因此4 组实验在反应前测得的拉曼光谱均属于单质S 的高压相[36-37]。加热后，4 组实验都得到由3 个拉曼峰组成的全新谱图，表明实验样品在不同压力经不同温度处理后得到了相同的新相。新相在常温常压下的3 个拉曼峰频率(ω0)在表1 列出，与Anastassakis 等[38]给出的黄铁矿结构CuS2的拉曼峰位和峰形特征基本一致，可初步确认实验合成的新相为黄铁矿结构CuS2，后述同步辐射X 射线衍射实验结果将进一步证实。已有的CuS2合成实验条件基本均在7.0 GPa、1 500 K 温压范围以内[2,18-19,21]，本次4 组实验在更宽范围的温压条件下均合成出黄铁矿结构CuS2，拓展了CuS2的合成温压范围，同时说明了CuS2在34.1 GPa、2 000 K 温压范围内是热力学稳定态。

图 2 不同条件下4 组实验反应前后的特征拉曼光谱（LH 和RH 分别代表激光加温和电阻丝加温，4 组实验中加温前所测拉曼信号均为单质硫的高压相，加温后产物为黄铁矿结构CuS2）Fig. 2 Raman spectra of the four experiments at different conditions before and after reaction （LH and RH represent laser heating and resistance heating, respectively. Before heating, all the Raman peaks in four experiments belong to the high-pressure phase of elemental sulfur. After heating, the reaction products are pyrite structure CuS2.）

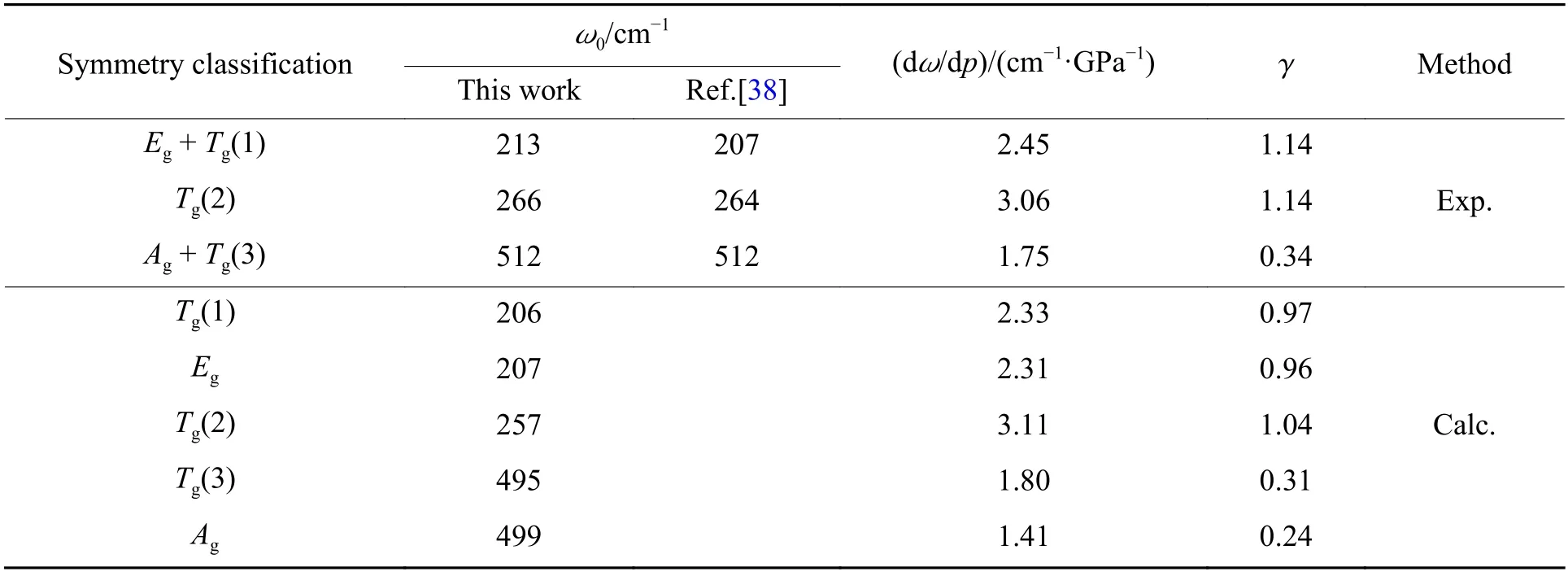
表 1 黄铁矿结构CuS2 的拉曼频率随压力变化及格临爱森参数(γ)Table 1 Pressure dependences of Raman modes and the Grüneisen parameters (γ) of pyrite-type CuS2

群论分析结果表明，黄铁矿结构CuS2振动模式的不可约表示为Γ = Ag+ Eg+ 3Tg+ 2Au+ 2Eu+6Tu。其中Ag+ Eg+ 3Tg为5 个拉曼活性模，Ag为完全对称模，Eg为二重简并模，Tg为三重简并模。Ag和Tg（2）分别对应S—S 原子对同向和反向伸缩振动，Eg摆动模反映S 原子在垂直于S—S 键轴方向的位移，Tg（1）和Tg（3）则对应伸缩模和摆动模的多种组合[39-40]。利用第一性原理计算黄铁矿结构CuS2的声子谱，得到5 个拉曼峰，它们的常压振动频率也在表1 中列出。可以清楚地发现，Tg（1）与Eg以及Tg（3）与Ag之间的波数差在5 cm-1以内，使得在非偏振拉曼光谱中难以分辨[39-40]，导致本次实验和Anastassakis 等[38]的拉曼光谱实验中仅观测到Tg（1）+ Eg、Tg（2）和Tg（3）+ Ag共3 组拉曼峰。此外，本研究的实验值和计算值以及Anastassakis 等[38]的实验结果三者高度吻合，准确地描述了黄铁矿结构CuS2的常压拉曼振动特征。

2.2 黄铁矿结构CuS2 常温高压拉曼光谱

黄铁矿结构CuS2由常压加压到33.0 GPa，并随后卸压至常压过程的拉曼光谱变化特征如图3 所示。图3（a）中，随着压力增加，3 个拉曼峰均向高频方向连续移动，至33.0 GPa 没有拉曼峰增加或消失；卸压过程（图3（b））则保持与加压过程可逆的变化特征。该现象表明，高压仅使CuS2晶体结构致密化，S—S 键和Cu—S 键压缩引起的振动频率增大，没有导致结构相变，反映黄铁矿结构CuS2在0～33.0 GPa压力范围内具有结构稳定性。

图4 展示了拉曼光谱实验测得的3 组CuS2拉曼模Tg（1）+ Eg、Tg（2）、Tg（3）+ Ag和第一性原理理论计算得到的5 个拉曼模Eg、Tg（1）、Tg（2）、Tg（3）、Ag的频率随压力的变化关系。可以看出，拉曼实验值与理论计算值在对应压力下非常接近，两者的最大频率相差小于4%，反映理论计算能很好地描述实验结果。拉曼实验和理论计算数据显示，所有拉曼模的振动频率随压力升高呈线性增加，对拉曼模分别进行线性拟合，拟合给出的频率随压力变化（dω/dp）在表1 中列出，实验和拟合计算结果一致。理论计算数据的拟合结果显示，Eg和Tg（1）模的频率变化速率（dω/dp）非常接近，且常压频率相近，对应拉曼光谱中始终难以分离的情况。而Ag和Tg（3）的频率变化速率略有差异，但Ag模的强度远大于Tg（3）模，在拉曼光谱中基本表现为Ag模信号。

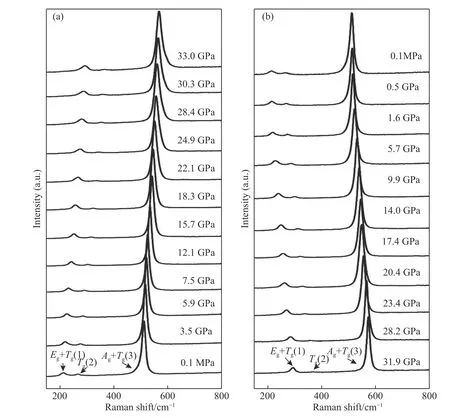
图 3 CuS2 常温加压（a）、卸压（b）过程的代表性拉曼光谱Fig. 3 Representative Raman spectra of CuS2 in the process of increasing pressure (a) and releasing pressure (b)

图 4 实验和理论计算CuS2 的拉曼频率随压力变化关系（黑色圆形和菱形分别对应Exp4 合成的CuS2 在常温加压和卸压过程的结果，三角形表示Exp2 合成CuS2 卸压过程的数据，星形为理论计算值，实线和虚线分别为实验和计算数据线性拟合结果）Fig. 4 Experimental and theory calculated pressure dependence of Raman vibrational modes of CuS2（Black spheres and diamonds correspond to the results of compression process and decompression process of CuS2 synthesised at Exp4，respectively. Black triangles are data of decompression process of CuS2 synthesised at Exp2. The stars represent theory calculated points.Solid line and dotted line are linnear fitted with all experimental and calculated data, respectively.）

2.3 黄铁矿结构CuS2 常温高压X 射线衍射

图5 所示为6.2 GPa 压力下（Exp1 温度处理后）产物的同步辐射X 射线衍射谱，黑色圆形、红色实线和黑色实线分别对应观测值、计算值和误差曲线，在图中以相同比例显示，衍射谱下方黑色垂直短棒为计算CuS2（Pa3）和KCl（Pm3m）的衍射峰位。除去传压介质KCl（B2）相的衍射峰外，剩余的衍射峰可以指标化为Pa3 结构。随后选择KCl（Pm3m）和CuS2（Pa3）作为初始结构模型，利用GSAS-II 软件对衍射谱进行结构精修。精修结果如图5 所示，可见实验和计算结果的X 射线衍射谱吻合较好，误差因子Rp= 1.65%、Rwp=2.85%。因此，确定本次高温高压实验中合成了黄铁矿结构CuS2（Pa3），与拉曼光谱测试结果一致。通过结构精修，得到黄铁矿结构CuS2在6.2 GPa压力下的晶胞参数a = 5.657 3（6）Å，其中原子占位情况为Cu（0，0，0）、S（0.397 4，0.397 4，0.397 4）。

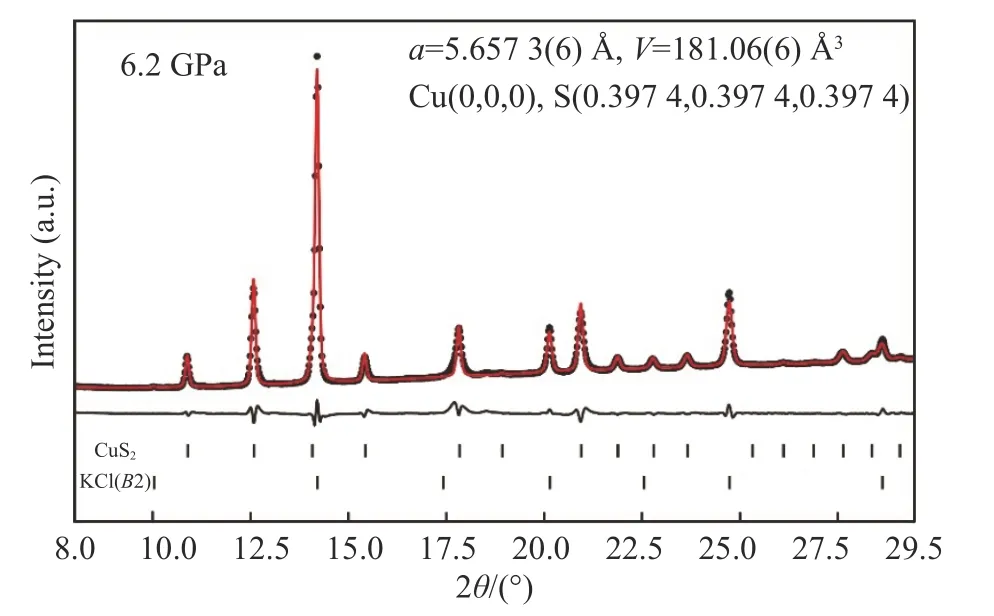
图 5 6.2 GPa 压力X 射线粉末衍射谱Rietveld 结构精修结果Fig. 5 Rietveld refinement analyses of the powder XRD pattern at 6.2 GPa

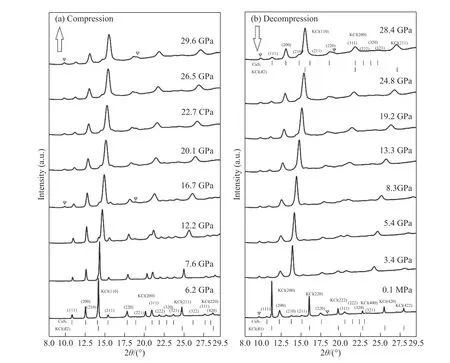
图 6 在加压（a）和卸压（b）过程中CuS2 在不同压力下的X 射线衍射图谱（下三角指示产物中的杂质峰，黄铁矿结构CuS2 和传压介质KCl 的衍射峰位在图中用短棒标出）Fig. 6 X-ray powder diffraction patterns at different pressures on compression (a) and decompression (b)（The inverted triangles indicate impurity peaks. The diffraction peaks of pyrite structure CuS2 and pressure transmitting medium KCl are represented with vertical bars.）

图6 展示了CuS2由6.2 GPa 加压至29.6 GPa，随后卸至常压过程中的代表性X 射线衍射谱。随着压力增加，传压介质KCl 和产物CuS2的衍射峰均逐渐宽化，反映了非静水压力效应及其导致的样品结晶度降低。然而，直到达到最高压力29.6 GPa，仍可以辨识出黄铁矿结构CuS2的（111）、（200）、（210）、（211）、（220）、（222）、（320）、（321）等衍射峰，表明CuS2依然保持黄铁矿结构。卸压至常压过程中，CuS2的衍射峰仍保持宽状态直到常压，没有再次显现出类似6.2 GPa 激光加热后的尖锐峰形，所以压力对样品结晶度变差的影响是不可恢复的。此外，16.7 GPa 时开始出现两个杂峰（图6中下三角指示），但它们与其他衍射峰之间无明确几何关系，不能指认为同一种结构。因此，两个杂峰可能对应于激光高温下可能产生的其他铜硫化合物（如CuS 等）杂质。黄铁矿结构CuS2在低于29.6 GPa压力范围内X 射线衍射谱的变化特征说明其在低于30.0 GPa 压力范围内具有结构稳定性，不发生结构相变，与上述拉曼实验结果保持一致，与Hupen 等[27]发现的结构相变结论不同。

2.4 体积-压力状态方程和格临爱森参数

同步辐射X 射线衍射实验和第一性原理理论计算得到的黄铁矿结构CuS2的晶胞体积随压力变化关系如图7 所示。实验和计算得到的晶胞体积在对应压力下非常接近，对应压力最大体积差小于2%。运用Birch-Murnaghan 状态方程分别对衍射实验数据和理论计算数据进行拟合。将压力导数K0′均固定为4，拟合得到黄铁矿结构CuS2零压晶胞体积V0和体积模量K0分别为：V0（Exp.）= 193.8（5） Å3，K0（Exp.）= 99（2） GPa，V0（Calc.）= 196.5（2） Å3，K0（Calc.）= 85.6（7） GPa。而Hupen 等[27]通过CuS2高压衍射实验给出黄铁矿结构CuS2的状态方程参数为V0（Hupen）=194.1（2） Å3、K0（Hupen）= 98.8（6） GPa 且K0' =4（固定）。所有状态方程参数在表2 中列出。可以看出，本次实验所得零压体积和体积模量值与Hupen 等[27]给出的结果基本一致，而第一性原理理论计算值与两个衍射实验值之间有少许差异。此外，依据格临爱森参数计算公式

图 7 理论计算和衍射实验的CuS2 及其它过渡金属二硫化物MS2（M = Mn，Fe，Co，Ni，Cu）的体积-压力变化关系（黑色圆形和黑色三角形分别对应X 射线衍射实验和第一性原理理论计算结果。黑色实线和黑色虚线是对实验和计算数据进行Birch-Murnaghan 状态方程拟合结果。蓝色、绿色、紫色、棕色和红色实线分别为文献给出的黄铁矿结构MnS2、FeS2、CoS2、NiS2 和CuS2 状态方程结果。）Fig. 7 Pressure-volume relationship of experimental and calculated CuS2 and other transition metal disulfides MS2(M =Mn，Fe，Co，Ni，Cu) (The black circles and triangles represent the experimental and observed data of the CuS2, respectively.The solid black line and dotted black line are the Birch-Murnaghan equation of state fit respectively with listed parameters. The blue, green, purple, yellow, and red line shows the equation of state of the pyrite structure MnS2, FeS2, CoS2, NiS2,and CuS2 in references.)

式中：ω 和ω0分别为各拉曼模在高压和常压的波数；p 为压力；dω/dp 为各拉曼模频率随压力的变化；K0选择本研究中状态方程拟合结果K0（Exp.）=99（2） GPa 和K0（Calc.）= 85.6（7） GPa。计算得到的各振动模的格临爱森参数值（γ）在表1 中给出。

作为对比，一些黄铁矿结构二硫化物MS2（M = Mn，Fe，Co，Ni）的体积随压力变化曲线也在图7中给出，它们的状态方程参数[14,27,41-43]列于表2 中。对应压力下，5 种黄铁矿结构二硫化物的体积大小关系为VFe＜ VCo＜ VNi＜ VCu＜ VMn，与King 等[23]给出的M—S 键长序列LFe—S＜ LCo—S＜ LNi—S＜ LCu—S＜LMn—S一致。5 种物质的体积模量中，FeS2的体积模量最大，MnS2的体积模量最小，而CoS2、NiS2和CuS2的体积模量之间相差不大。体积模量大小同样与M—S 键长关系密切，往往M—S 键长越长体积模量越小，则压缩性越强。说明在黄铁矿结构二硫化物MS2（M = Mn，Fe，Co，Ni）中，MS6配位八面体（M—S 键长）主导着晶胞体积大小和晶体压缩性，S—S 键长的影响较小，而S—S 键对拉曼振动频率影响更大。根据CuS2与其他黄铁矿结构二硫化物之间的相似性推测，Cu 与其他二硫化物中过渡金属阳离子（Mn2+，Fe2+等）类似，以+2 价形式存在。

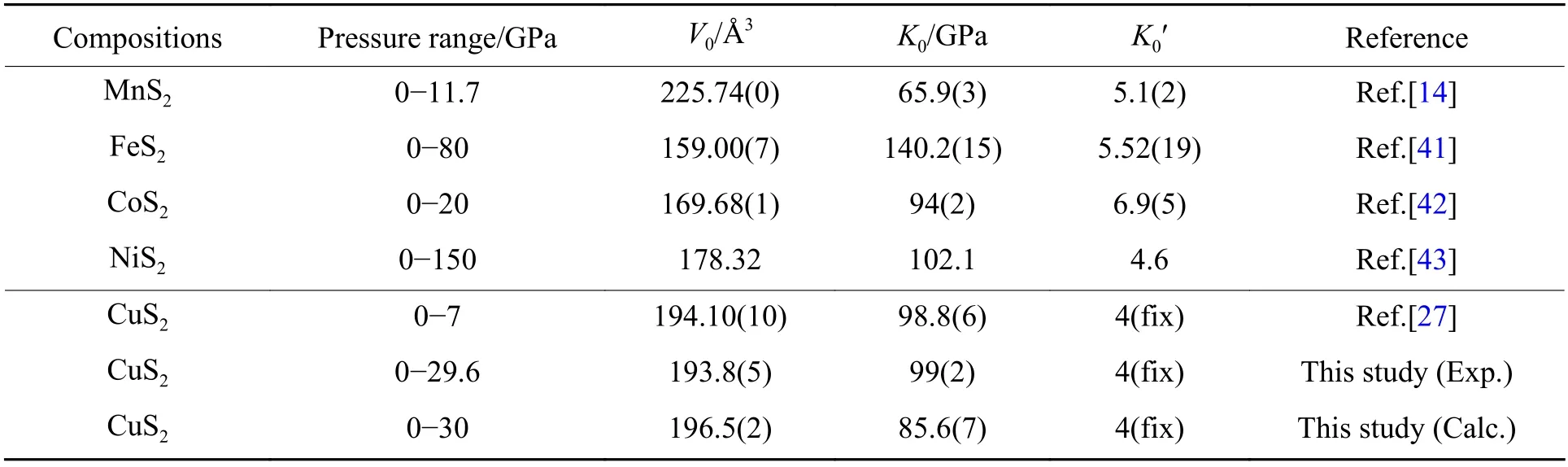
表 2 黄铁矿结构CuS2 与其他黄铁矿结构过渡金属二硫化物的零压体积模量和晶胞体积对比Table 2 Comparison of zero-pressure bulk modulus (K0) and unit formula volume (V0) of CuS2 with that of other pyrite structure transition-metal disulfides

3 结 论

利用金刚石压腔在不同温压条件下合成了黄铁矿结构CuS2，拓展了已知的CuS2热力学稳定区间。通过显微拉曼光谱和高压同步辐射X 射线衍射实验并结合第一性原理理论计算，发现了CuS2在低于30.0 GPa 压力范围内保持结构稳定，不发生结构相变，与已知的Hupen 等[27]所给结论不同。拉曼光谱研究表明，CuS2所有拉曼模均随压力呈连续单调线性变化，并给出了各个模的线性关系。利用Birch-Murnaghan 状态方程对同步辐射X 射线衍射实验和第一性原理计算得到的晶胞体积随压力变化数据进行拟合得到，V0（Exp.）= 193.8（5） Å3，K0（Exp.）= 99（2） GPa，V0（Calc.）= 196.5（2） Å3，K0（Calc.）=85.6（7） GPa，K0′均固定为4，与Hupen 等[27]研究给出的黄铁矿结构CuS2状态方程参数基本吻合。通过和其他黄铁矿结构二硫化物MS2（M = Mn，Fe，Co，Ni）对比发现，MS6配位八面体大小（M—S 键长）主导着晶胞体积大小和晶体压缩性。它们之间的一致性变化规律似乎指示黄铁矿结构CuS2中的Cu 为+2 价。黄铁矿结构CuS2的高温高压稳定性对于认识Cu 在地球深部环境中的价态和赋存形式具有重要指示意义。