平场数据采集间隔对莱曼阿尔法太阳望远镜平场精度的影响分析∗

李敬伟 黎 辉 封 莉 李 瑛 黄 宇赵 洁 卢 磊 应蓓丽 薛建朝 杨雨桐

(1中国科学院紫金山天文台暗物质与空间天文重点实验室南京210023)

(2中国科学技术大学天文与空间科学学院合肥230026)

1 背景介绍

莱曼阿尔法太阳望远镜(LST)[1–3]是先进天基太阳天文台(ASO-S)[4–5]卫星的3个有效载荷之一,它由白光太阳望远镜(WST)、全日面成像仪(SDI)、日冕仪(SCI)和导星镜(GT)组成[2,6].SDI和WST的视场为1.2倍太阳半径,SDI的工作波段为莱曼阿尔法波段(121.6±7.5nm),WST的工作波段为紫外窄带连续谱(360±2.0nm)[2,6].

平场是电荷耦合器件(CCD)和互补金属氧化物半导体(CMOS)等数值化半导体探测器像元对入射光响应的非均匀性的表征,实际的观测图像需要通过平场对探测器响应的非均匀性进行改正,才能获得真实的观测图像.通常可以通过对均匀光源成像或稳定光源在不同曝光时间下的图像进行拟合得出.但有时候,这两种光源都难以获得,在1991年Kuhn,Lin和Loranz提出了一种利用相对稳定非均匀图像获取平场的方法[7],在2004年Chae[8]在此基础上进行了一定的改进,将太阳图像、光强变化以及平场等参数自由化,Kuhn等[7]和Chae[8]都采用的是太阳像在探测器不同位置获得图像的方法来获得平场,我们简称该方法为KLL方法.该方法使用观测的太阳像本身作为光源,改变望远镜指向获得多张位于探测器不同位置的太阳像,通过迭代方法计算平场[7–8].目前,地基全日面太阳望远镜,如光学和近红外太阳爆发探测望远镜(ONSET)[9],大熊湖太阳天文台的Hα全日面太阳望远镜[10],天基全日面太阳观测载荷,如太阳动力学观测卫星(SDO)搭载的太阳大气成像仪(AIA)[11–12]及日震和磁成像仪(HMI)[13]均采用KLL方法获取平场.而局部视场的太阳望远镜如太阳界面层成像光谱仪(IRIS)和大熊湖太阳天文台的磁场观测亦采用了该方法[14–15].

在ASO-S卫星发射后,通过卫星指向偏离卫星-日心连线方向,得到不同指向的多幅全日面图像,并利用获得的非均匀但相对稳定的全日面图像,使用KLL方法通过最小二乘法拟合迭代得到SDI和WST所需的平场图像[6].

卫星调姿到指定位置并保持稳定需要一定的时间,同时图像采集也需要时间,因此,相邻两个位置的图像采集有一定的时间差.由于太阳像或多或少存在变化[16–18],这一时间差的长短将直接影响所得的平场精度.而且平场定标精度也取决于全日面图像的相对稳定性、完成全部位置图像的采集时间以及算法的优化等因素.全日面太阳图像在此过程中变化越少,采集图像的总时间越短,则定标精度通常就越高.根据SDO卫星AIA技术文档所示的极紫外波段平场的情况来看,KLL方法在极紫外波段平场定标精度不是很高,这对于莱曼阿尔法太阳望远镜来说也具有一定的参考价值.

在本文中我们将利用HMI和AIA的观测数据来测试使用KLL方法得到的平场定标精度对相邻位置时间间隔的敏感性.

文章的结构安排如下:我们在第2节介绍计算平场时的观测数据来源,平移平场数据日心位置的要求及生成的平移平场数据的情况等内容;在第3节介绍使用KLL方法对这些数据的处理和计算以及对所得平场的分析;在第4节对结果进行讨论并给出结论.

2 数据及处理

2.1 数据位置要求

考虑到WST和SDI的视场均为1.2倍太阳半径的圆形视场,而探测器的读出图像通常为方形.为了得到全视场的平场,我们拟让卫星平台指向13个(只考虑1.2倍太阳半径的内切圆平场)或21个(同时考虑探测器4个角区域的平场)不同的位置(其中1个为参考位置),探测系统在这些位置分别进行太阳像的图像采集.

在日心坐标系中,我们将参考图像的太阳像中心坐标设为(0,0).分析得到在进行太阳平场数据观测时21个位置点的日心坐标分别为(单位为角分(′)):(0,0)、(4.8,0.0)、(4.157,2.4)、(2.4,4.157)、(0.0,4.8)、(−2.4,4.157)、(−4.157,2.4)、(−4.8,0.0)、(−4.157,−2.4)、(−2.4,−4.157)、(0.0,−4.8)、(2.4,−4.157)、(4.157,−2.4)、(11.085,6.4)、(6.4,11.085)、(−6.4,11.085)、(−11.085,6.4)、(−11.085,−6.4)、(−6.4,−11.085)、(6.4,−11.085)、(11.085,−6.4),各个位置点在探测器上的分布如图1所示.在下面使用KLL方法计算平场时,我们均采用了上述的21个平移平场位置进行计算.

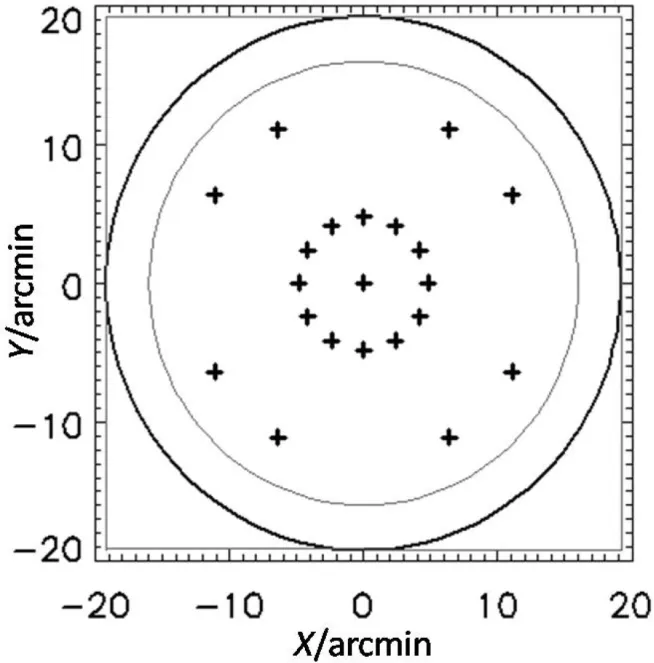
图1 拟采用的21个平移位置相对于日面中心的坐标示意图,其中中间的21个加号是各个平移图像的日心位置,中间的小圆圈代表中心点位置的日面边缘,大圆圈代表WST和SDI探测器视场,方框代表WST和SDI探测器的整个靶面.Fig.1 The relative coordinates of the 21 of fset positions relative to the coordinates of the disk center of Sun.The 21 pluses(+)in the middle of the plot indicate the disk center of the Sun of each of fset images.The small circle represents the limb of the Sun at the central position,the big circle represents the field of view(FOV)of WST and SDI,and the box stands for the whole area of the WST and SDI detectors.

2.2 测试数据与方法

基于观测数据的相似性,我们将使用HMI/SDO的6174˚A的白光观测数据作为WST KLL方法平场的测试数据,使用AIA/SDO的304˚A和1700˚A观测数据作为SDI KLL方法平场的测试数据.我们选用一定相邻位置时间间隔的观测数据,按照上述21个位置点进行数据平移,生成所需要的平场计算数据,然后使用KLL方法的程序进行平场计算,最后我们将所得到的平场进行分析.

选用HMI 6174˚A白光观测数据作为WST的计算数据是因其与WST的3600˚A窄带连续谱观测得到的图像几乎相同.而选用AIA 304˚A和1700˚A成像观测数据作为SDI的计算数据则是考虑到1700˚A成像观测计数预期高于SDI计数,而304˚A成像观测计数预期低于SDI的计数,因此根据经验预期得到的SDI平场数据会较304˚A的更优,而稍差于1700˚A的平场.

WST计算数据的来源及相邻位置时间间隔:我们使用了2013年10月24日和2017年4月9日2d的HMI的白光观测数据,计算时使用的相邻位置时间间隔分别为45s、90s、135s、180s、225s、270s、315s、360s、540s和720s,每天10组数据,共20组数据,每组21幅图像.

SDI计算数据的来源及时间间隔如下:第1种计算数据我们使用了2013年10月17日和2017年4月8日2d的AIA 304˚A的观测数据,计算时选用的相邻位置时间间隔分别为48s、96s、144s、192s、240s、288s、336s、384s、480s和720s,每天10组数据,共20组数据,每组21幅图像;第2种计算数据我们使用了2012年1月11日,2013年10月24日和2017年4月9日3d的AIA 1700˚A的成像观测数据,计算时选用的相邻位置时间间隔分别为48s、96s、144s、240s、288s、336s、384s、480s和720s等,每天10组数据,共30组数据,每组21幅图像.

需要注意的是,计算时选用的相邻位置时间间隔受到数据源的观测时间的限制,例如HMI观测数据的最短时间间隔为45s,在生成WST平场计算数据时我们选择使用的最短相邻位置时间间隔为45s,AIA 304˚A观测数据的最短时间间隔为12s,而AIA 1700˚A观测数据的最短时间间隔为24s,在生成SDI平场计算数据时,我们选择使用的最短相邻位置时间间隔为48s,计算时选用的前8个时间间隔是最短时间间隔的n倍(n=1,2,3,4,5,6,7,8),而最后两个相邻位置时间间隔一个为9min(或8min),另一个为12min.最长相邻位置时间间隔选用12min的依据是AIA在做平场数据观测时,相邻位置时间间隔为10min左右,所以我们在计算时选取的最长相邻位置时间间隔为12min.

计算数据分别选取2012年、2013年和2017年的原因是其分别位于第24太阳活动周的太阳极大年和太阳极小年附近,而太阳活动的强弱可能会对使用KLL方法计算的平场定标精度造成一定的影响,所以我们分别选取了这3个年份的观测数据作为计算数据源,其中2012年的观测数据只选用了AIA 1700˚A的数据.

2.3 计算数据的生成

根据上面提到的21个位置的日心坐标,将HMI和AIA的观测数据按要求生成WST和SDI的平场计算数据,总共70组计算数据,我们在图2中仅展示生成后的一组WST相邻位置时间间隔为45s的平场计算数据,其余各组平场计算数据与此类似,不再展示.

我们在使用KLL方法计算平场时,分为理想和观测两种情况进行计算:第1种为理想情况,即计算数据的平场是理想平场(理想情况下的平场数据的数值均为1.0),然后使用KLL方法计算平场,此种情况下得到的平场代表了KLL方法的最佳平场定标精度极限情况;第2种为观测情况,利用HMI和AIA发布的由观测得到的平场数据(如图3所示)将经过平场改正后的数据还原为改正前的观测数据,然后用KLL方法计算平场,此种情况下得到的平场反映了KLL方法在实际观测情况下的平场定标精度.

3 平场的计算与分析

我们使用上述的70组计算数据,使用KLL方法将每组计算数据按照上述理想和观测两种情况进行计算,共得到140个平场.

我们在计算平场过程中遇到如下困难:(1)第1种SDI计算数据的计数较低且在日面边缘存在冕环、日珥、针状物等现象的干扰;(2)第2种SDI计算数据计数相对较高,但是由于其原始平场的影响,使得生成的图像中有时会出现较大起伏,导致在使用索贝尔函数计算日心坐标和太阳半径时经常出现误判现象.而WST的平场计算数据则不存在这些问题.为了克服这些困难,我们将图像进行一定阈值(采用阈值的目的是为了消除日面亮度的起伏对判断程序的干扰,我们采用对计算图像限制其最大值和最小值的阈值方法,屏蔽掉日面对程序的干扰而提高了程序对日面边缘梯度的判断,所采用的阈值大小需要根据数据的实际情况设定)处理和/或去除冕环、日珥等影响后,再使用索贝尔函数计算得到日心坐标和太阳半径等参数,最后将得到的日心坐标和太阳半径等参数作为输入参数,使用KLL方法计算平场.

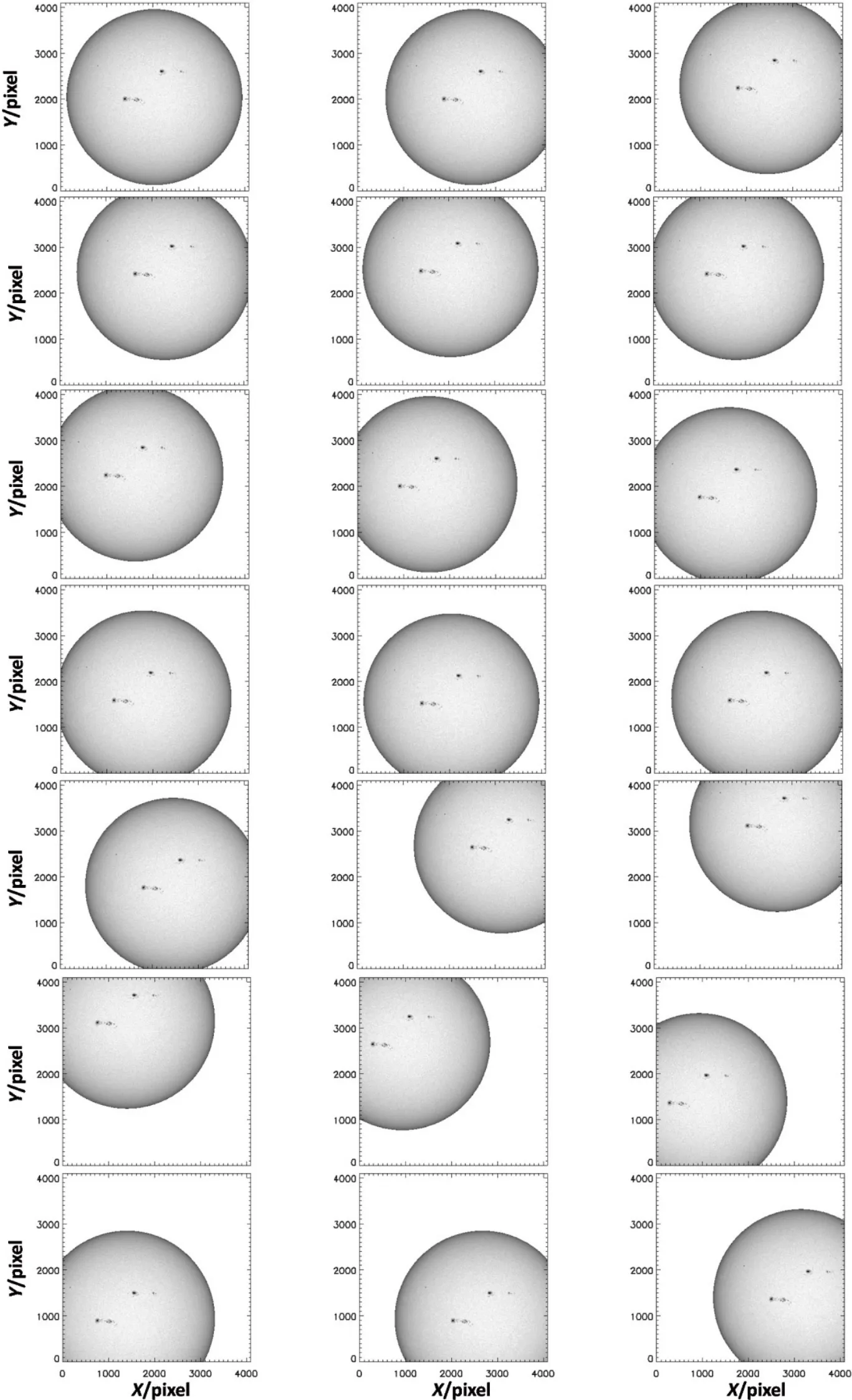
图2 由HMI强度图像生成的相邻位置时间间隔为45 s的21个位置的WST平场数据示意图Fig.2 Generated 21 of fset images for the WST flat field data from HMI intensity images with a time interval of 45 s

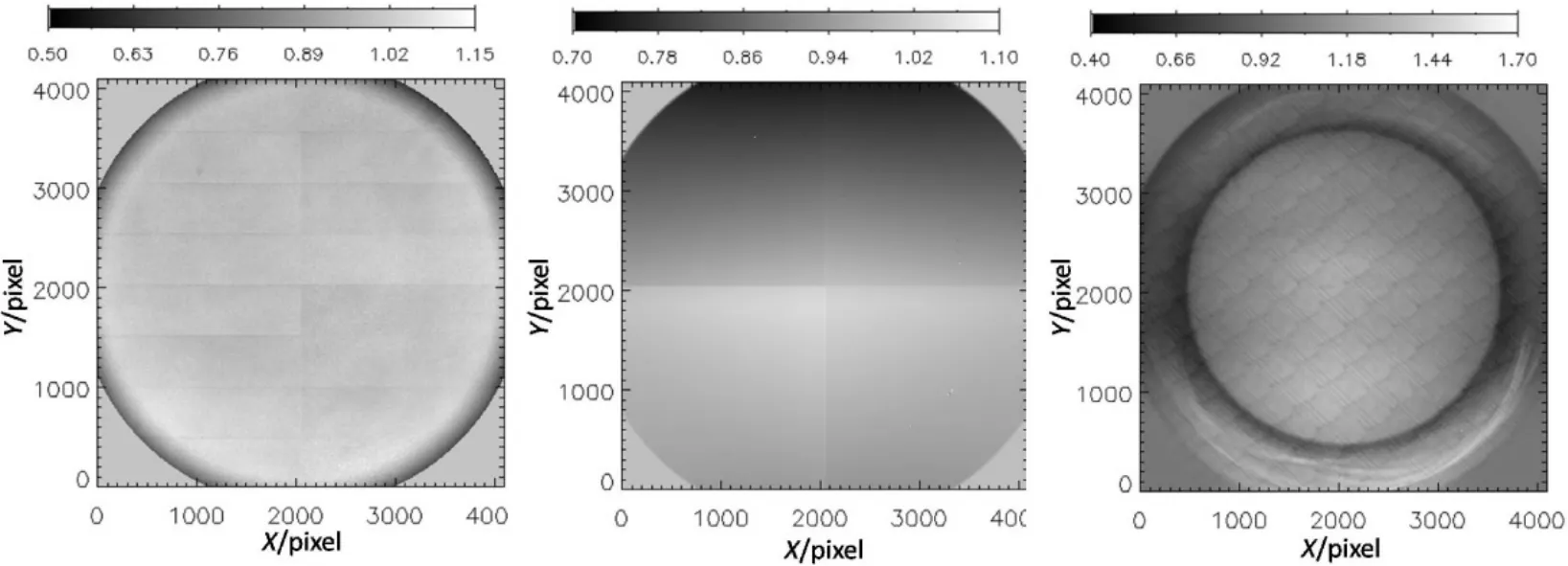
图3 用于还原观测图像的HMI(左)、AIA 304˚A(中)和1700˚A(右)的平场图像.需要注意的是图中平场数据显示的范围由其上的灰度棒给出.Fig.3 Flat field images used to restore the observation images:HMI(left),AIA 304˚A(middle)and 1700˚A(right)flat field images.Note that the range of the flat field data in the figure is given by the scale bar.

经过计算我们得到WST和SDI共140幅平场图像,我们这里只给出了WST和SDI的平场示意图,如图4和图5所示.图4是按理想情况计算得到的平场,图5是按观测情况计算得到的平场.

图4 按理想情况由HM I强度图像计算得到的WST平场图像(左)和由AIA 304˚A(中)及1700˚A(右)图像得到的SDI平场图像.需要注意的是图中平场数据显示的范围由其上的灰度棒给出.Fig.4 Derived WST flat field image with the ideal flat field assumption from HMI intensity images(left),and the SDI flat field images from AIA 304˚A(middle)and 1700˚A(right)images.Note that the range of the flat field data in the figure is given by the scale bar.

下面我们将得到的WST和SDI的平场进行统计分析.我们得到的WST和SDI的平场是以位于探测器中心的参考太阳日面边缘的外接正方形进行归一化处理的,而如图3所示,原始平场的4个边角区域均为1,因此在统计分析时,排除所得平场的4个边角区域.统计区域类似于图4和图5排除4个边角区域的圆形视场,这里不做逐一说明.

我们的统计方法分为两种方法:

统计方法一:对于上述第1种(理想)情况得到的WST和SDI的平场,直接统计平场的最大值、最小值、均值、标准偏差(σ)值以及平场值在均值±1σ之内,均值±3σ之内和1.0±2%之内的像元数占总像元数的比例;统计方法二:对于上述第2种(观测)情况得到的WST和SDI的平场,首先将得到的平场与其相应的原始平场相除,再进行与方法一同样的统计.

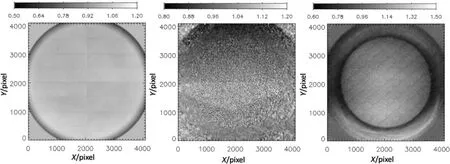
图5 按观测情况由HM I强度图像计算得到的WST平场图像(左)和由AIA 304˚A(中)及1700˚A(右)图像得到的SDI平场图像.需要注意的是图中平场数据显示的范围由其上的灰度棒给出.Fig.5 Derived WST flat field image with the observation images from HMI intensity images(left),and the SDI flat field images from AIA 304˚A(middle)and 1700˚A(right)images.Note that the range of the flat field data in the figure is given by the scale bar.

经过统计分析,我们总共得到了14个统计表格.我们发现在上面的统计参数中,如果用σ值作为平场定标精度的衡量标准,则σ值越小说明平场数值越集中于均值附近,σ值越大则说明平场数值对均值的分散程度变大.因此得出σ值可以很好地衡量所得WST和SDI平场的质量,将同一天10个平场的σ值与其相应的相邻位置时间间隔显示在一起,则可以反映出平场定标精度与相邻位置时间间隔之间的变化趋势.我们在图6–8中给出了理想和观测两种情况下所得的WST和SDI平场的σ值随相邻位置时间间隔的变化曲线.

我们在计算平场时,使用的KLL方法是在可视化交互数据语言(IDL)中实现的.一组21张4096×4096像素图像数据,在所用计算机配备1.80 GHz处理器,64位操作系统和计算时选取2×2像素合并的情况下,迭代10次的计算时间约为270s.

4 讨论与结论

本文中我们通过与LST实际观测类似的HMI的强度图像以及AIA 304˚A和1700˚A图像分别测试LST载荷中WST和SDI用KLL方法获取探测器平场时,相邻两个位置图像获取的时间间隔对所得平场精度的影响.通过分析,我们得到如下结果:

(1)从图6可知,通过HMI强度图像所测试的WST的平场定标精度高,并且随相邻位置时间间隔的变化很小,究其原因是白光图像比较稳定且其自身随时间的变化很缓慢;LST的WST仪器观测图像与其类似,预期使用KLL方法可以得到定标精度很高的平场且几乎不随相邻位置时间间隔的变化而变化;

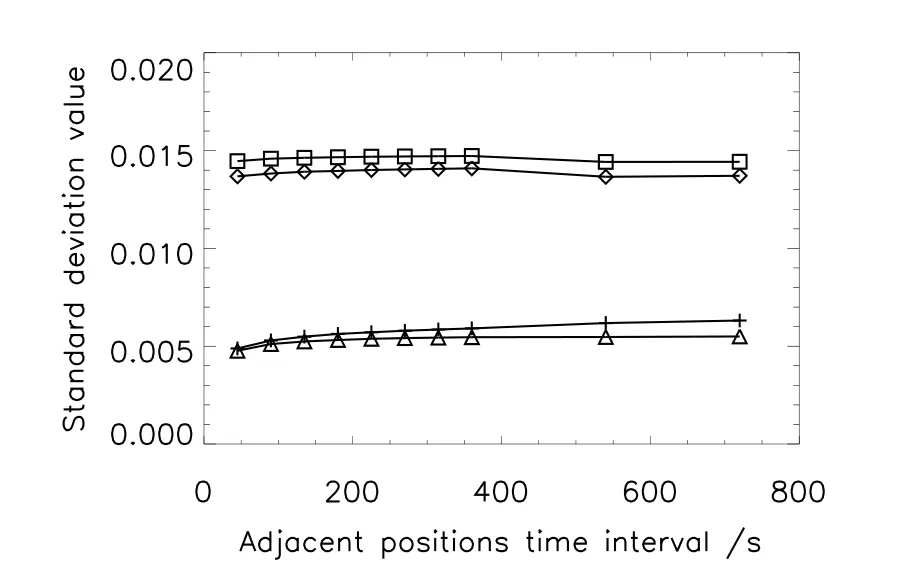
图6 由HM I 2013年(加号和菱形)和2017年(三角形和正方形)数据按理想(加号和三角形)和观测(菱形和正方形)两种情况得到的WST平场的σ值随相邻位置时间间隔的变化.Fig.6 Variation of the standard deviations(σ)of the derived WST flat field with time interval respectively under the ideal flat field assumption(plus and triangle)and observation images(diamond and square)from HMI data obtained in 2013(plus and diamond)and 2017(triangle and square).

(2)从图7可知,通过AIA 304˚A波段图像所测试的SDI的平场定标精度一般,并且随相邻位置时间间隔的增加变差,特别是在相邻位置时间间隔大于240s后,变化愈加明显,且在小于240s时存在一定的起伏.该波段平场定标精度的明显变化与该波段图像上结构较多、数据计数较低(信噪比小)且随时间变化相对较快有关.计算表明,SDI的图像信噪比会明显高于AIA 304˚A波段,因此预期LST的SDI定标精度优于该波段的定标精度;

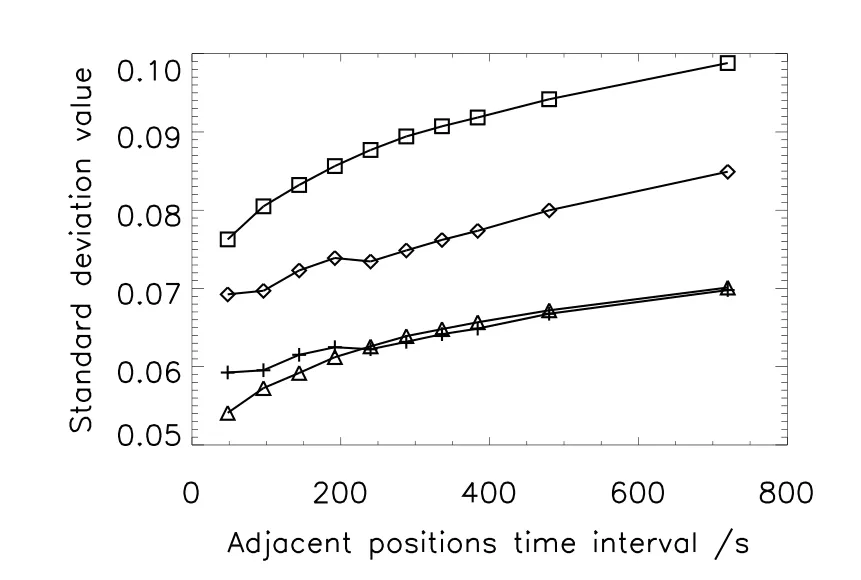
图7 由AIA 304˚A 2013年(加号和菱形)和2017年(三角形和正方形)数据按理想(加号和三角形)和观测(菱形和正方形)两种情况得到的SDI平场的σ值随相邻位置时间间隔的变化.Fig.7 Variation of theσof the derived SDI flat field with time interval resp ectively under the ideal flat field assumption(plus and triangle)and observation images(diamond and square)with AIA 304˚A data obtained in 2013(plus and diamond)and 2017(triangle and square).

(3)从图8可知,通过AIA 1700˚A波段图像所测试的SDI定标精度相对较好,并且随相邻位置时间间隔的增加也有明显的变化,但其变化明显优于304˚A波段而差于白光波段,原因是该波段图像的结构和信噪比均在AIA 304˚A波段和HMI强度图像之间.对于该波段模拟数据得到的平场定标精度而言,在相邻位置时间间隔大于240s后,平场定标精度变差的趋势相对更加明显;

(4)从图6可以看出,对于WST平场来说,其在太阳活动周的极大年和极小年附近相差不大,说明随着太阳活动周的变化对其平场定标精度来说影响很小;而图7和图8则说明,对于SDI平场来说,在太阳活动周极小年附近,定标精度相对较好,说明太阳活动的多少对其定标精度有一定的影响.

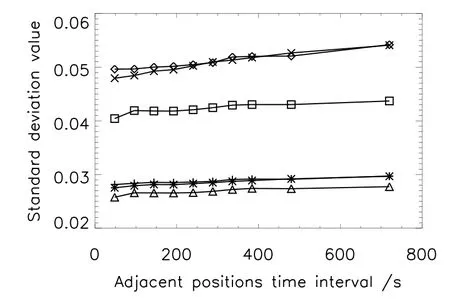
图8 由AIA 1700˚A 2012年(星号和交叉号),2013年(加号和菱形)和2017年(三角形和正方形)数据按理想(加号,三角形和星号)和观测(菱形,正方形和交叉号)两种情况得到的SDI平场的σ值随相邻位置时间间隔的变化.Fig.8 Variation of theσof the derived SDI flat field with time interval resp ectively under the ideal flat field assumption(plus,triangle and asterisk)and observation images(diamond,square and cross)with AIA 1700˚A data obtained in 2012(asterisk and cross),2013(plus and diamond),and 2017(triangle and square).

综合上面的分析,我们得到如下结论:在使用KLL方法获取平场定标数据时,相邻位置的图像采集时间间隔越短越好.具体到LST来说,在获取采用KLL方法进行WST和SDI平场定标数据时,考虑卫星平台进行姿态调整和图像采集的时间,WST平场精度对相邻位置采样时间间隔不敏感,而SDI时间间隔需要在240s范围内.这对卫星平台的姿态调整到稳定所需的时间给出了一定限制.

需要指出的是,以上基于HMI和AIA观测数据进行计算所得的结果对于LST的平场定标精度对相邻位置时间间隔的敏感性具有一定的参考价值.但LST的WST和SDI观测数据本身与HMI的和AIA 304˚A及1700˚A的观测数据存在着一定差异,其平场定标精度与相邻位置时间间隔之间的关系需要等ASO-S卫星发射后,在LST在轨调试期间进行相应的观测及验证.