ASO-S/FM G稳像系统的柔性支撑摆镜设计与仿真∗

陈继喆 章海鹰 郑兆瑛 倪厚坤

(1中国科学院国家天文台南京天文光学技术研究所南京210042)

(2中国科学院天文光学技术重点实验室(南京天文光学技术研究所)南京210042)

(3中国科学院大学北京100049)

(4中国科学院大学天文与空间科学学院北京100049)

1 引言

先进天基太阳天文台(Advanced Space-based Solar Observatory,ASO-S)是一颗计划中的专用太阳观测卫星,将在2021年底或2022年上半年择机发射,届时卫星将在太阳活动峰年进入高度720 km的太阳同步轨道,工作寿命为4 yr[1].

ASO-S卫星包含3个载荷:全日面矢量磁像仪(Full-disk vector MagnetoGraph,FMG)、太阳硬X射线成像仪(Hard X-ray Imager,HXI)、莱曼阿尔法太阳望远镜(Lymanalpha Solar Telescope,LST).作为ASO-S卫星的主载荷之一,FMG载荷分系统将以高时间分辨率、高空间分辨率和高灵敏度开展全日面太阳矢量磁场测量,通过连续稳定的观测,研究太阳磁场的发生、发展、相互作用及其效应,从而深入理解耀斑和日冕物质抛射过程中的能量积累、触发、释放和传输机制,并为空间天气事件预报提供观测基础[2–4].

FMG载荷通过集成稳像系统满足长时间连续稳定观测的指标要求[5],稳像系统主要通过操纵摆镜快速摆动以消除目标图像的抖动,因此摆镜是稳像系统的重要组成部分.摆镜机构的力学情况,尤其是摆镜镜面的变形情况,将对搭载稳像系统的FMG载荷的分辨率与精度造成显著影响.

目前空间载荷摆镜的连接方式可大致分为两种:通过螺栓、压板等机械零件进行的连接以及通过胶体等黏结剂进行的连接.通过螺栓、压板等方式连接的光学器件易受外界振动、力学传递的影响,螺栓预紧力及装配应力也会对摆镜的装配环节造成工艺上的麻烦,引起光学性能下降[6–7].通过胶体等黏结剂连接尽管具备了一些柔性连接的特性,但存在黏结剂固化收缩产生内应力的问题以及在复杂空间环境中长时间使用脱胶的风险[8].

为了规避上述两种连接方式的缺点,借鉴国际上同类科学载荷的成功经验[9–10],兼顾FMG载荷工程要求以及柔性支撑适合承受发射飞行阶段较大振动的特性,本文提出一种利用弹性压片3点侧面柔性支撑的摆镜机构方案.

2 稳像系统组成

FMG载荷的稳像系统由4部分组成:摆镜(Tip/tilt Mirror)、分束棱镜(Beam Splitter)、边缘探测器(Limb Sensor)以及稳像控制器(Control),如图1所示.太阳光进入望远镜后,由斜向放置的摆镜反射至分束棱镜分光,一部分光进入滤光器所在的主光路成像,用于科学观测;另一部分光进入偏差探测光路,成像在边缘探测器上,用于稳像控制.稳像控制器接收摆镜的位置信号和边缘探测器输出信号,驱动摆镜偏转,实时补偿太阳入射角的偏差.

图1 FMG稳像系统示意图Fig.1 Illustration of the FMG image stabilization system

3 摆镜的设计

3.1 摆镜设计指标

FMG稳像控制系统的设计带宽暂定为100 Hz,根据工程实践经验,闭环带宽设计为控制对象谐振频率的1/10,因此摆镜的谐振频率应大于1000 Hz.对日观测时摆镜的摆动行程为±0.1 mrad,同时根据摆镜的光学性能要求以及摆镜在光路中斜向45◦放置的特性,需确保椭圆形通光口径内摆镜静态和动态的面形波峰波谷差(Peak-Valley,PV)<λ/10,面形均方根误差(Root Mean Square,RMS)<λ/40(λ为波长,λ=532.42 nm).

FMG载荷在集成至卫星总体发射之前,还将进行一系列的地面观测试验.因此,除了需要对在轨无重力环境进行仿真,还应保证地面有重力试验环境的面形依然符合要求,进一步探讨重力对面形的影响.

3.2 摆镜设计方案

如图2所示,摆镜机构主要是由支架(Support)、摆镜平台(Tip/tilt Mirror Platform)、摆镜室(Mirror Cell)和平面镜(Plane Mirror)组成.摆镜室通过螺钉固定在摆镜平台上,并在内圈的3等分位置开3个半圆柱形缺口;平面镜的侧面也加工3个圆柱形沟槽,并胶合3个带球头的非金属圆柱体,这种球头圆柱体被称为摆镜支点(Mirror Fulcrum).通过这3个摆镜支点与镜室半圆柱缺口的配合,将平面镜装配到镜室上,实现平面镜的周向定位.在平面镜底面与镜室间设置3组非金属摆镜垫片(Mirror Shim),摆镜垫片底部与摆镜室胶合固定,再通过3组弹性压片(Elastic Presser)压紧球头以及调整垫片高度使摆镜支点略微凸起,得到不同大小的弹性压片支持力,实现柔性的轴向定位.摆镜机构部分结构材料属性如表1所示.

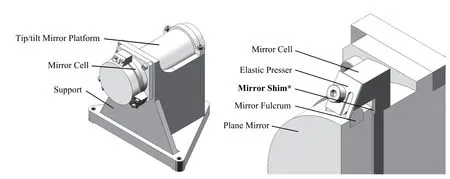
图2 摆镜机构(左);摆镜机构局部剖面视图(*摆镜垫片厚度按需调整)(右).Fig.2 Tip/tilt mirror mechanism(left);local section view of the mechanism(*the thickness of mirror shim can be adjusted on demand)(right).

弹性压片与摆镜支点相接触的模型,可以简化为悬臂梁的弯曲变形模型,其弹性压片接触点的挠度可以用此式计算:

其中,ω为接触点的挠度,F为接触点处提供的支持力,l为接触点到固定支点的距离,E为弹性模量,I为惯性矩.

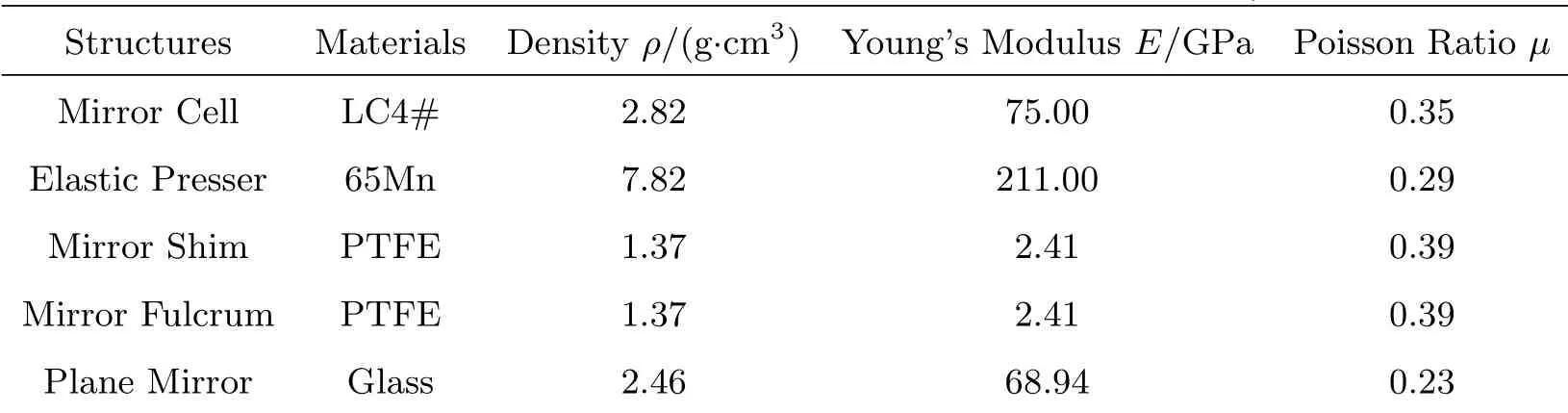
表1 摆镜机构部分结构材料属性Table 1 Pr op erties of som e structure comp onents of the tip/tilt m irror

为了确定合理的垫片厚度范围,根据(1)式求得不同支持力大小下的接触点挠度.因弹性压片变形方向与摆镜垫片存在夹角,垫片厚度的实际增量与接触点挠度使用三角函数进行转换.考虑实际加工工艺,对垫片总厚度取整,确定3种不同支持力的摆镜模型,如表2所示,做进一步仿真计算.

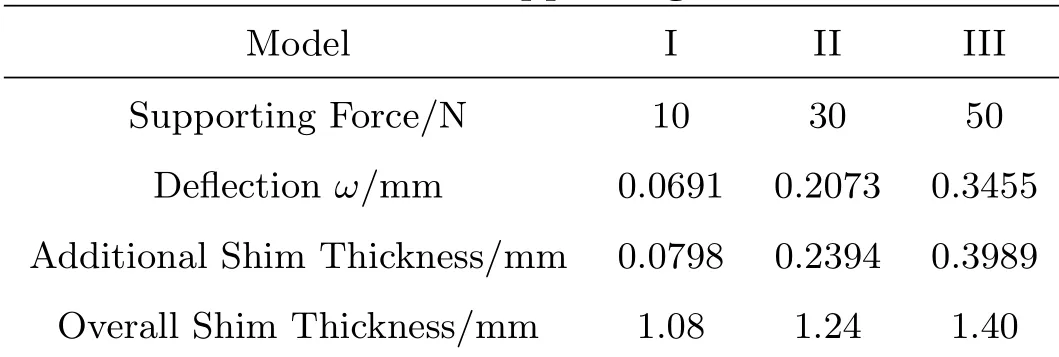
表2 支持力折算摆镜垫片厚度Table 2 Conversion between sup p orting force and shim thickness

4 摆镜的分析

4.1 建立有限元模型

摆镜机构在建模时确定坐标系:X轴指向摆镜光轴方向,Y轴垂直于摆镜光轴,平行于摆镜机构与载荷箱连接底面,Z轴垂直于载荷箱连接底面向上,3者关系符合右手法则.因为仿真的重点是摆镜面形精度,为减小仿真计算规模,故将模型导入有限元软件时仅保留与摆镜平台连接的摆动部分.导入的摆动部分进行网格划分,对平面镜、弹性压片、摆镜支点进行了局部网格细化,网格划分如图3所示.经模态分析,3种摆镜模型的摆动部分谐振频率均远大于1000 Hz.

4.2 静力学仿真

针对在轨无重力环境进行静力学仿真,完成后导出结点位移数据,经后处理得到各个模型的PV值和RMS值,如表3所示.

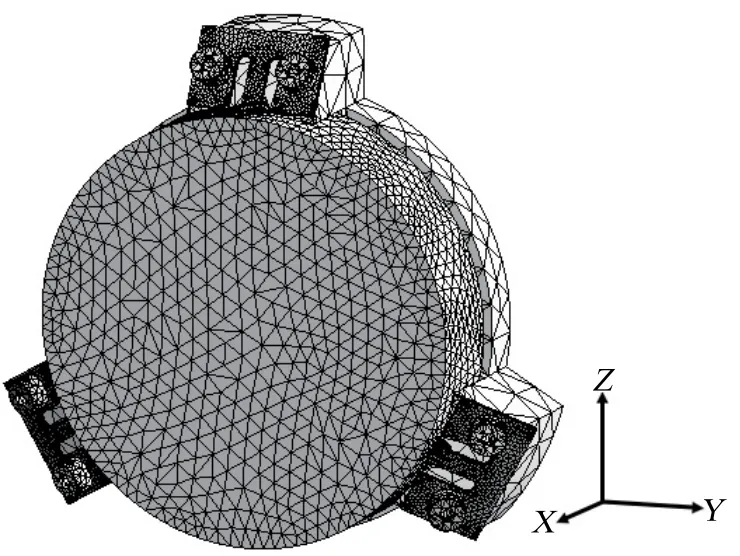
图3 摆镜摆动部分有限元模型Fig.3 Finite element model of the swing part of the tip/tilt mirror

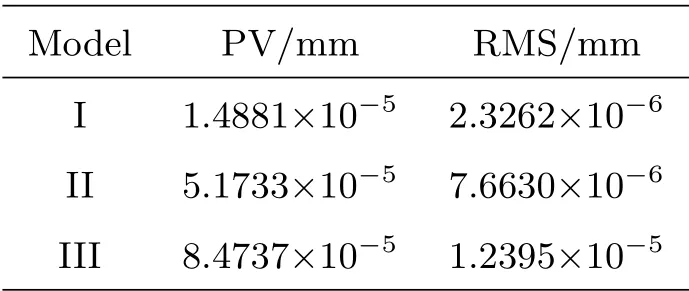
表3 无重力作用静态面形PV、RMS值Table 3 PV and RM S of the static surface und er zero gravity

消除刚体位移的静态面形,如图4所示.

图4 模型I无重力作用静态面形云图(左);模型II无重力作用静态面形云图(中);模型III无重力作用静态面形云图(右).Fig.4 The contour of Model I of static surface under zero gravity(left);the contour of Model II of static surface under zero gravity(middle);the contour of Model III of static surface under zero gravity(right).

摆镜在光路中斜45◦放置,圆形光束在摆镜上呈椭圆形通光口径,通光口径没有占据摆镜全部面积,实际通光口径内静态面形如图5所示.

所有模型的面形精度(PV、RMS值)曲线如图6所示.图中Aperture PV、Aperture RMS指镜面椭圆形通光口径内的面形精度.

分析仿真结果,静态面形精度与压片支持力有关.由表3、图6可以看出,随垫片厚度增加,压片支持力增大,面形精度PV、RMS值也随之增大.即受力越小,平面镜静态面形越好.

同时,由图4–5可以看出,受侧面支撑的影响,平面镜的变形集中在摆镜支点嵌入平面镜的边缘处,但因为通光口径并非占据整个平面镜面,所以尽管受边缘处变形影响,平面镜整体的面形精度PV值较大,但对通光口径内的面形没有显著影响.图6可以看出通光口径内面形质量远好于整体面形,平面镜边缘的变形没有影响载荷正常成像,3种模型的通光口径内静态面形均满足标准.

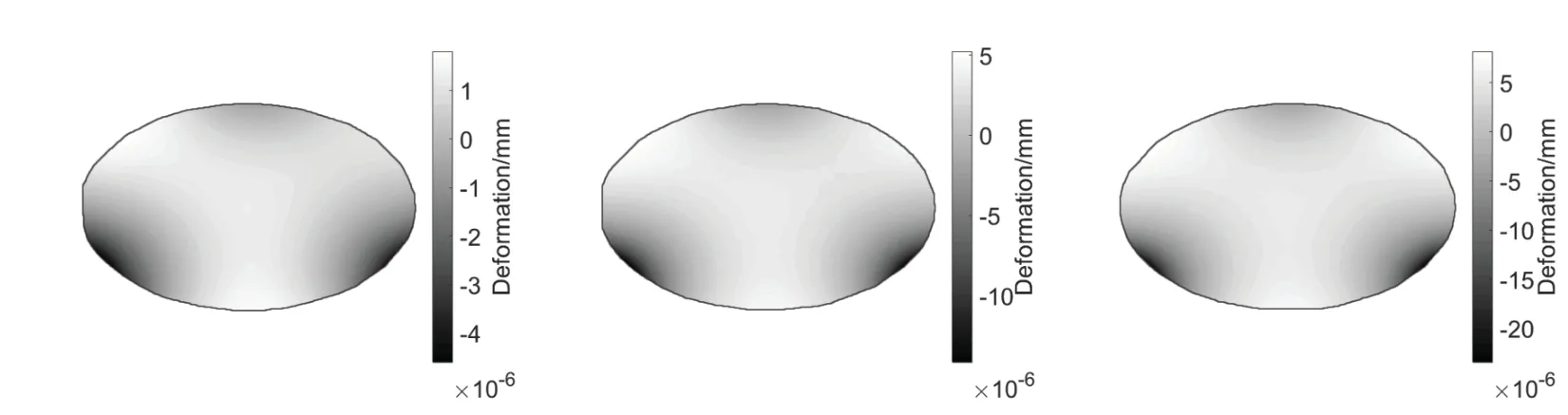
图5 模型I无重力作用通光口径内静态面形云图(左);模型II无重力作用通光口径内静态面形云图(中);模型III无重力作用通光口径内静态面形云图(右).Fig.5 The contour of Model I of static ap erture surface under zero gravity(left);the contour of Model II of static ap erture surface under zero gravity(middle);the contour of M odel III of static ap erture surface under zero gravity(right).

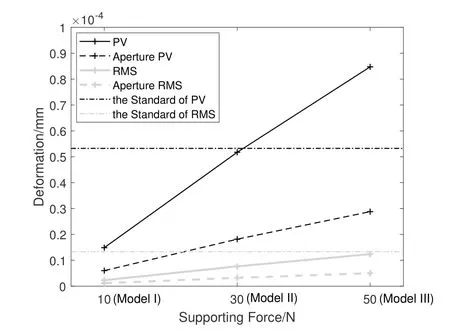
图6 整体及通光口径部分静态面形PV、RMS曲线Fig.6 PV and RMS curves of the whole and the aperture static surfaces

4.3 动力学仿真

根据设计的摆镜对日观测摆动行程及工作频率,摆动激励为ϕ=0.0001sin(2π×100×t)rad,t为时间(Time),对摆镜施加2个周期的激励,激励曲线及响应曲线如图7所示.

因为结构原因,摆镜绕Z轴水平摆动和绕Y轴竖直摆动需各自分析,对在轨无重力环境进行瞬态动力学仿真,选取关键时间节点数据[11],得到动态面形精度.摆镜绕Z轴水平摆动面形精度如表4.

篇幅关系,仅展示3种模型典型的绕Z轴水平摆动动态面形,如图8所示.

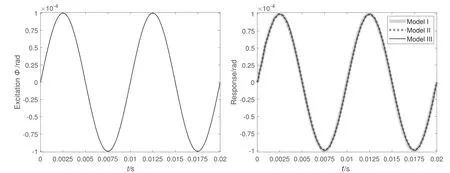
图7 激励曲线(左);模型绕Z轴摆动响应曲线(右).Fig.7 Curve of excitation(left);curve of model of Z axis swing resp onse(right).

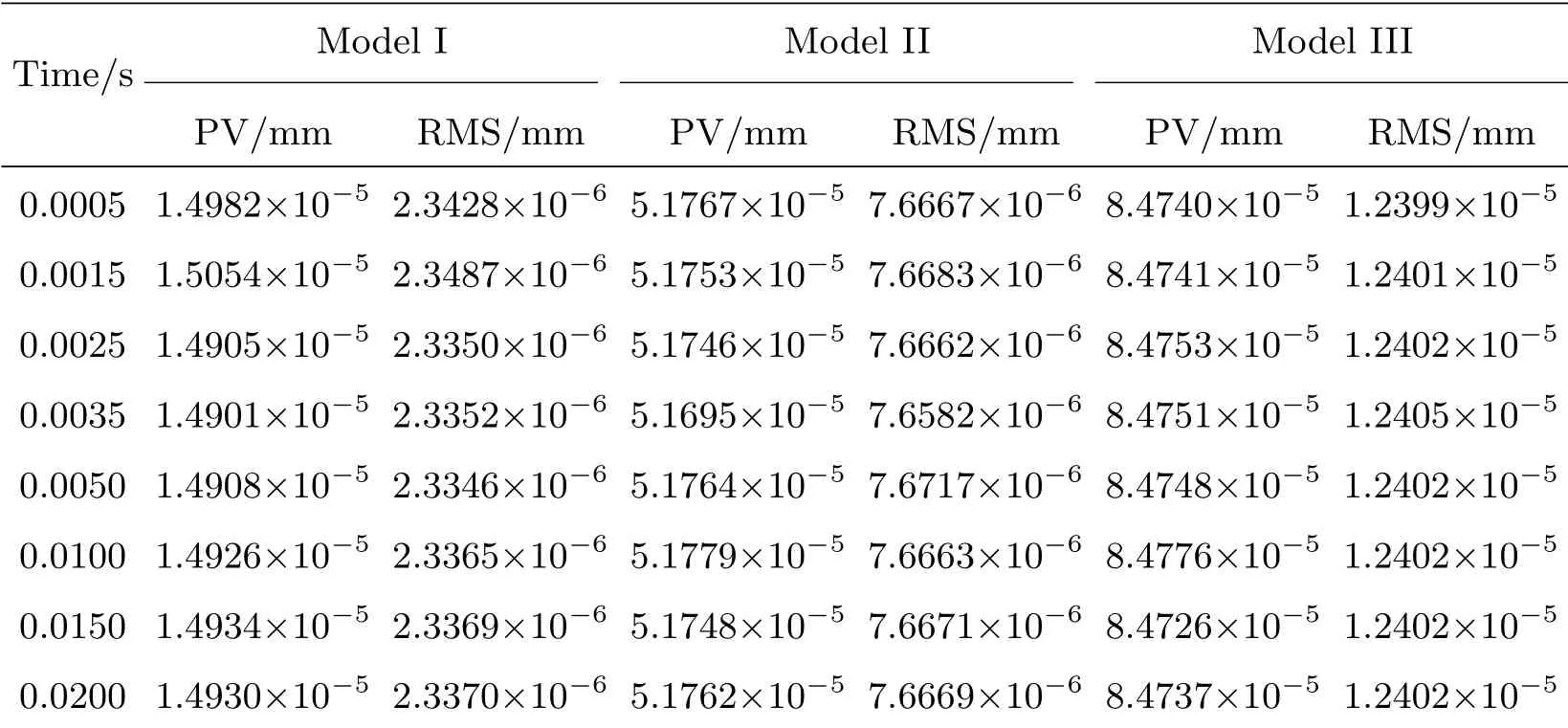
表4 在无重力作用下绕Z轴摆动的动态面形PV、RMS值Table 4 PV and RM S of d ynam ic surface und er zero grav ity at the Z ax is sw ing

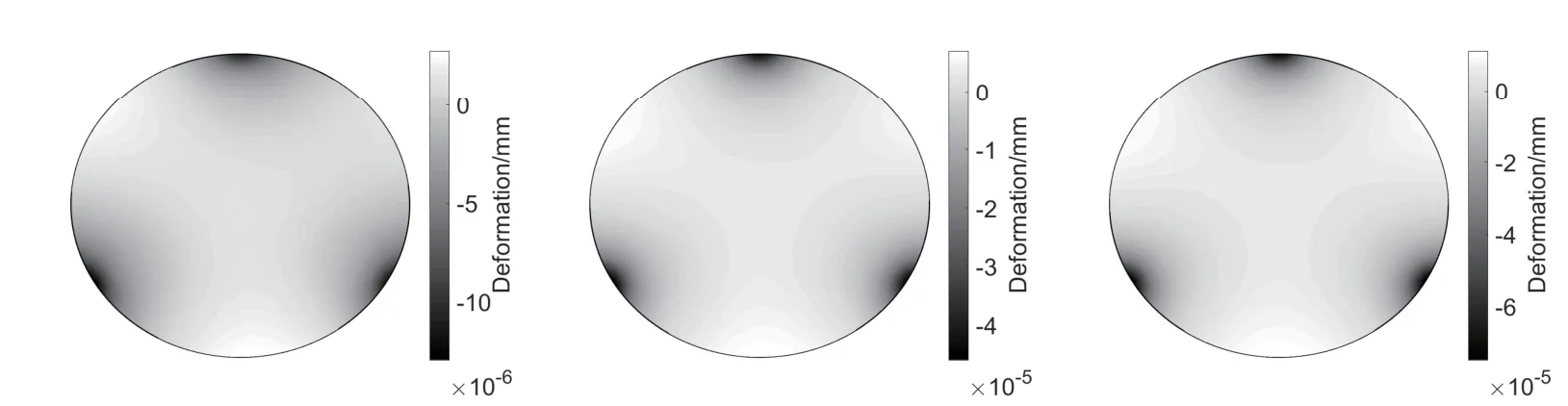
图8 模型I在无重力作用下绕Z轴摆动0.0015 s的动态面形云图(左);模型II在无重力作用下绕Z轴摆动0.0100 s的动态面形云图(中);模型III在无重力作用下绕Z轴摆动0.0100 s的动态面形云图(右).Fig.8 The contour of Model I of dynamic surface under zero gravity at the 0.0015 s Z axis swing(left);the contour of Model II of dynamic surface under zero gravity at the 0.0100 s Z axis swing(middle);the contour of Model III of dynamic surface under zero gravity at the 0.0100 s Z axis swing(right).

摆镜绕Y轴竖直摆动面形精度如表5.篇幅关系,仅展示3种模型典型的绕Y轴竖直摆动动态面形,如图9所示.

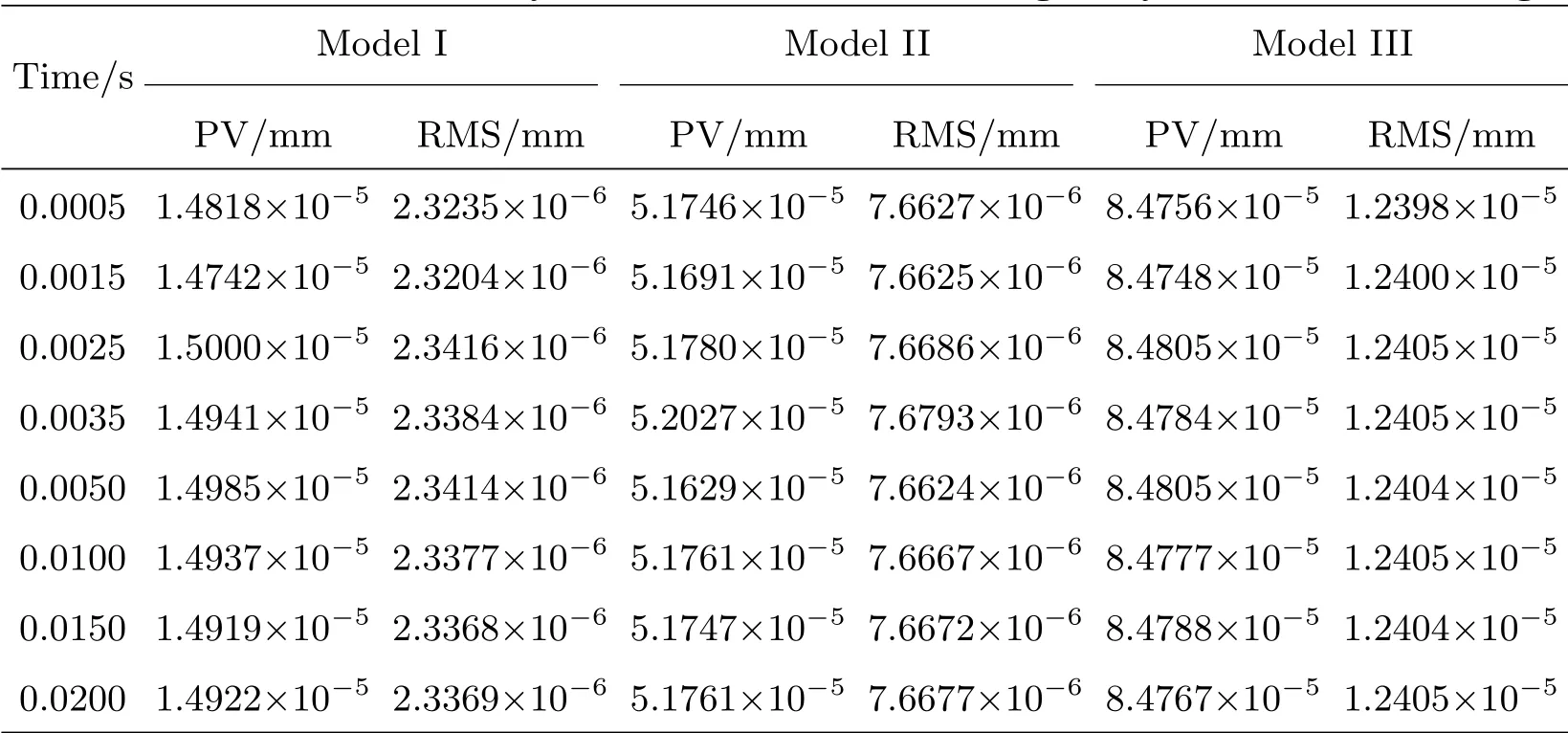
表5 在无重力作用下绕Y轴摆动的动态面形PV、RMS值Table 5 PV and RM S of d ynamic surface und er zero gravity at the Y axis swing

图9 模型I在无重力作用下绕Y轴摆动0.0025 s的动态面形云图(左);模型II在无重力作用下绕Y轴摆动0.0035 s的动态面形云图(中);模型III在无重力作用下绕Y轴摆动0.0025 s的动态面形云图(右).Fig.9 The contour of Model I of dynamic surface under zero gravity at the 0.0025 s Y axis swing(left);the contour of Model II of dynamic surface under zero gravity at the 0.0035 s Y axis swing(middle);the contour of Model III of dynamic surface under zero gravity at the 0.0025 s Y axis swing(right).

分析仿真结果,动态面形精度与压片支持力有关,受力越小,平面镜动态面形越好.根据柔性支撑的特性,柔性过大时系统刚度可能得不到保证,造成摆镜摆动时的滞后效应,且摆动幅度过大时可能会造成动态面形的急剧恶化,仿真时重点关注了此问题.

由图7可以看出,3种模型的摆镜摆动跟踪情况均较好,响应曲线与激励曲线近乎一致,未出现明显的滞后效应.

由表4–5可以看出,在外界摆动激励的作用下相同模型的面形精度在不同时刻没有显著变化,没有出现动态面形急剧恶化的现象.同时,对比不同摆动方向的动态面形精度数据,摆镜的结构对不同摆动方向的面形结果没有显著影响.由图8–9可以看出,动态面形的变形依然集中在摆镜支点嵌入平面镜的边缘处,因此变形对通光口径内面形没有显著影响.3种模型的通光口径内动态面形均满足标准.

综上,摆镜垫片厚度与压片支持力有关,较薄的垫片厚度虽然有利于改善平面镜面形,但同时垫片较薄可能会影响其在摆镜摆动过程所起的缓冲作用,造成平面镜局部应力过大甚至破损失效,因此需要对摆镜摆动过程的平面镜背部应力情况进行动力学分析.对摆镜绕Y轴竖直摆动的情形进行仿真,3种模型的平面镜背部最大应力曲线如图10(左)所示,平面镜背部应力最大处均为垫片接触部位,典型的平面镜背部应力图如图10(右)所示.

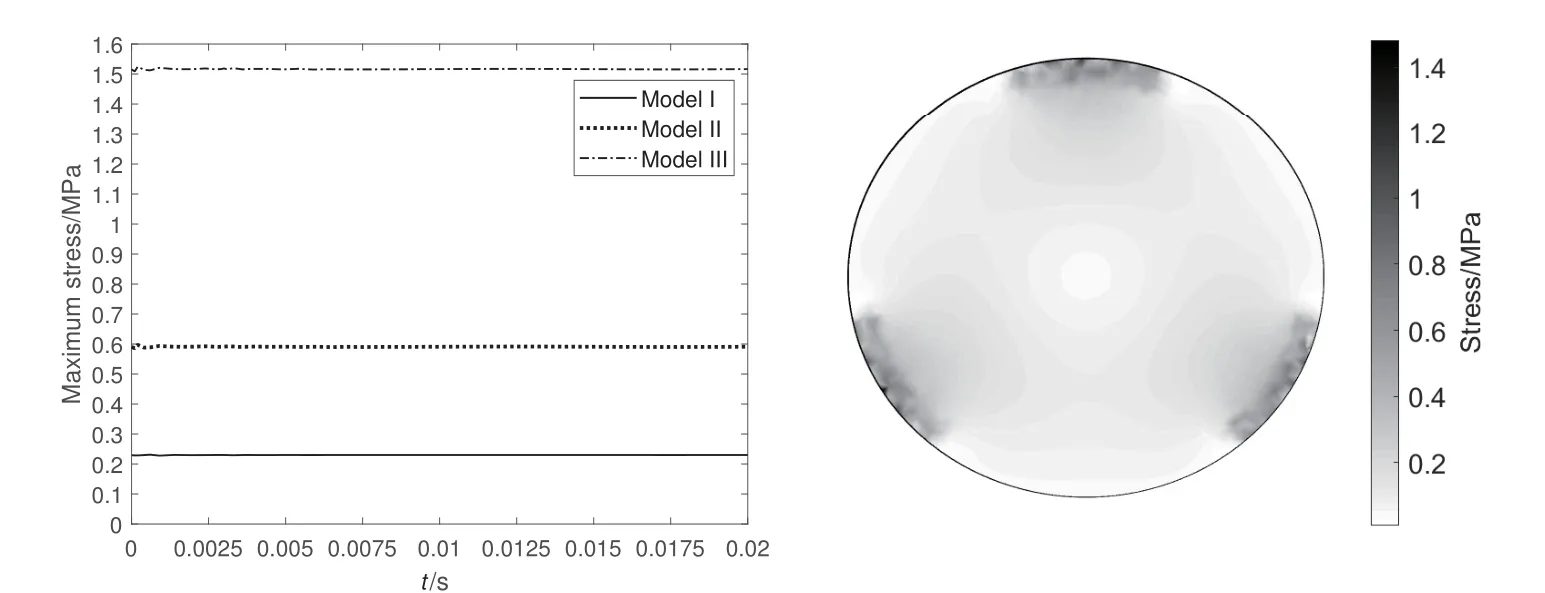
图10 平面镜背部最大应力曲线(左);模型III在无重力作用下绕Y轴摆动0.0025 s的平面镜背部应力云图(右).Fig.10 Maximum stress curves of the plane mirror back(left);the contour of Model III of plane mirror back stress under zero gravity at the 0.0025 s Y axis swing(right).

由图10可以看出,3种模型的平面镜背部最大应力差异较大,同种模型的最大应力在摆动过程中有一定波动但波动较小,3种模型随垫片厚度增加,压片支持力增大,平面镜背部最大应力也随之增大.

这说明最大应力与摆镜垫片所起的缓冲作用关系较小,与弹性压片提供的支持力关系较大,结合表2可以看出,调整压片支持力时摆镜垫片厚度仅需微调,不同模型的摆镜垫片厚度相差较小,所以可以认为3种模型垫片厚度的变化对缓冲作用的影响有限,垫片厚度减小不会导致局部应力增大.3种模型的平面镜背部最大应力均在合理范围内.

4.4 重力环境的进一步分析

结合上述分析,对仿真面形较差的模型III在地面有重力环境的面形精度作进一步分析,观察其有重力环境下面形是否进一步恶化甚至不符合光学性能要求.

将有无重力条件的模型III动态面形精度进行对比,得到的面形精度曲线如图11所示.图中Orbit指在轨无重力环境,Ground指地面有重力环境.

由图11可以看出,有无重力约束对面形没有产生显著影响,地面有重力环境下动态面形精度曲线与在轨无重力环境下曲线基本重合,通光口径内面形满足要求,认为根据模型III参数加工的摆镜机构可以正常在轨、在地面工作运行.

5 仿真结论与实验验证

综合上述仿真与分析,本文所述不同参数的3种模型均符合光学系统要求.这种利用弹性压片3点侧面柔性支撑的摆镜机构方案,可以有效改善现有采用机械连接或胶接的传统摆镜机构的缺点,且模型中的支持力只与摆镜垫片和弹性压片有关,这种与螺栓预紧力无关的特性可以减小摆镜机构装配过程的工艺难度.

为了对仿真结果加以验证,按照模型III的参数对摆镜机构进行加工,并对加工装配后的摆镜机构进行面形测试.测得的2点面形波峰波谷差(2-Point.Peak-Valley,2Pt.PV)结果为85.4280 nm,RMS值结果为12.0232 nm,最大变形位于摆镜边缘有摆镜支点嵌入处,基本与仿真结果一致,可以认为仿真数据有效.

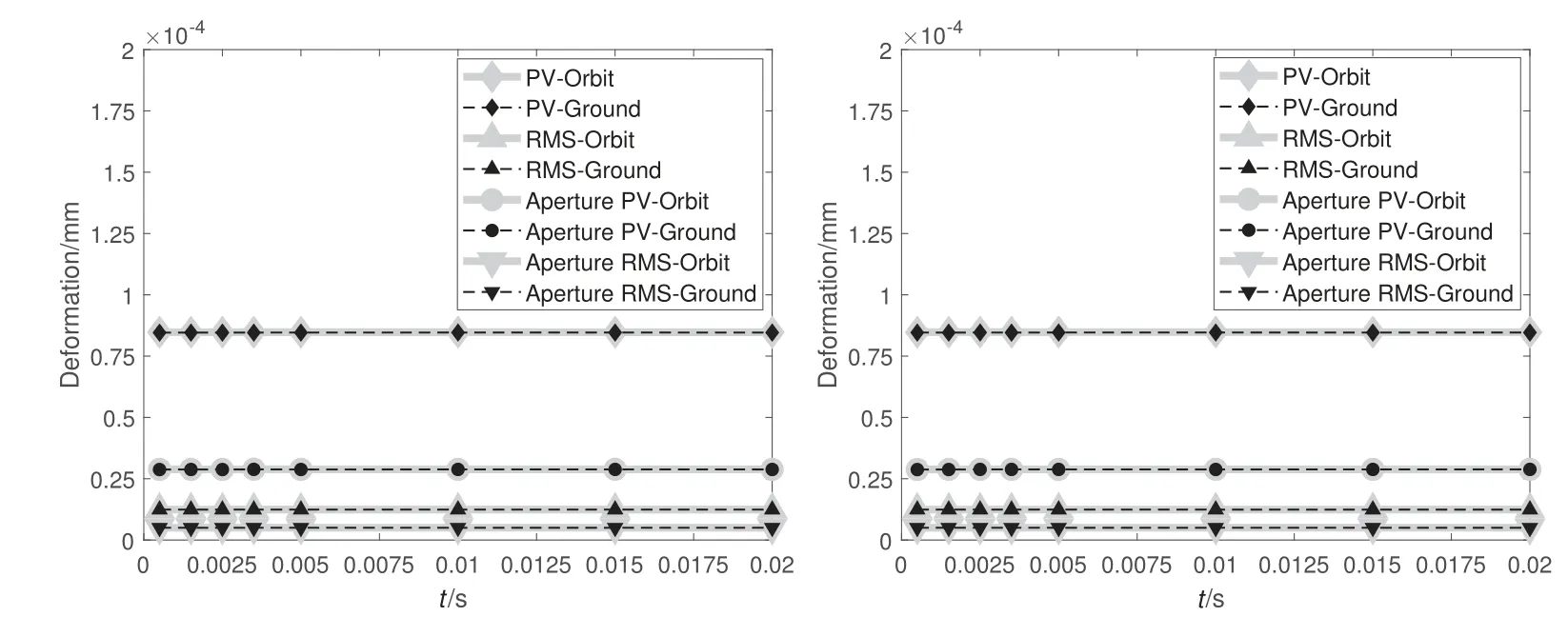
图11 模型III绕Z轴摆动的动态面形PV、RMS曲线(左);模型III绕Y轴摆动的动态面形PV、RMS曲线(右).Fig.11 PV and RMS curves of Model III of dynamic surface at the Z axis swing(left);PV and RMS curves of M odel III of dynamic surface at the Y axis swing(right).

6 结论

本文对ASO-S/FMG稳像系统的摆镜设计要求进行了分析,并据此完成利用弹性压片3点侧面柔性支撑的摆镜机构方案.通过对不同参数的结构模型进行静力学和动力学仿真,得到了摆镜在外部载荷作用下的静动态面形,并对重力作用的影响做进一步分析,仿真结果表明所设计的摆镜机构能够满足光学系统要求.在此基础上加工装配实物进一步测试,测试结果证明仿真数据有效.作为空间载荷,摆镜机构除了需要在静动力学下满足光学系统的性能要求,还需要考虑火箭发射飞行阶段的振动要求,这将在以后的工作中进一步完善.