海洋环境下湿态混凝土力学性能时变规律研究

韩 阳，刘红彪，刘现鹏

(交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室 水工构造物检测、诊断与加固技术交通行业重点实验室，天津 300456)

在交通工程建设中，混凝土结构起到了重要作用。港珠澳大桥、洋山港等超级工程的建成标志着我国交通工程已处于世界领先的地位。但混凝土结构在海洋环境下仍面临各种设计、施工和检测难题。尤其针对水下区和水位变动区不同饱和状态的湿态混凝土耐久性损伤检测和修复更为复杂。因此，准确了解海洋环境下的湿态混凝土力学性能参数随饱和度的时变规律对港口工程混凝土设计和维护具有重要意义。

目前，饱和混凝土的力学性能研究已取得较多成果，其宏观力学特性和损伤也取得了许多研究成果。陈谦[1]对饱和水工混凝土损伤及破坏进行了多项实验研究，结果表明饱和混凝土试件的抗压强度随着浸泡时间的延长而逐渐降低。徐童淋[2]等对柱体饱和混凝土试件在不同机械荷载循环作用后进行了动静态单轴压缩试验，对饱和混凝土的峰值应力和弹性模量变化趋势进行了总结。张永亮[3]等通过分离式霍普金森压杆试验和准静态试验，研究了不同饱和度混凝土强度与应变率的关系。梁辉[4]等通过饱和混凝土劈拉试验对其劈拉强度变化规律进行了研究。

非饱和的混凝土力学行为研究在近些年发展较快。Bourgeois[5]等研究了不同含水率对混凝土力学性能的影响并提出了混凝土有效力学性能的弹塑性模型； Chatterji[6]从理论角度对混凝土在水中的饱和状态进行了深入研究。Wang[7]等基于水的黏性对非饱和混凝土的有效弹性模量和泊松比进行了预测。魏新江[8]等研究了非饱和开裂混凝土中水分运移，得到了混凝土初始饱和度、裂缝宽度与渗水深度的关系。刘红彪[9]总结了非饱和混凝土宏观力学特性在力理论分析及数值计算方面存在的问题及未来的发展趋势。处于非饱和状态的湿态混凝土的宏观力学特性及其在混凝土饱和过程中的时变规律研究成果有限，因此本研究开展了对非饱和状态的湿态混凝土的轴心抗压强度、弹性模量和泊松比在不同浸泡时间下的时变规律开展试验研究，研究成果为水运工程混凝土设计和耐久性维护提供科学参考。

1 试验设计与实施

海洋环境下的混凝土构件饱和状态随时间变化而变化。初期为非饱和状态，其力学性能受周围环境影响较大。海洋环境下的混凝土设计对其饱和度分布也有较多影响。因此，结合实际工况，本文采用强度等级为C30、C40、C50和C60的混凝土立方体试块，在初始状态(未浸泡)、7 d、14 d、21 d和28 d浸泡后，开展混凝土力学性能试验。通过分析试验结果，研究湿态混凝土的轴心抗压强度、弹性模量和泊松比在不同浸泡时间下的变化规律，为水运工程混凝土设计提供科学依据与参考。

1.1 试验设计

本研究选用港工结构中常用的C30、C40、C50、C60四个强度等级的混凝土作为研究对象，其配合比见表1，试块尺寸设计见表2。为了更好的模拟海洋环境下的湿态混凝土，本研究将设计好的混凝土试块放入充满海水的浸泡池。将每种强度的混凝土试块分别浸泡7 d、14 d、21 d和28 d后开展力学性能试验。将试验数据与干燥混凝土(未浸泡)的力学性能进行对比，分析湿态混凝土在不同浸泡时间下力学性能参数的时变规律。

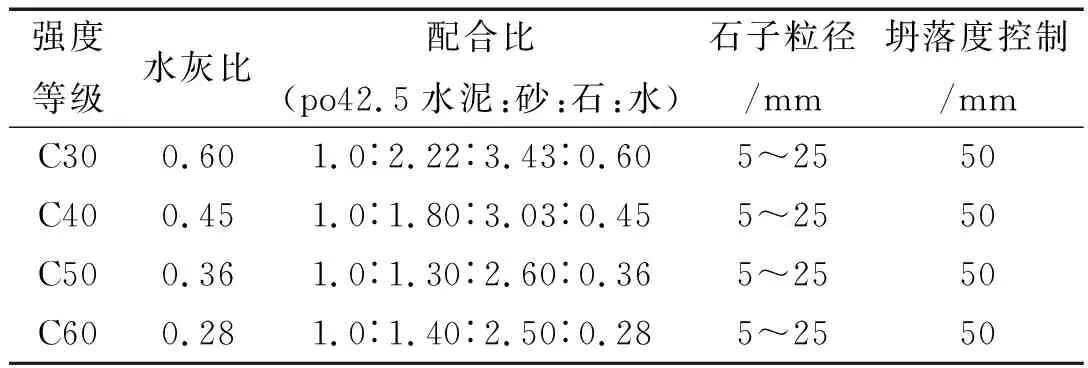
表1 混凝土配合比设计(质量比)Tab.1 Mix proportion design of the concrete (mass ratio)

表2 混凝土试块尺寸设计Tab.2 Design size of the concrete test block

1.2 试验方法

轴心抗压强度试验加载时采用0.5 MPa/s的加载速度进行试验。混凝土的弹性模量多通过试块轴心抗压试验的应力-应变曲线，采用其极限抗压强度0.4倍处的割线模量作为材料的弹性模量。而《普通混凝土力学性能试验方法标准》(GB/T50081-2002)中提供了相应试验方法，且在实际工程中应用较多。但此试验方法的试验耗时较长，对相应位移传感器的安装方法要求较高，且难以测试混凝土的泊松比。由此，采用两种试验方法，对相应混凝土试块进行了弹性模量测试，通过对比检验两种方法的差别，由此给出相关结论。

首先，选取C30、C40两种强度等级的混凝土试块进行弹性模量及泊松比测试，测试方法采用混凝土试块表面粘贴应变片的方式获取试块的应力应变曲线，测试分别采用上述两种方法进行，两种方法的主要区别在于一种是以0.5 MPa/s的加载速度直接将试块压碎，如图1所示；另一种是0.5 MPa/s的加载速度以多次往复的方式加载，如图2所示。根据上述两种方法，分别对初始状态(未浸泡)下的C30、C40混凝土进行了弹性模量和泊松比测试试验，试验结果分别见表3 和表4。

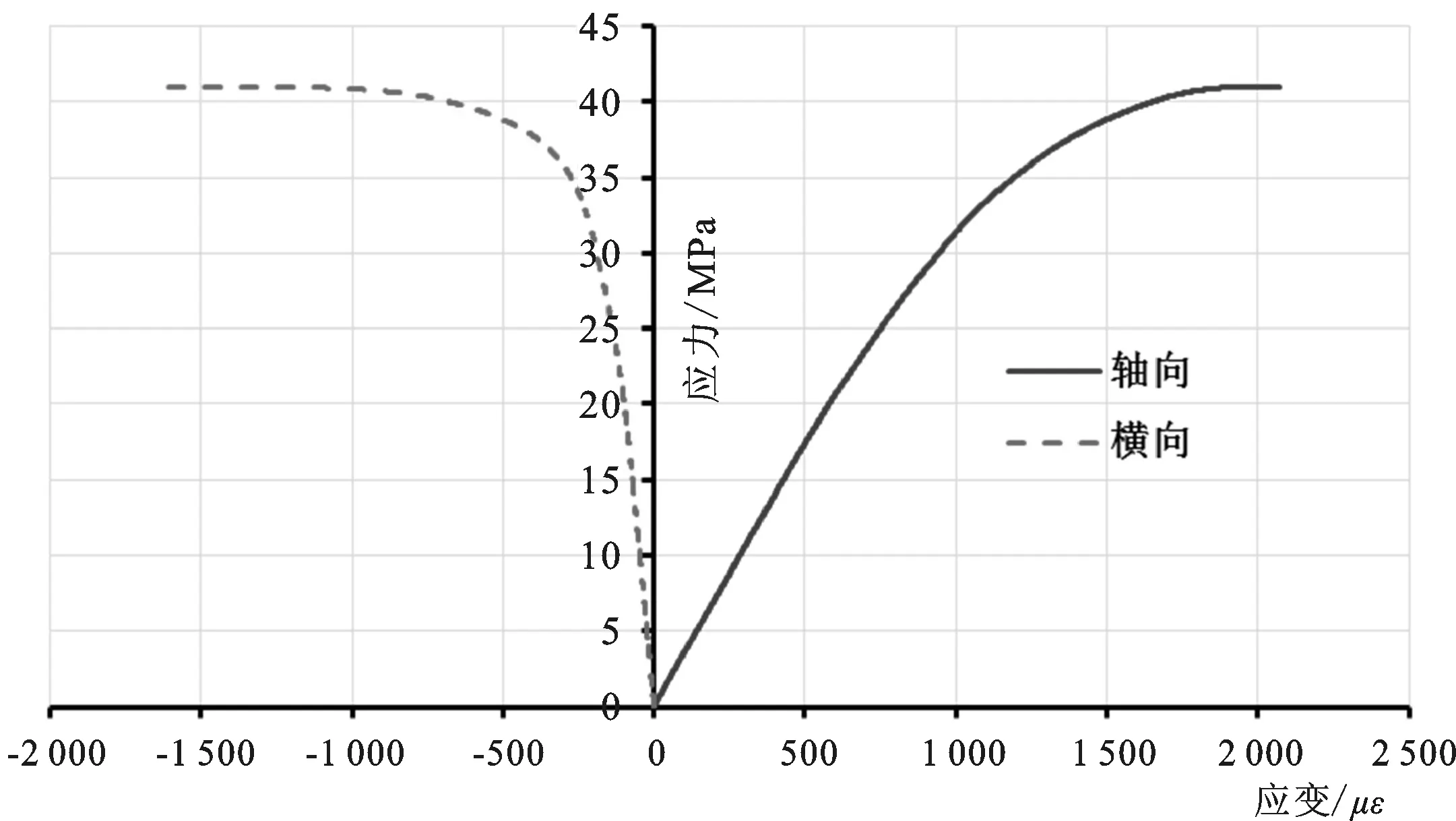
图1 C40混凝土轴心抗压强度的应力-应变曲线(一次性压坏)Fig.1 Stress-strain curve of axial compressive strength of C40 concrete(One time loading)

图2 C40混凝土轴心抗压强度的应力-应变曲线(往复加载)Fig.2 Stress-strain curve of axial compressive strength of C40 concrete(Cyclic loading)

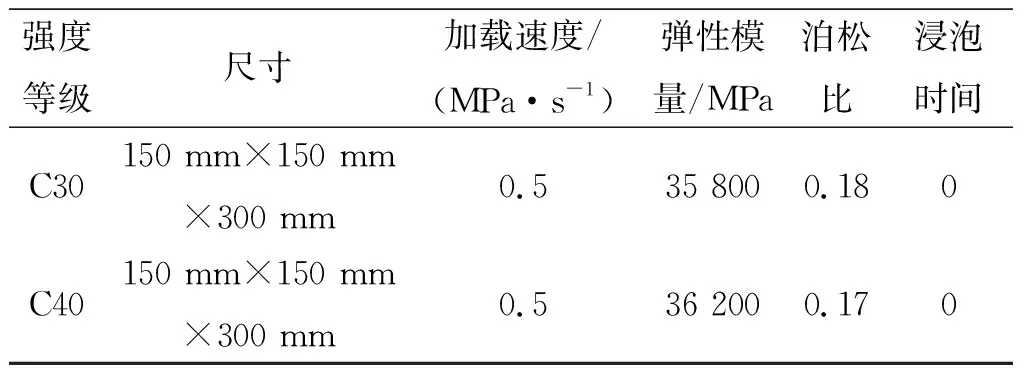
表3 C30和C40混凝土弹性模量及泊松比测试值(一次性压坏)Tab.3 Test values of elastic modulus and Poisson′s ratio of C30 and C40 concrete(One time loading)

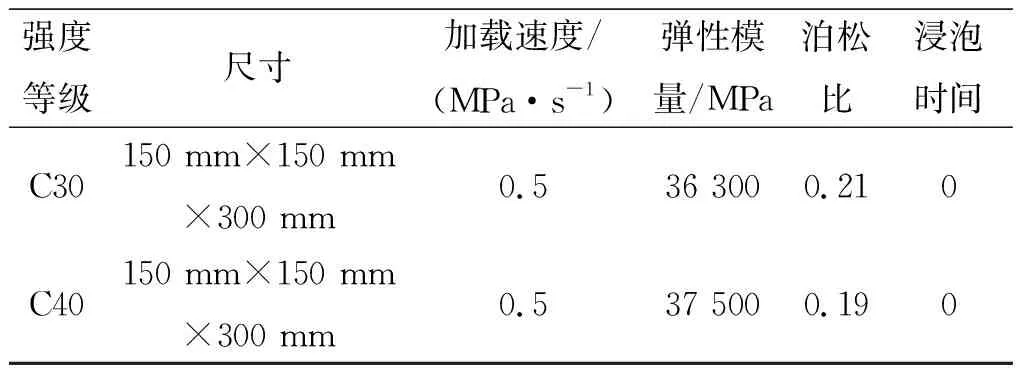
表4 C30和C40混凝土弹性模量及泊松比测试值(往复加载)Tab.4 Test values of elastic modulus and Poisson′s ratio of C30 and C40 concrete(Cyclic loading)

由上表可知，采用一次性压坏的方式进行混凝土弹性模量及泊松比的测试，测试结果与《混凝土结构设计规范》(GB50010-2010)提供的混凝土弹性模量值更接近，而采用往复加载的模式测试，弹性模量的测试结果偏大，因此，本文测试混凝土弹性模量及泊松比时，采用一次性加载破坏的方式进行，弹性模量采用极限抗压强度0.4倍处应力-应变曲线的割线模量。

2 试验数据分析

2.1 混凝土轴心抗压强度

试验结果见表5，每种混凝土强度的时变规律曲线见图3。由图3可知：C30混凝土在经21 d海水浸泡后，强度降到最低，28 d浸泡后强度又有所上升，总体比未浸泡时强度降低了4.7 MPa，降低了13.7%；C40混凝土在经7 d海水浸泡后，强度下降了1 MPa，到达14 d后强度又上升了0.6 MPa，随后强度开始下降，最终强度降低了3.6 MPa，降低了9.8%；C50混凝土在14 d海水浸泡内，强度呈下降趋势，到达21 d又有所上升，随后强度又呈下降趋势，28 d后强度降低了2.8 MPa，降低了7.2%；C60混凝土在14 d海水浸泡内强度呈下降趋势，随后强度又有所提高，28 d后强度比初始状态(未浸泡)降低了3.3 MPa，降低了8.2%。

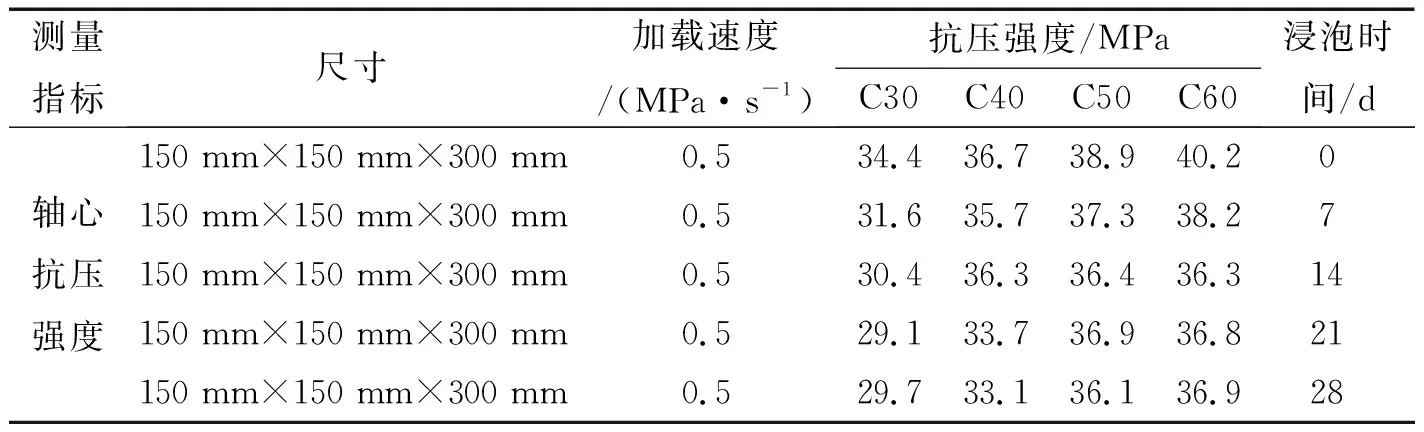
表5 不同浸泡时间下的混凝土轴心抗压强度的时变规律Tab.5 Change rule of the axial compressive strength under different soaking time

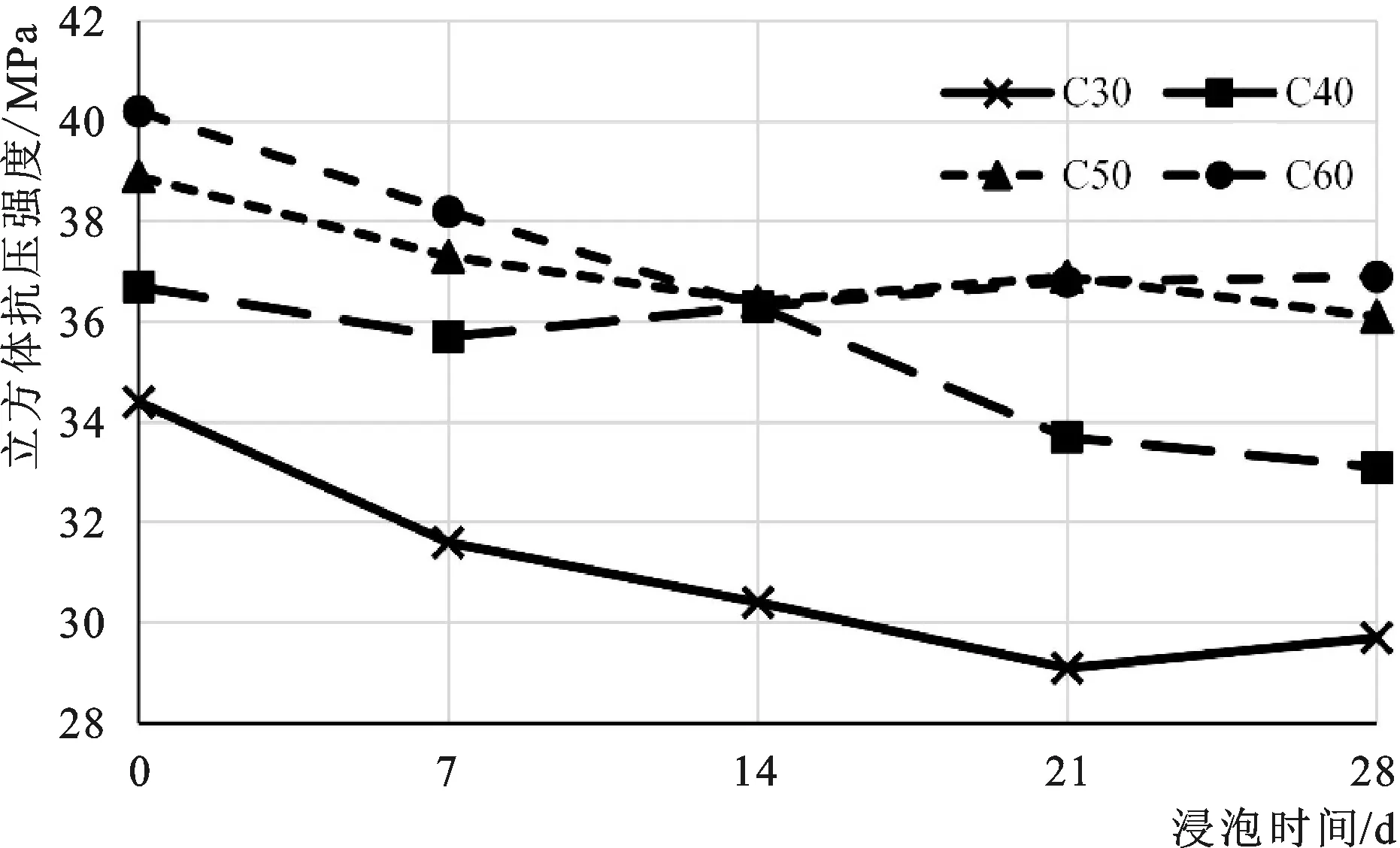
图3 不同等级混凝土轴心抗压强度的时变曲线Fig.3 Curve over time of axial compressive strength of concrete by different grades

综上所述，4种强度的混凝土单轴轴心抗压强度在浸泡28 d内变化趋势较多，到达28 d时强度较初始状态(未浸泡)均下降，下降比例在7%～14%之间。

为了验证本文研究成果，选取参考文献[1]中三组C30混凝土试件在浸泡7 d、15 d和30 d三个阶段后的抗压强度与本文进行对比(见表6和图4)。通过对比分析可知，浸泡阶段2的强度均呈下降趋势。其中试件三下降比例最大为10.41%。浸泡阶段2到浸泡阶段3，本文和试件一均呈下降趋势，而试件二和试件三呈上升趋势。对比饱和状态后的强度，试件二强度几乎未发生变化；其他试件强度下降比例为4.11%、5.11%和6.01%，说明本文针对抗压强度的试验结果准确。

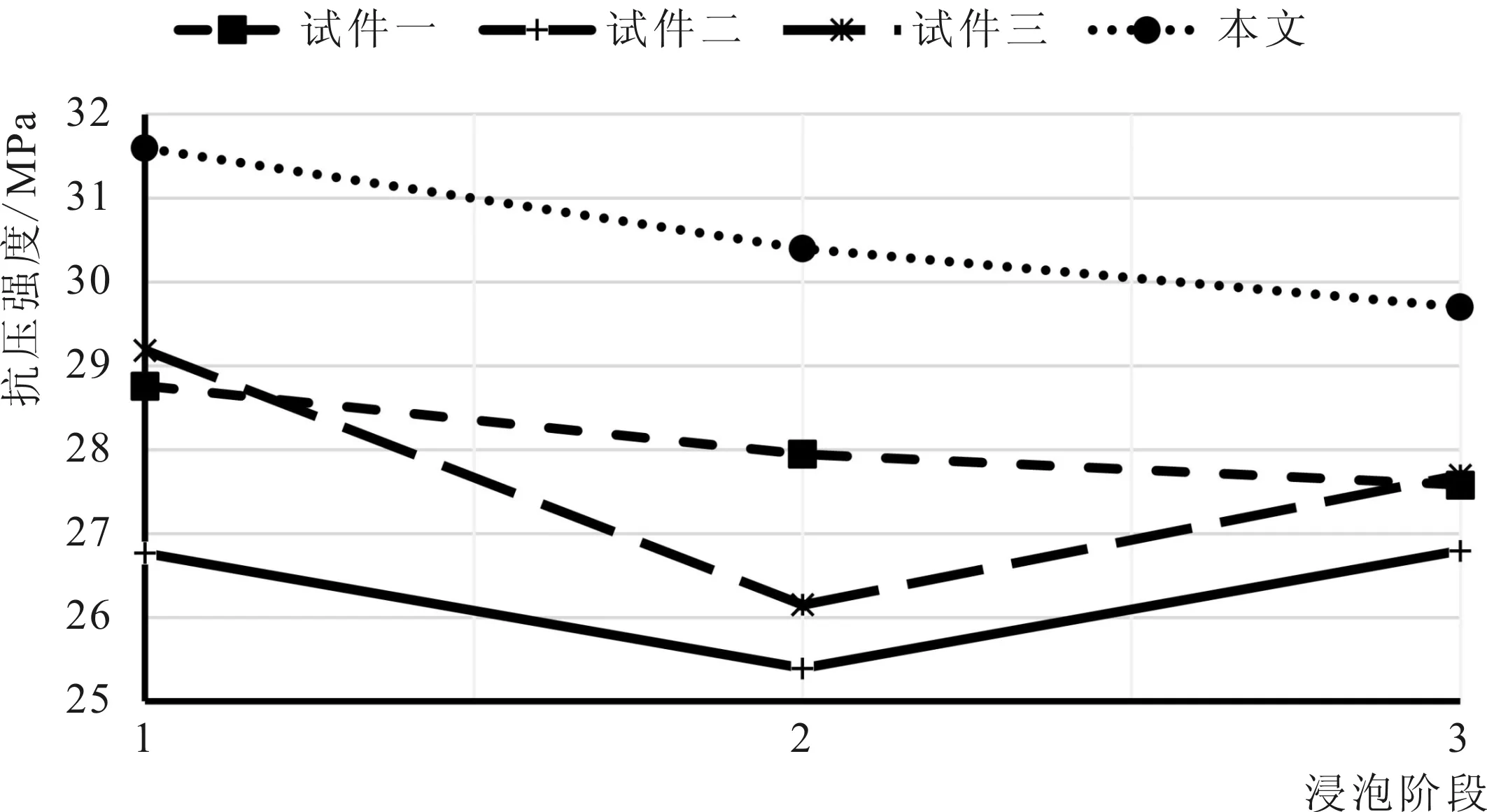
图4 文献1 C30混凝土轴心抗压强度的时变曲线Fig.4 Curve over time of axial compressive strength of concrete by C30 in Ref.1

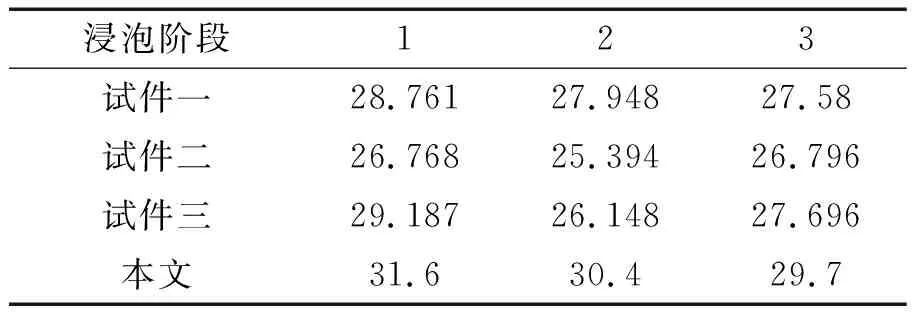
表6 参考文献[1]不同浸泡时间下的C30混凝土轴心抗压强度的时变规律Tab.6 Change rule of the axial compressive strength of C30 concrete under different soaking time in Ref.1

2.2 混凝土弹性模量与泊松比

为了分析不同强度等级的混凝土在不同浸泡时间内的强度时变规律，将C30、C40、C50、C60四个强度等级的混凝土在浸泡时间分别为初始状态(未浸泡)、7 d、14 d、21 d、28 d的弹性模量及泊松比测试值进行曲线绘制，每种混凝土的弹性模量及泊松比试验数据见表7，时变规律曲线见图5和图6。

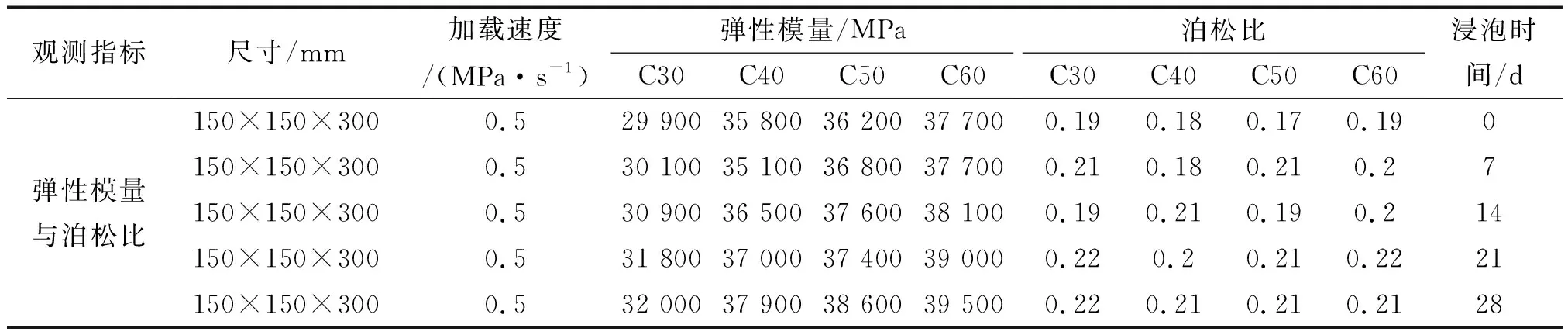
表7 不同浸泡时间下的混凝土弹性模量及泊松比测试值Tab.7 Change rule of elastic modulus and Poisson′s ratio under different soaking time

(1)弹性模量。

C30混凝土弹性模量在28 d的海水浸泡时间内一直呈上升趋势，28 d弹性模量强度升高了2 100 MPa，升高比例为7.0%；C40混凝土弹性模量在7 d内呈下降趋势，随后弹性模量升高，最终在28 d时较初始状态(未浸泡)升高了2 100 MPa，升高比例为7.0%；C50混凝土弹性模量在14 d内呈上升趋势，到达21 d又有所下降，随后又开始升高，到达28 d时较初始状态(未浸泡)升高了2 400 MPa，升高比例为6.6%；C60混凝土弹性模量到达7 d时未发生变化，随后一直呈上升趋势，到达28 d时较初始状态(未浸泡)弹性模量升高了1 800 MPa，上升比例为4.8%。

(2)泊松比。

C30混凝土泊松比在7 d内呈上升趋势，7～14 d又转为下降趋势，14～21 d呈上升趋势，21～28 d进入平稳状态。最终泊松比较初始状态(未浸泡)时升高了0.03，升高比例为15.8%；C40混凝土泊松比在7 d内未发生变化，7～14 d呈上升趋势，14～21 d又有所下降，21～28 d又呈上升趋势，最终泊松比较初始状态(未浸泡)时升高了0.03，提升比例为16.7%；C50混凝土泊松比变化趋势与C30基本一致，均为先上升，又下降，随后又上升，不同的是在到达21 d后，其泊松比未发生变化，最终泊松比较初始状态(未浸泡)时升高了0.04，提升比例为23.5%；C50混凝土泊松比在21 d内基本保持上升趋势，21～28 d呈下降趋势，最终泊松比较初始状态(未浸泡)时升高了0.02，提升比例为10.5%。

综上所述，通过对C30、C40、C50、C60混凝土的海水浸泡试验可知，随着浸泡时间的增长，混凝土的弹性模量和泊松比逐渐升高；根据浸泡28 d后的试验可知，混凝土单轴弹性模量升高比例均在5%～7%之间，泊松比升高比例在10.5%～23.5%。

3 结论

本研究通过对不同浸泡时间下C30、C40、C50、C60四种等级混凝土开展力学性能试验，得到了其轴心抗压强度、弹性模量和泊松比随饱和状态的时变规律。4种强度的混凝土单轴轴心抗压强度在浸泡28 d内变化趋势较多，到达28 d时强度较初始状态(未浸泡)降低比例在7%～14%。根据现行《港口水工建筑物修补加固技术规范》(JTS311-2011)规定，对修补用的混凝土要采用相对原构件混凝土强度提高一级的材料，那么对于水下区或水位变动区的混凝土则需要考虑饱和状态下混凝土强度降低因素，防止修复加固失效或性能不足。4种强度混凝土的弹性模量和泊松比浸泡28 d内变化趋势较多，到达28 d时强度较初始状态(未浸泡)均上升；4种强度混凝土单轴弹性模量升高比例在5%～7%，泊松比升高比例在10.5%～23.5%。同时，根据试验可知，采用往复加载方式测试得到的混凝土弹性模量较一次性压坏的加载方式获取的偏大，且采用一次性压坏的方式进行混凝土弹性模量及泊松比的测试，测试结果与规范提供的混凝土弹性模量值更接近，因此，本文建议测试混凝土弹性模量及泊松比时，采用一次性加载破坏的方式进行，弹性模量采用极限抗压强度0.4倍处应力-应变曲线的割线模量。总之，饱和状态下混凝土的力学性能时变规律研究成果对于水运工程的混凝土设计和加固维护等都具有重要意义。