基于δ-SPH方法的多孔潜堤共振反射数值模拟研究

史宝凯，陈永焜，刘 勇，DOMENICO D. MERINGOLO

(中国海洋大学 山东省海洋工程重点实验室，青岛 266100)

堆石防波堤是一种常见的海岸工程结构，由于孔隙的存在，该结构不仅能衰减波浪，也使水体交换成为可能。在理论和数值分析中，由于块石形状及分布等较为复杂，通常将其简化为具有各向同性的可渗多孔介质[1]。为了在防御波浪侵袭、保护岸线的同时不影响近岸景观和水质交换，可以采用潜堤代替出水堤[2]。但是单个多孔潜堤有可能无法满足防护需求，可布置多排潜堤，利用多排潜堤的Bragg共振反射效应提高掩护效果。从19世纪70年代开始，部分学者发现天然海滩上平行于海岸的系列沙波由于Bragg共振反射作用，具有良好的掩护效果。Kirby[3]使用拓展的缓坡方程，研究了波浪在单、双周期正弦沙波上传播的共振反射，模拟结果与试验结果符合较好。Dalrymple和Kirby[4]考虑波浪入射方向，使用边界积分法研究了斜向入射波在单周期正弦沙波上传播的共振反射，结果表明该方法能准确模拟较大扰动的沙波地形。Cho等[5]和Jeon等[6]分别通过物理模型试验和VOF方法探究了多排平行潜堤的反射系数与入射波长的关系，结果表明可渗透潜堤反射系数略小于不可渗透潜堤反射系数，共振反射效应能有效提升潜堤掩护效果，并推荐使用梯形潜堤。魏欣[7]基于物理模型试验和Boussinesq方程数值模型，研究了双排梯形潜堤的反射系数与水深、潜堤坡度及其间距等因素的关系。

现有数值模拟研究多基于网格方法，在处理流体大变形等情况时对网格要求很高，因此本文选择SPH(光滑粒子流体动力学)研究多孔潜堤的共振反射现象。该方法由Monaghan[8]提出，是一种无网格Lagerange粒子法。目前已有很多学者利用SPH方法进行了研究，Shao等[9]通过多孔介质内外采用不同的控制方程，使用SPH模型研究了波浪与多孔介质防波堤的相互作用。Akbari等[10]通过引入表征物理量的概念，将多孔介质内外统一为一套控制方程，研究了波浪在多孔介质斜坡堤上的爬坡和越浪过程。Ren等[11]使用体平均/密度权平均Navier-Stokes方程和LES模型，模拟了波浪通过多孔潜堤和出水堤的过程。为解决WCSPH(弱可压缩SPH)模型中的压力震荡问题，Antuono等[12]在控制方程中加入扩散项，提出了δ-SPH模型。经过证明，δ-SPH模型是一种准确、稳定的数值计算方法，近年来也得到了越来越多的关注，被应用于研究自由表面流动[13]、开孔沉箱[14]、液舱晃荡[15]等问题。

考虑人工抛石潜堤和天然沙波、珊瑚礁等的渗透性都会对波浪运动产生不可忽视的影响；同时，可以利用共振反射增强潜堤的掩护效果。本文将建立多孔介质的δ-SPH数值模型，研究多孔潜堤共振反射问题，分析波高、水深、潜堤参数等对潜堤共振反射的影响，为工程设计提供参考。

1 δ-SPH数值模型

1.1 控制方程

在δ-SPH[12]数值模型中将流体假定为弱可压缩的粘性流体，满足质量守恒和动量守恒，控制方程为连续方程和Navier-Stokes方程。本文引入表征物理量概念，通过在控制方程中引入阻力项，得到方程如下

(1)

(2)

式中：ρ为水的密度，kg/m3；u为表征速度，m/s，表现为流场的真实速度与孔隙率的乘积；nw为孔隙率；P为压力，Pa；g表示重力加速度，m/s2；ϑ表示粘度耗散项；α1与α2分别为多孔介质的层流和紊流阻力系数。

压力和密度之间的关系通过以下状态方程显式求解

(3)

式中：c0表示人工声速，其取值要保证密度变化率和时间增量均控制在合理范围之内；ρ0表示流体的初始密度，取值为1 000 kg/m3。

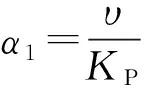
(4)

(5)

式中：d50表示多孔介质的中值粒径。

利用SPH方法对式(1)和式(2)进行离散，得到离散后的控制方程为

(6)

(7)

由于流体的弱可压缩性，在模拟冲击问题时会出现压力震荡现象。动量方程中等号右侧第三项为人工粘度项，可以使部分冲击表面上的动能转化为热能从而减少震荡。根据Monaghan等[19]建议，参数取值如下

(8)

(9)

连续性方程中等号右侧第二项为δ-SPH方法引入的扩散项，可以进一步降低传统SPH方法在模拟流体压强场时可压缩性带来的异常高频震荡，ψij为密度差值项，可简单表示为ψij=ρj-ρi。

为了兼顾准确性和效率，采用龙格库塔方法进行时间积分[20]。同时，为了进一步保证流场压力稳定，每运行30个时间步，采用下式对粒子属性进行平滑处理

(10)

式中：WjMLS是指MLS (Moving Least Square) 核函数

(11)

1.2 数值造波与消波

为得到稳定的规则波波列，避免数值水槽内发生二次反射，本文采用动量源造波方法[21]进行造波，并在水槽两端各设置一个阻尼区域用以吸收波浪，防止波浪反射[22]。对于二维数值波浪水槽，动量源造波项S=(Sx，0)表达形式为

(12)

式中：ξ=20/Wsc2，Wsc为造波区宽度，一般取为目标波波长；ω为波浪圆频率；D为源函数量，可表示为

(13)

为吸收阻尼区域内的波浪，在阻尼区域的动量方程中加入一阻尼耗散项，该项表达形式为

(14)

式中：Was为消波区的布置宽度，x0为消波区入口的横坐标。

2 数值模型验证

2.1 数值波浪水槽设置

图1给出了数值波浪水槽及潜堤的示意图。二维水槽长32 m，高0.8 m，距左壁7 m处布置一造波源，距造波源8 m处放置两排梯形多孔防波堤，堤前3.5 m外设置两浪高仪，其间距在满足利用Goda方法[23]分离入反射波计算要求的前提下，根据波况不同进行调整。水槽左右两端为人工消波区域。试验布置参考魏鑫[7]的物理模型试验并加以拓展，水深0.4～0.6 m，波高0.04～0.06 m，潜堤中心间距W为1.8 m、2.3 m和2.8 m。单个潜堤断面为如图1中所示的梯形(部分工况下退化为矩形或三角形断面)，顶宽为wt，底宽为wb，高度为wh，斜坡坡度为δk，堤顶水深ht=h-wh。组成潜堤的多孔介质孔隙率取0.42，中值粒径为1.7 cm。全部数值试验工况设计见表1。

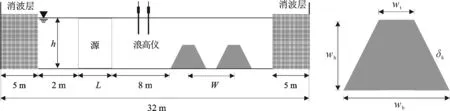
图1 数值水槽布置及潜堤几何参数Fig.1 Layout of computational domain and parameters of breakwaters

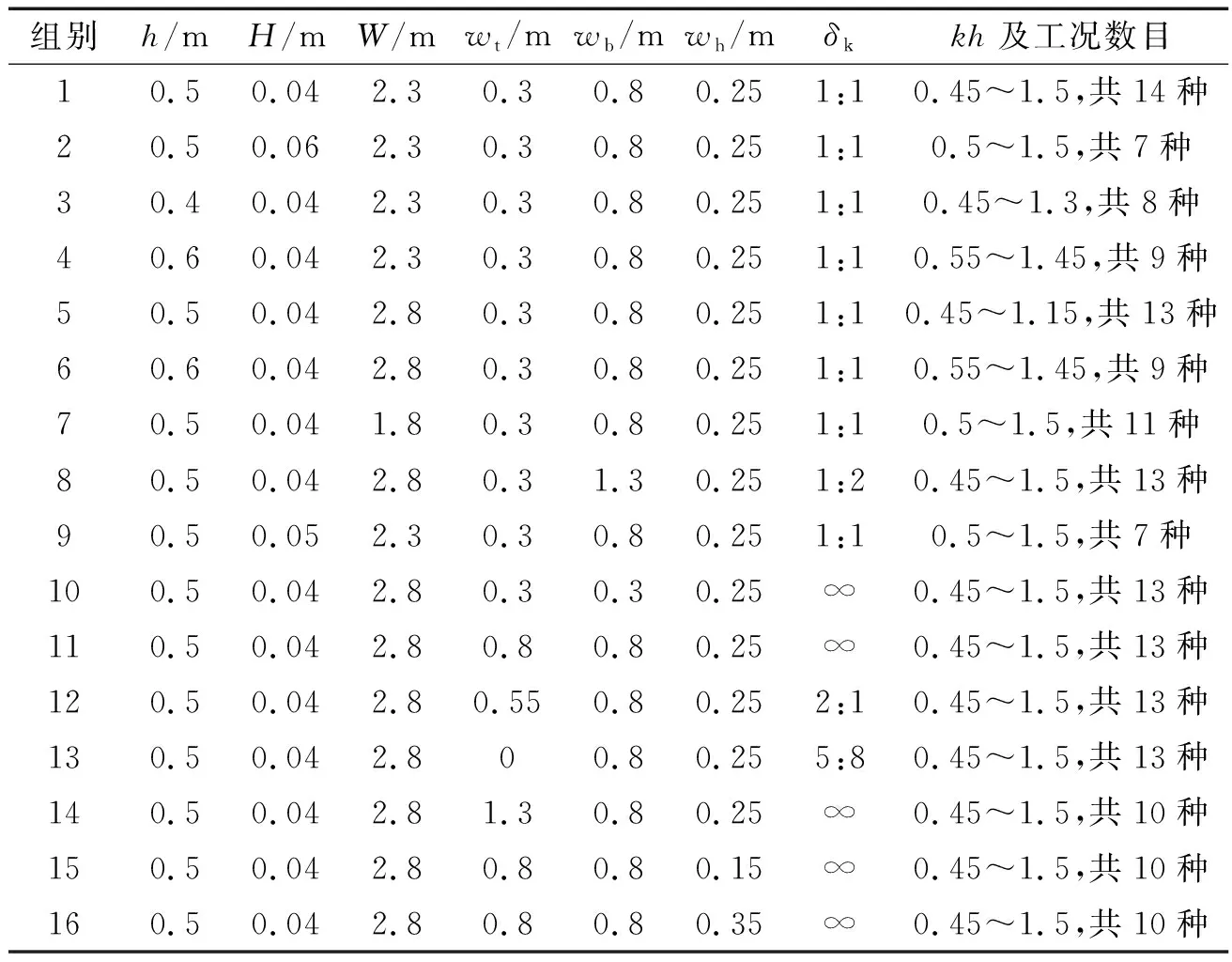
表1 试验工况设计Tab.1 Design of experimental conditions

2.2 数值结果验证

本节选取典型波浪条件(h=0.5 m，H=0.04 m)，将双排多孔潜堤反射系数的数值模拟结果与试验结果[7]进行对比，验证数值模型的合理性。潜堤反射系数利用Goda方法[23]分析得到，并且取至少10个稳定波浪作为输入数据。图2给出了四组工况下数值模拟结果与试验结果[7]的对比，图中圆点为数值模拟结果，方点为物模试验结果，可以看出二者符合良好。从图2中还可以看出，随着kh值不断增大(对应的波浪周期不断减小)，潜堤反射系数先后出现大小两个峰值，前者为主频反射，后者为次频反射。这一现象即为典型的Bragg共振反射现象，表现为当波浪在周期性连续变化的地形上传播时，二者在特定情况下会发生共振，使得波浪反射效应达到最强。

为了进一步验证数值模型的合理性，在工况W=1.8 m,δk=1∶1下主频共振时如图3所示布置浪高仪，G1～G5浪高仪与1号潜堤前趾在波浪传播方向上的距离分别为0.4 m、1.05 m、1.55 m、2.2 m和3.2 m。图4给出该工况下波面变化数值模拟结果和试验结果[7]对比。从图4中可以看出，数值模拟结果与试验结果符合良好。同时可看出波浪在经过G1和G4测点时，由于潜堤的存在使得波面出现抬升；G5测点处波形前倾，表明该处波面非线性增强，且此处波高较入射波高变小，说明发生共振反射时，双排潜堤掩护效果较好。

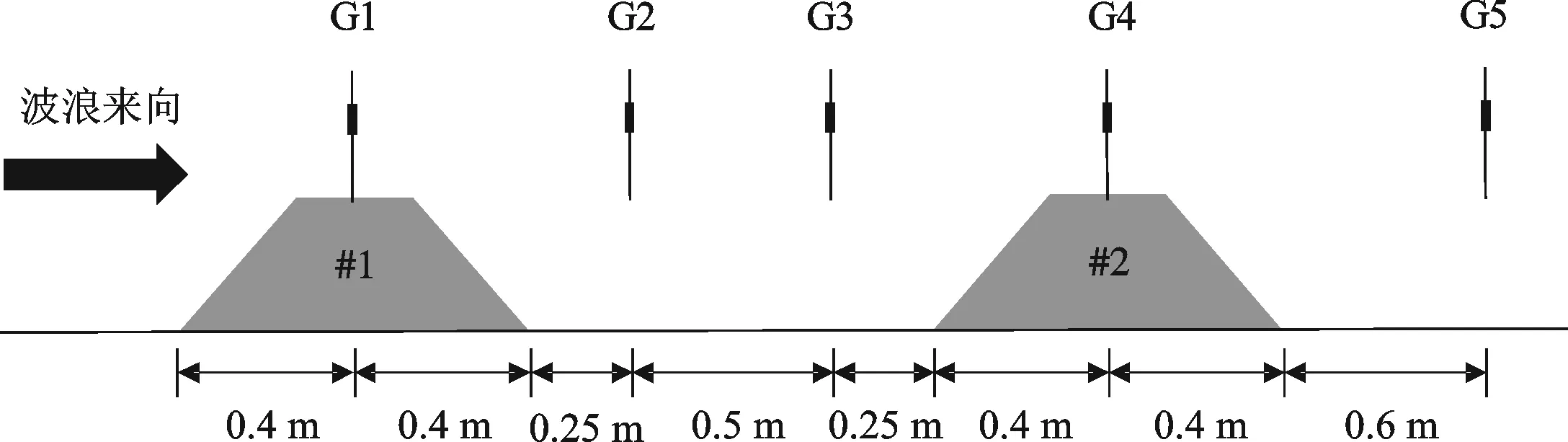
图3 浪高仪布置示意Fig.3 Arrangement of wave altimeter gages

注：h=0.5 m,H=0.04 m,W=1.8 m,wb=0.8 m,wh=0.25 m,δk=1:1,kh= 0.8图4 不同测点处波面历时曲线的数值模拟结果和试验结果[7]对比Fig.4 Comparisons of free surface elevations at different wave gauges between the numerical and experimental results[7]

3 算例分析与讨论

3.1 Bragg共振反射发生条件

表2给出了主频反射发生时，波长L与2倍潜堤中心间距W的比值关系。从表中可看出：各组L/2W的数值在1.0附近波动，即当波长约等于2倍潜堤中心间距时，双排多孔潜堤发生主频共振反射。

表2 主频共振反射条件Tab.2 Main resonance reflection conditions

3.2 入射波高对反射系数的影响

图5给出了h=0.5 m，W=2.3 m，wb=0.8 m，wh=0.25 m，δk= 1:1时，不同入射波高条件下，反射系数KR随kh值的变化曲线(分别对应1、2、9工况)。在数值试验过程中未观察到波浪破碎现象。从图5可以看出：相对波高H/h= 0.08 、0.10和0.12情况下的反射系数变化曲线基本重合，说明在波浪未破碎时，波高变化对共振反射影响较小。

3.3 堤顶水深对反射系数的影响

潜堤高度固定时，总水深h的变化会导致堤顶水深ht的变化。图6-a、6-b分别给出了H=0.04 m，wb= 0.8 m，wh= 0.25 m，δk=1∶1，W=2.3 m和2.8 m时，不同相对堤顶水深情况下反射系数KR随kh值的变化曲线(分别对应1、3、4和5、6工况)。从图6中可以看出：随着相对堤顶水深增加，反射系数整体减小，主要因为波浪的能量集中在水体表层，水深增加会降低潜堤对波浪的影响效果，降低反射系数；共振反射发生点向kh增大方向移动，这是因为潜堤包括中心间距在内的整体布置不变，主频反射时波长仍为2倍潜堤中心间距，水深的增加使得主频反射发生时的kh值同步增加。

考虑将水深固定，改变潜堤高度，图7给出了h=0.5 m，H= 0.04 m，W=2.3 m，wb= 0.8 m，δk=∞时，不同矩形潜堤高度情况下反射系数KR随kh值的变化曲线(分别对应11、15、16工况)。从图7中可以看出：潜堤高度增加导致堤顶水深减小，会引起反射系数整体增大，但并未影响发生主频反射时的波浪频率。

3.4 潜堤中心间距对反射系数的影响

图8-a、8-b分别给出了H=0.04 m，wb= 0.8 m，wh= 0.25 m，δk=1:1，h=0.5 m和0.6 m时，不同潜堤中心间距情况下反射系数KR随kh值的变化曲线(分别对应1、5、7和4、6工况)。从图8中可以看出：随着中心间距增大，主频反射和次频反射点均向kh减小方向移动，这仍然是由发生共振反射时波长与潜堤中心间距之比规律决定；主频反射附近曲线的峰值更加突出，但是有效反射频带宽度变小，说明反射效果更好但作用的波长范围减小；中心间距增加会引起主、次频反射系数峰值增大，但前者所受影响较小，后者增大现象更为明显。

3.5 潜堤宽度对反射系数的影响

为了探究潜堤宽度对共振反射的影响，本节选取矩形潜堤作为研究对象。图9给出了h=0.5 m，H=0.04 m，W=2.8 m，wh= 0.25 m，δk=∞时，不同潜堤宽度条件下反射系数KR随kh值的变化曲线(分别对应10、11、14工况)。从图9可以看出：潜堤宽度的增大使得主频反射系数增加，而相应的次频反射系数却略有减小；主频反射系数峰值点向kh减小方向移动，主频共振反射发生时波长与2倍潜堤中心间距之比变大。

3.6 潜堤坡度对反射系数的影响

潜堤顶宽固定时，坡度的增加会导致潜堤断面面积的减小。图10给出了顶宽固定，h=0.5 m，H=0.04 m，W=2.8 m，wt=0.3 m，wh= 0.25 m时，不同潜堤坡度条件下反射系数KR随kh值的变化曲线(分别对应5、8、10工况)。从图10中可以看出：潜堤坡度的增大使得主、次频反射点向kh增大方向移动，同时主频反射系数峰值降低；由于潜堤顶宽固定，坡度的增大使得潜堤断面面积减小，防护效果也随之降低，主频共振反射发生时波长与2倍中心间距之比更接近1。

图11给出了潜堤底宽固定，h=0.5 m，H=0.04 m，W=2.8 m，wb= 0.8 m，wh= 0.25 m时，不同潜堤坡度条件下反射系数KR随kh值的变化曲线(分别对应5、11、12、13工况)。此时潜堤坡度的增加会导致潜堤断面面积的增加。从图11中可以看出：主频共振反射点的横坐标位置没有变化；当坡度δk=5:8时(断面形状退化为三角形)，主频反射系数明显偏低，原因是波浪能量主要集中在水体表面，潜堤靠近水体表面部分面积偏小，无法对波浪形成有效影响；对于其余三种坡度工况，主频反射系数略有增加，但是次频反射系数减小。

3.7 流场分析

本节以h=0.5 m，H=0.06 m，W=2.3 m，wb= 0.8，wh= 0.25 m，δk=1∶1工况组为例，分析共振反射时潜堤周围的流场特性。图12给出了该组工况下kh=0.65时一个周期内的流场图。从图12中可以看到：t=0时一个波浪到达潜堤，波峰处水质点速度较大(见图12-a)；t=0.25T时潜堤的存在使得堤前速度迅速加大，但堤内及附近水质点仍保持较低流速(见图12-b)；t=0.5T时随着波浪传播，潜堤上方波面明显抬升，但水质点速度有所减小，同时观察到堤后的水质点速度已经变小(见图12-c)；t= 0.75T时波峰传播至堤间，第二排潜堤的存在使得水质点速度又有小幅度增加(见图12-d)；t=T时流场进入下一个周期循环(见图12-e)。整个过程中，潜堤内部的水质点速度有所变化，但速度值一直较小；波峰在经过潜堤的过程中，水质点速度有明显的增大—减小—小幅增加—再减小的变化趋势，潜堤后方水域水质点速度较小，说明双排多孔潜堤可以较好地反射入射波能量，提供有效掩护。

12-e t=T注：h=0.5 m, H=0.06 m, W=2.3 m,wb = 0.8 m, wh = 0.25 m, δk=1:1,kh=0.65图12 不同时刻潜堤周围的流场图Fig.12 Flow field diagram around the breakwaters at different times

4 结论

本文基于δ-SPH模型建立了数值波浪水槽，模拟了波浪与多孔介质潜堤相互作用的过程。数值模拟结果和物理模型试验结果符合良好，表明该模型能有效模拟多孔潜堤的共振反射问题，可作为工程设计的有效参考手段。通过改变波浪参数和多孔潜堤参数，数值分析了波浪通过多孔潜堤时的Bragg共振反射现象及其影响因素，研究发现：(1)当入射波长约等于2倍潜堤中心间距时，双排多孔潜堤发生主频反射；(2)波浪未破碎情况下，入射波高变化对反射系数影响很小；(3)潜堤高度增大或水深减小会增加潜堤的反射系数；(4)潜堤中心间距的增加会使主频反射系数增大，但有效作用的波长范围减小；(5)矩形潜堤宽度增大时，主频反射系数随之增大，次频反射系数随之减小，主频反射对应的波浪频率减小；(6)梯形潜堤顶宽固定时，坡度增大会降低主频反射系数，而底宽固定时，坡度增大主频反射系数会增大。