飞行器控制的伪线性系统方法——第一部分：综述与问题

段广仁

(哈尔滨工业大学控制理论与制导技术研究中心，哈尔滨 150001)

0 引 言

控制科学的核心目标是设计出稳定且具有良好性能的闭环控制系统。长期以来，控制科学家们基于对不同控制系统的结构性质和运动规律的深刻认识，提出了多种控制系统设计方法。这些方法所适用的系统从线性系统到非线性系统，从单输入单输出系统到多输入多输出系统，极大地推动了科学技术的进步。

线性系统作为最简单、最基本的一类动态系统，是系统控制理论中发展最成熟、应用最广泛的一个组成分支。线性系统的控制设计分为基于古典控制理论的设计和基于现代线性系统理论的设计两大部分。基于古典控制理论的设计以Laplace变换和复变函数理论为主要数学工具，以传递函数为基本数学模型，以频域响应法为主要研究方法，主要针对单变量线性定常系统进行分析与综合。基于现代线性系统理论的设计以现代数学为主要工具，通过在时域内建立系统模型的状态空间描述，并在此基础上设计出期望的控制律。典型的设计方法包括极点配置[1-3]，特征结构配置[4-6]以及基于Riccati方程的线性二次型最优控制[7-8]等。

自然界或工程实际中的许多系统都是非线性的。例如，航天器制导与控制系统、机器人系统、电力系统等。早在19世纪初期，人们的研究侧重在线性系统上，而对于非线性控制方面的研究也只有简单的相平面分析方法。直到19世纪末期，人们开始逐步针对不同类型的非线性系统提出了不同的方法。总体来说，关于非线性控制[9-22]设计的方法可以归纳为三大类(如图1所示)。

图1 非线性系统控制设计Fig.1 Control design of nonlinear system

1)基于李雅普诺夫泛函的设计方法

1892年，俄国著名科学家李雅普诺夫完成了他的博士论文：《论运动稳定性的一般问题》，奠定了控制系统的稳定性理论，也为非线性系统设计提供了一般性的理论方法，即李雅普诺夫第二方法。这类方法的基本思想是通过寻找一个李雅普诺夫泛函，即一种广义的“能量”函数来度量系统非线性部分的动态，设计控制器使被控系统“耗散”到给定的目标状态。李雅普诺夫方法是一种根本性的基础设计方法。随着时间的推演，人们针对更加具体的系统类别又提出了相应李雅普诺夫泛函的求取方法，从而在这一方向上产生了一些新方法。从考虑匹配条件的滑模控制[14,23-24]，到约束条件更为宽松的反步法[15,25-26]，再到利用开环系统的无源性的无源化方法[16,27]，这些都构成了非线性控制发展史上的里程碑式的结果。

2)最优控制方法

最优控制是通过权衡系统状态和输入来设计系统的控制器，使闭环系统的某种性能指标达到最小。关于非线性最优控制理论的研究可以追溯到20世纪50、60年代，通过离散的Bellman动态规划方法将离散最优控制问题转化为HJB (Hamilton-Jacobi-Bellman)方程的求解问题[28-29]。到了20世纪中叶，出现了著名的Pontryagin极大值原理，可以把一般的连续非线性控制问题转化为HJB方程的两点边值问题进行求解[30-31]。在这一方向上，针对不同的系统形式和指标形式，后期又涌现出了一批新方法，如H∞控制[17,32]和预测控制[18,33]等。线性二次型最优控制是Pontryagin极大值原理在线性系统框架下的完美呈现。作为线性二次型最优控制的一种直接推广，人们又进一步提出了基于状态依赖Riccati方程的方法[34]来解决非线性二次型最优控制问题。

3)以线性主导的设计方法

人们对于线性系统的认识是比较深入和完备的，线性系统的许多特性也是最为人们所青睐的。因此，人们自然希望利用线性系统来研究非线性系统，或者说尽量把非线性系统的控制问题归结为线性系统的控制问题。出于这种考虑，历史上产生了两种自然的思想。

一种是求取非线性系统的一个控制器，使得闭环系统成为线性系统，这就是所谓的反馈线性化方法。一旦一个非线性系统能反馈线性化，则线性系统理论和方法就可以直接使用，反馈线性化方法是20世纪70年代的代表性成果[35]。后期发展的微分几何方法的一个主要优点也在于反馈线性化[36]。从控制系统的结构出发，利用已有的微分几何及微分代数方法，将线性系统已有的成果通过用流形代替线性空间的方式推广到非线性系统上，同时也考虑如何在一定条件下将“复杂”的非线性控制系统通过非线性变换转化为某种意义下等价的线性控制系统。

另一类设计思路是用线性系统来逼近非线性系统的方法。增益调度方法和模糊T-S方法是这方面的典型代表。增益调度方法将线性化方法的有效性扩展到若干个工作点，针对每个工作点设计线性反馈控制器[22,37]。模糊T-S方法利用T-S模糊规则将非线性系统描述为若干个线性子系统的动态线性组合进行控制器设计[38]。

下节中将在上述非线性控制系统设计方法分划的框架下对飞行器的非线性控制方法给出一个概述，并由此引出伪线性系统的概念。接下来的两节则分别给出了卫星姿态与轨道控制和飞行器制导与控制中典型飞行器控制问题的一般伪线性系统模型描述。有关伪线性系统控制的直接参数化方法将在该文的第二部分中继续讨论。

1 飞行器控制方法

航空航天技术是21世纪以来发展最迅速、对人类社会最有影响力的尖端科学技术领域之一。飞行器是航空航天活动的重要载体，也是航空航天技术的核心组成部分。飞行控制技术作为飞行器的灵魂，是实现飞行器安全、稳定飞行的重要保障，对飞行器系统设计有着举足轻重的作用。飞行器可以粗略分为航空飞行器(如导弹)、航天飞行器(如卫星)以及临近空间飞行器三大类。虽然不同类别的飞行器所处飞行环境以及动力学特性大相径庭，但从控制设计角度来看，它们都是典型的具有多变量、多通道耦合、不确定、受干扰等特点的非线性被控对象，所追求的目标也都是速度快、精度高、准确、稳定又具良好机动性[39]。随着控制理论的蓬勃发展与飞行器控制研究的不断深入，当前有关非线性系统的各种控制设计方法几乎均被尝试应用于飞行器控制系统设计中，内容遍及古典控制、现代控制、时域方法、频域方法、鲁棒控制、自适应控制、预测控制、智能控制等诸多范围[40-57]。本节从方法论的角度对飞行器控制方法做一简单概述。

1.1 基于李雅普诺夫泛函的飞行器控制方法

常用的基于李雅普诺夫泛函的飞行器控制设计方法包括滑模变结构控制方法和反步法。滑模控制方法具有响应快、算法简单、对于模型参数和外界扰动不灵敏等优点，被广泛应用于飞行器控制领域。文献[58-61]基于滑模控制方法研究了卫星姿态控制，文献[62]将滑模控制方法应用于航天器自主交会对接问题。文献[63-65]利用滑模控制方法研究了导弹导引律控制设计问题，文献[66-68]和文献[69-70]分别将滑模控制方法应用于具有强不确定性的高超声速飞行器控制和导弹制导控制一体化设计中。

相比于滑模变结构控制，反步法的最大优势是可以有效地处理非匹配不确定性。基于反步法的飞行器控制设计利用飞行器系统模型所固有的级联结构，通过灵活选用李雅普诺夫函数结合递推方法设计控制律。文献[71]将反步法与鲁棒自适应控制相结合，研究了导弹自动驾驶仪的控制设计。文献[72]和[73]等则将反步法与滑模控制相结合设计航天器姿态跟踪控制算法。文献[74]结合干扰观测器和反步法研究了存在饱和与测量不确定性情形下的航天器姿态镇定控制律设计问题。考虑到标准反步法存在“级数膨胀”的缺陷，一些改进的反步法也被应用于飞行器控制中。文献[75-76]结合动态面控制技术实现了导弹制导控制一体化设计，文献[77]利用指令滤波反步法设计了三通道飞行器控制系统。近年来，随着研究不断深入，一些特殊形式的李雅普诺夫函数也被引入到基于反步法的飞行器控制设计中。文献[78]利用基于障碍李雅普诺夫函数的反步法研究了考虑状态约束的航天器自主交会姿轨控制问题。文献[79]利用基于积分形式的强李雅普诺夫函数的反步法设计了具有有限时间收敛特性的航天器姿态跟踪控制算法。

1.2 基于优化的飞行器控制方法

最优控制是现代控制理论中较成熟的一个分支，最优控制在飞行器控制方面具有很强的应用背景，典型的如燃料最省控制、最优调姿规律、最优制导律等[80]。基于优化的控制设计方法也被广泛应用于飞行器制导控制律设计以及航天器控制中，如文献[81]针对机动目标制导律问题设计了基于跳变系统的最优制导律，文献[82]和[83]分别提出基于线性二次型和预测控制的最优制导律设计方法。文献[84-87]则利用不同优化控制方法研究了航天器姿态控制问题。考虑到飞行器动力学模型通常呈现出较强的非线性，因此，近年来基于优化的飞行器控制设计大多集中于非线性最优控制方面。众所周知，求解非线性最优控制问题的最大障碍在于HJB方程很难求得解析解。为了克服这个困难，两种有效的数值解法被提出，一种是状态依赖Riccati方程(State dependent riccati equation, SDRE)方法，另一种是θ-D方法。前者通过实时地求解一类代数Riccati方程得到局部渐近稳定的次优反馈控制律，后者通过一种摄动方法给出了HJB方程的一个数值解，并利用该数值解可以构造一类反馈次优控制律。由于该数值解不必实时求取，从而极大地降低了求解的复杂性。Stansbery等[88]和Vaddi等[89]分别应用SDRE方法设计了航天器的姿轨联合控制律和导弹导引控制一体化控制律。Xin等[90-91]学者将θ-D技术应用于多种飞行器优化控制律设计中。

1.3 基于线性主导的飞行器控制方法

前文已经提及，线性系统的控制设计相对于非线性系统来说要简单得多，且人们对于线性系统理解更为深刻，因此，在进行飞行器控制设计时也自然会考虑采用基于线性系统理论的设计方法。常见的基于线性主导的飞行器控制设计分为两类，一类是基于近似线性化模型的设计，另一类是基于精确线性化模型的设计。

基于近似线性化模型设计的基本思路是,首先根据设计要求确定若干个特征点，并将飞行器模型于各个特征点处线性化，得到若干个局部线性化模型；然后利用局部线性化模型，结合古典或现代控制理论(如古典的根轨迹法、频域设计法，现代的线性最优控制、H∞与μ综合，鲁棒参数化方法等)设计各特征点处的局部控制器；最后通过拟合各个局部控制器的切换规律完成整体系统的控制器设计。这种设计方法现已相当成熟，并已被许多实际飞行试验证明是非常有效的，相关工作可见文献[92-98]。但是需要指出的是，该方法是建立在系统慢时变这一假设之上的，同时难以从理论上严格保证闭环系统全局稳定性，因此，基于该方法所设计的控制器也难以从根本上绝对保证飞行的安全性。

基于精确线性化模型的设计是首先利用反馈线性化技术或者动态逆技术将飞行器原始非线性模型转化为线性形式，进而应用熟知的线性系统控制方法进行控制器设计。与近似线性化方法相比，它不会产生模型精度损失[99]，因而受到控制科学家和工程师的广泛关注，也被应用于飞行器控制设计中，如文献[100-101]分别利用反馈线性化和动态逆方法研究导弹控制系统设计，文献[102]结合反馈线性化方法和干扰观测器设计了高超声速飞行器纵向控制系统，文献[103-104]将反馈线性化技术应用于航天器姿态控制中。虽然反馈线性化方法在非线性控制领域显示了巨大的优越性，然而，由于它依赖于精确的对象模型，因此其在飞行器控制中的应用受到了一定程度上的限制。

随着航空航天技术的飞速发展，现代飞行器具有多任务、多工作模式、大范围高速机动等特点。这种新型飞行器以宽广的飞行包络、极高的飞行速度、超强的机动性和灵活的敏捷性为基本特征，其动力学特性表现为复杂的快时变、多变量强耦合、严重不确定性和强非线性。飞行器的控制系统设计面临着更精确、更灵活而又更可靠的多方面要求，这也从根本上限制了一些经典设计方法的使用。从发展角度看，现代飞行控制设计面临着前所未有的困难和挑战，其理论和方法亟需进一步完善、创新和发展[105-108]。

1.4 伪线性系统控制方法

上文阐述了非线性控制系统的“以线性为主导的设计方法”。试想，如果我们能在形式上将非线性系统表为线性系统，然后利用线性系统的一些设计思想来设计控制律，在某些情况下是否可以得到一些更好的结果呢？

这类形似线性系统实则非线性系统的系统便称为伪线性系统。在过去的十年中，我们把线性系统参数化设计方面的工作推广到伪线性系统，为伪线性系统的研究打开了一个广阔的空间，也为很多飞行器控制问题，如卫星姿态控制、空间交会与拦截、飞行器姿态控制以及飞行器制导等，提供了一条简单、有效的途径[109-114]。

本文的目的就是介绍飞行器控制的伪线性系统方法。下一节将一些典型的飞行器控制问题转化为伪线性系统问题，然后在该文的第二部分给出一般伪线性系统控制的直接参数化设计方法。

2 卫星姿轨控制问题

根据刚体动量矩定理可知，卫星的姿态动力学模型在惯性坐标系中可以表述为

(1)

式中

(2)

分别是卫星的惯量矩阵和角速度，

(3)

分别是控制力矩、重力梯度力矩和干扰力矩。动力学方程(1)也可写为如下分量形式：

(4)

2.1 卫星姿态控制问题

采用欧拉角描述卫星姿态具有更直接、更明显的几何意义。

2.1.1基于欧拉角的描述

采用欧拉角φ,ϑ和ψ描述卫星姿态，描述方式与坐标系的旋转方式有关。当采用Z(ψ)→Z(φ)→Z(ϑ)的旋转顺序时，卫星的角速度在惯性坐标系中的表达式为

(5)

另外，式(1)中的重力梯度力矩Tg可根据下述公式得到

(6)

对方程(5)两端求导，可得卫星的角加速度关于欧拉角的表达式。将角速度表达式(5)、重力梯度力矩表达式(6)以及获得的角加速度表达式代入式(1)，经过整理，可得关于欧拉角的一组二阶微分方程组。为了表达方便，我们引入如下一组π函数

(7)

(8)

(9)

则可以将得到的二阶微分方程表述为二阶伪线性系统的形式。

命题1[109]. 定义干扰向量Td如式(3)所示，状态变量为

则描述卫星姿态运动的方程(4)～(6)可以转化为如下二阶矩阵形式

(10)

其中

这里，

上述中的π函数由式(7)～(9)给出。

2.1.2基于四元数的描述

采用四元数描述卫星姿态，卫星的姿态运动学模型在惯性坐标系中的表达式为

(11)

其中

(12)

这里，

式中

对方程(11)两端求导，可以得到卫星的四元数关于角速度和角加速度的表达式

(13)

在式(11)两边同时左乘ET(Q)，并利用关系ET(Q)E(Q)=I3，经过整理，可以得到角速度ω关于四元数的表达式

(14)

其中

(15)

这里，

(16)

(17)

其中

(18)

这里，

另一方面，重力梯度力Tg可根据下式得到

式中:C3是旋转矩阵的第三列向量，表达为

(19)

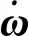
命题2[110]. 定义状态变量q、转动惯量J及控制变量u如式(12)和(1)～(2)，那么基于四元数描述的姿态运动方程(1)和(11)可以转化为如下二阶矩阵形式

(20)

其中

(21)

(22)

(23)

2.2 空间交会与拦截问题

2.2.1空间合作交会问题

图2 合作航天器交会系统Fig.2 Cooperative spacecraft rendezvous

为从追踪航天器到目标的向量在该坐标系中的表示，其中，xr,yr和zr为相对位置变量。

假设所考虑的追踪航天器和目标航天器均为刚体，并且仅受重力和各自的推力影响。定义ac是由追踪航天器推进装置的推力产生的加速度，at是由目标航天器推进装置的推力产生的加速度，则航天器相对轨道动力学模型可由如下二阶微分方程表示：

ac-at

(24)

式中:μ是地球引力常数，R为目标航天器的轨道半径，

(25)

下述命题将得到的二阶微分方程(24)表述为伪线性系统的形式。

命题3[111]. 定义状态变量和控制变量为

则描述合作航天器交会问题的方程(24)可转化为如下的二阶矩阵形式

(26)

其中

2.2.2空间非合作交会与拦截问题

假设所考虑的航天器均为刚体，只受重力和主动脉冲的作用，且不考虑自旋、绕太阳旋转等因素的影响。令Rch为从地球中心到追踪航天器的矢量，|Rch|为Rch的模，ach为追踪航天器产生的加速度；Rta为从地球中心到目标航天器的矢量，记|Rta|为Rta的模，ata为目标航天器产生的加速度。设r=Rta-Rch为从追踪航天器到目标航天器的向量，根据二体问题，两个航天器之间的相对运动在地心惯性坐标系OIXIYIZI(ECI)中可描述为

(27)

式中:μ是地球引力常数。

(28)

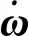
对于交会和拦截问题，人们普遍承认|Rch|≫|r|，因此有

(29)

将式(27)代入式(28)，并结合式(29)，可得

(30)

其中，倾斜角ε为xl与xl到XI-ZI平面的投影之间形成的夹角，偏航角β为xI与xl到XI-ZI平面的投影形成的夹角，且ε和β均可测，

这里Rx,Ry和Rz为Rch的分量。

命题4[112]. 定义

则在LOS坐标系中的航天器交会问题的相对运动方程(30)可改写为二阶矩阵形式：

(31)

其中

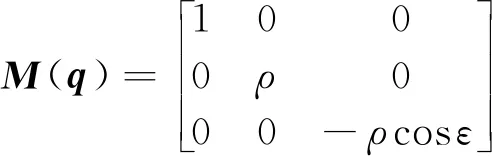
在拦截问题中,不考虑变量ρ，只考虑角度β和ε。

命题5[112]. 定义

则卫星拦截模型可转化为如下二阶矩阵模型

(32)

其中

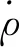
3 飞行器制导与控制问题

3.1 飞行器姿态控制问题

导弹的姿态动力学模型在惯性坐标系中可以表述为式(1)。但在本小节中我们考虑重力梯度力矩Tg=0的情形。

另一方面，导弹的姿态运动学模型可以表示如下[57]

(33)

式中:ϑ,ψ,γ分别是导弹的俯仰角，偏航角和滚转角，用以表示导弹的相应姿态，其余符号物理意义与式(1)相同。

欧拉角(ϑ,ψ,γ)经常被用于定义导弹在地球坐标系下的姿态，而导弹本体坐标系是固定在导弹之上随着导弹运动。地球坐标系和导弹本体坐标系之间具有以下转换关系[80]

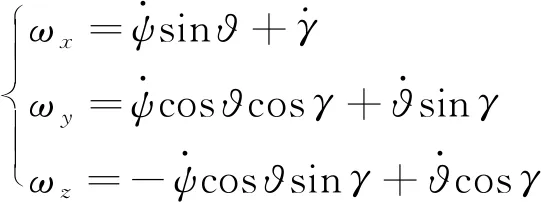
(34)

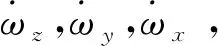
(35)

命题6[113]. 如式(1)定义向量u，同时定义状态变量为

(36)

则描述导弹姿态运动的方程(1)和(33)可以转化为如下二阶矩阵形式

(37)

其中

(38)

(39)

(40)

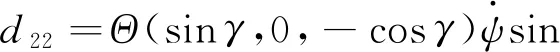
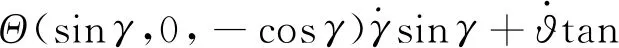
(41)

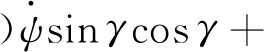
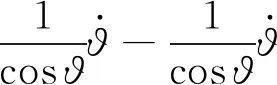
(42)

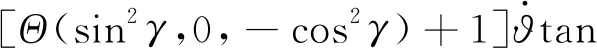
(43)

其中

Θ0(ϑ,γ)=Θ(sin2γsin2ϑ,cos2ϑcos 2γ,

-cos2γsin2ϑ)

(44)

上述中的Θ函数由式(35)给出。

由式(38)可见，只要俯仰角ϑ不达到π/2，矩阵B(x)便是有限的。

3.2 飞行器制导问题

如图3所示，考虑导弹和目标的相对运动问题。假设目标是一艘军舰，因此其在垂直方向上不存在相对运动，而只在水平面上进行机动。

图3 导弹-目标几何关系Fig.3 Missile-target engagement geometry

O-xyz是地面参考坐标系。M,T和MT分别表示导弹、目标和导弹-目标视线，r表示导弹和目标的距离，qθ和qφ分别是MT的倾角和方位角，Vt表示目标的速度，φt表示Vt的方位角。需要说明的是，由于假设目标始终在水平面运动，所以Vt的倾角等于零。相应地，Vm表示导弹的速度，θm和φm分别表示Vm的倾角和方位角。

引入如下的变量

(45)

则图3中所示的导弹-目标相对运动方程可以表示为[65]

(46)

另外，导弹的质心动力学模型可以表示为

(47)

式中:u1和u2分别表示导弹加速度沿着航迹坐标系在Oy轴和Oz轴的分量。

考虑到此问题的物理意义，为了实现有效的制导，需要提出以下必要合理的假设：

假设1.Vm>Vt，且πr对于取值范围内所有的qθ,qφ,φm和θm都不为零。

对式(46)中的第二个和第三个方程的两端分别进行求导，并将式(45)和(47)代入求导后的结果，再结合式(46)中的第一个方程，经过整理可得一组二阶微分方程组，从而可得导弹制导模型的伪线性系统形式。

命题7[114]. 定义状态变量和控制变量为

(48)

则导弹制导模型(46)和(47)可以转化为如下二阶矩阵形式

(49)

其中

(50)

B(x)=

(51)

(52)

(53)

这里

Vmcosθmcos(qφ-φm)

(54)

说明1. 式(45)中的at1和at2具有明确的物理意义，代表目标机动加速投影，详见文献[114]。

4 结束语

飞行器控制问题本质上都是非线性的，只有在极特殊的情况下才能按线性情况来处理。

尽管非线性控制方法很多，但在稳定性这一重要问题上都给出了比较苛刻的条件。这也导致了飞行器的许多非线性控制方法不是十分令人满意。

虽然飞行器控制问题多种多样，本文却展示了它们的一个公共特性，即它们的模型都可以表述为一类二阶伪线性系统形式。如果针对这种一般的二阶伪线性系统存在非常简单、方便、有效的控制方法，那么许多飞行器控制问题便得到圆满解决。该文的第二部分将介绍一般二阶伪线性系统的一种直接参数化设计方法。这种直接方法比起基于一阶状态空间模型的设计方法显示了极大的优越性。

致谢

作者感谢其学生章智凯、赵琴、胡艳梅、黄秀韦等人协助查找文献和组织材料。