在数据分析中培育学生统计推理能力

朱荣武

摘    要     统计推理是个体适应信息社会的必备思维能力，需要从小学阶段就结合统计与概率教学进行渗透。在教学过程中要突出过程性、方法性和体验性，关键是紧扣描述数据分析和推断数据分析两条主线，引领学生经历数据分析及其应用过程，在具体的思维活动中发展他们的数据意识、随机思维及审慎的态度。

关键词   统计推理 描述数据分析 推断数据分析 随机思维 审慎的态度

统计推理，就是利用统计数据或统计信息进行的推理[1]，其本质是一种归纳推理，前提是一定数量的统计数据，过程是发现并提炼数据中蕴含的信息并依据这些信息做推断或决策。统计推理是个体适应信息社会必备的思维能力，在小学阶段渗透培育，有利于学生体会统计推理的特点，掌握简单的统计推理方法，学会用随机思维看待客观事物及其规律，实现思维的“更清晰、更深入、更全面、更合理”[2]，并形成尊重事实、用数据说话的态度。

立足小学数学课堂培育统计推理能力，关键是引领数据分析及其应用过程，要紧扣两条主线——描述数据分析和推断数据分析[3]，既让学生学会从“一堆杂乱无章的数据中提炼信息、寻找规律”[4]，也让学生经历简单的从样本推断总体的过程，不断地体会数据分析方法、体验数据价值、理解亲近数据、积累随机思维经验。但日常统计与概率的教学往往只注重显性的统计、概率知识的教学，弱化了统计推理能力的培育，因此结合日常教学有意识、有预见地渗透统计推理能力的培育，任务迫切。

一、经历描述数据分析过程，感受数据中的信息

统计学的研究基础是数据，但统计推理依靠的不是数据本身而是数据中的信息。描述数据分析是不考虑数据随机性、只针对调查数据本身的一种数据分析形式[3]。结合学生的认知经验，有层次地引领描述数据分析过程，从数据中提炼信息、发现规律、感受数据与信息的关系，是培育统计推理能力的基础。

1.理解表达数据本身的信息

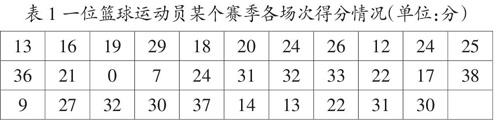
数据是信息的载体，通过问题引导学生表达对数据本身含义的理解，提炼信息，产生对数据的亲近感，是体验数据与信息关系的教学起点。比如呈现调查数据（表1），先让学生说说对每个数据含义的理解，明白调查的内容和侧重点。接着让学生围绕以下问题展开讨论：最高得分是多少？最低呢？相差多少分？得分在20以上的有多少场？得分在30以上的呢？这里既涉及到极值、极差，也涉及到数据的简单分布，让学生在思考表达中切实感受到数据中是有信息的。

2.比较提炼数据间的关联信息

基于同一事件的调查数据总是有联系的，引领学生用联系的眼光观察、比较数据，寻找数据间的关联信息，是深入理解数据与信息的重要内容。比如引导学生根据自己一至五年级每年体检的身高数据，思考从一年级到五年级自己长高了多少、从几年级到几年级身高增长最快等问题。学生基于数据的比较、计算，能超越数据本身得到更多的发现。再比如呈现“李明记录了自家7袋蒜头的重量——28千克、31千克、31千克、29千克、33千克、32千克、30千克”，引导学生思考：比较每袋的重量，你能想到什么？学生会根据数据间的关系提炼“每袋都差不多重、每袋大约重30千克”等关键信息。当然有时数据间的关联信息也体现在样本与样本、样本与總体之间。

3.发现概括数据背后的信息

数据背后的信息在这里指数据中蕴含的事实或规律。比如引导学生分组统计、整理同学一庹长度和身高的数据并展开比较，鼓励他们说出自己的发现：一个人的一庹长度与身高有联系，身高特别高一庹就特别长，身高比较矮一庹就比较短等。有趣的规律让学生对数据蕴藏的信息有了鲜活的体验。

二、经历推断数据分析过程，丰富和发展随机思维

随机思维是构成统计推理能力的重要内核，引领学生结合实际情境经历推断数据分析过程，发展随机思维，是培育统计推理能力的核心。推断数据分析强调通过已调查数据去推断调查数据之外的信息，通常表现为通过样本推断总体[3]。由于数据本身具有随机性，推断的思维基础也是合情推理，因而推断的结论具有随机性。

1.比较不同范围的数据，初步感受样本和总体

尽管小学生很难理解样本和总体的概念，但仍可用简单的模型通过比较不同范围内的数据，获得初步感受，从而奠定随机思维的概念基础。比如在研究“全班同学中哪个月出生的人数最多（少）”时，引导学生将本小组的数据（样本）和其他小组（样本）以及全班汇总的数据（总体）展开比较并说出自己的发现，学生既会发现样本与样本、样本与总体间的相似性，也会发现其不同点。接着引导思考“如果在全校学生中调查，又会怎样？”促使学生将本班数据作为一个样本去和全校数据这一新的总体比较。多层次的比较不断强化了学生对样本和总体概念的感受。

2.分析数据背景，体验数据的随机性

数学课程标准强调，体验随机性包括两个方面：一是对同样的事情每次收集到的数据可能不同，二是只要有足够的数据就可能从中发现规律。教学中可以引导学生结合数据背景来反思体验。比如在研究“上学时间”时，先布置学生连续记录自己两周内每天上学途中所花时间，然后组织思考：为什么路程相同，每天所花的时间却不一样？从连续记录的时间里你能发现什么？通过反思明白：受交通路况、天气等因素影响，每天的上学时间不可能是完全一样的，所以每次收集到的数据肯定会有所差别。但排除相差较大的时间后，剩下的数据都在一定范围内波动，是有规律的，所以能估计出自己每天上学的大约时间。对数据随机性情理上的认同为发展随机思维奠定了基础。

3.用数据说话，体验推断结论的随机性

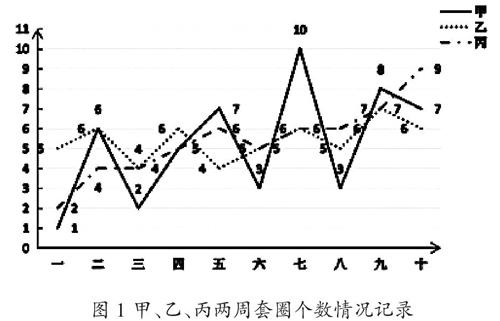
根据同一变量已有的数据预测未来发展趋势，不同的人、不同的分析方法会得到不同的结论，这些结论无所谓对错。引导学生用数据做推断并体验结论的多样性和不确定性，有利于学生随机思维经验的积累。比如以“派谁去比赛”为话题引导学生用数据说话。

生1：我选甲，最高成绩是甲创造的。

生2：甲不稳定，我选乙。

生3：我选甲，尽管乙比较稳定但成绩一直平平，如果对手很强，他就很难取胜。

生4：我选丙，丙的成绩后来一直在提升，说不定比赛时会继续提升呢！

师：真是各说各有理，老师也不好决定了。经过讨论你们有什么收获呢？

生5：根据数据和折线图可以帮助我们做判断。

生6：虽然大家的意见不同，但我觉得都有道理，因为都是数据在指导我们。

生7：无论选谁去都不一定确保获胜。

……

有理有据的辩论、不确定的结论，以及深刻鲜活的反思过程，让随机性熠熠生辉。

4.展开概率分析，拓宽随机思维视野

描述随机现象的数学方法有两个，一是统计，二是概率。概率分析方法一般有两种：一种是根据“所有可能的结果”去判断某种结果出现的可能性;一种是通过重复试验，由事件的频率估计概率。比如研究“从3张红桃和1张黑桃中任意摸1张，哪种牌被摸到的可能性大？”这一事件。先引导学生列举出所有可能的结果再判断：可能的结果有4种，其中3种是红桃，1种是黑桃，所以摸出红桃的可能性大。接着组织试验——从中任意摸出1张，摸后放回，打乱后继续摸，一共摸40次并记录每次摸到的花色。试验的结果无外乎三种：红桃多（大多数）、一样多和黑桃多（个别）。然后组织学生交流讨论：统计结果能说明之前的判断吗？通过数据分析，学生发现统计结果有的能证实之前的判断，有的则不能，进而引导学生体会：通过概率分析既可以事先对结果进行合理预测，而实际结果大多符合规律，但也有例外，例外的个案并不能否定规律。

三、经历数据分析应用过程，体验统计推理的价值

应用数据分析解决实际问题，既要关注问题的现实性和趣味性，又要突出数据分析方法与问题解决之间的关联，还要着力提高学生思维的卷入程度、水平及其感受体验。

1.统计分析提炼规律

围绕要解决的问题整理调查数据、展开数据分析、提炼信息发现规律，是解决实际问题的重要方式。在小学生的生活世界中这样的实例也有很多，教学中要引领学生经历解决问题的全过程。比如解决“运动与脉搏有怎样的关系？”这一问题，先组织学生讨论制订方案：四人为一组分别测出3项1分钟脉搏的次数——运动前的脉搏次数、原地高抬腿30秒后的脉搏次数、休息2分钟后的脉搏次数，算出平均数，并比较研究。然后展开实验—统计数据—比较分析—提炼规律—获得结论—反思感悟等活动。其间方案的酝酿是重点，有利于学生从整体上了解用统计推理解决问题的过程特点;反思感悟是关键，既强化了方法体会还获得了统计推理的价值体验。

2.抽样分析推断总体

通過“由样本推断总体”解决问题，不仅要重视结果的获得还要不断引发深度思考。比如解决“班级里的男（女）同学中穿多少码鞋的人数最多？”这一问题，先让学生理出思路：将男女生分别分成若干组，整理出每组中穿各种鞋码的人数，利用小组数据去估计全班情况;再分别汇总全班男女生的数据，做出判断。活动中要不断引发思考：你觉得其他组的调查数据会和你们组一样吗？怎样判断全班的情况？你们小组数据与全班数据有什么关系？引导学生体会：各男、女生小组数据（样本）间既有相似性也有区别，可以根据小组的特点去估计全班（总体）的特征。接着引申思考：你觉得三年级其他班的情况会怎样？整个三年级呢？让学生体会随机数据中的规律，即三年级的学生年龄都差不多，穿鞋码数的情况也会和本班大致相同。再追问：六年级的情况会和咱班一样吗？让学生体会用三年级学生的情况去推测六年级显然不合理，体会不同范围内统计数据和结论的随机性。

此外，培育统计推理能力还要着力培养学生以审慎的态度评价统计推理活动的意识，即养成一种审视统计推理过程的理性自觉。因为统计推理尽管是基于数据说话，但由于其不是必然性推理，结论并不一定正确。比如提供以下信息让学生展开推理：三年级学生的近视人数比去年增加40%;六年级学生的近视人数比去年增加20%;哪个年级学生的视力情况好些？绝大多数同学认为六年级学生的视力情况好于三年级。此时教师不动声色地呈现：三年级去年近视10人，六年级去年近视100人。学生恍然大悟：在没有基数的情况下比较百分率是没有意义的;根据数据做判断要小心，不能盲目…… 教学中要有意识地让学生经历分析—推断—反思—修正的过程，在积累思维经验的同时形成科学的态度。

参考文献

[1] 邵光华.作为教育任务的数学思想与方法[M].上海：上海教育出版社，2009.

[2] 郑毓信.以“深度教学”落实数学核心素养[J].小学数学教师，2017（09）.

[3] 史宁中.基本概念与运算法则：小学数学教学中的核心问题[M].北京：高等教育出版社，2013.

[4] 史宁中.统计的基本思想与方法及其课程教学设计[J].课程·教材·教法，2005（06）.

[责任编辑：陈国庆]