考虑充电等待成本的电动汽车路径问题

李默涵，毛李帆，郑从镇，石进永，汪映辉

(1.海南电网有限责任公司，海南 海口 570100；2.国电南瑞科技股份有限公司，江苏 南京 211106)

在空气污染和能源短缺的双重压力下，电动汽车作为代替燃油车的交通工具应运而生。近年来，国家出台了大量优惠政策，电动汽车得以迅速发展，一些物流公司也开始使用电动汽车来进行货物配送服务，而配送时选择合适的行驶路线可以有效降低配送成本[1]。1959年，Dantzing和Ramser首次提出车辆路径问题(vehicle routing problem，VRP)的概念——通过设计车辆行驶路线来完成在配送中心和客户之间运输货物的目的，同时追求行程短、耗时少、成本低等目标。1988年，Solomon通过在基础VRP模型中添加时间窗约束，首次构建了带时间窗的车辆路径问题(vehicle routing problem with time windows，VRPTW)模型[2]。随着电动汽车的快速发展，电动汽车的路径问题随之而生。相较于燃油车的路径问题，电动汽车的路径问题需要考虑电动汽车的电池续航及充电站位置等因素。Jun Yang等人提出了考虑载重量的电动汽车路径问题，采用快速充电且允许多次充电的方式，但未考虑客户服务时间窗[3]。2014年，Schneider等人提出了带时间窗的电动汽车路径问题，添加了时间窗约束条件，要求车辆在规定时间内到达目的地[4]，具有现实意义。近年来，国内外对VRP及其衍生问题进行了研究，提出了许多优秀的解决方案，但现有对电动汽车路径问题的研究均未考虑到充电站对电动汽车的容纳量，即认为充电站的容纳量是无限大的，所有电动汽车到达充电站后都可以立即充电。然而，由于电动汽车保有量日渐增大，充电站内经常会出现排队等待充电的情况，这使得将现有文献的解决方案运用于实际时会出现或大或小的偏差。

为了研究排队等待对路径问题解造成的影响，并完善电动汽车路径问题的解决方案，本文基于现有文献，通过分析时间窗、电动汽车容量、充电站排队时间、充电站位置、电动汽车充电曲线、电池荷电状态(state of charge，SOC)等约束条件，建立考虑充电等待时间的带时间窗的电动汽车路径问题模型，并采用自适应大规模邻域搜索(adaptive large neighborhood search，ALNS)算法对路径问题模型进行求解，最后通过物流电动汽车运行算例验证所提模型的有效性。

1 问题描述

考虑到电动汽车电池容量及充电站位置的约束，在保持时间和能源可行性的同时，需挖掘1套经过所有客户点的行驶路径，同时该路径需要满足充电需求和软时间窗[5]。路径中设有充电站供电动汽车充电，站内假定只配备1台充电设施，因此到达充电站的电动汽车可能需要排队等待充电。客户有服务时间窗的要求：如果电动汽车在客户要求的最早服务时间前到达客户点，就会产生等待时间成本；如果电动汽车晚于客户要求的最晚服务时间到达客户点，则会产生迟到惩罚成本。此外，还需考虑电动汽车的固定购置成本及电动汽车司机的薪酬成本。问题的目标是确定满足所有约束条件的最低成本路线。

假设每个充电站只配有1个充电设施，且电动汽车到达充电站符合平均值为λ的泊松分布。每个充电站都可以作为1个排队系统，电动汽车为排队实体。当电动汽车在充电设施空闲时到达充电站，立即进行充电；如果电动汽车在充电设施工作时到达充电站，则必须等待较早到达充电站的车辆完成充电后，才能进行充电。由于充电站是公共开放的，没有关于队列状态的预先信息，很难确定服务时间分布函数[6-7]；因此，服务时间可以从已知均值和标准差的车辆到达率的分布中提取。由于这是具有泊松到达和一般分布服务时间的单个服务器的情况，符合M/G/1排队系统的特征。

在M/G/1中，字母“M”表示指数分布的无记忆性。由于电动汽车到达充电站符合泊松分布，连续2辆电动汽车到达充电站的间隔时间服从参数为λ的指数分布。服务时间不属于特定的分布情况，字母“G”代表服务时间的一般分布；数字“1”表示排队系统中只有1台服务器。设充电时间为Tc，其均值为E(Tc)，方差为D(Tc)。为了满足系统稳定性，充电器的利用率ρ=λE(Tc)应该小于1。

将时间离散化为一系列时间段，用以处理等待时间问题，即用[tm,tm+1]表示开始和结束时间分别为tm和tm+1的时间段m。由于交通密度会随时间的变化而变化，车辆到达充电站的到达率是一个关于时间的函数，且由于充电站的地理位置不同，各个充电站的到达率也有所不同[8]。在图1中，将1 d分为5个时间段，并且展示了充电站S的车辆到达率分布情况。在现实生活中，车辆到达率如图1中的光滑函数曲线。

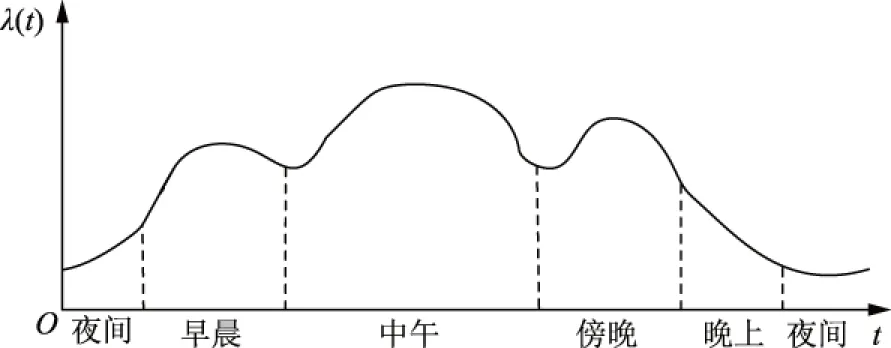
图1 充电站车辆到达率的时间曲线Fig.1 Time curve of charging station vehicle arrival rate

为了方便建立数学模型，将时间离散化并通过分段线性函数来获得近似的车辆到达率曲线，如图2所示。同时，为了保持先进先出的特性，在不同时间段之间加入1个短时间的过渡区，保证较晚到达充电站的车辆不能先于较早到达的车辆离开充电站。

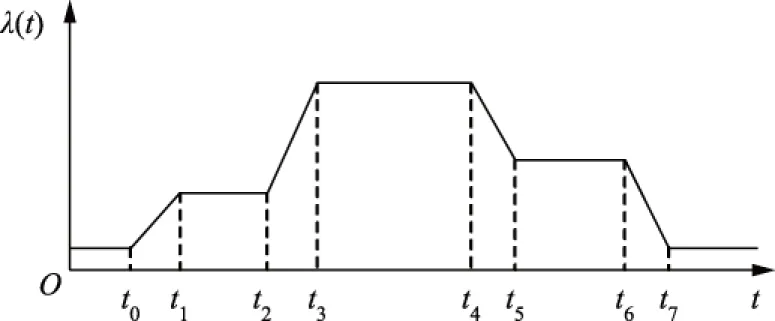
图2 充电站车辆到达率的分段线性近似曲线Fig.2 Piecewise linear approximate curve of charging station vehicle arrival rate

对于t时刻到达充电站S的电动汽车，队列中的期望等待时间E(WS(t))可以用M/G/1排队系统的稳态方程计算，即

(1)

其中

(2)

式中下标S表示充电站。

显然，E(WS(t))在过渡区是非线性的，这里采用线性函数对其进行近似表示[9]，如图3所示。每一段曲线的等待时间由斜率k和截距g表示，如果电动汽车在时间段m内的t时刻到达充电站，则等待时间为g+k(t-tm)。本文假设所有电动汽车均运行于电池SOC为10%～90%的状态下，且充电传输的能量在0～0.8q之间呈均匀分布，其中q为电池容量；因此，期望充电时间E(Tc)=(0.8q×r)/2=0.4q×r，其中r为充电率。同样，服务时间的方差为D(Tc)=(0.8q×r)2/12。

图3 充电站等待时间的分段线性近似曲线Fig.3 Piecewise linear approximate curve of charging station waiting time

2 最小化电动汽车路线成本模型

2.1 电池充电时间函数

电池充电函数是一个非线性的连续凹函数，为了方便建模，采用1个分段线性曲线函数来近似表达充电函数[10]，如图4所示。图4中分段点l对应的时间为tl，al表示电池SOC，其中l∈B={0,…,b}，B为分段点集合。本文假设所有充电站配备相同的充电设备，即所有电动汽车的充电情况均符合近似充电函数。

图4 电池充电过程的分段线性近似曲线Fig.4 Piecewise linear approximate curves in process of battery charging

2.2 问题假设

本文构建模型的目标是使电动汽车行程的总成本最低，为了简化问题，做出以下假设：

a)行驶过程中，电动汽车电量不足时可以进入充电站充电；

b)每个充电站只有1台充电设施，电动汽车进入充电站充电可能需要排队等待；

c)每个客户都有服务时间窗，电动汽车可以在时间窗外到达客户点，但早于客户要求的最早服务时间到达服务点会产生等待成本，晚于客户要求的最晚服务时间到达客户点会产生超时惩罚成本[11]；

d)车辆行驶终点具有时间窗特征，晚于要求的最晚到达时间需要向司机支付加班费；

e)每辆电动汽车有一定的载重量，电动汽车所承载的货物量应在限制载重量之内；

f)电动汽车的电池SOC均在10%～90%之间，充入的电能最大为电池容量的80%[12]。

2.3 模型建立

根据上述定义，建立考虑充电时间的带时间窗的电动汽车路径规划问题的数学模型为

(3)

(4)

目标函数表示为最小化总成本，目标函数中第1项为电动汽车行驶的电能消耗，与行驶距离有关；第2项为违反客户时间窗的惩罚成本；第3项为违反行驶终点时间窗的惩罚成本；第4项为电动汽车自身的固定成本；第5项为司机的酬薪成本。

约束条件如下：

a)每个客户点只能被访问1次：

(5)

b)充电站最多被访问1次：

(6)

c)电动汽车均由行驶终点离开并最终返回出发点：

(7)

d)分别跟踪离开客户点和充电站后下个节点的到达时间：

(8)

式中：ti,0为客户点i的服务开始时间；tij为节点i到节点j的行驶时间；ti,s为客户点i的服务时间；Tmax为电动汽车行程时间最大限制；S′为充电站及其副本的集合；V0为客户点和出发点集合。

tij- (Tmax+tc,max+tw,max+tmax)×

(9)

式中：ril,d为电动汽车离开充电站i时，充电时间曲线分段点l的系数；ril,a为电动汽车到达充电站i时，充电时间曲线分段点l的系数；tl为充电时间函数上分段点l对应的时间；ti,w为电动汽车在充电站i的等待时间；tc,max为将电动汽车电池从10%充电至90%所用的时间；tmax为所有路线中用时最长的时间；tw,max为最长等待时间。

e)分别跟踪上一节点为客户点和充电站的路线总用时：

(10)

式中：ti,N+1为节点i到行驶终点行驶时间；xi,N+1,m为决策变量，具体描述为

(11)

ti,N+1- (Tmax+tc,max+tw,max+tmax)×

(12)

f)离开节点i和到达节点j需要在同一时间段内：

(13)

(14)

g)保证返回行驶终点的时间在同一时间段内：

tmxi,N+1,m≤fi≤tm+1+Tmax(1-

xi,N+1,m),i∈V′,m∈M.

(15)

h)客户点服务时间不能早于客户要求最早服务时间：

ti,e≤ti,0,i∈V.

(16)

式中ti,e为客户点i要求的最早服务时间。

i)晚于客户要求最晚服务到达时间到达客户点时，迟到时间为正值：

ti,v≥(ti,0-ti,z),i∈V.

(17)

式中ti,z为客户点i要求的最晚服务时间。

j)电动汽车总行程时间需要小于最大时间限制：

ti,t≤Tmax,i∈V′.

(18)

k)晚于行驶终点要求最晚返回时间时，迟到时间为正值：

tN+1,i≥(ti,t-tgb),i∈V′.

(19)

式中tgb为行驶终点时间窗关闭时间。

l)将等待时间与决策变量xij,m建立联系：

ti,w(tj,0)≥bj,m+kj,m(tj,0-tm)-tw,max(1-

xij,m),i∈V0,j∈S′,m∈M.

(20)

式中：bj,m为时间段m下充电站j的等待时间函数的截距；kj,m为时间段m下充电站j的等待时间函数的斜率。

m)判断到达和离开充电站i时电动汽车的电池SOC：

(21)

式中ai,a为到达充电站i时的电池SOC。

(22)

式中ai,d为离开充电站i时的电池SOC。

n)分别跟踪离开充电站和离开客户或行驶终点的电动汽车电池SOC：

(23)

式中：h为耗电系数；Vcom为i，j组合的集合。

(24)

o)所有电动汽车电池SOC均在10%到90%之间：

(25)

(26)

p)跟踪电动汽车的载重量并保证载重量在限制内：

0≤u0≤uev.

(27)

式中：u0为电动汽车始发时的载重量；uev为电动汽车的最大载重量。

(28)

式中：ui为到达节点i时电动汽车剩余的载重量；uj为到达节点j时电动汽车剩余的载重量。

q)建立变量zil和yil的关系及电动汽车到达充电站i时的充电时间曲线分段点l的系数：

(29)

式中zil为决策变量，具体描述为

(30)

(31)

式中yil为决策变量，具体描述为

(32)

r)确保近似充电函数系数取值正确：

ri0,a≤zi1,i∈S′.

(33)

ril,a≤zil+zi,l+1,i∈S′，l∈B{0，b}.

(34)

rib,a≤zib,i∈S′.

(35)

ri0,d≤yil,i∈S′.

(36)

ril,d≤yil+yi,l+1,i∈S′，l∈B{0，b}.

(37)

rib,d≤yib,i∈S′.

(38)

s)确保电动汽车不会连续访问充电站点：

(39)

t)规定决策变量的取值范围：

(40)

zij,m≥0,i∈S′,j∈VN+1,m∈M.

(41)

yib,zib∈{0,1},i∈S′，b∈B.

(42)

ai,a,ai,d,ti,w≥0,i∈S′.

(43)

ti,v≥0,i∈V.

(44)

ti,0,ti,t,tN+1,i≥0,i∈V′.

(45)

ril,a,ril,d≥0,i∈S′,l∈B.

(46)

3 自适应大规模邻域搜索算法

ALNS是邻域搜索算法的衍生算法，可以破坏和修复当前解并产生新的解[13]，将新解与当前解比较以决定是否将新解作为局部最优解；同时算法本身可以根据邻域解的质量，自主选择合适的破坏和修复算法来进行邻域搜索，最终得到整体最优解。ALNS算法的基本步骤为：构建初始解和自适应大规模邻域搜索。

3.1 构建初始解

初始解可以由构建1个可行的路线来产生。构建可行路线由距出发点最近的客户开始，接着计算所有未分配的客户点，并按照时间窗的要求插入路线中可行点中的成本，然后执行成本最低的插入操作[14]。如果由于电动汽车电量不足，无法将客户点插入路径中，就将客户和充电站一起插入到路径中；如果由于不满足时间窗或电动汽车载重量满载的要求，而导致无法将客户点插入到路线中，则放弃此路线并重复构建过程，直到所有客户点都被插入到路线当中。由此构建出1条包含所有客户点并且满足时间窗的路线，以此作为初始解。

3.2 自适应大规模邻域搜索

构建出初始解后，ALNS算法开始迭代改进解，直到满足停止条件。在迭代过程中，首先执行破坏操作，将当前解中的部分客户点和充电站节点移除。客户点的移除数量γ是均匀分布于客户点移除最小数量nc,min和最大数量nc,max之间的随机数。客户点的移除方式有4种：

a)随机移除γ个客户点产生新的路线方案；

b)计算路线中所有中间有1个客户点的节点对之间的路线距离，选择距离最长的γ个节点对之间的客户点进行移除操作；

c)计算路线中所有中间有1个客户点的节点对之间的路线行驶时长，选择用时最长的γ个节点对之间的客户点进行移除操作[15]；

d)选择所有与充电站点相邻的客户点，计算在这些客户点于其相邻的充电站点之间行驶消耗的成本，选择成本最大的γ个客户点移除[16]。

在移除了部分客户点后，可能会出现不再需要部分充电站的情况；计算移除这些不再必需的充电站点目标函数的减少量，选择目标函数减小量最大的充电站点移除；重复这一过程直到路线中不再存在非必需的充电站点[17]。至此，算法迭代一次的破坏操作完成。

破坏操作完成后执行修复操作，将移除掉的节点插入到路线中来尝试得到更好的路线方案[18]。客户点的修复操作有2种方式：

a)计算在所有可行节点对之间插入客户点而造成的成本增加量，选择成本增加量最小的节点对插入客户点；

b)计算插入客户点后路线总用时间，选择总时长最短的位置插入客户点[19]。

完成客户点插入后，再进行充电站点的修复操作，通过计算找出电动汽车以负值电量到达的客户点，并在此客户点与上一个客户点之间插入1个对路线距离增加量最小的充电站点[20]。待所有被破坏操作移除的节点被修复操作插入回路线后，算法完成1次迭代，形成1个新的解。通过比较迭代得到的新解与当前解的目标函数值来决定是否将新解作为新的局部最优解，以及对迭代过程中采用的破坏操作和修复操作进行权重更新。

破坏和修复操作有很多种，每个操作o都有对应的权重ωo和分值πo，较高的分值表示操作的高性能，应该具有更高的选择几率。最初所有算法具有相同的权重和同为0的分值，在迭代过程中，如果产生了新的局部最优解，本次迭代中采用的破坏和修复操作的分值会增加σ1；如果迭代产生的新解优于当前解但不是最优解，本次迭代采用的破坏和修复操作的分值会增加σ2；如果迭代产生的新解比当前解要差，则本次迭代采用的破坏和修复操作的分值会增加σ3[21]。每次迭代开始时，每个破坏和修复操作的权重更新为ωo=ωo(1-p)+pπo/θ；其中p为区间(0,1)之间的随机数，θ为自上次分值更新以来操作被使用的次数[22]。操作的选择几率为

ωo/∑k∈Oωk,

(47)

式中O为操作的集合。

4 算例测试与分析

本文采用EVRPTW问题经典Benchmark例子[23]，以物流电动汽车为例进行实验。对上文提出的模型及算法采用Java语言编程，所有实验运行在英特尔Xeon E5 2.10 GHz处理器16 GB内存的虚拟机上。算例中的客户点有3种分布情况：集中分布(C)、随机分布(R)和集中随机分布(RC)。

4.1 实验设计

本文采用与EVRPTW问题标准集的固定充电速率不同的非线性充电函数，并用三段线性函数近似表示，这意味着需要3种不同的充电速率。

实验将1 d分为5个时间段，并遵照“先进先出”的原则加入过渡区。假设从交通不拥挤时段过渡到拥挤时段需30 min，由于到达率的增加是外部因素，可以确定到达率增加可以在30 min内完成[24]。从交通拥挤时段过渡到交通不拥挤时段，由于充电站排队等待时间的存在，过渡过程可能会超过30 min。同时，电动汽车在早晨08：00离开配送中心，且必须在晚上20：00前回到配送中心，如果电动汽车在18：00后才回到配送中心，需要支付超时工作成本。等待时间曲线如图5所示，显示了1 d内不同时刻下的平均排队等待时间，其中横坐标表示时刻，纵坐标表示表示等待时间，单位为min。用于对比，实验中还设计了另一种时不变等待时间的场景，这种场景下，全天各时段的等待时间均相同。

图5 时变等待时间曲线Fig.5 Time-dependent waiting time curves

模型中的参数设定为：ce=0.4，cp=1，cf=1 200，cd=1，co=11/6。客户点移除数量的参数设定为：nc,min=min{0.1|N|,30}，nc,max=min{0.4|N|,60}，其中N为算例中客户点的数量。

4.2 结果分析

对问题集C、R、RC分别进行等待时间场景及不考虑等待时间场景实验，得出电动汽车规划路径和成本等数据。表1为不同等待时间场景下对目标函数成本值的影响，其中表格中的数值为当前场景下的目标函数成本与不考虑等待时间时的目标函数成本之比。

由表1可以看出：等待时间会在一定程度上造成成本增加，且时变等待时间造成的成本增加量比时不变等待时间造成的成本增加量要多。此外，在R和RC场景下，等待时间对成本的影响要比在C场景下的影响要大，主要原因是在客户随机分布的情况下由于路径总路程更长而导致更多次的充电，图6反映了这一情况。

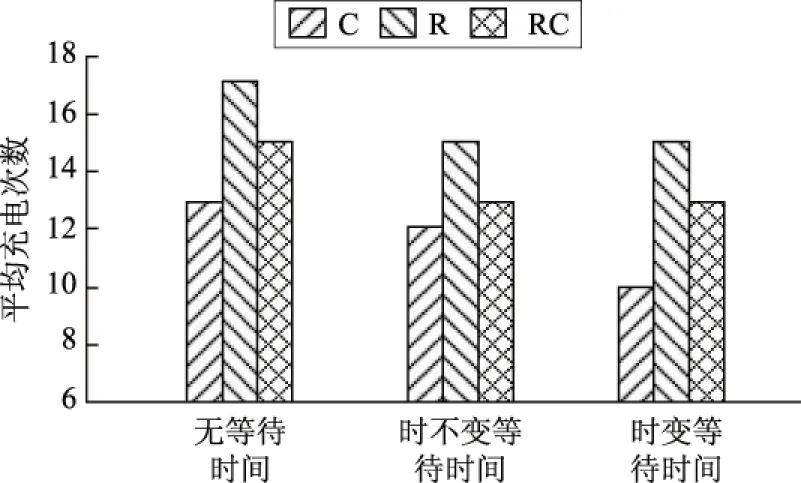
图6 不同场景下的平均充电次数Fig.6 Average charging times in different scenarios

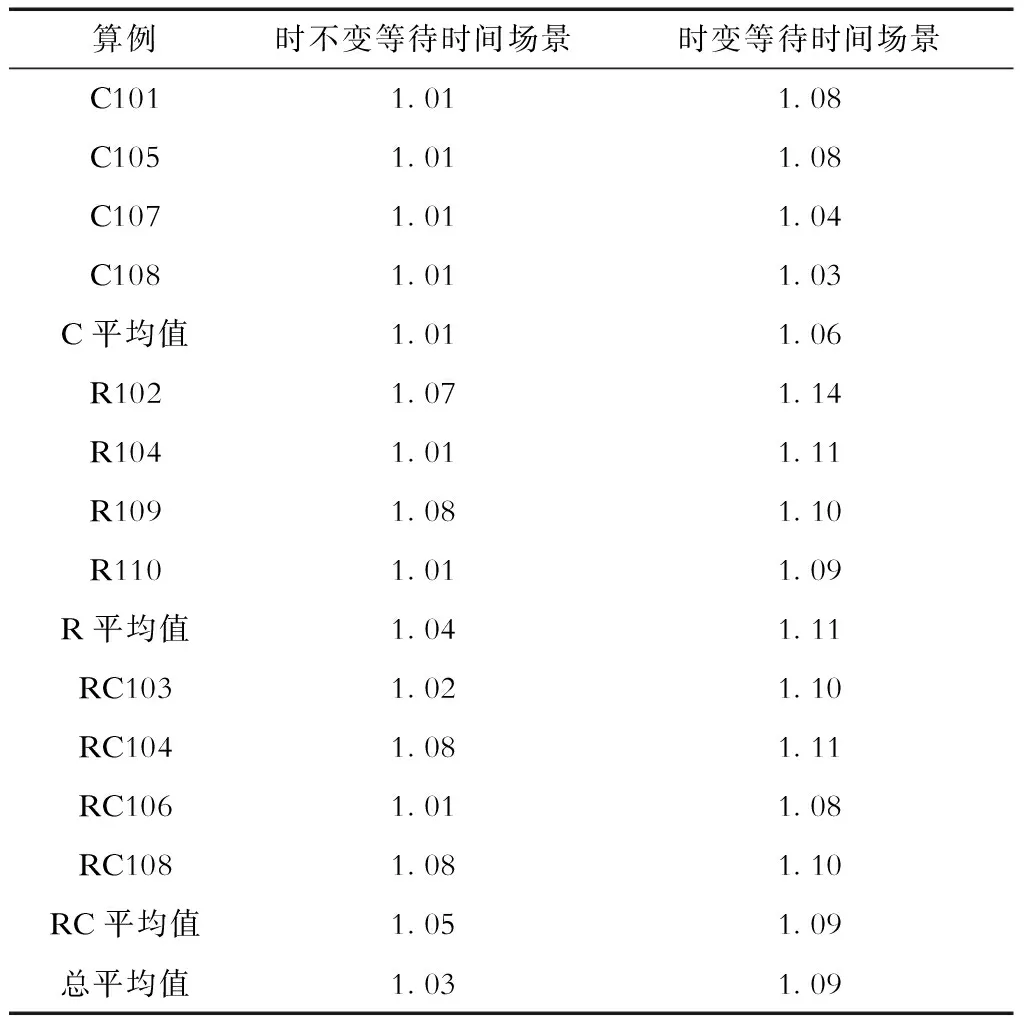
表1 不同场景下成本情况Tab.1 Cost situation in different scenarios

图 7所示为不同场景下各种成本与不考虑等待时间场景下各种成本比值的情况。

由图7(a)—(c)可以看出：等待时间对总成本、电动汽车固定成本和司机薪酬成本有近似的影响。图7(d)—(e)可以看出：超时工作的加班费成本和客户点迟到的惩罚成本的增加量在客户点集中分布的情况下比较多，这主要是因为在客户点集中分布的情况下电动汽车数量没有大规模增加而车辆会行驶更长的距离，这就导致会出现更多的客户点迟到的情况。图7(f)表明：电能成本相比与其他类型的成本较稳定，波动较小。同时，在客户点集中分布的情况下的电能成本水平非常小。规划通过增加电动汽车数量来避免频繁充电减少等待时间，这就使得解路线更加紧凑，一辆车访问不同区域的客户点的次数降低，因此减少了路线总距离，降低了电能成本。

图7 不同场景的各种成本比较Fig.7 Comparison of various costs in different scenarios

为了探究充电排队等待对路径问题决策及成本的影响，图8所示为各场景下算例的时间段分析。

图8(a)表明车辆在早上和晚上的充电量较少，结果符合车辆早上充满电开始配送而晚上配送服务量较少的现实情况。图8(b)同样表明了这一行为。为了避免较长的排队等待时间，以及减少因迟到而导致的成本，算法更倾向于为车队增加更多的车辆，这就使得完成配送任务所需要的充电次数和充电量都相对减少。图8(c)表明充电排队情况越严重，因迟到而导致的成本越高；且由于在早晨充电行为较少，在这一时间段内几乎没有出现迟到情况，但是到了中午和下午，迟到情况会明显增多。图8(d)展示了每种场景下的总能耗，可以看出各场景的总能耗基本一致，这表明路线行驶的总距离不受等待时间的影响，其影响表现在路径方案在车辆数量和充电时间上有所不同。

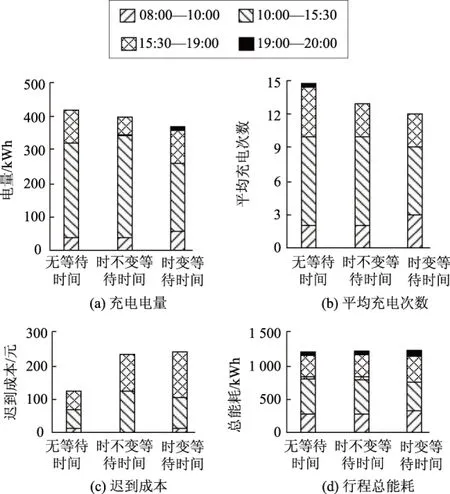
图8 充电决策和成本的时间分析Fig.8 Temporal analysis of recharging decisions and costs

5 结束语

本文介绍了考虑等待时间的带时间窗的电动汽车路径规划问题，并针对该问题建立了数学模型。采用ALNS算法对模型进行求解，从电动汽车行驶终点时间窗角度分析了充电站排队等待时间对路径成本的影响。现实的路径规划问题中，充电站一定会有排队的情况出现，本文提出的基于M/G/1排队系统的等待时间建模具有一定的实用性，也为路径规划问题提出了一种有效的解决方法；但也存在一定的不足，即未考虑电动汽车行驶过程中的不确定性情况，如路况、充电站配置情况、电动汽车电池的充放电特性等。针对这些问题，可结合问题情况提出更实用的解决方法。