换流变压器空载合闸励磁涌流有限元磁场仿真及受力分析

王仁，李正绪，杨家辉，薛海亮，李林达，吴佳麒

(1.广州西门子变压器有限公司，广东 广州 510530；2. 南方电网科学研究院有限责任公司，广东 广州 510663；3. 济南西门子变压器有限公司，山东 济南 250022)

目前，我国建设并投入使用世界最高电压±1 100 kV直流输电线路，换流变压器是其关键设备之一。国家电网有限公司、中国南方电网有限责任公司越来越重视关键设备在现场的运行情况，而空载合闸暂态过程正是每台变压器顺利投入运行的前提条件。换流变压器空载合闸励磁涌流现象除了对现场控制保护设定参数提出要求之外，换流变压器制造厂商也需要考虑在励磁涌流条件下的绕组内部受力情况。绕组内部受力取决于电流大小与磁场分布情况，但目前关于励磁涌流条件下变压器内部磁场分布情况及受力分析没有明确的参考方法，因此开展变压器在励磁涌流条件下的磁场分布及绕组内部受力的仿真研究十分有必要。

目前诸多文章中采用MATLAB、PACAD软件的内嵌电路模块进行的电流仿真[1-4]，其中少部分文章提到过励磁涌流条件下的内部磁场分布情况[5-7]，但并未对励磁涌流条件下变压器内部的饱和程度进行过详细介绍。本文认为励磁涌流需采用有限元磁场方法进行仿真，并对其内部磁场分布进行分析判断，进一步得到受力情况下的边界条件设定依据，为此提出一种采用2D有限元轴旋转场域考虑换流变压器不同切面条件的绕组受力分析方法。励磁涌流条件下变压器内部绕组的受力分析流程如图1所示。

图1 变压器内部在涌流条件下的受力分析流程Fig.1 Internal force analysis flow chart of transformer under the condition of inrush current

1 励磁涌流场域仿真

1.1 空载励磁涌流产生机理

单相换流变压器空载条件合闸工况电路可以等效外施电压电源对电阻和电感回路进行充电的暂态过程，忽略系统阻抗该暂态过程的等效电路如图2所示[8-9]。图2中:U为电源源电压， S为电路开关，RT为线圈等效电阻，LT为线圈等效电感，Rm为铁心等效励磁电阻，Lm为铁心等效励磁电感。跟据电路基本原理，在正弦电压源励磁下可得到式(1), 对该微分方程进行求解，方程解可以得到周期磁通分量和非周期按照指数函数衰减磁通分量；另外如果考虑合闸前铁心中充有和非周期分量同相的剩磁φr，可以得到合闸后的磁通暂态式(2), 其中指数函数的时间常数与电路中的电阻值、电感值相关〔如式(3)〕。

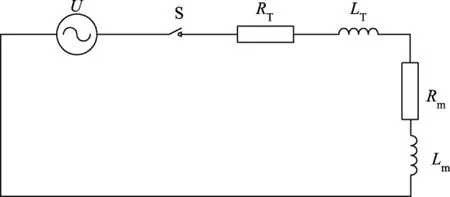
图2 变压器空载合闸等效电路Fig.2 Equivalent circuit of transformer no-load closing

(1)

φ(t)=φmsin(ωt+α-φ)-

(2)

(3)

式(1)—(3)中:N为合闸线圈匝数;φ为磁通量;φm为磁通量峰值；Um为电压源峰值;ω为电源角频率;α为电源初相角；φ为外施电压超前磁通量φ角度差值；τ为非周期磁通分量衰减时间常数；t为时间。

角度差值φ取决于电路的电抗与电阻分量〔见式(4)〕, 通常变压器的内部电感值远大于电阻数值，为了便于分析可以近似认为φ为90°，根据式(2)可得当电压初相角度为180°时，如果忽略非周期分量的微小衰减量，经过半个周期后，变压器的内部磁通可以达到最大值(2φm+φr)，工程经验φr近似为0.8φm，故该时刻变压器内部总磁通量可以高达2.8φm。

(4)

图3为当外施正弦电压初相角为180°空载合闸时一个周期内的磁通量变化曲线。其中：曲线1为外部施加激励电压波形；曲线2为铁心内磁通的周期分量；曲线3为铁心内磁通的衰减分量；曲线4为无剩磁条件下磁通波形，可由曲线2与曲线3叠加而得；曲线5为叠加剩磁条件下的磁通波形，它是由曲线4叠加0.8倍同方向剩磁得到的，且在合闸后半个周期10 ms时刻达到峰值。

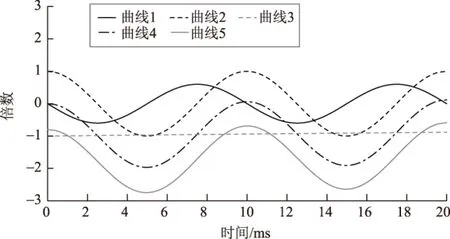
图3 空载合闸电压过零变压器内部磁通暂态变化曲线Fig.3 Transient changes of internal flux of transformer under the condition of no-load closing with voltage zero crossing

1.2 无剩磁条件下不同合闸角度涌流仿真值

换流变压器的励磁涌流仿真借助于Infolytica公司的Magnet软件3D暂态磁场求解器进行计算，模型建立考虑铁心、线圈、箱底磁分路、油箱磁屏蔽以及油箱关键部件，如图4所示；关键部件的材料名称及导磁特性见表1。为了加速励磁涌流暂态仿真的速度，换流变压器网格剖分四面体棱单元尺寸适当增加，但建议不大于400 mm，绕组漏磁变化敏感区域网格适当加密处理，器身网格剖分如图5所示。实际空载合闸的发送端换流变压器发生在网侧[10-13]，两心柱绕组绕向相同，为了等效两铁心柱产生反向磁通，将两心柱网侧绕组反接并联。暂态仿真电路连接如图6所示，其中:U1为电压源电压,R1为观测电阻阻值,S1为开关,COSA为柱1网侧绕组,COSB为柱2网侧绕组。

图6 空载合闸仿真电路Fig.6 Simulation circuit of no-load closing

表1 仿真材料属性Tab.1 Material Properties in the simulation

图5 器身网格剖分全局Fig.5 Overall situation of active part meshing

图4 变压器空载合闸仿真模型Fig.4 Simulation model of transformer no-load closing

仿真电压源是初相角为零的余弦电压波形，为了达到图3中显示的电压过零时刻合闸，开关S1设定在第5 ms时刻进行闭合，经过半个周期即第15 ms时刻励磁涌流达到峰值。励磁涌流仿真波形如图7所示，其中：第10 ms时铁心达到饱和，第15 ms时励磁涌流达到3 067 A的峰值，仿真结果符合预期。为了研究不同合闸角度对励磁涌流的影响[14]，对同一模型的合闸角，设定从0°到90°以18°作为步长进行仿真，图8显示了不同合闸角度励磁涌流的仿真结果，其中：在90°合闸时可以得到如图7所示的最大涌流峰值；在0°合闸的非周期磁通分量为0，变压器直接进入稳态过程，此时励磁电流仅为空载电流，仿真结果符合预期。

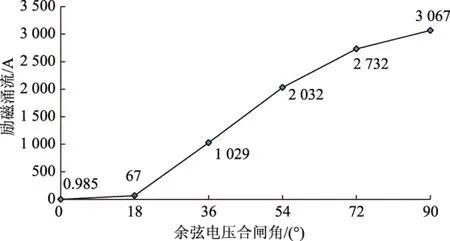
图8 不同空载合闸角度励磁涌流仿真结果Fig.8 Simulation results of excitation inrush current with different no-load closing angles

图7 空载合闸仿真结果Fig.7 Simulation result of no-load closing

1.3 最严苛合闸角叠加剩磁条件下的励磁涌流分析

根据上述分析可得：换流变压器空载合闸最大励磁涌流发生的条件是当外部电压过零合闸的工况，且经过半个周期之后励磁涌流达到峰值，但实际空载合闸前变压器内部可能存在剩磁，如果剩磁方向与非周期磁通方向一致，该剩磁会导致变压器内部最大磁通继续增加，即产生更大励磁涌流[15-16]。根据工程经验，合闸前剩磁为0.8倍稳态磁通量峰值，忽略剩磁分量在合闸后半个周期的微小衰减，合闸前的剩磁仿真可以通过恒定直流电源进行模拟。直流电源的数值设定需要先根据在正常励磁下空载电流有效值的0.8倍进行线性评估，然后再通过仿真验证进一步微调整，确保在合闸前铁心内部磁通达到0.8倍的最大磁通量。该案例的直流电源电流为0.41 A，空载合闸带直流充磁电源的电路如图9所示，其中：I1为电流源，R2为开断电阻。

图9 空载合闸带剩磁仿真电路Fig.9 Simulation circuit of no-load closing with residual magnetism

仿真电压源为初相角为0°的余弦电压波形，开关S1设定在第5 ms时刻进行闭合，经过半个周期即在第15 ms时刻励磁涌流达到峰值，铁心叠加0.8倍稳态磁通量剩磁的励磁涌流仿真峰值为6 504 A，剩磁是否存在对励磁涌流波形变化影响的比较仿真结果如图10所示。

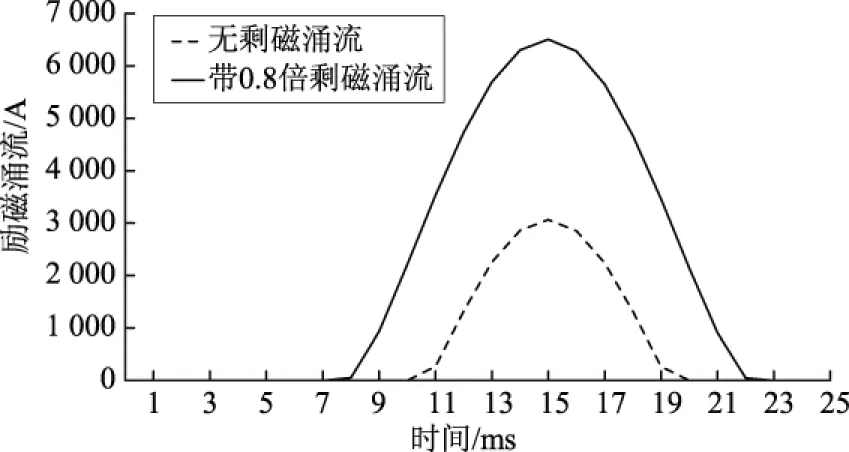
图10 剩磁对空载合闸励磁涌流影响的仿真波形对比Fig.10 Comparison of simulation waveforms of residual magnetism affecting no-load closing inrush current

带剩磁条件下的励磁涌流峰值Im也可以采用工程经验式进行计算[17]〔如式(5)〕。按照式(5)计算结果为6 850 A。仿真与式(5)计算结果相比相差5%，仿真结果符合预期。

(5)

式中φS为铁心饱和磁通。

2 励磁涌流下换流变压器内部受力分析

2.1 最大励磁涌流条件下的变压器内部饱和特性

根据上述励磁涌流的仿真结果，单相换流变压器励磁涌流峰值出现在电压过零合闸后的半个周期时刻。研究换流变压器内部的受力分析还需要考虑在励磁涌流峰值工况下的内部漏磁场分布情况[18]。最大励磁涌流条件下的铁心漏磁分布如图11所示，其主心柱内部最大磁通密度(简称“磁密”)出现在线圈中部区域，磁密峰值为3.12 T; 铁轭磁密峰值出现在两柱磁通交链的主铁轭内部中心区域，磁密峰值为2.438 T; 旁心柱最大磁密出现在中部区域，磁密峰值为2.26 T; 旁轭磁密峰值为2.20 T。可见在励磁涌流峰值时刻铁心各区域基本达到饱和，铁心主心柱区域饱和情况最为严重。

图11 最大励磁涌流时铁心磁密分布仿真Fig.11 Simulation of core flux density distribution with the maximum excitation inrush current

在最大励磁涌流条件下的磁屏蔽、磁分路漏磁分布如图12所示，其中靠近器身相中心的6组磁屏蔽全部达到饱和，磁屏蔽内部的最大磁密峰值为2.28 T ,由于端部漏磁弯曲的原因，正对线圈磁屏蔽的端部未达到饱和值;油箱底部磁分路漏磁峰值出现在两心柱绕组漏磁交链的相间区域，磁密达到2.30 T。在最大涌流条件下的油箱分路磁密分布如图13所示，油箱箱壁、油箱底部的器身中心区域达到高度饱和状态，这主要是因为两心柱线圈的漏磁在油箱壁相间、油箱底部区域进行交链，油箱磁密峰值达到2.37 T。

图12 最大励磁涌流时磁屏蔽及磁分路磁密分布仿真Fig.12 Simulation of magnetic shielding and flux density distribution of magnetic shunts with the maximum excitation inrush current

图13 最大励磁涌流时油箱分路磁密分布仿真Fig.13 Simulation of flux density distribution of the tank with the maximum excitation inrush current

为了确定饱和状态下的磁力线矢量分布情况，对仿真模型分别建立2个切面，如图14所示。切面1经过左侧线圈轴中心且垂直于油箱壁，切面2经过铁心中心内窗口。切面1的磁力线分布如图15所示，由于铁心内部发生高度饱和，磁力线方向沿铁心心柱方向，在线圈上下端部区域发生弯曲，并在上下铁轭高度一半方向弯曲严重， 磁力线在油箱区域方向垂直于油箱箱壁。切面2的磁力线分布如图16所示，由于铁心内部发生高度饱和，磁力线沿铁心心柱方向在铁心窗口内的上、下区域近似垂直进入铁轭，且在旁柱区域近似垂直进入旁心柱，建议2D仿真漏磁边界如图16所注边框所示。

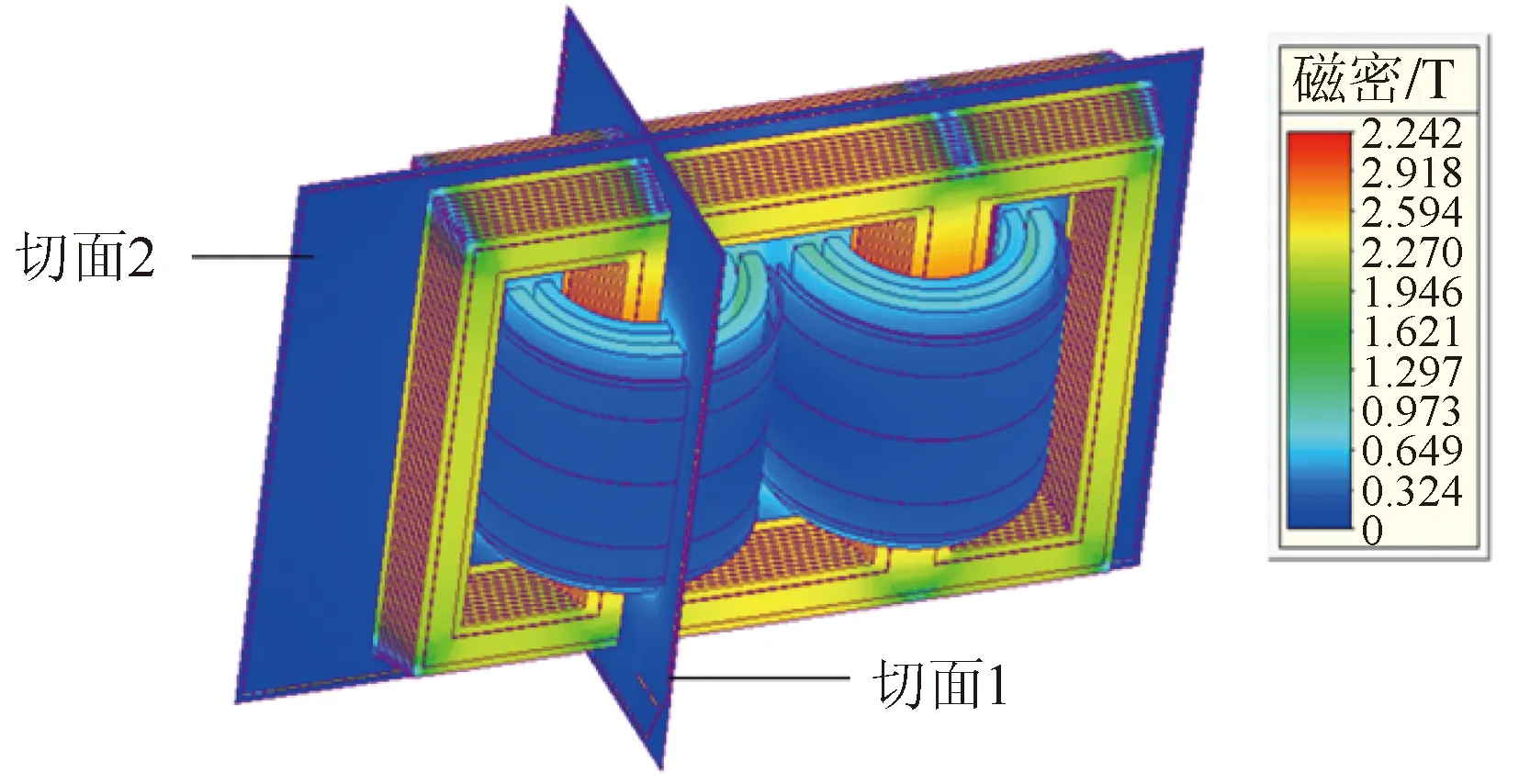
图14 器身模型不同切面Fig.14 Different sections of active part

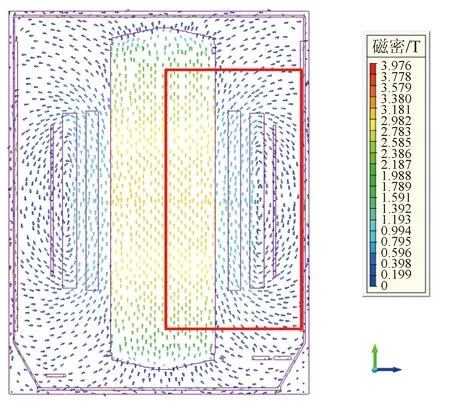
图15 切面1垂直箱壁切面磁力线分布Fig.15 Magnetic line distribution of vertical tank wall of section 1

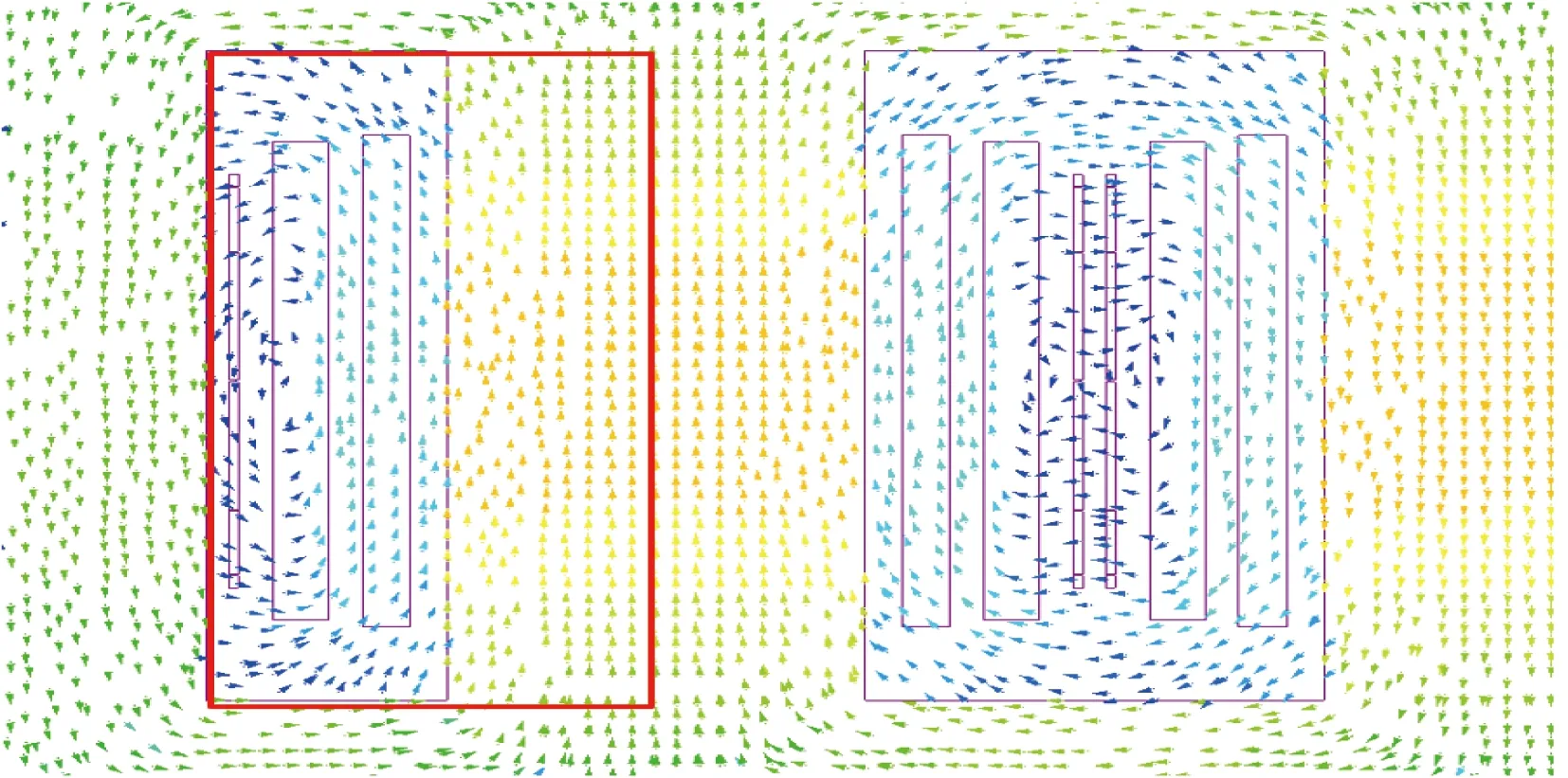
图16 切面2窗口内磁力线分布Fig.16 Magnetic line distribution in the window of section 1

2.2 涌流条件下的变压器内部受力分析

3D仿真模型的线圈简化为圆筒实体，无法反映绕组内部油道对漏磁的影响。建立实际匝模型进行仿真，计算时间过长无法满足工程设计需求，因此受力分析需通过2D有限元软件以达到提高计算效率的目的[19]。由上述最大励磁涌流条件下的饱和特性分析可知，不同切面条件下的磁力线分布存在差别，因此需要对2D轴旋转模型按照2个不同切面条件进行仿真，通过这2个极限状态下的受力分析来确定绕组在励磁涌流下的受力结果。

采用2D有限元轴旋转模型分别进行切面1和切面2的磁力线仿真。其中：切面1是以铁心中心、铁心上窗口加50%铁轭宽度、铁心下窗口减50%铁轭宽度、油箱内壁构成，切面1的磁力线分布仿真结果如图17所示；切面2是以铁心中心、铁心上窗口、铁心下窗口、旁柱表面构成，切面2的磁力线分布仿真结果如图18所示。

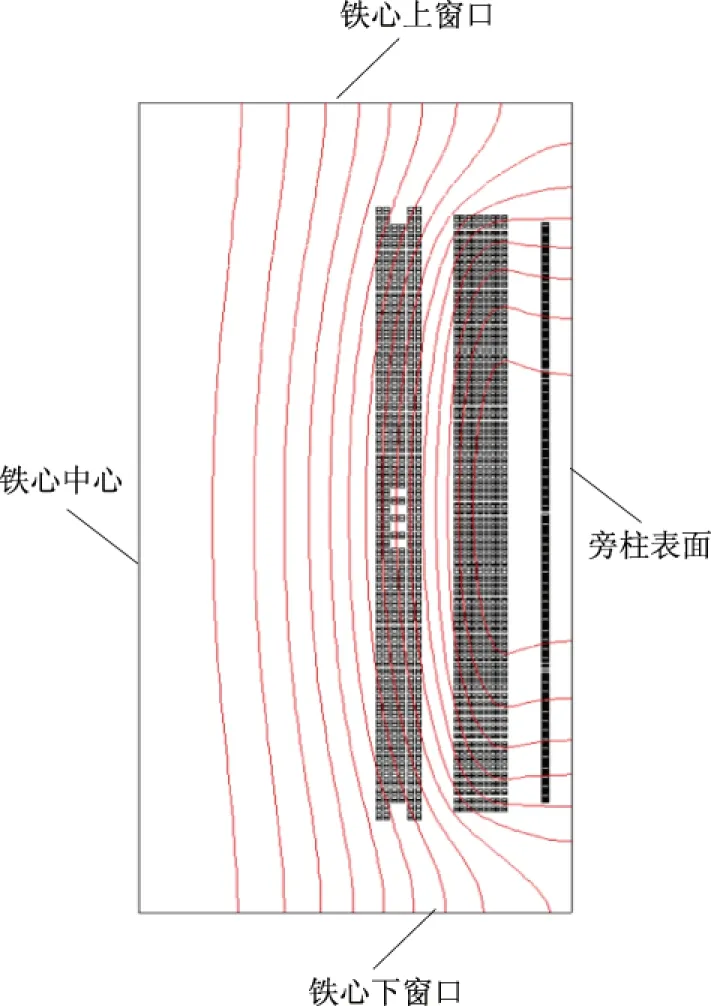
图18 2D轴旋转切面2磁力线分布Fig.18 Magnetic line distribution of 2D rotation section 2

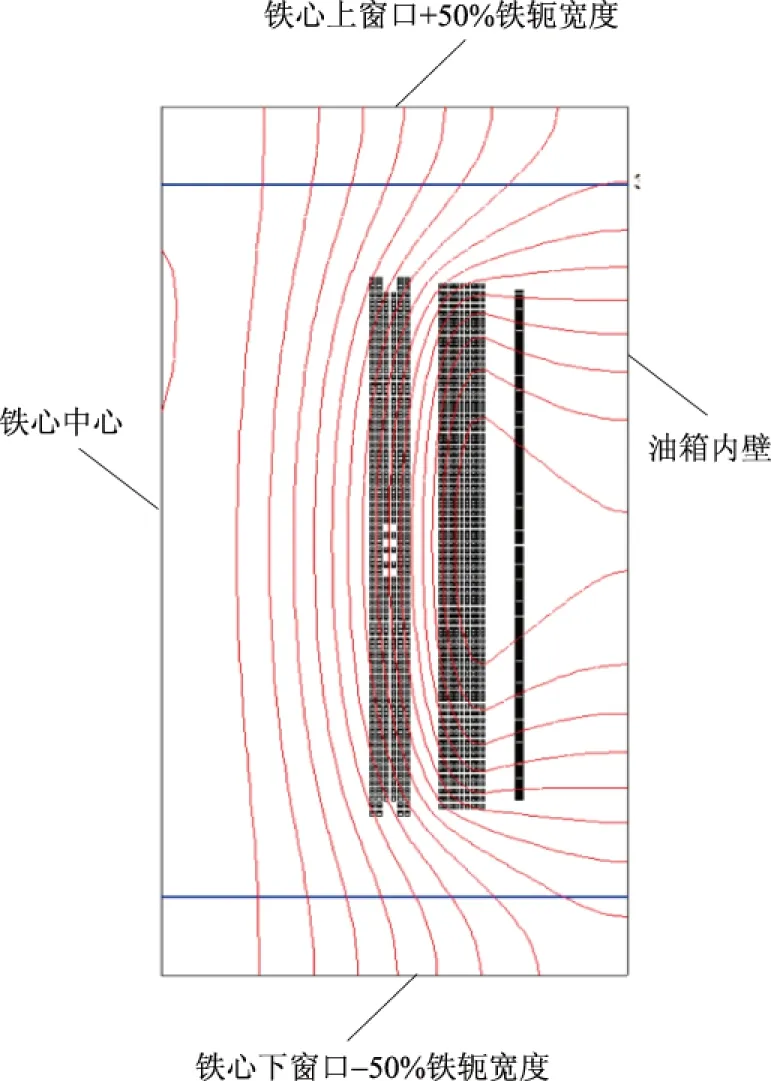
图17 2D轴旋转切面1磁力线分布Fig.17 Magnetic line distribution of 2D rotation section 1

根据不同切面漏磁力线弯曲方向及网侧绕组励磁涌流的电流方向，可以判断网侧绕组主要受到两端线饼向中间的轴向力以及线饼向外辐向力，体现在变压器设计中垫块之间的轴向弯曲应力以及导线自身环向张应力。网侧绕组在2个切面的条件下的轴向弯曲应力分布如图19所示。网侧绕组上、下端轴向力方向相反，因此线圈轴向应力上下2个部分的受力方向相反，正、负号分别代表向上和向下，由图19可知：油箱切面1最大轴向弯曲应力出现在线圈上部第1饼位置，数值为13.2 MPa，窗口数值为9.7 MPa；窗口切面2的最大环向张应力出现在中部第42饼位置，数值为11.2 MPa。通过不同切面的应力对比，轴向弯曲应力最大值出现在切面1油箱切面情况，辐向环向张应力最大值出现在切面2窗口切面情况，因此采用2种切面条件下进行2D有限元受力分析十分必要。

图19 不同切面轴向弯曲应力Fig.19 Axial bending force stresses of different sections

切面2的最大轴向弯曲应力出现在上部第1饼位置，数值为10.7 MPa。网侧绕组在2个切面的条件下的环向张应力分布如图20所示，其中：油箱切面1的最大环向张应力出现在中部第44饼位置，

图20 不同切面环向张应力Fig.20 Circumferential tensile force stresses of different sections

3 结论

本文以某实际工程换流变压器网侧绕组空载合闸为例，采用Magnet软件3D有限元电磁场域对不同合闸角度条件下的励磁涌流进行了暂态仿真，并对最严苛合闸角度叠加铁心剩磁工况下的励磁涌流进行仿真计算。在最苛刻励磁涌流条件下，对换流变内部磁性材料部件的饱和特性进行分析，根据其饱和条件下磁力线分布情况，提出一种采用2D有限元轴旋转场域考虑换流变压器不同切面条件的绕组受力分析方法，并得出以下结论：

a) 采用3D有限元电磁场仿真单相换流变压器励磁涌流，峰值发生在电压过零合闸后的半个周期时刻；如在电压峰值时刻合闸，变压器直接进入稳态过程。

b) 合闸前的剩磁仿真可以通过恒定直流电源进行模拟，在0.8倍最大磁通量剩磁下的励磁涌流仿真峰值为6 504 A；采用工程经验公式，励磁涌流峰值的计算结果为6 850 A。仿真与工程经验公式结果相比相差5%，故该仿真方法有效。

c) 在涌流峰值条件下，铁心各区域磁通基本达到饱和状态，铁心主心柱区域饱和最严重，磁密峰值为3.12 T， 其中：靠近器身相中心磁屏蔽全部达到饱和，磁屏蔽的最大磁密峰值为2.28 T；油箱底部磁分路漏磁峰值出现在2个心柱绕组漏磁交链的相间区域，磁密为2.30 T；漏磁在油箱箱壁、油箱底部的器身中心区域达到高度饱和状态，油箱的磁密峰值为2.37 T。

d) 在励磁涌流峰值条件下，轴向弯曲应力出现在绕组端部的切面1油箱切面，辐向环向张应力出现在绕组中部切面2窗口切面，因此建议采用2种不同切面条件对励磁涌流进行2D有限元受力分析。