基于三点估计法的含分布式电源配电网无功优化
2020-07-27李妍马平孙晓
李妍,马平,孙晓
(1.青岛大学 电气工程学院,山东 青岛 266071;2.国网山东省电力公司青岛供电公司市北供电中心,山东 青岛 266000)
分布式电源作为能源低碳发展和电力系统改革转型的载体,有利于发展微电网、保护环境、缩小供电距离、带动国民经济。新型可再生能源中风能、太阳能资源分布广泛,技术成熟,发展潜力巨大。以风、光发电为主的分布式电源出力具有随机性和间歇性特征并受并网设备输出特性限制,因此对分布式电源并网带来的有功和无功功率分布、电能质量、保护设备动作等方面的影响进行研究非常重要[1]。高比例渗透率(分布式电源并网容量与系统容量的比值,美国《渗透率研究报告》认为分布式电源渗透率达到10%~20%时通常会对电网产生显著影响)的分布式电源并网可能会导致系统产生双向潮流,影响电压质量、系统网损,甚至对配电网运行产生威胁。而电力系统无功优化在电力系统运行分析和电网规划中应用广泛,可在满足基本运行条件下提高电力系统的电能质量,降低电力系统有功损耗,减少电压偏差[2]。目前电力系统提高电能质量的措施主要有无功补偿、带负荷可调变压器投切、综合调压等[3],分布式电源的配电网无功优化研究也逐渐发展为联合多目标优化,以计算全网网损、电压稳定性、经济成本等最为适用。求解算法以单目标和多目标粒子群优化(particle swarm optimization,PSO)算法、蝙蝠算法、遗传算法等智能算法综合应用为主。滕德云[4]建立系统有功网损最低与电压偏量最小的多目标无功优化模型,并运用一种新的启发式鲸鱼优化算法进行无功优化调度。张艺镨[5]建立分层支路潮流的混合整数非凸无功优化模型,然后通过极限场景约束对随机变量进行处理,最终达到系统运行网损最小和最大化消纳清洁能源的目的。
进行目标函数的求解首先要满足一系列电网运行约束[6],运用概率潮流计算能比较全面地反映系统实际运行中的随机扰动和不确定性因素。其中与随机采样相结合的蒙特卡罗模拟法可以直接仿真求出待求变量的概率分布,但随着样本容量的增大计算时间也变长。方斯顿[7]提出的基于Nataf变换的扩展蒙特卡罗概率潮流计算方法,输出准确性高,可有效减少蒙特卡罗法计算耗时。近似法(利用输入随机变量的数字特征近似描述系统状态变量统计特性的方法)以半不变量法[8]为主,需计算出随机输入变量、节点状态变量和支路潮流功率变量的各阶半不变量之后,通过级数展开求得概率分布,但要求输入变量之间不具有相关性且公式推导极其繁琐。解析法以点估计算法为主,根据随机变量的概率分布计算出期望、方差、偏度后进行采样,可根据函数关系直接得到输出变量的各阶中心矩,具有可同时处理不同概率分布随机变量、计算精度高、计算耗时短的优点。
随着分布式电源在配电网中的占比不断提高,系统中不确定因素在随机并网负荷的基础上还增加了分布式电源出力等不确定因素,使得配电网无功优化更加复杂,因此研究不确定因素下的配电网无功优化具有实际意义。基于此,本文在考虑配电网经济性和稳定性的基础上,建立全网有功网损期望最小、电压偏差期望最小、电压稳定性指标最小的多目标无功优化模型,应用三点估计法确定初始输入变量,该方法比两点估计法计算精度更高,能更好地体现风、光出力和负荷波动性。最后,通过改进PSO算法求解目标模型参数值,结合IEEE 33节点系统对该方法的有效性进行验证。
1 模型的建立
1.1 风电随机模型
风电输出功率受设备安装地点和大气条件影响,设定风速分布服从威布尔两参数分布,累积分布函数
(1)
概率密度函数
(2)
式(1)、(2)中:v为实时风速;a、b分别为分布函数的尺度和形状参数,可由平均风速μv和标准差σv近似求得。
(3)
(4)
式中Г为伽马函数。
风电输出有功功率
(5)
式中:vi为投入风速;vr为额定风速;vo为切出风速;Pr为风电机组额定容量。
1.2 光伏、配电网负荷随机模型
a)光伏发电中光照强度服从Beta分布,概率密度函数
(6)
式中:S为实际光照强度;Smax为某时段的最大光强;α和β为Beta分布的2个参数[9]。光能利用输出功率Ps和光照强度S的关系可描述为Ps=SAη,其中η为光能利用率,A为光照电池板有效面积。
b)一般假设并网负荷服从正态分布随机模型,以恒功率因数方式运行,以期望、期望比例方差表示其概率密度函数为[10]:
(7)
QL=PLtanφ.
(8)
式中:PL、QL分别为负荷的有功和无功功率;φ为功率因数角;μL和σL分别为负荷有功功率的均值和标准差。
2 三点估计法
三点估计法能够根据已知随机变量的概率分布,在求出输入随机变量的均值、标准差、偏度和峰度后求出输出随机变量的各阶矩,从而得到输出随机变量的统计特征,计算简单且计算精度高,在点估计法中经常使用,在处理电力系统不确定问题时也得到广泛应用。

xi,k=μi+ξi,kσi,i=1,2,…,n,
k=1,2,3.
(9)
其中ξi,k为每个采样值的位置系数,取其中一个采样点为xi的均值,即ξi,3=0,每个采样点所占权重为pi,k,则有:
(10)
式中qi,j为规格化的前四阶中心距(j=3时,qi,3为偏度系数;j=4时,qi,4为峰度系数),
(11)
则ξi,k、pi,k的解析式可表示为:
(12)
(13)
三点估计法使用随机变量四阶矩,同时考虑了偏度系数和峰度系数,比两点估计法仅考虑偏度的计算精度更高,可将概率潮流计算转换为确定性最优潮流计算[13]。利用随机变量3n个采样值,根据最优潮流计算函数关系Y=f(Xi)对运行参数进行2n+1次估计,可以得到每个估计点处运行参数的估计值,最后根据权重系数计算运行参数各阶矩估计值
l=1,2,3,….
(14)
式中:当l=1时,E(Y)为Y的期望;当l=2时,可得Y的标准差
(15)
3 目标函数的建立
3.1 目标函数
本文建立有功网损期望最小、电压偏差期望最小、电压稳定性指标[14]最小的联合多目标优化函数。由于各个单目标函数量纲不同,采用变权公式形成单一目标函数。目标函数为
F=λ1E(Ploss)+λ2E(ΔU)+λ3Lmax.
(16)
其中:
(17)
(18)
(19)
Lmax=max{L1,L2,…,Le,…}<1.
(20)
式(16)—(20)中:Nk为系统所有支路集合;Gij为节点i、j间支路导纳;Ui、Uj为节点i、j电压;δij为节点i、j间电压相角差;UN为节点i电压额定值;Uimax、Uimin为节点电压运行上下限;Xij为节点i、j间的电抗;Rij为节点i、j间的电阻;λ1、λ2、λ3分别为网损、电压偏差、电压稳定性在系统中的重要程度比例系数,λ1+λ2+λ3=1;Le为系统支路薄弱程度,Lmax为各支路Le最大值,Lmax越小,电压稳定性越高。
3.2 约束条件
a)等式约束条件包括有功功率约束和无功功率约束。有功功率约束为
(21)
无功功率约束为
(22)
式(21)、(22)中:i=1,2,…,m,m为系统中节点总数;Bij为节点i、j间支路电纳;θij为节点电压相角差。
b)不等式约束条件包括安全约束和设备运行约束:
QG,min≤QG≤QG,max;
(23)
Ui,min≤Ui≤Ui,max;
(24)
KT,min≤KT≤KT,max;
(25)
QC,min≤QC≤QC,max;
(26)
0≤Z≤Zmax.
(27)
式中:QG,max、QG,min为发电机无功出力QG的上下限;QC,max、QC,min为静止无功补偿器(static var compensator,SVC)容量QC的上下限;KT,max、KT,min为有载调压变压器变比KT的上下限;Zmax为可投切并联电容器组数Z的上限。
4 改进PSO算法
PSO算法[15]源于对鸟类捕食行为的研究,从随机解出发迭代寻优,期间通过适应度函数判断解的品质,可同时处理离散变量和连续变量,相比遗传算法具有更好的全局收敛性和更高的计算速度[16]。假设在一个n维的搜索空间中,粒子构成的群X=[x1x2…xn]T,其中第i个粒子在t时刻的位置为xid,t=[xi1,txi2,t…xid,t],d为当前维数。根据跟踪当前最优粒子的原理,粒子xi在t+1时刻速度vid,t+1与位置xid,t+1更新公式为
(28)
式中:ω为惯性权重系数;r1、r2为在(0,1)区间内分布均匀的随机数;c1、c2为学习因子;pid,t为第i个粒子在t时刻个体最优值;pgd,t为t时刻全局最优值。
为了提高收敛精度,避免算法陷入局部最优,本文通过以下2个方面来进行改进。
a)惯性权重系数的取值关系到算法性能的优劣,本文选择指数递减惯性权重策略[17],即
(29)
式中:ωstart为惯性权重初值,ωstart=0.9;ωend为惯性权重末值,ωend=0.4;T为当前迭代次数,Tmax为最大计算次数。
b)学习因子是调节个体与全局最优位置在速度更新中所占的比例,为了提高种群全局搜索能力,学习因子c1、c2更新公式如下[17]:
(30)
式中:c1start、c2start分别为c1、c2初始值;c1end、c2end分别为c1、c2终止值。
改进算法后,运用MATLAB工具箱对IEEE 33节点系统进行优化求解与仿真,计算流程为:
①输入配电网33节点线路参数、PSO算法参数,初始种群采用随机的方法产生;
②应用三点估计法对全体粒子进行初始概率潮流计算,求取网损、电压偏差期望和电压稳定性指标,计算目标函数值;
③评估种群粒子的适应度,确定局部最优值和全局最优值;
④更新迭代次数、权重系数和加速因子,进而更新粒子速度、位置;
⑤进行概率潮流计算和目标函数求取,重新评估适应度并更新局部最优和全局最优解;
⑥重复步骤④和⑤,判断是否满足约束条件和迭代次数;
⑦在约束条件范围内,输出目标函数最小值。
5 算例分析
选用改进IEEE 33节点测试系统,对本文所提无功优化方法进行验证。系统基准电压为12.66 kV,基准功率为10 MVA,总负荷为(3 715+j2 300) kVA。根节点(节点1)的电压幅值设为1.05(标幺值,下同),其余节点电压幅值在0.95~1.05。考虑分布式电源接入电力系统对潮流分布、电能质量的影响[18-23],确定分布式电源接入点为22、18、25、33。系统线路结构如图1所示,其中DG1—DG4为分布式电源。

图1 含分布式电源的IEEE 33节点配电系统Fig.1 IEEE 33 node power distribution system with DG
节点1连接有载调压变压器,变比调节范围为±4×1.25%,选择4个节点6、7、12、24各安装10组并联电容器,每组容量为50 kvar。节点17、32安装SVC,调节范围[0 kvar,800 kvar],调节步长100 kvar。节点18、33处分别接入额定功率0.6 MW的风电系统,风速服从a=10.7、b=3.97的威布尔分布,切入风速、额定风速、切出风速分别为3 m/s、12 m/s、25 m/s。节点22、25分别接入额定功率0.4 MW的光伏发电,Beta分布参数为α=0.58、β=1.51,分布式电源最大渗透率20%。各节点负荷服从正态分布,方差比例为期望的10%,功率因数恒定。
改进PSO算法参数设置:种群数30;最大迭代次数50;c1初始值2.5,终止值0.5;c2初始值0.5,终止值2.5。
优化策略考虑目标函数不同比例系数:策略1,只考虑网损最小,不考虑电压,λ1=1,λ2=0,λ3=0;策略2,不考虑网损,只考虑电压,λ1=0,λ2=0.5,λ3=0.5;策略3,同时考虑网损和电压,λ1=0.5,λ2=0.25,λ3=0.25。
5.1 系统优化结果分析
系统采用3种策略优化前后节点电压对比如图2所示。

图2 采用3种策略优化前后节点电压对比Fig.2 Comparison of node voltages before and after adopting three strategies
由图2可知分布式电源和波动性负荷接入配电网后,系统电压波动幅度较大,某些节点电压出现不同电压越限行为。经过无功补偿优化计算后,系统电压和网损都能得到很大改善,各节点电压均提高至0.95以上。
无功优化配置方案见表1,优化前后网损期望、电压偏差期望见表2。
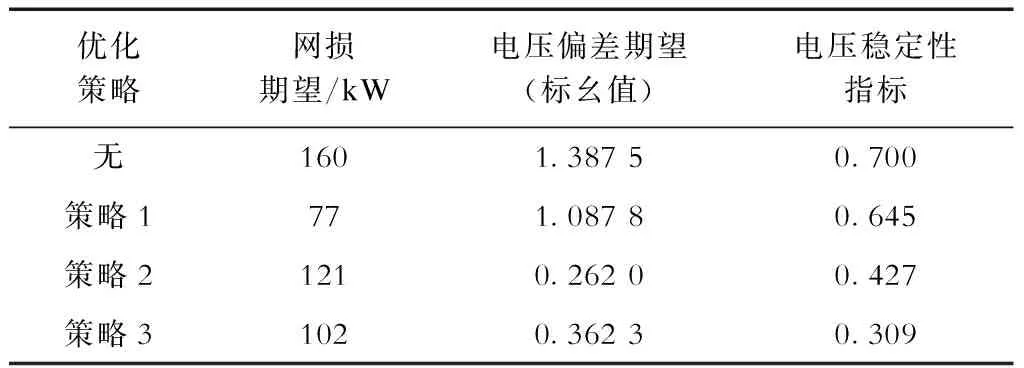
表2 无功优化前后的网损期望和电压偏差期望Tab.2 Expectation of of network loss and voltage deviation before and after reactive power optimization

表1 无功优化配置方案Tab.1 Reactive poweroptimization allocation schemes
策略1只考虑网损最小,不考虑电压;系统网损期望优化前为160 kW,优化后为77 kW,减少51.8%;电压偏差期望优化前为1.387 5,优化后为1.087 8,提高21.6%;电压稳定性指标提高7.9%。策略2不考虑网损,只考虑电压质量;网损期望优化后为121 kW,比优化前减少24.4%;电压偏差期望提高至0.262 0,提高81.1%;电压稳定性指标提高39%。策略3同时考虑网损和电压;网损期望优化后为102 kW,比优化前减少36.2%;电压偏差期望提高至0.362 3,提高73.8%;电压稳定性指标提高55.9%。经过综合分析可知,当考虑不同权重比的有功网损期望最小、电压偏差期望最小、电压稳定性指标最小的目标函数时,优化方法均适用。
5.2 算法有效性验证
5.2.1 不同概率潮流方法对比
在策略3条件下将三点估计法与蒙特卡罗方法、两点估计法进行比较,结果见表3。

表3 不同概率潮流方法比较Tab.3 Comparison of different probabilistic power flow methods
可以看出:三点估计法与蒙特卡罗法计算精度相差不大,而计算时间大大减少;三点估计法与两点估计法计算时间相似,而计算精度更高。因此,三点估计法可同时保证提高计算精度,减少计算耗时。
5.2.2 改进PSO算法与传统PSO算法对比
将传统PSO算法参数设置为:种群数30,最大迭代次数50,c1=c2=0.5。在策略3条件下将传统PSO算法、改进PSO算法各运行50次,得到的最优目标函数解如图3所示。
由图3可以看出:传统PSO算法在初始阶段具有较强的搜索能力,目标函数值下降较快,但最终优化结果不理想,迭代次数多,经36次迭代才基本达到最优解;改进PSO算法对全局搜索系数和速度因子进行改善后,仅迭代19次就达到最优解,比传统PSO算法优化结果更加理想,全局收敛性更强。

图3 PSO算法对比Fig.3 PSO algorithm comparison
6 结束语
本文针对分布式风、光电源出力和负荷的随机性,应用三点估计法处理概率潮流不确定因素,确定风、光出力和随机负荷的初始输入功率,得到系统输出变量的概率统计特征,提高了潮流计算的精度和速度。建立了考虑多重目标的无功优化模型,通过改进PSO算法优化全局收敛性,提高了计算速度。所提方法可有效减少风电、光伏和波动负荷并网电力系统的网损和电压偏差,提高系统稳定性。优化后各节点电压均提高至0.95以上,避免了电压越限行为,无功优化效果理想。
