无偏KL散度算法对时空异常区间检测的优化研究*
2020-07-27王梓宇
刘 云,王梓宇
(昆明理工大学信息工程与自动化学院,云南 昆明 650500)
1 引言
在许多数据挖掘任务[1 - 3]所用的原始数据中,或多或少都会存在一些数据异常的部分,这些异常数据可能是由噪声或观测误差等因素造成的无价值干扰,也可能蕴含着由罕见事件或复杂过程引起的有价值信息[4 - 6],检测并提取这些异常部分的方法在多个领域有着广阔的应用前景。然而大多数现有的逐点分析异常检测技术不能准确地反映数据的异常特征,部分异常区间检测技术,要么不适用于多变量时空数据,要么不能较好地检测大小变化的异常区间[7,8]。因此,有效检测多变量时空序列的异常区间是一个有价值的研究方向。
Keogh等[9]提出了一种使用符号聚合近似的启发式有序时间序列HOT SAX(Heuristically Ordered Time series using Symbolic Aggregate approXimation)算法。HOT SAX算法通过将长度为d的子序列表示为一个d维向量,计算该向量到其d维空间中最近邻的欧氏距离作为异常得分来提取时间序列中的异常子序列。该算法将检测序列的样本数(以下统称序列长度)事先指定为一个固定参数,由于时空序列中异常区间的长度通常不为定值,该固定参数的设定将影响算法的检测精度。Kim等[10]提出了一种鲁棒核密度估计RKDE(Robust Kernel Density Estimation)算法。将基于径向半正定核的核密度估计器KDE(Kernel Density Estimation)解释为相关再生核希尔伯特空间中的样本均值,用经典M估计来估计这些均值,可以得到加权核密度估计器(RKDE),通过收敛于RKDE的核化迭代加权最小二乘IRWLS(Iteratively Re-Weighted Least Square)算法计算权值,从而使RKDE能稳健地估计异常值。虽然KDE是一个灵活的模型,但其不考虑数据属性间的相关性且不能很好地扩展到长时间序列。
为了准确地找到多变量时空数据中的异常区间,本文提出了一种无偏KL散度UKLD(Unbiased KL Divergence)算法。定义时空数据中的异常区间后,算法首先为时间序列嵌入时间延迟,考虑样本之间的相关性;随后将检测区间和剩余区间估计为高斯分布,并通过累计和来加快参数估计过程;最后使用无偏KL散度计算分布之间的差异水平从而避免由区间长度产生的计算偏差。仿真分析结果表明,与HOT SAX算法和RKDE算法相比,UKLD算法在精度指标方面有优化提升。
2 模型
2.1 定义
[l,r)表示离散区间{t∈T|l≤t r≤n+1∧a≤r-l≤b} (1) 于是,时间序列X中所有符合给定约束大小A=(at,ax,ay,az),B=(bt,bx,by,bz)的子块集合定义为: (2) 其中,It、Ix、Iy和Iz分别表示时间点t和空间位置坐标x、y、z的符合约束大小(at,bt)和(ax,bx)、(ay,by)、(az,bz)的区间。 以下将JA,B省略索引简记为J。 给定任何区间I∈J,除了该特定范围外的时间序列的剩余部分定义为: (3) 以下简记为Ω。 定义的时间序列模型如图1所示。道格拉斯·霍金斯(Douglas Hawkins)把异常定义为“一个与其他观察结果偏离巨大的观察,以至于怀疑它由一个不同的机制产生”[11]。受该定义启发,相较于该时间序列的剩余部分Ω,时间序列X的一个子块I∈J由一个不同机制产生。于是,子块I称为时空时间序列X的一个异常区间,Ω为剩余区间。I与Ω的差异由差异水平度量D(pI,pΩ)定义。pI和pΩ分别为异常区间I和剩余区间Ω的概率分布。 Figure 1 An illustrative example of notations on time-series data图1 时间序列数据符号的说明性示例 散度KL(Kullback-Leibler)[12,13]是衡量2个概率分布之间差异水平的度量指标。2个分布的差异越大,KL散度值越大。区间I与Ω的分布pI、pΩ的KL散度定义如下: (4) 其中,pI(Xi)、pΩ(Xi)分别表示时间序列x中区间I与Ω的样本Xi中区间I与Ω的分布。 (5) 从而将先前时间步长中的上下文合并到时间序列的每个样本中。其中嵌入维度κ是堆叠的样本数量,时间延迟τ是被列为上下文的2个连续时间步长间的间隔。 为了灵活有效地估计嵌入时延的时间序列中异常区间I和剩余区间Ω的分布,在考虑数据属性间相关性的同时能扩展到长时间序列,假设区间I和Ω中的数据都服从多元正态高斯分布N(μI,SI)和N(μΩ,SΩ)[15]。 高斯分布模型需要对相应区间中所有样本求和来估计分布参数[15]。由于其中一些区间相互重叠,对多个区间执行求和是多余的,并且对大规模数据而言由于计算量过于巨大,这显然是不可行的。但是,使用累计和[16]后可以显著加快计算过程。 (6) 本文把无偏KL散度作为分布pI和pΩ的差异水平的度量,这是无偏KL散度算法UKLD的核心。首先分析KL散度DKL(pI,pΩ)的非无偏性,随后介绍无偏KL散度DU-KL(pI,pΩ)的理论推导。 (7) 由于时间序列的所有样本都服从正态分布,其均值也服从正态分布: (8) (9) 所以,平均向量μ的所有维度都是独立相同的正态分布变量,其差异也服从正态分布: (10) DKL(pI,pΩ)= (11) 其中,(μΩ-μI)i表示取向量μΩ-μI的第i维。 理论分析表明,KL散度不是无偏的,其系统地偏向于较小长度的区间。由于这种偏差与数据本身无关,与区间长度相关,较短区间将自动比较长区间获得更高的得分,所以异常值将被划分为多个连续的小区间,这明显降低了区间检测的质量。 当时间序列的长度n非常大时,卡方分布的尺度接近于: (12) (13) 渐进服从自由度为d+(d(d+1))/2的卡方分布。对于KL散度,样本集是异常区间I中的数据,用于检验该数据分布的参数由剩余区间Ω中的数据估计而来。于是检验统计量可用来度量检验区间I中的数据与基于时间序列剩余部分数据而建立的模型的拟合程度。 由式(11)定义的换算系数对KL散度归一化后,检验统计量λ与KL散度的关系为: λ=2m·DKL(pI,pΩ) (14) 因此,得到无偏KL散度为: (15) 该无偏散度由属性的数量d影响而不再是区间长度m,这能显著提高算法检测长时间序列中的长度变化异常区间的准确性。 得到所有区间的异常得分并按降序排序后,使用非极大值抑制方法以仅得到非重叠区间。对于样本超过10 000的长时间序列,使用近似非极大值抑制方法,通过维持一个固定大小的当前最高得分的非重叠区间列表,从而避免存储所有区间的得分。算法最后返回一个区间排名,输出前k个异常区间。 UKLD算法的流程如算法1中所示。首先为时间序列嵌入时间延迟,使用高斯分布估计检测区间I和剩余区间Ω的分布并通过累计和加快高斯分布的参数估计过程(步骤1~步骤3);随后使用无偏KL散度计算2个区间分布之间的差异水平,将该差异水平作为检测区间的异常得分(步骤4~步骤5)。最后使用非极大值抑制方法得到非重叠的异常区间(步骤6~步骤7)。 算法1UKLD算法 输出:非重叠异常区间。 步骤3pI(Xi)=N(μI,SI),pΩ(Xi)=N(μΩ,SΩ); 步骤4概率分布=∅; 步骤5对于∀i∈{1,2,…,n}: 步骤6用非极大值抑制方法确定非重叠异常区间I的集合; 步骤7返回异常区间I的集合。 与其他类似算法所采用的标准数据集一致,本文依据2017年1月1日至2017年9月30日间的丹麦欧登塞市[18]交通流计数来评估算法的性能。数据中的时间序列从高斯过程GP(h,K)中采样,h为零均值函数h(x) =0,K为平方指数协方差函数: K(xt,xt′)=(2πl2)-1/2· (16) GP的长度尺度为:l2=0.01,噪声参数为:σ2=0.001,δ(t,t′)为克罗内克δ函数。时间序列中异常区间的长度在时间序列长度的5%~20%变化,异常区间中的值是从高斯过程中采样的另一个函数值。测试数据集共有100个时间序列和190个异常。 仿真分析方法包括示例分析和量化分析,其中示例分析在截取一段代表性时间序列上比较3种算法提取的异常区间,通过对比该段时间序列上3种算法提取的同一异常区间的特点作判断。用方框表示异常区间,提取的异常区间越完整越精炼说明算法的精度越高。随后在数据集上做量化分析,在整个数据集上定量比较3种算法的精度,由于时空数据中异常区间检测是检测任务而非分类任务,把由交并比[19]量化定义的平均精度AP(Average Precision)作为精度指标。 从图2中可以看出,检测序列长度为125时,HOT SAX、RKDE和UKLD 3种算法都能找到该段时间序列中的3个异常区间。图2中,f(x)表示由高斯过程采样后时间序列的函数值,方框表示算法检测到的异常区间。图2a和图2c说明HOT SAX算法和UKLD算法的精度相差不大,UKLD算法略优于HOT SAX算法。图2b说明虽然RKDE算法找到的第1个和第3个异常区间与HOT SAX算法和UKLD算法的无明显差异,但第2个异常区间被RKDE算法分为2个连续区间,这会导致以后进行异常区间分析时结果不准确,所以RKDE算法的精度不如HOT SAX算法和UKLD算法的。 Figure 2 Anomalous intervals when length of the sequence is fixed图2 序列长度为定值时的异常区间 因此,当检测序列长度为125时,UKLD算法的精度最优,HOT SAX算法次之,RKDE算法较差。 从图3中可以看出,当检测序列长度设为25,75,125,150,200,250(归一化为0.1,0.3,0.5,0.6,0.8,1)时,随着检测序列长度的逐渐变大,3种算法的AP值逐渐升高,在归一化值为0.5(序列长度为125)附近到达最高,随后逐渐降低,算法的精度先升高后降低。对于检测序列的固定长度的不同取值(25~250),UKLD算法的AP值都要高于HOT SAX算法和RKDE算法的。在AP值最高点处,UKLD算法的精度在0.7附近,高于HOT SAX算法和RKDE算法的0.6附近的水平。即使在AP值最低(归一化值为1,序列长度为250)时,UKLD算法的精度仍在0.5附近,高于HOT SAX算法和RKDE算法的0.4附近的水平。 Figure 3 Accuracy comparison when length of the sequence is fixed图3 序列长度为定值时的量化精度 可见,对于检测序列的固定长度的不同取值,UKLD算法的精度高于HOT SAX算法和RKDE算法的。 从图4中可以看出,当HOT SAX算法设定检测序列长度为150,RKDE和UKLD算法设定序列长度取值为[25,175)时,3种算法都能找到该段时间序列中的3个异常区间。图4a和图4c说明UKLD算法较HOT SAX算法找到的异常区间的无用边界部分更少,算法精度更高。图4b说明虽然RKDE算法找到的第1个和第3个异常区间的精度介于UKLD算法与HOT SAX算法之间,但第2个异常区间被RKDE算法分为2个连续区间,这会使以后进行异常区间分析时结果不准确。 Figure 4 Anomalous intervals when length of the sequence is variable图4 序列长度为取值区间时的异常区间 可见,当检测序列长度为取值区间时,UKLD算法的精度较HOT SAX算法和RKDE算法有明显提升。 从图5中可以看出,当HOT SAX算法设定检测序列长度为50,100,125,150,200,250,RKDE算法和UKLD算法设定序列长度取值为[25,75),[25,125),[25,150),[25,175),[25,225)和[25,275)时(以上都归一化为0.2,0.4,0.5,0.6,0.8,1),随着检测序列长度取值区间逐渐变宽,UKLD算法和RKDE算法的AP值逐渐升高并趋于平稳,算法的精度逐渐变高并趋于稳定。由于HOT SAX算法只能把检测序列的长度设为定值,故算法的AP值折线图同图3无异。因此,对于检测序列长度为取值区间的情况,随着取值区间逐渐变宽,序列长度固定的HOT SAX算法的精度明显不如RKDE算法和UKLD算法的。 Figure 5 Accuracy comparison when length of the sequence is variable图5 序列长度为取值区间时的量化精度 对于检测序列长度的任意取值区间,UKLD算法的AP值都明显高于RKDE算法的。随着AP值趋于平稳后,UKLD算法的精度稳定于0.85附近,仍明显高于RKDE算法的0.7附近的水平。 可见,对于检测序列长度为取值区间的情况,UKLD算法和RKDE算法的精度指标较序列长度固定的HOT SAX算法有明显提升。对于检测序列长度的任意取值区间,UKLD算法的精度明显高于RKDE算法的。 为了从大量的多变量时空数据中发现数据异常的部分,本文提出了一种无偏KL散度算法(UKLD)。通过定义时空时间序列中的差异区间,在嵌入时间延迟后估计区间的分布,用累计和来加快参数估计过程,最后通过推导定义的无偏KL散度计算区间之间的差异水平来降低KL散度的计算偏差,将该差异水平作为检测区间的异常得分,从而得到时空数据中的异常区间。仿真结果表明,UKLD算法在精度指标上有明显优化。未来工作的方向主要是对时间间隔本身进行深入分析来降低算法的计算成本,同时深入探索对于高维数据的有效概率密度估计来进一步提升算法的准确性。

2.2 KL散度
3 无偏KL散度(UKLD)算法
3.1 预处理



3.2 无偏KL散度
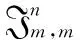



3.3 算法流程

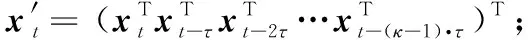

3.4 算法的复杂度分析
4 仿真分析
4.1 数据集
4.2 固定序列长度的精度分析


4.3 区间序列长度的精度分析


5 结束语
