基于单目视觉的车辆下边沿估计和逆透视变换的车距测量*

王永森，刘宏哲

(北京联合大学北京市信息服务工程重点实验室，北京 100101)

1 引言

随着经济的快速发展，我国的机动车产量和保有量已经连年高居世界第一，机动车虽然给人们的生活带来了方便，但也使交通事故频发，其中由于驾驶员操作不当而引发的道路交通事故占到了总事故的70%以上。自动驾驶汽车的发展能够有效地解决这一难题，保障交通系统的运行安全并且提高运输效率，对促进国民经济的发展具有重要的意义和经济价值。作为自动驾驶汽车重要组成部分，驾驶场景视觉感知与分析已经成为自动驾驶领域中的重点研究对象，其中前方车辆检测是场景感知工作中至关重要的一部分，并且准确测量当前车辆与前方车辆之间的距离可以对车辆进行准确定位，对自动驾驶场景分析与决策系统起着非常重要的作用，对安全行车意义重大[1- 6]。

目前，驾驶环境下前方车辆测距方法根据传感器不同分为基于雷达和基于视觉2类。基于毫米波雷达和激光雷达等主动式传感器的测距方法[7 - 9]虽然测距精度较高，但价格昂贵，同时易受外界环境干扰。基于视觉传感器的测距方法应用范围广泛，所获得的信息丰富，价格低廉，并且目前已经出现了很多优秀的目标检测算法[10 - 16]，为视觉测距提供了很好的目标定位基础。基于视觉的测距方法又分为基于单目视觉和基于多目视觉2类。基于多目视觉的测距方法[17 - 19]需要融合多个摄像头的信息，算法复杂，计算量大，相机标定困难，成本相对较高。基于单目视觉的测距方法实现原理简单，成本低廉，实时性更好。

近年来，国内外对单目视觉测距方法的研究取得了一些进展。文献[20]提出了一种面向未来智能交通的自适应前方车辆单目视觉测距方法，通过计算图像坐标系下车道标志线、交通标志、车辆尺度信息，依据相机成像数学模型计算前方目标车辆距离，但其需要特定场景环境，需要获取多个道路相关信息，不具普适性。文献[21]为了克服传统单目视觉测距中时变的摄像机外参数对测量结果的影响,利用道路车道标识线平行约束条件,提出了一种基于车道线消隐点的单目视觉自适应车辆测距方法，但其需要对道路车道线信息进行提取，测距精度受车道线提取准确度的影响，只适用于特定结构化道路。文献[22]提出了一种使用单目相机估算车辆在弯道时前方车辆距离的算法，通过分析车辆在弯道行驶时的特征对前方车辆进行检测，在此基础上实现车距测量，该方法受限于车辆在弯道行驶时的特征信息，只适用于特定场景。文献[23]利用光流法来计算前方车辆距离，从单目相机测得的光流和车辆控制端的信息来估计车辆的距离和速度，但该方法依赖控制信息，且受光变环境影响较大，不具有普适性。

文献[24-26]所研究的测距方法是基于相机成像横向模型算法来计算目标车辆的距离，该方法需要已知目标车辆的实际物理宽度，车辆宽度大约在1.4～2.6 m，根据相似三角形原理计算车辆距离，如果预估的车辆宽度和实际车辆宽度有较大差异则会产生很大的测距误差。文献[27]利用纵向测距模型来计算车辆距离，基本原理也是根据相机成像原理，但是与利用横向测距模型方法不同的是，他们的方法是用自身的相机高度来代替车辆的物理宽度参数，这样相当于已知一个较为准确的物理值，不需要估算车辆的宽度，提高了测距的精度。但是，该方法忽略了车辆下边沿问题，无法确定车辆与地面相接的准确位置信息，且受相机安装角度的精度影响，导致测距误差的产生。文献[28]提出了一种基于水平方向和垂直方向的相似三角形测距方法，减少了由于车辆自身在远距离上的俯仰角而导致的误差，但该方法没有考虑到车辆与地面相接的下边沿位置问题，造成测量误差。文献[29]提出了一种基于逆透视变换的测距方法，利用逆透视变换得到道路俯视图，根据线性关系进行距离计算，该方法虽然简单易行，但忽略了车辆测距的关键点选取问题，只能估计车身整体大致位置，无法精确定位，且对相邻车道内的车辆测距误差较大。

通过对上述研究成果进行分析，目前基于单目视觉的车辆测距方法忽略了车辆下边沿对测距产生的影响，导致测距关键点选取不够精准，造成测量误差的产生。为了提高驾驶环境中前方车辆单目视觉测距的精度和稳定性，本文提出了基于车辆下边沿估计和逆透视变换的车距测量方法，利用车辆关键点估计车辆三维信息，提取车辆与地面相接的下边沿位置坐标，计算测距关键点，通过基于点的逆透视变换测距模型，实现对车辆距离的高精度测量。

2 方法总体设计

如图1所示，为了实现车辆下边沿估计，本文方法借助基于深度学习的目标检测算法完成驾驶场景中车辆目标以及车辆关键组件的检测。车辆下边沿估计模型通过分析车辆视角，对车辆所处位姿进行分类，参照车辆组件位置，计算车辆关键点坐标，同时依据相机成像原理和几何先验模型进行车辆三维信息估计，得到车辆下边沿信息。逆透视变换模型根据相机成像原理对相机进行标定，得到相机内外参数，从车辆下边沿信息估计测距关键点坐标，根据逆透视过程，对测距关键点进行距离计算，完成车距测量。

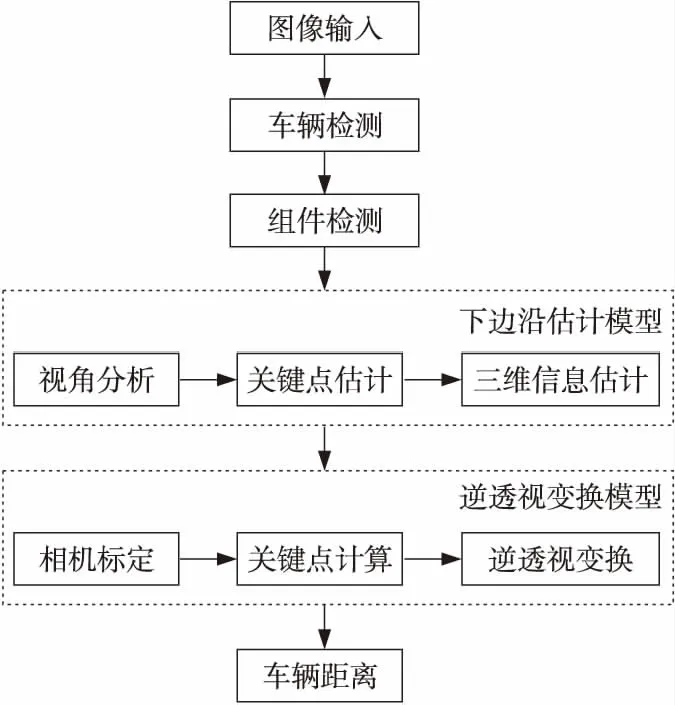
Figure 1 Overall design of the method图1 方法总体设计

3 车辆下边沿估计模型

车辆下边沿是车辆在道路上时车尾的垂直截面与地面相接的位置，如图2a所示，而常规的车辆检测结果如图2b所示。传统的测距模型建立在车辆矩形检测框的基础上，测距点的选择基于矩形框的下边，如图2c所示，通过对比，真实的车辆下边沿和检测得到的矩形框的下边存在差异，导致测距误差的产生。特别地，当车辆下边沿估计不准时，将对横向距离估计造成非常大的影响。为了从根本上提高测距精度，找到更加准确的车辆下边沿非常重要。本文建立车辆下边沿估计模型，对车辆下边沿进行估计。

Figure 2 Comparison of the lower edge of the vehicle and the detection rectangle图2 车辆下边沿与检测矩形框对比

3.1 车辆视角分析

车辆在行驶过程中，由于所在位置相对于当前车辆会时刻发生变化，相机所捕捉到的车辆在图像中会呈现不同的位姿角度，相当于观察车辆的视角不同，从而增加了车辆下边沿估计的难度。如图3所示，对车辆在行驶过程中的位置变化进行分析，观察车辆的视角变化的同时，车辆的下边沿相对于车辆矩形检测框的位置也发生变化。

Figure 3 Comparison of different vehicle perspectives图3 不同车辆视角对比

根据车辆位姿和观察视角的不同，将车辆关键点的选择分为2种情况：

(1)可以观察到车辆侧面的情况。

如图3所示，针对前6幅图像中可以确定车辆侧面的情况，即能看到车轮所在的侧面，如果不对车辆下边沿进行估计，而直接采取车辆矩形检测框进行距离测量，将会造成测距误差的产生，尤其对横向距离的估计影响较大。

如图4所示，为实现车辆下边沿的估计，本文分别选取车辆侧面的2个车轮和地面相接的地方作为2个关键点w0(w0(x)和w0(y)),w1(w1(x),w1(y))，除该2点之外，选取车辆车尾或者车头与相机中可以看到的侧面相交的棱，定义为直线L(x=p0)，其中p0为图像坐标横轴的坐标值，即需要的5个参数为N(w0(x),w0(y),w1(x),w1(y),p0)。

Figure 4 Vehicle side view图4 车辆侧方视角

(2)无法观察到车辆侧面的情况。

如图5所示，图像中的目标车辆相近于正前方车辆的观察视角，这种情况下车辆的下边沿和矩形检测框非常接近，使用矩形检测框作为车辆的下边沿进行测距所产生的误差相对较小。所以，对于该种情况的车辆不进行车辆下边沿估计，使用矩形检测框的下边作为车辆下边沿进行测距。

Figure 5 Perspective from the rear of the vehicle图5 车辆正后方视角

Figure 7 Key points estimation图7 关键点估计

在实际应用过程中，为了确定车辆所处的位姿以进行车辆关键点估计，定义变量λ,λ表示检测到的车尾矩形框中心点横坐标与车辆外接矩形框宽度的比值(车辆外接矩形框的左上角顶点位置为坐标原点)，根据λ的大小判定车辆所处位姿和观察视角，若λ∉[0.42,0.58]，属于车辆侧方视角；若λ∈[0.42,0.58]，属于车辆正后方视角。

3.2 车辆关键点估计

车辆关键点估计，首先利用目标检测算法[11,13]对图像中的车辆进行检测，得到车辆外接矩形框坐标位置B(x1,y1,x2,y2)，截取出车辆最小外接矩形框包围的像素信息。分析3.1节情况(1)中关键点位置信息，可通过对相应组件检测得到关键点位置坐标。如图6所示，利用2个侧方车轮和车辆尾部的位置信息，估计出车辆关键点。

Figure 6 Vehicle key components detection图6 车辆关键组件检测

使用SSD(Single Short multi box Detector)目标检测框架[13]对截取的矩形框包围的车辆图像进行检测，如图7所示，得到车轮的矩形框位置W0(x1,y1,x2,y2)、W1(x1,y1,x2,y2)和车尾的矩形框T0(x1,y1,x2,y2)。

关键点计算过程中，前侧车轮和后侧车轮组件矩形框分别使用wb0和wb1表示，它们可由式(1)和式(2)得到：

(1)

(2)

变量p0由式(3)得到：

(3)

2个关键点w0和w1的坐标由式(4)和式(5)得到，即G=(w0,w1,p0)。

(4)

(5)

3.3 车辆三维信息估计

如图8所示，车辆目标的三维信息在图像中使用顶点坐标表示为C={a,b,c,d,e,f,g,h}，其中，{a,b,c,d}表示目标车辆靠近相机侧垂直切面上从左上角按照顺时针方向的4个顶点在二维图像上的像素坐标点，{e,f,g,h}表示目标车辆远离相机侧垂直切面上从左上角按照顺时针方向的4个顶点在二维图像上的像素坐标点。

Figure 8 Vehicle 3D information图8 车辆三维信息

由G得到N=(w0(x),w0(y),w1(x),w1(y),p0)，依据几何模型计算车辆三维信息中的顶点坐标。计算过程如下：

如图9所示，由式(6)计算经过w0(w0(x),w0(y))和w1(w1(x),w1(y))2个关键点的直线方程F(x)：

(w0,w1)⟹F(x)

(6)

Figure 9 Vehicle 3D information estimation图9 车辆三维信息估计

由式(7)计算直线方程F(x)与直线L(x=p0)相交的点，记为构建3D立体框C={a,b,c,d,e,f,g,h}中的顶点d：

(7)

由式(8)可得直线方程F(x)与车辆矩形框左侧边K(x=k0)相交的点，记为C={a,b,c,d,e,f,g,h}中的顶点h：

(8)

然后取车辆矩形框右侧边下顶点为c点，取车辆矩形框左上角顶点为e点，由几何原理，依次平移线段eh到d点和c点，可得a点和b点，然后依次平移线段hd使d点分别和c点、b点重合，得到g点、f点，即可计算出车辆三维信息C={a,b,c,d,e,f,g,h}。

由车辆三维信息C={a,b,c,d,e,f,g,h}，一般情况下可直接由线段cd得到车辆下边沿，但关键点G会因组件检测的偏差导致误差增大，该情况下根据几何模型计算出的顶点坐标也将出现误差，随之估计得到的车辆三维结构将出现畸变，影响车辆下边沿估计的准确性。所以，为了降低误差，对C进行滤波校验。

在像素坐标系下，计算经过c和d2点直线的斜率kc d,kc d决定车辆下边沿在像素坐标系中的倾斜程度。根据驾驶场景中车辆的角度位姿先验，定义滤波函数Fsen(x)对其进行滤波，如式(9)所示：

(9)

通过式(9)完成对斜率kcd的修正，其中x表示斜率。利用相机投射投影成像存在消失点的原理[30-33]，对f、g和e进行修正，公式表示如式(10)～式(12)所示：

(10)

(11)

(12)

完成上述过程之后，校验几何模型是否满足式(13)所示的图像中像素坐标关系：

(13)

令三维信息估计结果标志变量为t，如果满足此条件，则t=1;不满足，则t=0。最后通过估计到的车辆三维信息，根据式(14)提取车辆下边沿R(x1,y1,x2,y2)：

(14)

4 逆透视变换模型

相机逆透视变换，目的是将图像像素坐标对应还原回物理世界坐标系中，得到图像的俯视图，如图10所示。相机成像的基本原理是将世界坐标系中的物理坐标点映射到像素坐标系中，过程如图11a所示，逆透视变换依据该原理，将像素坐标系中的像素坐标转换到世界坐标系中，为相机成像的逆过程,如图11b所示。

Figure 10 Inverse perspective mapping图10 逆透视变换

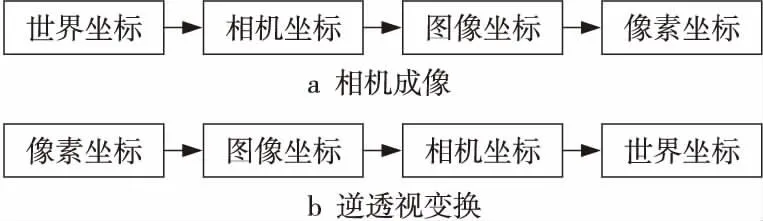
Figure 11 Coordinate transformation process图11 坐标变换过程

本文基于逆透视变换的测距模型的创新之处在于，利用前方车辆目标处在道路平面这一先验，结合标定原理，计算尺度缩放因子，然后进行基于点的逆透视变换实现测距，不同于利用全部像素逆透视变换之后的线性关系进行测距的方法。文献[29]采用的逆透视变换测距方法是将图像中道路信息还原成物理道路平面俯视图，利用该平面与真实道路平面具有的线性比例关系，确定车辆的距离。但是，该种方法忽略了车辆的视角姿态，在具有线性比例的关系图中难以找到车辆的下边沿位置坐标，只能近似估计车辆的整体车身距离，并且在对整体路面进行逆透视变换时需要对缺失的像素信息进行估计，从而增大了误差的产生。故本文方法先找到车辆下边沿，计算测距关键点，结合缩放因子，对该关键点进行逆透视变换，计算车辆距离，从而减小测距误差。

单目RGB相机在成像过程中，像素的深度距离信息会在相机坐标到图像坐标映射过程中丢失，如图12所示。在完成相机标定之后，得到相机外参旋转矩阵R3×3和平移矩阵T3×1。外参的作用是将世界坐标系和相机坐标系对齐，经过分析发现，外参包含一个隐藏的物理参数值，即世界坐标系原点和相机坐标系原点之间的位移，利用该物理参数值，以及目标车辆和当前车辆处于同一道路水平面先验，可求出道路平面像素点所对应的尺度缩放因子，从而实现基于点的逆透视测距。

Figure 12 Camera coordinate system and image coordinate system图12 相机坐标系和图像坐标系

逆透视测距详细过程如下所示：

令K3×3为相机内参矩阵(包含5个内参数)，表示为：

(15)

其中,f为相机焦距，dx和dy分别是相机横向和纵向单位像素的物理尺寸，(u0,v0)是图像坐标系原点O1在像素坐标系中的像素位置，r是内参矩阵因子。

设世界坐标系中的坐标点(Xw,Yw,Zw)，对应像素坐标系中的坐标点(u,v)，由式(16)所示的成像矩阵方程可得到式(17)：

(16)

其中,O为1×3的零矩阵。

(17)

(18)

通过4组对应点和单应性矩阵原理，可得相机参数P3×4。

由车辆下边沿信息R(x1,y1,x2,y2)和式(19)可得测距关键点像素坐标E(x,y):

(19)

令Zc=s,s即尺度缩放因子，由式(16)可得：

(20)

(21)

由车辆下边沿位置先验，得Zw=0，将Zw=0,(u,v)=E(x,y)代入式(21)，可得s=s0，又由式(21)可得：

(22)

Figure 13 KITTI dataset annotation information图13 KITTI数据集标注信息

5 实验

为了验证本文的测距方法，在具有雷达标注的距离信息的KITTI数据集[34]上进行实验。为了从多个角度对本文的测距方法进行验证，本文进行2组对比实验。第1组是将本文方法与未采用车辆下边沿估计直接进行逆透视变换的测距方法进行对比，目的是验证车辆下边沿对测距本身产生的影响；第2组是将本文方法与其他测距方法对比，目的是验证本文方法的测量精度。

本文从KITTI官方的训练数据集中去除用于训练检测网络的5 000幅图像，剩余的2 481幅图像用于实验验证。本文只对KITTI数据集中标签为“Car”类别的目标进行验证，并且对像素宽度小于100的车辆目标不进行下边沿估计操作，直接进行距离计算。KITTI数据集的标签格式如图13所示，每个TXT格式的标签文件代表对应文件名的图像中所有目标的信息，如图13中，每行数据代表一个实例目标，其中每行中的多个值使用空格分开。对本次实验中需要用到的标签数据进行如下说明：首先，每行中的第1个值为字符串类型，表示该目标的类别；第5～8位为4个浮点数，代表目标的2D边界框坐标；第9～11位为3个浮点数，代表目标的尺寸，分别是高、宽、长(单位为m)；第12～14位为3个浮点数，代表目标中心点所处的位置坐标(x,y,z)，该坐标建立在相机坐标系下(单位为m)，坐标轴以相机中心点为坐标原点，正右方为x轴正向，正下方为y轴正向，正前方为z轴正向。本次实验使用x和z作为实验验证的真值，分别代表目标车辆的横向和纵向距离。

本文实验使用的操作系统是Ubuntu 16.04，内存为32 GB，GPU为NVIDIA GeForce GTX 1080Ti，编程环境为Python2.7，深度学习框架为PyTorch 0.4.0版本。使用PyTorch实现的Faster R-CNN目标检测算法[11]进行前期的车辆检测，使用SSD目标检测算法[13]进行车辆关键组件的检测，并将检测阶段和测距阶段进行了融合。

针对驾驶场景中处于不同状态的车辆进行测距分析，如前方车辆转弯、上坡和遮挡。当前方车辆转弯时，本文方法计算的车距是前方车辆相对于当前车辆的纵向和横向的距离，如图14a所示，纵向距离x，横向距离y，该种情况和非转弯的车辆测距情况相同，不影响测距结果；当前方车辆在上坡而当前车辆在水平路面时，如图14b所示，上坡路面角度为α，此时，横向测距结果不受影响，纵向测距结果将发生变化，变为测量值的secα倍，根据《公路工程技术标准》(JTG B01-2003)规定：各级公路的最大纵坡不应大于3%～9%，即当最大纵坡取9%时，secα=1.0040，即误差变化比例为0.004 0，车距为100 m时,误差增加0.40 m；当前方车辆和当前车辆同时处于坡上时，如图14b所示，两者处于同一水平面，测距结果不发生变化；当前方车辆受到遮挡时，如图14c所示，车辆检测阶段会检测不到完整车辆，在车辆组件检测时，如果车辆组件检测结果不完整，则采用车辆矩形框下边中心点作为测距关键点进行车距测量，即相当于采用不进行车辆下边沿估计的方式进行测距，测距误差见5.1节。

Figure 14 Vehicle distance measurement and analysis in different states图14 不同状态下车距测量分析

本文旨在通过深度学习技术来提高车辆视觉测距的精度，所使用的车辆检测方法为Faster R-CNN[11]，该方法为通用的目标检测方法，同其他车距测量方法中需要首先获取车辆外接矩形框的目的相同，本文的创新之处在于基于车辆外接矩形框的检测结果，借助轻量快速的目标检测框架SSD[13]完成对车辆下边沿的估计。测距各阶段用时和算法处理帧率如表1所示。

Table 1 Processing time andprocessing frame rate for each stage

5.1 车辆下边沿对测距误差影响验证

本文对不同纵向物理距离的车辆目标进行分阶段统计测试，总共分为4组进行实验，分别为0～20 m，20～40 m，40～60 m，60～80 m。本次实验的计算规则是分别统计使用下边沿估计和未使用下边沿估计车距测量值与真值之间的差值，即绝对误差。

在实验各阶段，本文提取了符合测量标准的车辆实例，各距离阶段内车辆数量不同，取各阶段测距误差的平均值，实验结果见表2。数量表示各阶段符合测试条件的车辆数，平均误差表示所有距离阶段的车辆测距误差的平均值。从实验结果中可看出，采用下边沿估计的测距精度明显高于未采用下边沿估计的测距精度，其次，纵向测距误差相对于横向测距更大，尤其在未采用车辆下边沿估计的测距方法式中更为明显，而本文方法在横向测距的精度以及稳定性上表现更好。通过实验结果还可以发现，目标纵向距离越大测距误差就会越大，且横向距离和纵向距离的测量误差变化程度会有所不同。如图15所示，在车辆目标的纵向距离逐渐增大的过程中，横向测量误差逐渐增大，且变化非常明显，而纵向测量误差虽然也在增大，但相对稳定，增幅较小。从这里更可以看出，本文方法相对于未使用下边沿估计的方法具有更高的测距精度和稳定性。

Table 2 Influence comparison ofranging error in the lower edge estimation

Figure 15 Variation of ranging error图15 测距误差变化

5.2 本文方法与其他测距方法对比验证

将本文方法和其他测距方法进行对比实验。选取文献[27,28,35,36]中的方法进行实验，同样分成4个不同的距离阶段，分别为0～20 m，20～40 m，40～60 m，60～80 m，根据不同距离阶段内的车辆目标，分别计算测距误差的平均值，包括绝对误差和相对误差，实验结果如表3所示。文献[35]的测距方法只用于对车辆在纵向上的车距测量，该方法在近距离阶段(40 m之内)测距精度较高，在远距离的60～80 m阶段，测距误差变大。文献[27,28,36]的方法可用于纵向和横向上的车距测量。从表3可以看出，随着车辆纵向距离的增大，这几种方法的测距误差也有较大程度的增大，而本文方法随着纵向距离的增大，测距误差并没有出现较大的变化，说明本文方法稳定性更好。无论是分阶段的对比还是平均误差的对比，本文方法明显优于其他几种方法，且测距的精度更高，尤其在横向距离测量上误差更小，表明本文方法针对相邻车道内的车辆目标更加有效。

Table 3 Comparison between thismethod and other ranging methods

6 结束语

本文针对基于单目视觉的车辆测距技术中忽略了车辆与地面相接的下边沿问题，提出了一种基于车辆下边沿估计和逆透视变换的单目视觉测距方法，实现了对前方车辆进行横向和纵向的高精度车距测量。相对于其他测距方法，本文通过下边沿估计模型实现对车辆下边沿的定位，确定更加准确的测距关键点，利用基于点的逆透视变换测距模型进行距离计算。实验结果表明，本文方法的测距精度更高，稳定性更好。在未来的工作中，我们将进一步探索新的车辆下边沿估计模型，在进行车辆下边沿估计时，降低因车辆组件过小而产生的影响，提高算法的鲁棒性，进一步提高车距测量的精度。