不同重连概率的小世界脉冲神经网络抗扰功能研究*

郭 磊，冯 海，石洪溢

(1.天津市生物电工与智能健康重点实验室(河北工业大学),天津 300130;2.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130)

1 引言

随着电磁环境的日益复杂，各种电磁干扰对电子系统造成的不良影响越来越严重，这使得传统电磁抗扰方式不足的问题日渐突出。电磁仿生学[1,2]的概念由此被提出，目的是学习和借鉴生物体的优良特性，以期建立全新防护模式。

生物体在神经系统的调节下呈现出的自适应抗干扰能力是非生物体无法比拟的，而这一能力与突触可塑性的调控密切相关。突触可塑性分为兴奋性和抑制性2种，兴奋性突触可塑性以往是研究的重点[3]，而抑制性突触可塑性的调控作用也逐渐被人所重视。Kleberg等人[4]证明抑制性突触可塑性在兴奋性和抑制性突触电导权值的平衡方面起着至关重要的作用。薛晓丹等人[5]在所构建的反馈神经回路模型中发现，在抑制性突触可塑性的调节下，网络可取得放电率自稳态。神经网络自适应抗扰功能的研究是近年来的热门问题，本课题组针对这一问题的研究现状，开展了基于层级脉冲神经抗扰功能的研究工作[6,7]，前期工作成果有：揭示了生物体的自适应抗干扰能力与突触可塑性机制有关；网络在损伤条件和噪声环境下具有一定的抗扰功能和抗扰范围。王美丽等人[8]在构建的反馈神经回路模型中发现，网络在抑制性突触可塑性的调控下，对外加噪声刺激具有较强的鲁棒性。拓扑结构是网络的关键特性，目前关于神经网络抗扰功能的研究主要是基于层级网络，而复杂网络更符合生物真实性。

大量研究表明，脑网络具有显著的小世界属性[9,10]，小世界网络模型中重连概率参数对其自身网络特性有明显的影响[11]，进一步研究小世界模型的参数对神经网络的抗扰功能的影响具有重要意义。本文构建了兴奋性和抑制性突触可塑性共同调节的小世界脉冲神经网络，研究了不同重连概率的网络在高斯白噪声刺激下的抗扰功能。

2 小世界脉冲神经网络的构建

本文基于小世界网络拓扑，以Izhikevich神经元模型为节点，以突触可塑性模型为连接关系构建了小世界脉冲神经网络。

2.1 小世界网络的生成及其特性分析

WS(Watts-Strogatz)小世界网络的生成算法为：生成节点数目为500的环形规则网络，每一节点与其邻近的各10个节点连接；从第1个节点开始，对其连边以重连概率p进行连接，p取值为0～1。本文通过实验确定生成重连概率p为0.2,0.4,0.6,0.8的小世界网络，基于复杂网络特性理论对比分析各网络拓扑特性。

(1)平均聚类系数。

聚类系数的描述如下所示：

Ci=2ei/(ki(ki-1))

(1)

其中，ei表示节点间实际相互连接的边数，ki表示节点所有相邻节点的个数，ki(ki-1)/2表示节点间最多可能相互连接的边数。平均聚类系数为网络中所有节点聚类系数的平均值，其描述如下所示：

(2)

其中，N表示节点的数目。平均聚类系数表征网络中节点连接的集团化程度和信息传输能力，平均聚类系数越大，网络整体的信息传递能力越强。在图1中，随重连概率的增大，网络平均聚类系数明显减小，说明该系数受重连概率的影响较大。

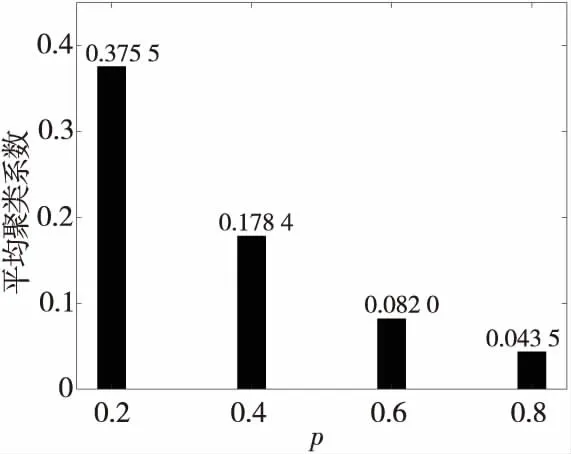
Figure 1 Average clustering coefficient under different rewiring probabilities图1 不同重连概率下的平均聚类系数

(2)平均路径长度。

平均路径长度是表示网络信息传递效率的指标，其值越小代表相应的效率越高，其描述如下：

(3)

其中，dij表示2节点间的距离,V为网络中所有神经元的集合。

在图2中，小世界网络的神经信息传递效率随重连概率的增大有较小幅度的增大，网络的平均路径长度受重连概率的影响较小。

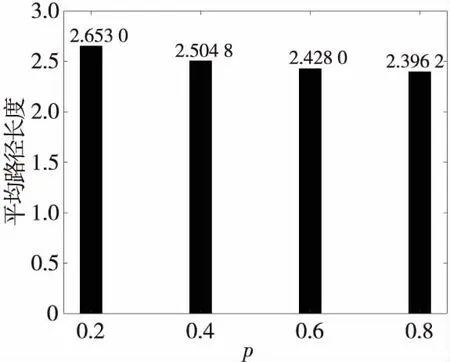
Figure 2 Average path length under different rewiring probabilities图2 不同重连概率下的平均路径长度

(3)全局效率。

全局效率是表示网络信息传递效率的指标，其值越大代表相应的指标越好，其描述如下所示：

(4)

在图3中，小世界网络的神经信息传递效率随重连概率的增大有较小幅度的增大，说明网络的全局效率受重连概率的影响较小。

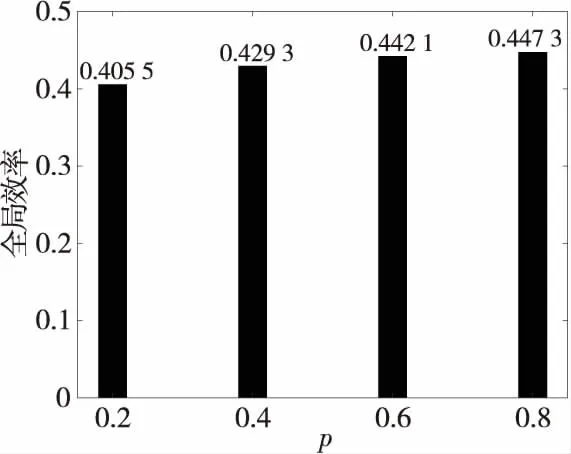
Figure 3 Global efficiency under different rewiring probabilities图3 不同重连概率下的全局效率

(4)小世界属性。

小世界属性可以定量分析小世界网络的属性，其描述如下所示：

σ=γ/λ

(5)

其中，γ表示小世界网络与随机网络平均聚类系数之比，λ表示小世界网络与随机网络的平均路径长度之比。σ>1的网络表示其具有小世界属性。σ值越大代表其相应的属性越强。

Figure 4 Small world attributes under different rewiring probabilities图4 不同重连概率下的小世界属性

在图4中，小世界网络的小世界属性随重连概率的增大明显减小，说明网络的小世界属性受重连概率的影响较大。

小世界网络具有高聚类系数和低平均路径长度的特性，由于各网络拓扑特性受重连概率的影响的不同，从损失较小平均路径长度和全局效率而获得较大的平均聚类系数和小世界属性的角度考虑，较低的重连概率，可较好地满足小世界网络特性。

2.2 Izhikevich神经元模型

Izhikevich神经元模型的优势是适合计算机仿真，且趋近生物真实放电特征，其描述如下所示：

dv/dt=0.04v2+5v+140-u+I，

du/dt=a(bv-u),

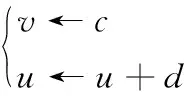
(6)

其中，v表示神经元膜电位；u表示膜电压恢复变量；I表示输入电流和突触电流的总和，a,b,c,d为4个无量纲参数。兴奋性神经元采用规则放电模式RS(Regular Spiking)，其参数设置为：a=0.02,b=0.2,c=-65,d=8，放电特性如图5a所示；抑制性神经元采用低阈值放电模式LTS(Low-Threshold Spiking)，其参数设置为：a=0.02,b=0.25,c=-65,d=2，放电特性如图5b所示。兴奋性和抑制性神经元选择这2种放电模式是因其在生物中常见且具有代表性[12,13]。图5中，横纵坐标分别为仿真时间和神经元膜电压。

Figure 5 Firing mode of Izhikevich neuron图5 Izhikevich神经元放电模式

2.3 突触可塑性模型

突触可塑性模型描述如下：

Isyn=gsyn(t)(V-Vm(t))

(7)

其中，Isyn表示突触电流；gsyn(t)表示突触权值；Vm(t)表示突触后神经元的膜电位；V表示反转电位，兴奋性突触的反转电位VE=0 mV；抑制性突触的反转电位VI=-70 mV。具体调节规律：

(1)当突触前神经元i的动作电位未传递到突触后神经元j时，相应突触权值会发生指数衰减，其描述如下所示：

兴奋性：

(8)

抑制性：

(9)

其中，gex和gin分别表示兴奋性和抑制性突触权值；τex和τin分别表示兴奋性和抑制性突触权值的衰减常数，设定τex=τin=5 ms;t表示时间。

(2)当突触前神经元i的动作电位传递到突触后神经元j时，调控规律描述如下：

兴奋性：

(10)

抑制性：

(11)

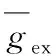
(12)

(13)

其中,Δt表示突触前后神经元放电间隔时间；τ+和τ-表示突触增强和减弱时突触前后神经元放电时刻间隔范围，τ+=τ-=20 ms；A+和A-为兴奋性突触电导在增强和减弱时的最大修正值；B+和B-为抑制性突触电导在增强和减弱时的最大修正值。A+=0.1,A-=0.105；B+=0.02,B-=0.03。

本文以重连概率分别为0.2,0.4,0.6,0.8，节点规模均为500的WS小世界网络拓扑，以Izhikevich神经元模型为节点，基于兴奋性和抑制性突触可塑性模型构建4个网络拓扑的脉冲神经网络。依据神经解剖学实验结果，网络中兴奋性神经元和抑制性神经元的比例为4∶1[14]。

3 高斯白噪声刺激下网络的抗扰功能分析

本文以放电率和膜电位相关性作为抗扰指标对比分析了不同重连概率的小世界脉冲神经网络的抗扰功能。

3.1 高斯白噪声

现实生活中如雷达和通讯系统等电子系统中的噪声形式多为高斯白噪声，因此以高斯白噪声为噪声环境研究抗扰功能具有重要的现实意义。高斯白噪声ξ(t)满足：

〈ξ(t)〉=0

(14)

〈ξi(t),ξj(t′)〉=Dδijδ(t-t′)

(15)

其中，ξi(t),ξj(t′)为神经元i,j的噪声干扰项，D为噪声强度，当i=j(t=t′)时，δij=1(δ(t-t′)=1);否则，δij=0(δ(t-t′)=0)。高斯白噪声为电流刺激，实验时将ξ(t)施加到式(6)的电流部分得到高斯白噪声下脉冲神经网络模型。

3.2 不同重连概率的网络抗扰功能对比性分析

3.2.1 基于放电率网络抗扰功能的分析

放电率为单位时间内神经元脉冲发放次数。本文中的放电率取网络中的平均值。为了定量计算干扰前后放电率的变化，引入放电率的相对变化率，其描述如下所示：

δ=((fj-fi)/fi)*100%

(16)

其中，fi表示干扰前网络的放电率，fj表示干扰后网络的放电率，δ表示干扰前后放电率的相对变化率。通过计算干扰前后放电率的相对变化率分析不同重连概率下小世界脉冲神经网络抗扰功能。

以放电率作为不同重连概率下的小世界脉冲神经网络的抗扰指标分析网络的抗扰功能，对重连概率分别为0.2,0.4,0.6,0.8的小世界脉冲神经网络中的所有神经元加入强度分别为1 dBW,5 dBW,10 dBW,15 dBW,20 dBW的高斯白噪声，该噪声强度是通过实验取得的，仿真时间为1 000 ms，不同强度的高斯白噪声刺激下4个网络拓扑结构的脉冲神经网络的放电率和放电率的相对变化率的变化趋势如图6所示。

在图6a和图6b中，横坐标表示噪声强度，纵坐标分别表示小世界脉冲神经网络的放电率和放电率的相对变化率。其中，菱型折线、方型折线、十字型折线、三角型折线分别表示重连概率为0.2,0.4,0.6,0.8的网络放电率随高斯白噪声的变化情况。由图6a可知，随高斯白噪声强度的逐步增加，各网络的放电率基本呈现上升趋势，说明噪声的强度越大对网络的作用越强。由图6b可知：(1)在一定噪声强度内，各网络的放电率的相对变化率都较小，说明各网络对此强度范围内噪声的抑制作用较强；超过一定的范围后，放电率的相对变化率较大，说明各网络对此强度范围内噪声的抑制作用变差。(2)当噪声强度为1 dBW,5 dBW, 20 dBW时，重连概率为0.2的网络的放电率的相对变化率最低；当噪声强度为10 dBW, 15 dBW时，重连概率为0.2的网络的放电率的相对变化率同样较低，说明重连概率为0.2的网络抗扰功能优于其他重连概率的网络的。

Figure 6 Firing rate varing with the intensity of white Gauss noise图6 放电率随高斯白噪声强度变化

3.2.2 基于膜电位相关性网络抗扰功能的分析

膜电位相关性可以反映干扰前后神经元膜电位的相似程度。本文通过相关系数计算膜电位相关性，数学表达如下所示：

(17)

其中，xi和xj是高斯白噪声干扰前后网络中所有神经元膜电位的平均值，[t1,t2]为仿真时长。

本文通过分析相关系数ρ(τ)的大小来分析网络的抗扰功能，ρ(τ)越大说明干扰前后神经元膜电位的近似程度越高，其抗扰功能越强。

本文以膜电位相关性作为脉冲神经网络的抗扰指标分析网络的抗扰功能，在计算膜电位相关性中干扰前后的膜电位取干扰前后整个网络中的平均值。对重连概率分别为0.2,0.4,0.6,0.8网络的所有神经元加入强度分别为1 dBW,5 dBW,10 dBW,15 dBW, 20 dBW的高斯白噪声，该噪声强度是通过实验取得的，仿真时间为1 000 ms，不同强度的高斯白噪声刺激下4个网络拓扑结构的脉冲神经网络的的膜电位相关性的变化趋势如图7所示。

Figure 7 Correlation between membrane potential varing with the intensity of white Gauss noise图7 膜电位相关性随高斯白噪声强度的变化

在图7中，横纵坐标分别表示高斯白噪声强度和小世界脉冲神经网络膜电位相关性。其中，菱型折线、方型折线、十字型折线、三角型折线分别表示重连概率为0.2,0.4,0.6,0.8的小世界脉冲神经网络膜电位相关性随高斯白噪声的变化情况。由图7可知：(1)随高斯白噪声刺激强度的增大，各网络的膜电位相关性基本呈下降趋势，说明噪声的强度越大对网络的作用越强。(2)在一定噪声强度范围内，不同重连概率的小世界脉冲神经网络的膜电位相关性较大，说明网络对此强度范围内噪声的抑制作用较强；超过一定的范围后，各网络的膜电位相关性较小，说明各网络对此强度范围内噪声的抑制作用变差。(3)在不同重连概率的小世界脉冲神经网络对比中，重连概率为0.2,0.8的小世界脉冲神经网络的膜电位相关性基本相当且高于其他重连概率的网络，说明以膜电位作为抗扰指标，重连概率为0.2,0.8的网络的抗扰功能优于其他重连概率的网络的。

综上所述，基于放电率和膜电位相关性的抗扰指标对比均得出以下一致结论：(1)重连概率的改变对脉冲神经网络的抗扰功能有影响；(2)最低重连概率0.2的网络的抗扰功能最优，是由于该网络的小世界网络特性最显著。

4 结束语

本文基于复杂网络特性理论对比分析了不同重连概率的小世界网络的拓扑特性；以放电率的相对变化率和膜电位相关性作为抗扰功能的指标，对比分析了4个重连概率的小世界脉冲网络在高斯白噪声刺激下的抗扰功能。实验结果表明，重连概率对平均路径长度和全局效率值影响较小，而对平均聚类系数和小世界属性的影响较大，即较低重连概率的小世界网络损失较小的平均路径长度和全局效率而获得较大的平均聚类系数和小世界属性的角度能够较好地满足小世界网络特性。针对一定强度的高斯白噪声刺激，基于不同重连概率所构建的小世界脉冲神经网络均呈现了一定的抗扰能力，且具有较高聚类系数和较低平均路径长度的脉冲神经网络的抗扰功能更优良。基于突触可塑性的突触权值调节机制是脉冲神经网络抗扰功能的基础，重连概率作为小世界网络的重要参数，较低的重连概率可使小世界网络具有显著小世界特性，显著的小世界特性使该网络拓扑的脉冲神经网络具有优良抗扰功能。下一步本课题组将开展基于FPGA脉冲神经网络构建及抗扰功能的硬件实现的研究工作。