乔纳金苹果的应力松弛和蠕变特性与其品质相关性分析
2020-07-27张彩霞丛佩华
杨 玲,田 义,张彩霞,丛佩华,*
(1.农业部园艺作物种质资源利用重点实验室,辽宁 兴城 125100;2.中国农业科学院果树研究所,辽宁 兴城 125100)
苹果(Malus domestica)是我国大众消费果品,在果品贮藏、运输、加工过程中,由于食品的组成及内部结构决定了食品物质的流变特性,而流变特性和组成分子特性与微观结构又决定了食品的质地特性[1]。所以果品的生理组织结构、生化成分变化及流变损伤效应等的交叉影响,不仅使果品的外观受到影响,而且果实的食用性和商品性也大大降低。因此,研究苹果的流变特性不仅可以为完善果实质地品质评价体系提供理论支持,还为果品的加工机械设计提供依据,也为实现果品快速和精确量化检测提供数据支持。
果蔬的流变特性存在于果蔬生产的各个环节,不仅为采后处理加工提供理论依据,并可以通过流变特性测定预测评价果实的质地品质。苹果属黏弹性固体物料,其力学特性与果实本身的黏弹性密切相关,而生物组织力学特性主要受细胞结构、水分和化学物质成分含量的影响,因此果实的流变特性与化学成分含量和质地具有一定的相关性。目前国内外已有研究表明果实流变特性与其营养成分指标具有相关性。孙骊等[2]和李小昱等[3]研究指出,苹果的贮藏损伤可用蠕变特性参数来描述。方媛等[4]通过对红富士蠕变特性研究探讨蠕变参数与苹果质地和营养成分含量的相关性。王善荣等[5]对水蜜桃的机械损伤和品质相关性进行研究。陆秋君等[6]研究揭示了常温贮藏过程中番茄的4 项蠕变特性参数与其内部品质指标(糖度和pH 值等)的相关性。杨晓清等[7]、王芳[8]和宋晓宇[9]建立了果实力学特性与化学品质指标间的多元回归模型,通过力学指标用于预测化学品质。郭文斌[10]建立了力学特性参数(弹性模量、破坏能、黏性系数等)与马铃薯淀粉含量的回归方程,用力学参数来预测马铃薯淀粉含量。熊秀芳[11]研究了红富士苹果抗压性能与糖度、酸度、水分的相关性,并进行了回归分析预测。Afkari-Sayyah 等[12]研究发现,苹果蠕变特性参数与其可滴定酸度、可溶性固形物含量显著相关。Nieto 等[13]研究发现,苹果应力松弛时间与其可溶性固形物含量显著相关。Winisdorffer 等[14]研究了6 种苹果果肉细胞质水分、化学成分等与流变特性参数之间相关性,结果表明细胞壁阿拉伯糖、细胞质水分等与杨氏模量有关,木糖、半纤维素等与阻尼系数有关。这些研究表明,通过压缩测量获得果实的流变特性参数是有望实现对果实可溶性固形物含量、可滴定酸含量等主要营养成分指标的快速检测。
乔纳金苹果具有早果丰产、风味酸甜适度、汁液丰富、肉质松脆等特性,遍及我国主要苹果产区,但贮藏性中等,比早熟苹果嘎拉等耐贮,比晚熟苹果红富士耐贮性稍差。为实现苹果果实多种营养成分指标高效准确的检测,本研究以乔纳金苹果为试材进行流变特性测试,分析蠕变特性、应力松弛特性参数与TPA质地参数、乔纳金苹果果肉可溶性固形物、原果胶等的相关性,并构建了这些指标的数学预测模型,为预测果品质构特性和口感品质提供数据支持。
1 材料与方法
1.1 材料与设备
1.1.1 材料与试剂
乔纳金苹果果实于2015 年采自辽宁省葫芦岛市双树乡果园,于果实9 成熟时适时采收,选取大小均匀、成熟度相近的苹果果实,随机采摘果实各140 个,备用。
无水乙醇、95%乙醇、咔唑购于国药集团化学试剂有限公司,硫酸购于天津市科密欧化学试剂有限公司。
1.1.2 仪器与设备
TMS-PRO 型质构仪,GMK-701AC 型数字糖度计,HH-6 数显恒温水浴锅、UV-1800 型紫外分光光度计。
1.2 方法
1.2.1 试验方案设计
将采收的苹果置于室温下保鲜袋内(未扎口)贮藏,6 次试验共从中选取形状相近、无病虫害的果实70 个作为试验果。试验环境温度为(20±2)℃,空气相对湿度为 65%±5%,果实分别在贮藏 0、5、10、15、20、25 d 分6 次取样测试,每次分别随机取样5 个果实用于质地参数测定。每个果实先切成两半,分别在果实中部切取2 cm×2 cm×2 cm 大小共4 块果肉,一次取20 个大小相同的果肉共重复20 次。
1.2.2 乔纳金苹果果肉流变分析
快速切取果肉置于质构仪平板上,然后利用质构仪圆形探头(直径为75 mm)对苹果果肉进行蠕变、松弛测试。蠕变测试参数为:测试速度60 mm/min、起始力2 N、设定压力10 N、压缩时间30 s。测定参数为位移、时间、压力。松弛测试参数为:测试速度60 mm/min,起始力2 N,形变百分量为3%。测定参数为应力松弛的力、位移、时间。
1.2.3 乔纳金苹果果肉蠕变数学模型
据国内外文献[15-18]报道,农业物料的蠕变特性一般可以用伯格斯模型(Burger’s Model)表示。根据本试验的蠕变特性曲线和所测定的试验数据,苹果的蠕变加载过程选用四元件Burger’s 模型描述。
加载过程变形量D(t)随时间t的变化公式为:
D(t)=F0/E1+F0*t/η1+F0*[1-exp(-t/τ)]/E2
式中,D(t)为变形量,mm;F0为定载荷,N;E1为初始弹性系数,N·mm-1;E2为延迟弹性系数,N·mm-1;τ 为延迟时间,s;τ=η2/E2;η1、η2为黏性系数,N·s·mm-1;t为时间,s。
通过以上四元件伯格斯模型(Burger’s Model)方程对试验数据进行非线性回归分析(Non-liner Regression Analysis),由SPSS 统计软件通过换算和计算求得参数初始弹性系数E1、延迟弹性系数E2、延迟时间τ、黏性系数η1、黏性系数η2,拟合方程的决定系数均在0.981 以上,进而确定苹果蠕变模型的参数指标。
1.2.4 三种苹果果肉松弛数学模型
据国内外文献[19-21]报道可知,能分析反映应力松弛曲线的方法有4 种。根据本试验的松弛特性曲线和试验数据的拟合,选用三参数的广义Maxwell 模型进行数学模型的非线性回归分析的曲线拟合。广义麦克斯韦模型经常用于黏弹性物料应力松弛曲线的拟合分析。模型方程为:
E(t)=Ee+E1′exp(-t/T)
式中,E(t)为任意时刻瞬时弹性模量,MPa;E1′为衰变弹性模量,MPa;Ee为平衡弹性模量,MPa;T为应力松弛时间,T=η/E1′(s),η=T×E1′,η 为阻尼体黏滞系数(N·s/mm)。
在t=0 时,由上式可得零时弹性模量为:
E0=E(t=0)=E1′+Ee
通过模型方程对试验数据进行非线性回归分析,由 SPSS 统计软件求出参数常量E1′、Ee、E0、T、η,拟合方程的决定系数均在0.943 以上,进而确定苹果应力松弛特性模型参数。对蠕变、松弛模型参数和TPA 指标、化学成分含量进行相关性分析并用逐步回归分析法进行回归分析,建立苹果各项品质的预测模型。
1.2.5 可溶性固形物含量的测定
使用GMK-701AC 数字糖度计测定。
1.2.6 原果胶含量的测定
参照赵志磊[22]方法,每个处理选取大小均匀一致的5 个果实,3 次重复。取5 g 果肉置于50 mL 刻度离心管中,加35 mL 的无水乙醇,在85 ℃水浴中加热10 min,充分振荡、冷却,再加无水乙醇使总体积接近50 mL,在4 000 r/min 下离心15 min,弃去上清液。加入95%乙醇50 mL,在沸水浴中加热30~40 min 除去糖分及其他物质。用滤液过滤,弃去废液,沉淀放入原烧杯中,加水40 mL 在水浴锅上加热50 ℃,保持30 min 以溶解果胶。过滤,用少量水洗涤滤纸和沉淀。滤液定容至50 mL 为可溶性果胶。
沉淀放入原烧杯中,加入0.5 mol/L 硫酸100 mL,在沸水浴中加热1 h 以水解原果胶,冷却后移入100 mL容量瓶中,加水定容至100 mL,此为原果胶测定液。
吸取可溶性果胶液和原果胶液各0.1 mL,加入到20 mL 刻度试管中,然后在加入0.9 mL 蒸馏水于试管中各加入浓硫酸6 mL,沸水加热20 min,冷却后加入0.15%咔唑乙醇0.2 mL,于暗处放置1.5 h,在530 nm波长下比色测光密度。
1.2.7 数据处理
使用SPSS 统计软件进行数据处理,Excel 2007软件进行作图。
2 结果与分析
2.1 乔纳金苹果果肉货架期间蠕变参数分析
2.1.1 乔纳金苹果果肉货架期间蠕变特性参数的变化趋势
蠕变试验是对测试样品突然施加一定的载荷并保持常值,测定变形(应变)与时间的函数关系。加载力限定在线性黏弹性范围内,对物料不造成机械损伤。当乔纳金苹果果肉受到蠕变加载力瞬间,瞬时弹性系数E1发挥作用,产生弹性形变,E2受到黏性系数η2的制约,加载后并不迅速产生变形,而是随着时间的增加缓慢产生变形,E1、E2卸载后变形都能迅速恢复。由图1 可见,乔纳金苹果果肉初始弹性系数E1、延迟弹性系数E2在货架期0~25 d 变化趋势基本一致,大体呈下降趋势,货架5 d 时比初始值稍高;25 d和20 d 时,E1和E2变化不大。这说明乔纳金苹果果肉在采后5 d 后果肉弹性有所增加,有可能果肉细胞壁物质降解为可溶性物质,增加了细胞膨压,细胞间弹性降低。随着蠕变加载时间的增长,果肉产生黏性流动变形,分为两部分:黏性系数η1为麦克斯韦体内的独立黏性产生的变形,卸载后此部分变形不恢复;另一部分黏性系数η2是开尔文体内的黏性,这部分变形在加载力卸载后也会逐渐恢复。但乔纳金果肉黏性系数η1和黏性系数η2在货架期0~25 d 是变化趋势和E1、E2相似,都大体呈下降趋势。黏性系数η1在货架5 d 时稍有升高,η2则呈略微下降趋势,25 d 相比20 d 时略有升高。在货架期内,乔纳金果肉的弹性和黏性都呈下降趋势,20~25 d 时可能由于细胞壁物质降解到一定程度,细胞壁膨压增大,果肉细胞壁弹性和黏性稍有升高或不变。延迟时间τ 在采后5 d 后有所下降,10~15 d 略有增加。
2.1.2 蠕变参数与TPA 指标及果肉化学成分含量相关性和回归性分析
由表1 可见:蠕变参数延迟弹性系数E2与初始弹性系数E1之间呈极显著正相关(P<0.01),相关系数为0.969;黏性系数η1与初始弹性系数E1和延迟弹性系数E2之间呈极显著正相关(P<0.01),相关系数分别为0.923 和0.974;黏性系数η2与初始弹性系数E1之间呈显著正相关(P<0.05),相关系数分别为0.910,与延迟弹性系数E2、黏性系数η1之间呈极显著正相关(P<0.01),相关系数分别为0.952 和0.929。以上结果说明了乔纳金苹果在货架期间的弹性与黏性紧密相关,是果肉细胞与细胞之间共同作用的结果。果肉硬度与初始弹性系数E1、延迟弹性系数E2、黏性系数η1和黏性系数η2之间呈极显著正相关(P<0.01),相关系数分别为 0.953、0.995、0.966 和0.933,说明了乔纳金苹果果肉硬度与黏弹性紧密相关,即乔纳金的果肉的软硬程度与黏弹性之间呈极显著相关(P<0.01)。内聚性与初始弹性系数E1、延迟弹性系数E2、黏性系数η1、果肉硬度之间呈显著正相关(P<0.05),相关系数分别为 0.815、0.895、0.897、0.914;与延迟时间τ 之间呈显著负相关(P<0.05),相关系数为-0.860。弹性与初始弹性系数E1、延迟弹性系数E2、黏性系数 η1之间呈显著正相关(P<0.05),相关系数分别为0.825、0.899、0.880,弹性与果肉硬度、内聚性之间呈极显著相关(P<0.01),相关系数分别为0.921 和0.996;与延迟时间τ 之间呈显著负相关(P<0.05),相关系数为-0.876。这些参数都反映了果肉细胞间组织结构与分子间结合力的大小,而且都能说明果肉组织结构状态。咀嚼性与初始弹性系数E1、延迟弹性系数E2、黏性系数 η1、黏性系数 η2、果肉硬度、内聚性和弹性之间呈极显著正相关(P<0.01),相关系数分别为 0.932、0.980、0.967、0.883、0.989、0.959和0.960。咀嚼性反映了果实对咀嚼的抵抗力,间接表明果肉细胞组织结构与分子间结合力的大小,其与蠕变参数弹性系数和黏性系数的显著相关性更证实了TPA 参数与蠕变参数都能反映货架期乔纳金苹果果实的质地性状。原果胶与蠕变参数初始弹性系数E1、延迟弹性系数E2、黏性系数η1、黏性系数η2和咀嚼性之间呈显著正相关(P<0.05),相关系数分别为0.847、0.915、0.886、0.907 和 0.901;与果肉硬度之间呈极显著正相关(P<0.01),相关系数为0.937。上述结果进一步说明果肉蠕变黏弹性变化和TPA 参数变化都与果肉细胞壁不溶性原果胶降解为可溶性果胶有关。可溶性固形物与延迟弹性系数E2、硬度、弹性、咀嚼性之间呈显著正相关(P<0.05),相关系数分别为0.863、0.875、0.819 和0.876;与初始弹性系数E1之间呈极显著正相关(P<0.01),相关系数为0.921;与延迟时间τ 之间呈显著负相关(P<0.05),相关系数为-0.825。乔纳金果实货架期品质变化与果肉质地的变化显著相关,是同步进行的。
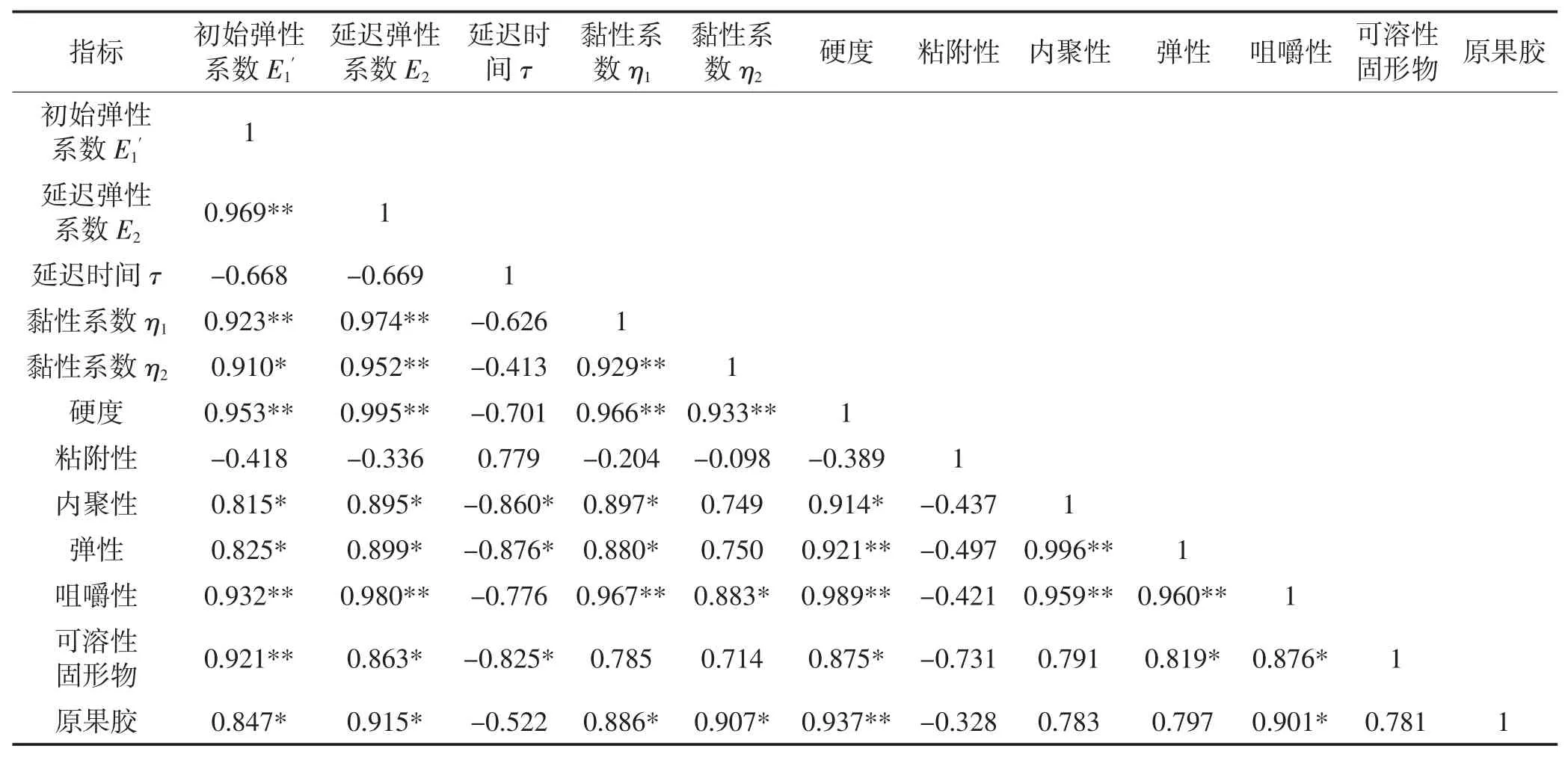
表1 蠕变参数与TPA 指标、果肉化学成分含量相关性分析Table1 Correlation analysis of creep parameters with TPA index and pulp chemical composition
由以上数据分析可知,可溶性固形物、原果胶、TPA 主要质地指标(硬度、内聚性、弹性、咀嚼性)与蠕变参数(初始弹性系数E1、延迟弹性系数E2、黏性系数 η1、黏性系数 η2、延迟时间 τ 等)之间呈显著相关性,现通过蠕变特性参数对以上各指标进行预测,以蠕变特性参数为自变量,以可溶性固形物、原果胶、TPA 主要质地指标(硬度、内聚性、弹性、咀嚼性)为因变量,通过SPSS 软件进行逐步回归分析,剔除F值显著水平大于0.05 的变量,预测一元线性回归模型。
从表2 中可以看出:可溶性固形物、原果胶、TPA指标(硬度、内聚性、弹性、咀嚼性)由蠕变参数构成的预测模型,决定系数R2均达到0.8 以上,且均具有统计学意义(P<0.05),TPA 参数(硬度、内聚性、弹性、咀嚼性)指标预测模型都存在且仅存在变量延迟弹性系数E2,说明他们仅与弹性元件有关,而黏性变形并不对预测结果产生显著影响。而可溶性固形物仅与初始弹性系数E1有关,而原果胶则与黏性元件η1有关。

表2 蠕变参数与化学成分含量和TPA 指标的回归分析结果Table 2 Regression analysis of chemical components and TPA indexes by creep parameters
2.2 乔纳金苹果果肉货架期间松弛参数分析
2.2.1 乔纳金苹果果肉货架期间松弛特性参数的变化趋势
应力松弛加载力造成物料变形,随着时间增长果肉内部抵消应力达到平衡状态。当加载力加载到果肉上时,应力随着时间不断衰减,直至趋于平衡达到平衡应力σe时,初始应力载荷σ0与平衡应力σe的差值σ1对应的弹性元件上的弹性模量为衰变弹性模量E1′,平衡应力 σe对应的弹性元件上的弹性模量Ee,称为平衡弹性模量Ee[10]。由图2 可知,乔纳金苹果果肉衰变弹性模量E1′在货架期0~25 d 内大体呈缓慢下降趋势,但在10 d 后衰变弹性模量E1′变化不大,这说明乔纳金苹果果肉松弛初始弹性在0~10 d 呈下降趋势,10 d 之后则基本变化不大。平衡弹性模量Ee与零时弹性模量E0在0~25 d 一直呈下降趋势,说明果肉弹性在货架期受果肉组织细胞的细胞壁、细胞质等生物组织结构变化的影响,果肉细胞膨压与细胞壁弹性相互结合、共同作用,表现出果肉的黏弹特性的统一。这也充分证实了应力松弛能够描述果肉在细胞水平上的变化特征。在应力松弛过程中,应变ε 保持常值时,应力衰减到初始应力的1/e 或初始应力的36.8%时所需的时间。
乔纳金苹果果肉松弛时间Ts在0~10 d 时稍有升高,10~25 d 略有下降。应力松弛流变学模型中黏性元件阻尼器的黏性系数与果肉中液体黏度有关,黏滞系数η 在货架期呈下降趋势,说明果肉在货架期内黏性下降。在货架20 d 与25 d 时,松弛参数衰变弹性模量E1′、平衡弹性模量Ee、零时弹性模量E0、松弛时间Ts和黏滞系数η 均变化不大。
2.2.2 松弛参数与TPA 指标及果肉化学成分含量相关性和回归性分析
由表3 可知:松弛参数平衡弹性模量Ee与衰变弹性模量E1′之间呈显著正相关(P<0.05),相关系数为0.849;零时弹性模量E0与衰变弹性模量E1呈显著正相关(P<0.05),相关系数为0.914,与平衡弹性模量Ee呈极显著正相关(P<0.01),相关系数为0.990;黏滞系数η 与衰变弹性模量E1′之间呈显著正相关(P<0.05),相关系数为 0.831,与平衡弹性模量Ee、零时弹性模量E0之间呈极显著正相关(P<0.01),相关系数分别为0.981 和0.971(P<0.01)。这说明了乔纳金苹果果肉松弛开始时弹性模量越大,松弛过程中应力衰减越多,达到平衡后,试样果肉所残留的弹性模量越大。Ballabio 等[23]研究表明,苹果质构参数与流变特性参数之间存在相关性。TPA 果肉硬度与松弛参数平衡弹性模量Ee、黏滞系数η 之间呈极显著正相关(P<0.01),相关系数分别为 0.941、0.969;与零时弹性模量E0、松弛时间Ts之间呈显著正相关(P<0.05),相关系数分别为0.902 和0.890,说明乔纳金果肉质地硬度与松弛流变特性黏弹性参数存在显著相关性。内聚性与平衡弹性模量Ee、松弛时间Ts、黏滞系数η、果肉硬度呈显著正相关(P<0.05),相关系数分别为0.841、0.877、0.829 和 0.914;弹性与蠕变参数平衡弹性模量Ee、松弛时间Ts、黏滞系数η 之间呈显著正相关(P<0.05),相关系数分别为 0.858、0.852、0.842,与果肉硬度、内聚性之间呈极显著正相关(P<0.01),相关系数分别为0.921 和0.996。以上结果说明TPA 果肉内聚性、弹性与松弛黏弹性之间存在显著相关性,都能很好地反映乔纳金苹果果肉的质地品质特性。咀嚼性与平衡弹性模量Ee、黏滞系数η、果肉硬度、内聚性和弹性之间呈极显著正相关(P<0.01),相关系数分别为 0.938、0.949、0.989、0.959 和 0.960,与零时弹性模量E0和松弛时间Ts之间呈显著正相关(P<0.05),相关系数分别为0.889 和0.896。陆秋君等[6]研究了番茄货架期四项蠕变特性参数与糖度、pH 等品质指标的相关性。Kaur 等[24]和 López-Perea 等[25]研究表明,马铃薯应力松弛特性参数和淀粉含量有显著相关性。这进一步证实应力松弛特性参数与食品化学成分含量有密切相关性。可溶性固形物与衰变弹性模量E1′、果肉硬度、弹性、咀嚼性之间呈显著正相关(P<0.05),相关系数为 0.855、0.875、0.819 和 0.876,与平衡弹性模量Ee、零时弹性模量E0、黏滞系数η 之间呈极显著正相关(P<0.01),相关系数分别为0.979、0.976、0.926。原果胶与平衡弹性模量Ee、零时弹性模量E0、咀嚼性之间呈显著正相关(P<0.05),相关系数分别为0.878、0.875 和0.901,与黏滞系数η 和硬度之间呈极显著正相关(P<0.01),相关系数分别为0.946 和0.937。

表3 松弛参数与TPA 指标、果肉化学成分含量相关性分析Table 3 Correlation analysis of relaxation parameters with TPA index and pulp chemical composition
由表4 数据分析可知,可溶性固形物、原果胶、TPA 主要质地指标(硬度、内聚性、弹性、咀嚼性)与松弛参数(平衡弹性模量Ee、衰变弹性模量E1、零时弹性模量E0、松弛时间Ts、黏滞系数η 等)之间呈显著相关性,现通过松弛特性参数对以上各指标进行预测,以松弛特性参数为自变量,以可溶性固形物、原果胶、TPA 主要质地指标硬度、内聚性、弹性、咀嚼性为因变量,通过SPSS 进行逐步回归分析,剔除F值显著水平大于0.05 的变量预测的一元线性回归模型,回归方程经方差分析表明模型均具有意义(模型决定系数R2>0.7),均达极显著或显著水平。
2.3 乔纳金苹果果肉流变学蠕变、松弛特性参数主成分分析
为了简化乔纳金苹果果肉质地评价指标及检验各成分在果肉流变学特性评价中所占比重,对乔纳金苹果蠕变、松弛特性参数指标进行主成分分析,见表5。乔纳金主成分的累积贡献率达到了93.28%,其中第一主成分占82.871%,是主要评价成分因子。乔纳金第一主成分除了蠕变参数延迟时间τ 成分得分系数较小外,其余9 个蠕变、松弛流变学特性参数成分得分系数相差不大;第二主成分贡献率为10.409%,成分得分系数绝对值较大的是衰变弹性模量E1′、松弛时间Ts。

表4 松弛参数与营养成分含量和TPA 指标的回归分析结果Table 4 Regression analysis of chemical components and TPA indexes by relaxation parameters
由以上研究表明,乔纳金苹果果肉都具有黏弹性,由黏性因子贡献率和弹性因子贡献率可以看出,苹果果肉质地兼具有黏性和弹性,且贡献率均等。

表5 主成分的特征向量、特征值、贡献率及累计贡献率Table 5 Eigenvector,eigenvalue,contribution and accumulative contribution rate of principle components
3 讨论与讨论
乔纳金苹果果肉蠕变参数初始弹性系数E1、延迟弹性系数E2、黏性系数 η1、η2;松弛参数衰变弹性模量E1′、平衡弹性模量Ee、零时弹性模量E0和阻尼体黏滞系数η 在货架期内大体呈下降趋势,这与吴洪华[26]、孙国辉[27]研究的梨、油桃的蠕变、松弛参数变化趋势一致。蠕变参数延迟时间τ 略有升高,应力松弛时间T则是先升高后下降。这个变化趋势和以上两个研究略有不同,可能是品种不同造成的变化趋势不同。
国内外已有研究表明,具有黏弹性体果蔬的流变学参数与果实品质紧密相关。杨晓清[28]、宋晓宇[9]、郭文斌[10]研究了厚皮蜜瓜、马铃薯各流变机械特性参数与品质指标呈显著相关。王芳[8]、Afkari-Sayyah 等[12]、Nieto 等[13]通过蠕变参数预测总糖、pH、可溶性固形物、含水量等,并建立多元线性回归方程。可溶性固形物指细胞液内所含的可溶性糖类、果胶、氨基酸、维生素等,其中以糖类为主,对果实品质的主要体现在其营养和口味上,是衡量果实品质的重要指标。原果胶是存在于细胞壁的一种非溶性果胶质,构成相邻细胞中间层粘结物,使植物组织细胞紧紧粘接在一起。因此黏弹性体苹果可溶性固形物和原果胶是与果肉流变特性密切相关的化学物质。通过逐步回归分析法,建立了以TPA 质构参数、可溶性固形物、原果胶为因变量,以蠕变、松弛参数为自变量的一元线性预测回归模型。由TPA 质构参数弹性、咀嚼性预测回归模型可知,弹性和咀嚼性都与蠕变参数延迟弹性系数E2和松弛参数平衡弹性模量Ee有关,这说明了弹性、咀嚼性与流变学模型参数中弹性元件有关,而与黏性元件无关。由蠕变、松弛参数与可溶性固形物的回归分析结果可知,与蠕变参数有关的预测模型仅与弹性元件初始弹性系数E1有关,与松弛参数有关预测模型仅与平衡弹性模量Ee有关,进一步说明可溶性固形物预测模型不管是松弛还是蠕变流变学特性,都仅与弹性元件有关。而黏性元件并不对预测结果产生影响。原果胶预测模型在与蠕变参数有关的模型中与黏性系数η1有关,在与松弛参数有关的预测模型中则与黏滞系数η 有关,这也说明了原果胶预测模型仅与流变学参数中黏性元件有关,而弹性元件并不对预测结果产生显著影响。
以上研究结果表明,乔纳金苹果果肉黏性因子和弹性因子与相关营养成分都具有较密切关系,能够综合反映其内部品质特性。通过乔纳金苹果的蠕变、松弛参数主成分分析,揭示了各蠕变、松弛参数在果肉流变学特性评价中的贡献率,说明果肉蠕变、松弛中黏性、弹性参数贡献率均等,乔纳金苹果果肉在货架期兼具黏性和弹性。
本研究通过探讨乔纳金流变学特性参数与化学成分和TPA 质地参数之间的相关性,构建了流变模型参数预测苹果质构参数和化学成分含量的数学关系模型,这不仅为苹果使用流变特性参数评价预测苹果品质奠定了理论基础,还为高效快速检测、预测苹果内在品质开辟了一条新途径,对苹果的贮藏、保鲜、运输加工均具有重要意义。
