弹道导弹弹道交叉碰撞概率精确计算方法

王政伟,梁 波,谢 鹏

(中国电子科技集团公司第二十八研究所,江苏 南京 210007)

鉴于美国的“发射即摧毁”能力,在弹道导弹大规模集群作战过程中,如图1所示,部队需要在最短的时间内完成导弹的发射,然后，快速进行撤收和隐蔽,使作战部队暴露时间最少,提升其作战生存概率。但是,大规模的导弹集中发射时并不能在同一时间进行点火发射,必须要通过保持一定的发射间隔来避免发射与飞行过程中弹间的相互气动影响和交叉碰撞问题[1-2]。目前,在大规模火力分配过程中,通常只是将武器飞行弹道进行平面投影[3],进行平面交叉分析,来确定最小发射时间间隔,这种方法忽略了导弹飞行高度影响,无法准确计算飞行器间的真实距离,会导致火力分配后的发射间隔大大增加。在导弹飞行过程中,还存在由于各种随机误差引起飞行理论偏差[4-7],导弹飞行实际位置与理论弹道轨迹位置存在概率分布误差,理论弹道位置不能作为实际作战过程中弹道交叉的直接判据。本文利用导弹间各自的位置矢量和速度矢量,并引入了导弹位置误差协方差矩阵计算方法[8-11],将问题转换为求解导弹位置概率分布下弹间的空间交叉碰撞概率问题,并对三维空间下弹间交叉碰撞概率的求解过程进行了推导,为弹道导弹集群发射时序确定问题提供了最优化解决方法。

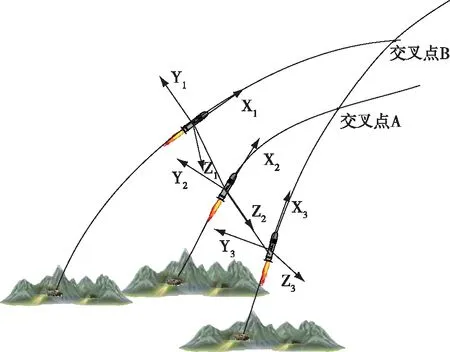
图1 导弹集群发射中的弹道交叉

1 弹道交叉问题分析与建模

1.1 问题分析

弹道交叉是指导弹在飞行过程中距离过近时容易相互产生气动、电磁干扰甚至物理碰撞的情况,严重影响了导弹飞行安全。本次进行三维空间建模时遵循以下假设:

1)在导弹飞行主动段和再入段主要考虑气动、电磁干扰,导弹间相互干扰简化为弹间需保持一定的安全距离来避免干扰和碰撞。

2)导弹被动段飞行一般处于真空环境,主要考虑弹间的物理碰撞问题。

3)导弹飞行过程中,其位置误差是以理论弹道位置为中心的球状空间分布。

1.2 导弹运动模型

已知导弹的理论轨道方程[9]可表示如下。

其中,t为导弹飞行时间,X、Y、Z分别为导弹在空间中的位置变量。

而在实际导弹的飞行过程中,由于天气、导弹本身控制的累积误差等方面的因素导致与理论计算得到的轨道方程有一定的偏差,为了更好地模拟实际飞行情况,引入随机误差变量Ri,得到实际导弹的轨道方程为

其中,Rx、Ry、Rz为由于随机误差引起的轨道偏差,且轨道偏差为时间t的函数。在某一个时刻t0,轨道偏差服从正态分布,即

在任意时刻,且三个方向上的轨道偏差Rx、Ry、Rz均为0的时候,导弹实际的轨道方程会退化为导弹理论的轨道方程。

1.3 弹间最小距离计算方法

设两条空间飞行弹道表达式[12-14]

[x1(t1)-x2(t2)]2+[y1(t1)-y2(t2)]2+

[z1(t1)-z2(t2)]2

分别求导

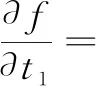
y′1(t1)+2[z1(t1)-z2(t2)]·z′1(t1)

要求解目标函数的极小值,则需要满足:

[x1(t1)-x2(t2)]·x′1(t1)+[y1(t1)-y2(t2)]·

y′1(t1)+[z1(t1)-z2(t2)]·z′1(t1)=0

[x1(t1)-x2(t2)]·x′2(t2)-[y1(t1)-y2(t2)]·

y′2(t2)+[z1(t1)-z2(t2)]·z′2(t2)=0

则飞行弹道间最小距离求解转换为非线性方程组的求解问题,求解即可得到导弹飞行弹道表征的异面曲线之间的最小距离。

1.4 弹道交叉碰撞概率计算方法

通过对大量导弹飞行的理论与精确弹道数据间的误差进行统计,分析导弹飞行位置误差分布,进而得到导弹飞行的位置误差和状态矢量的协方差矩阵,并将上述协方差矩阵转换至同一坐标系中,可以得出弹间碰撞概率为三维高斯密度分布概率函数在总包络球中的积分。然后,对三维高斯密度分布函数在相对速度方向进行数值积分,将碰撞概率的计算公式简化成二维高斯密度分布概率函数,并求解其在总包络球投影圆域中的积分。

假设已知两枚导弹在各自发射坐标系中的位置误差协方差矩阵分别记为CS与CR。根据在地心坐标系中两枚导弹位置矢量和速度矢量,进行坐标换算,可以求解发射坐标系到地心坐标系的转置矩阵。这里将由发射坐标系到地心坐标系的转置矩阵表示为P,由地心坐标系到发射坐标系的转置矩阵表示为Q,如下式所示。

CS1=PCsP-1
CRl=QCRQ-1

两导弹在速度坐标系中位置误差协方差矩阵均是对角矩阵。

上述两协方差矩阵是不相关的,相加即可得到相对位置误差的协方差矩阵。

Cc=CS1+CR1

相对位置矢量和相对速度矢量的表达式为:

Xc=rS-rR
Vc=vs-vR

定义地心坐标系到相遇坐标系的转换矩阵为U,在相遇坐标系中,相对位置矢量与协方差矩阵的转换公式如下所示[8,11-12]。

X=UXe
C=UCeU-1

在完成相关系数的转换后,即可用三维高斯分布概率函数来表示两个相遇物体间的不确定性关系。

式中,|C|是协方差矩阵的行列式的值。

将上述方程沿着其相对运动方向进行数值积分,即可消掉与速度平行方向上的一维,完成三维概率分布函数向二维的简化。

已知相遇坐标系中,导弹的位置矢量为

概率函数密度的表达式为

随后我们对z方向积分,将三维积分化为二维;此时将x,y看作已知量,对后半部分做进一步简化,令

将z分离,配方得到

直接对函数f(x,y)在投影区域内进行数值积分,即可求出弹道交叉碰撞概率,如下式所示。

P=∬f(x,y)dxdy

由于式中含有交叉项,为简化计算,进行坐标旋转可得

其中，

此时,经坐标系旋转后得到的坐标系表示为O-XY,其圆心O位于导弹的质心,X轴与Y轴分别对应于坐标系旋转之前相遇平面坐标系的X轴与Y轴。积分区域则为总包络球投影区域经过坐标旋转后的区域。

所以其碰撞概率计算公式为

对O-XY进行坐标平移,让积分区域中心移动到坐标系原点,则碰撞概率求解公式可表示为

2 碰撞概率计算流程

碰撞概率计算流程如图2所示。

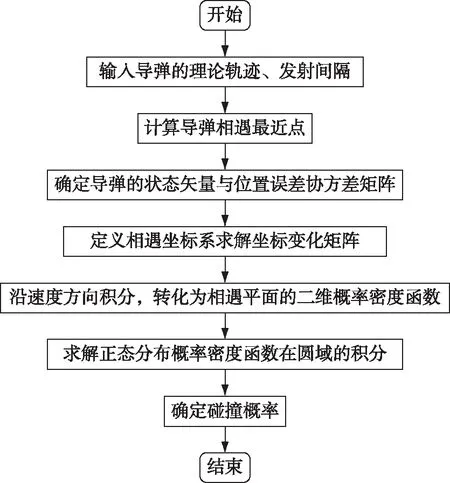
图2 碰撞概率计算流程

3 结束语

本文针对弹道导弹弹道交叉碰撞问题,建立了空间概率分布模型,推导求解了弹道导弹在三维空间中的空间碰撞概率,为确定弹道导弹集群发射时最小时间确定提供了计算方法,为发射阵地和发射时序的最优化确定提供了决策依据。