基于SHEPWM与谐波补偿技术的混合逆变策略

张兵锋，刘 洁，汪时交，闫 亮，周弘哲

（92925部队，山西长治046000）

电力系统的谐波问题早在20世纪20年代就引起了人们的注意，谐波研究具有重要的意义。谐波不仅对电力系统危害严重，对通信设备及电子设备会产生严重干扰[1-2]。谐波污染已经成为阻碍电力电子技术应用的主要障碍之一，由此产生了多种消除谐波的策略，如PWM技术、多电平技术及多重叠加技术等[3-5]。

设计了一种新型谐波补偿器，由1 个圆形变压器和2 个三相逆变器组成，具有输出可调、功率小、体积小、重量轻的特点。将谐波补偿器生成的谐波注入逆变系统可以消除特定谐波，且不影响逆变系统的功率及开关频率，可应用于大功率逆变场合。

为充分拓展谐波补偿器的应用价值，利用SHEPWM 技术可应用于大功率场合的优点，提出将SHEPWM 技术与谐波补偿技术混合应用于逆变系统[6-7]。谐波补偿器用来抑制主逆变电路输出中的5、7 次谐波，谐波补偿器的功率为5、7次谐波功率之和，相较于主逆变电路功率很小。采用SHEPWM 技术时，随开关角数目的增加，非线性超越方程组的求解将非常困难。目前，学者们已经提出了许多优化算法，但当开关角数目增大到5以上时，计算量大，部分区段求解收敛困难，不适合实时控制。这里，主逆变电路采用SHEPWM 技术消除11、13 次谐波，只需要计算3 个开关角，比较容易实现。

与传统的多重叠加逆变装置比较，此逆变系统可大大降低装置质量和体积，且此逆变系统消除影响较大的低次谐波极为有效[8]，若在负载电路中加入滤波环节，谐波的抑制效果会更好。

1 逆变系统设计

1.1 多相绕组圆形变压器

其基本结构与感应电机类似。圆形变压器铁芯包括原边和副边2 部分。为解决应力问题，副边铁芯固定不动[9]。

多相绕组圆形变压器的绕组结构见图1。原边为a1b1c1绕组与a2b2c2绕组，副边为三相绕组ABC。绕组a2b2c2在空间上从绕组a1b1c1逆时针偏转150°。绕组a1b1c1和绕组a2b2c2分别由1组三相桥式逆变电路供电。

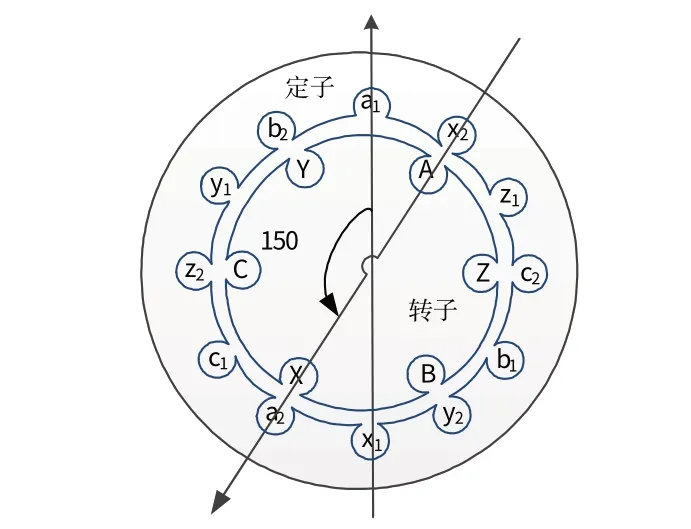
图1 圆形变压器Fig.1 Round transformer

1.2 逆变系统电路结构

混合逆变系统的电路设计如图2 所示，主逆变电路为1 个三相桥式逆变器，采用SHEPWM 技术控制。谐波补偿器由2个三相逆变器来供电。

在六相感应电机中，通过时间、空间的相位关系选取，可消除定子磁动势中的5、7次谐波。同时，加强基波磁动势，消除6次基频的脉动转矩。这里，将用该装置获得相反结果，即消除定子磁动势中的基波磁动势，加强并获得5、7次谐波。通过对时间、空间相位关系的控制，谐波补偿器在圆形变压器内部应用电磁感应原理对主逆变电路输出中的5、7谐波进行消除[10]。

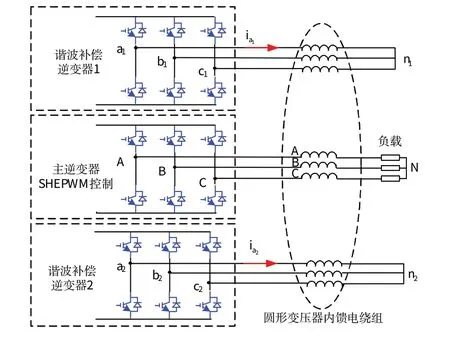
图2 逆变系统电路结构Fig.2 Circuit structure of inverter system

1.3 逆变系统数学模型

2 SHEPWM技术原理与应用

在电力电子领域，大功率的电能变化占据着重要的地位，可用于大功率应用场合的逆变技术显得尤为重要。在众多PWM调制技术中，SHEPWM技术是少有的可应用于大功率场合的逆变技术[11-15]。

2.1 SHEPWM原理

特定谐波消除PWM 技术的关键是开关角的求解，消除n个特定谐波需要计算n+1 个开关角的值。图3 以单相桥式逆变器为例，给出消除2 个特定谐波的一种脉冲形式。开关管除了在0、π、2π 处切换之外，还要在α1、α2、…、2π-α2、2π-α1等相位点处切换，α1、α2、α3即需要计算的开关角。

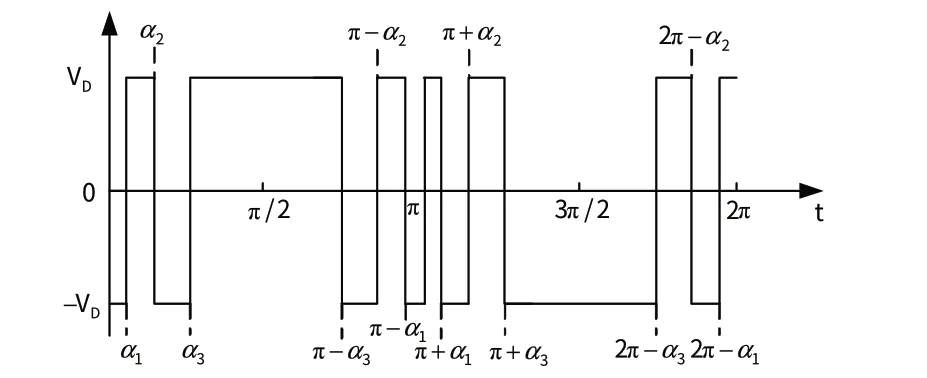
图3 特定谐波消除脉冲方式Fig.3 Specific harmonic elimination pulse mode

图3 波形不仅奇对称，而且关于1/4 周期波对称。此波形可以用傅里叶级数来表示，且其中既不含余弦项，又不含偶次谐波。其傅里叶级数表达式为：

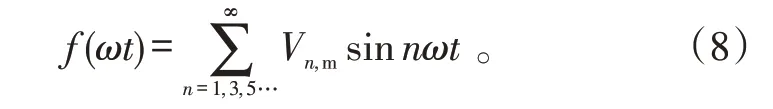
当目标为消除11、13 次谐波时，根据式（8），基波以及11、13次谐波应该满足：

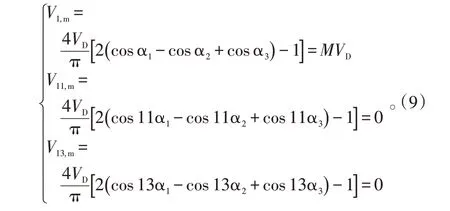
将开关角给定为0、π/3、π/2 时，不同调制比系数M对应开关角的曲线如图4 所示，对应消除11、13 次谐波后5、7次谐波相对幅值如图5所示。

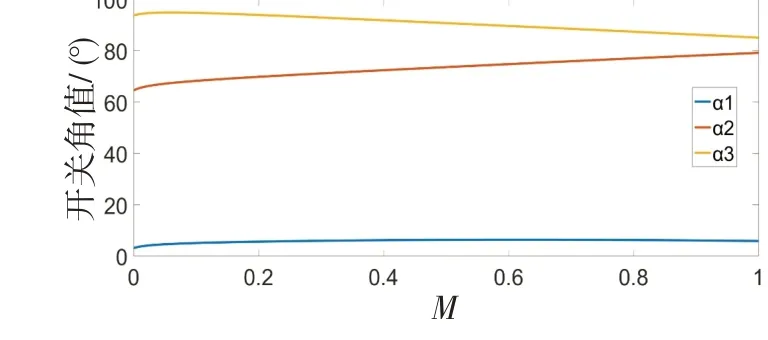
图4 开关角曲线图Fig.4 Switching angle curve

图5 谐波相对幅值曲线图Fig.5 Harmonic relative amplitude curve

2.2 SHEPWM技术应用

当逆变系统中主逆变器应用SHEPWM 技术，谐波补偿器不参与工作时，Simulink 仿真模型如图6 所示。

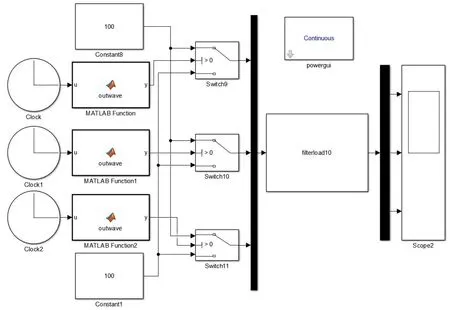
图6 主逆变系统仿真模型Fig.6 Simulation model of main inverter system

运行仿真得到的负载电阻两端电压波形如图7 a）所示。对A 相负载两端电压波形进行频谱分析结果如图7 b）所示。从频谱分析结果可以看出，11、13 次谐波基本被消除，5、7 次谐波幅值很高，17、19 次谐波幅值相对较高。

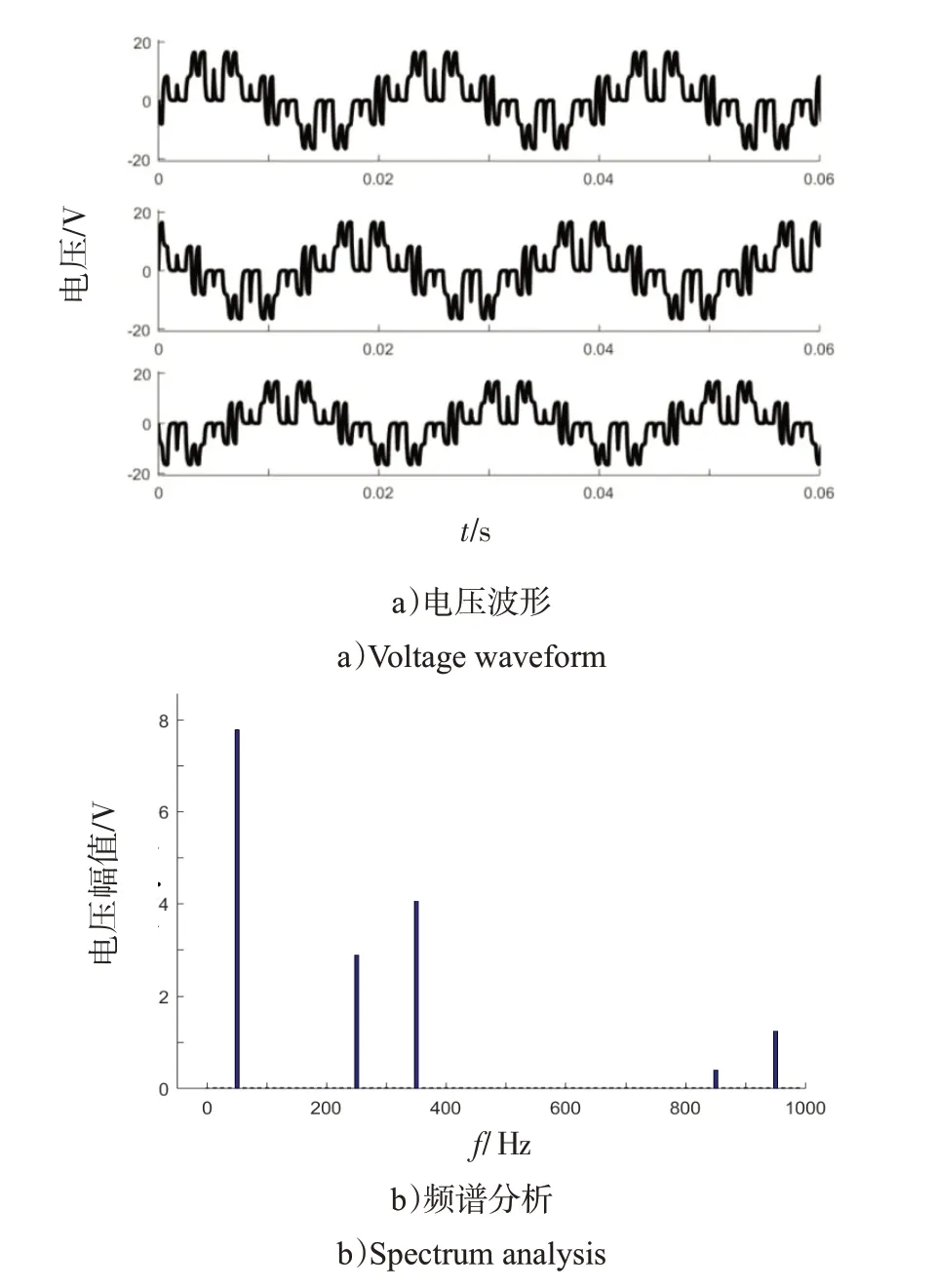
图7 电压波形及频谱分析Fig.7 Voltage waveform and spectrum analysis

3 混合逆变系统仿真

混合逆变系统中，主逆变器应用SHEPWM技术，以消除11、13 次谐波为目的。谐波补偿器参与工作时，Simulink 仿真模型如图8 所示。运行仿真可以得到负载电阻两端的电压波形如图9 a）所示。

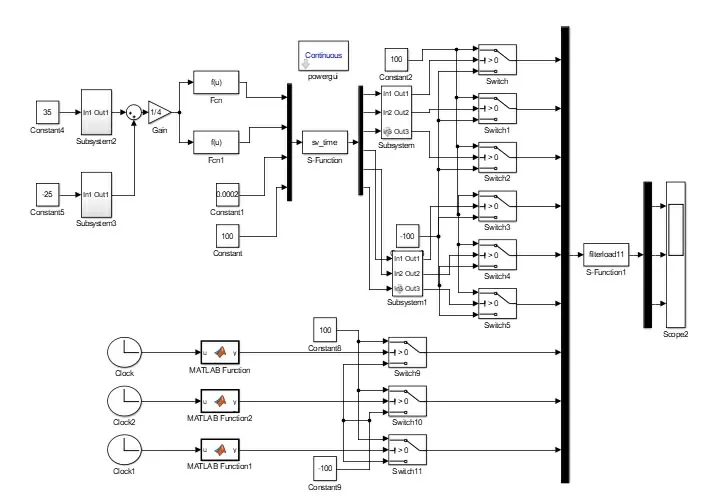
图8 逆变系统仿真模型Fig8 Simulation model of inverter system

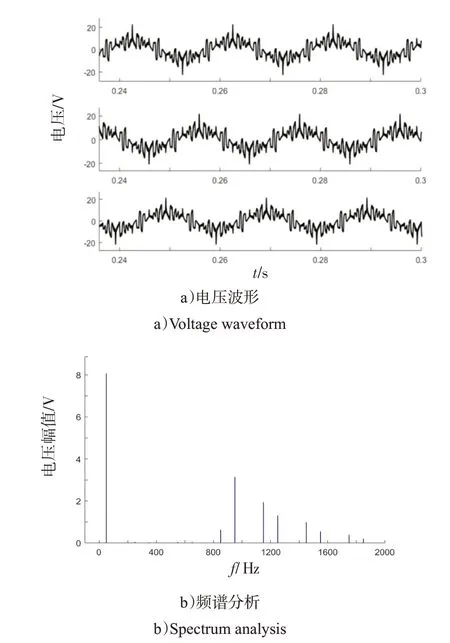
图9 电压波形及频谱分析Fig.9 Voltage waveform and spectrum analysis

将频谱分析的最高频率设置为2 000，对A 相负载两端的电压波形进行频谱分析结果如图9 b）。从频谱分析结果可以看出，5、7、11、13 次谐波幅值基本被消除，17、19 次等高次谐波仍然很多。仿真分析结果表明，SHEPWM 技术与谐波补偿技术的混合逆变起到了作用，成功消除了5、7、11、13 次谐波。但SHEPWM 调制引起了谐波的分布向高频漂移，所以17、19次等高次谐波仍然较多。

改变负载阻值进行仿真。仿真结果与A 相的结果基本一致，但随着负载电阻阻值的增加，输出波形质量变差。这是由于圆形变压器的绕组线圈起到了一定的滤波作用，随着电阻阻值的增加，绕组线圈的滤波作用越来越小，故输出波形逐渐变差。此时，想要输出质量更高的波形，就需在负载电路中加入滤波环节。

当逆变系统中主逆变器仍然采用SHEPWM技术控制，谐波补偿器参与工作，将负载改为阻感负载。运行仿真可得到负载电阻两端的电压波形如图10 a）所示。将频谱分析的最高频率设置为2 000，A 相负载电阻两端的电压波形频谱分析结果如图10 b）。从电压波形图可以看出，负载电阻两端电压波形已经很接近正弦波，波形质量较高。从频谱分析结果可以看出，5、7、11、13次谐波幅值很低，基本被消除，17、19次等高次谐波幅值也很低。

图10 电压波形及频谱分析Fig.10 Voltage waveform and spectrum analysis

仿真分析结果表明，由于混合逆变的作用，主要的低次谐波被消除，剩余的谐波能量主要分布在高次谐波，便于滤波。当负载电路中加入滤波电感后，滤波作用明显，获得较高质量的输出电压波形。

4 结论

基于SHEPWM技术及谐波补偿技术的混合逆变系统充分发挥了谐波补偿器的价值，利用SHEPWM技术能够应用于大功率场合的优点，能够减小逆变装置体积与重量，同时抑制逆变系统的低次谐波。

以消除11、13 次谐波为例，介绍了指定谐波消除脉宽调制技术的原理，仿真验证了SHEPWM 技术消除指定谐波的有效性。

将SHEPWM技术与谐波补偿技术混合起来应用于逆变系统进行仿真实验，结果证实了混合逆变系统消除特定低次谐波的有效性。尤其是，加入滤波电路后效果更好。混合逆变的实现为逆变技术以及谐波治理技术提供了新的思路与方向。