带p-Laplacian算子四阶边值问题多重正解的存在性

钟文颖，宋常修

（广东工业大学应用数学学院，广东广州510520）

关于对带p-Laplacian算子的微分方程的研究在学术界已经是一个经典的话题，且已取得显著成果［1-6］。因为这些方程在诸多领域有广泛应用，如流体动力学、空气动力学、量子力学、电子学和天体物理学等科学领域，从而吸引了众多学者的关注。如文献［7］借助度理论，得到了二阶p-Laplacian边值问题解的存在性，更有文献［8］利用不动点指数，得到了如下奇异边值问题的多重正解存在的充分条件

然而，关于四阶的p-laplacian算子边值问题的研究仍未完善。因此，为了推广和完善文献［8-10］的主要结果，本文将运用Leggett-Williams不动点定理，考虑如下四阶Sturm-Liouville边值问题

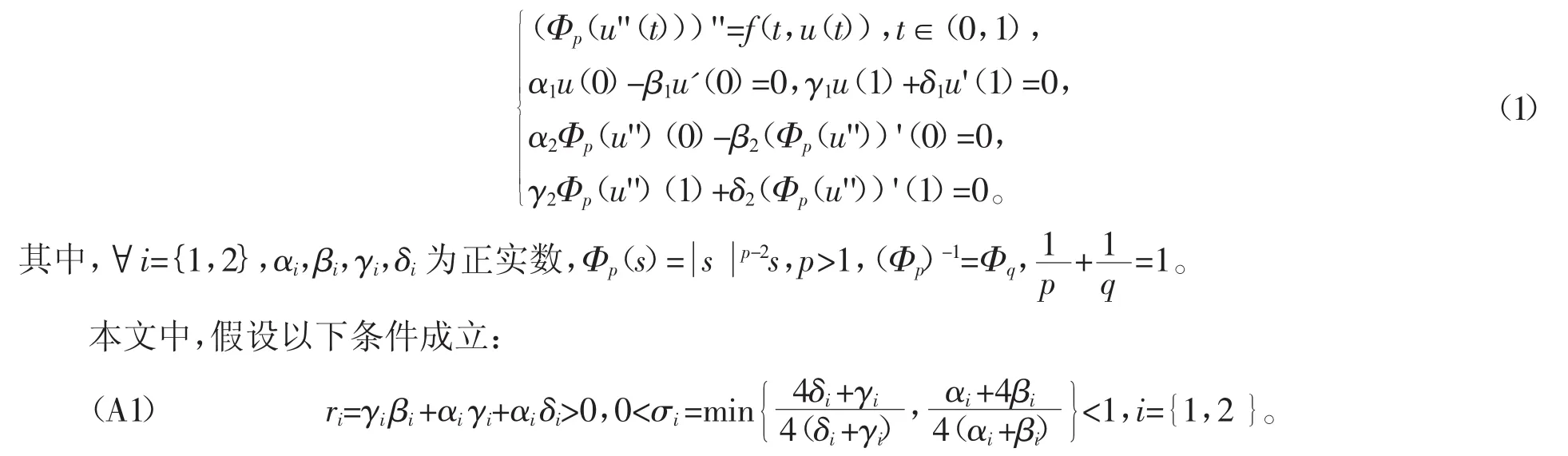
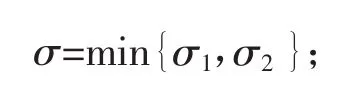
（A2）Hi（t，s），i=｛1，2｝为关于微分方程u''（t）=0，t∈（0，1）及满足如下边值条件αiu（0）-βiu'（0）=0，γiu（1）+δiu'（1）=0的格林函数，即

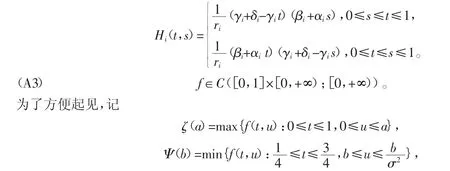
其中σ由（A1）给出。

1 预备知识

2 主要结果及证明