等宽明渠交汇口壅水特性数值模拟
2020-07-25王玲玲丁少伟
周 舟,曾 诚,周 婕,王玲玲,丁少伟
(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;2.河海大学水利水电学院,江苏 南京 210098; 3.河海大学力学与材料学院,江苏 南京 210098)
明渠水流交汇现象广泛存在于灌溉和引排水工程中。在明渠交汇口处,水流结构复杂、水力特性独特。明渠交汇口水力特性研究对城市内涝治理、河口冲淤预测、污染物输移控制等诸多工程领域都具有重要意义。国内外学者针对明渠交汇流进行了大量研究。Taylor[1]对渠道水流交汇现象进行了理论分析与试验研究,认为上下游水面线的变化与支干流流量比、交汇角等因素有关。Ramamurthy[2]通过假定交汇明渠的上下游水深比,初步建立了能够描述水流交汇区域水力特征的理论模型。Hager[3]基于水槽模型试验观测,对交汇水流上下游水深比与众多水力要素的关系进行探讨并得出结论:流量比与交汇角是影响上游壅水高度的主要因素。Hsu等[4]通过物理试验研究,得到正交工况下上游水位壅高值与流量比之间的关系。茅泽育等[5]通过对交汇区域上下游水深影响要素的假设,得到水深比与流量比、弗劳德数、交汇角度等水流要素之间的理论关系,在后续的数值研究[6-7]中,研究者从能量、动量输运等角度详细分析了水面线变化与水流结构之间的关系。王晓刚等[8]针对Y型汇流口建立一维数学模型,探究流量、交汇角等影响因素对汇流口水深的影响规律。刘同宦等[9]通过90°水槽物理试验,研究分析不同流量比下时均流速分布与交汇口下游水面线变动之间的关系。Zeng等[10]通过构建RANS-LES混合模型,提出能够准确捕捉明渠交汇区域自由液面的数值方法。Yuan等[11]对正交明渠水流的水动力场进行详细的物理测量,得到流速、应力、紊动能等水力要素的数据及其分布情况。
本文采用RSM模型封闭控制方程,利用体积函数法(VOF)追踪自由表面,建立三维数值模型,对等宽明渠交汇口的壅水问题进行数值模拟研究。通过对不同交汇角和流量比工况的计算,分析交汇角和流量比对交汇口附近水面变化的影响,探究交汇角和流量比与交汇口上下游水深比之间的关系,为渠道工程设计与实践提供参考。
1 数 值 模 型
1.1 控制方程
计算区域内水流运动满足动量方程和质量守恒方程:
动量方程
(1)
质量守恒方程
(2)

1.2 雷诺应力模型
雷诺应力模型(RSM)通过直接求解雷诺应力输运方程计算雷诺应力。相比于涡黏模型,摆脱了各向同性涡黏性假设的限制,能够反映更多的湍流物理机理,因而在工程领域具有其他紊流模型不可比拟的优势。
Reynolds应力输运方程:
(3)

式中:ν——流体动力黏度。其余符号含义见文献[6]。
1.3 体积函数法
采用VOF对自由液面进行模拟。在网格单元中,设定水的体积为Vw,网格单元的体积为Vc,水的体积分数aw满足:
(4)
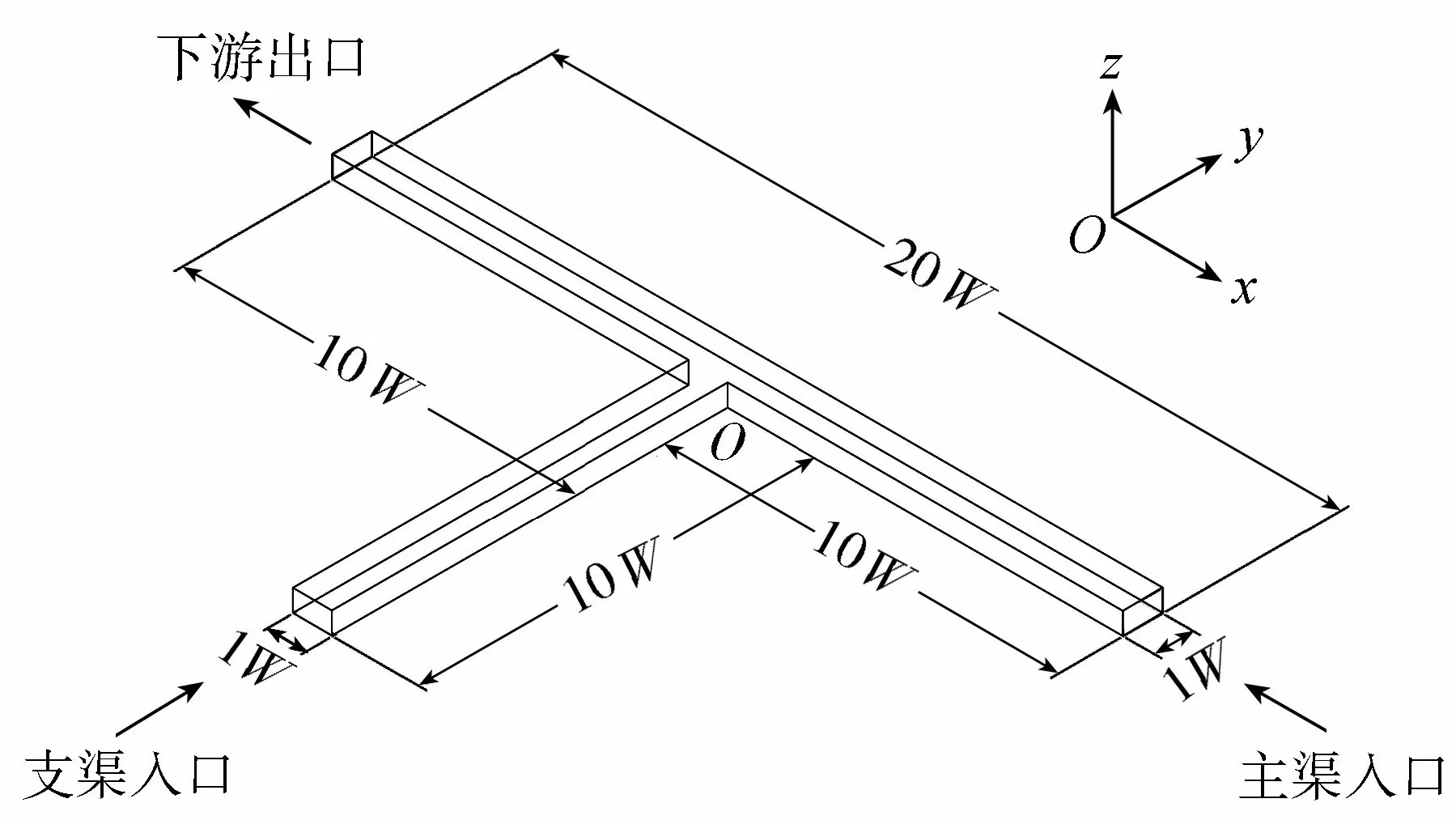
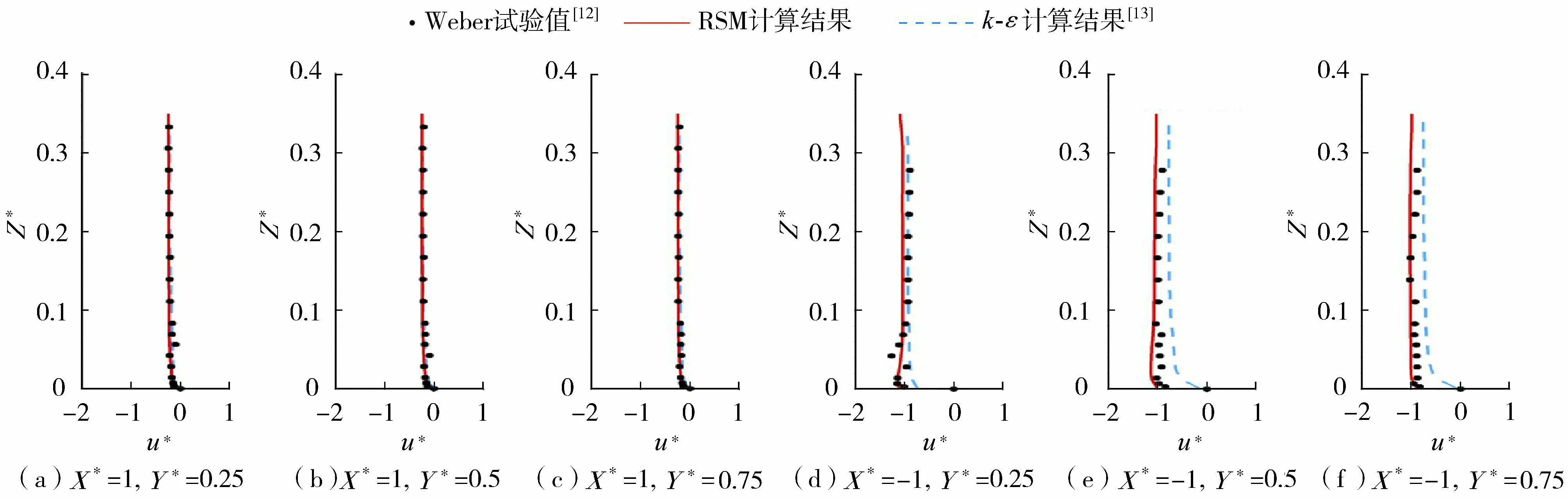
aw=1,表示网格单元内全部为水;aw=0,表示网格内全为空气;0 (5) 通过对aw迭代求解,可根据式(6)进一步确定网格单元内其他的特性参数。 φ=awφw+(1-aw)φa (6) 式中:φ——网格内其他参数,如密度、分子黏性系数等(下标w表示水,a表示空气)。 采用有限体积法对控制方程进行离散,速度与压力解耦采用PISO算法,其他项离散均采用QUICK格式。计算边界如图1所示,主渠与支渠入口均为速度进口,流速方向垂直于进口断面;下游出口为压力出口,尾水位高度与实测值一致,出口压力满足静水压强分布,液面相对压强为0;壁面边界忽略粗糙度影响,采用无滑移标准壁面函数法对近壁区流动进行模拟。 图1 计算区域示意图(θ=90°工况)Fig.1 Schematic of the calculation area (θ=90°) 本文研究对象为矩形断面的等宽明渠交汇口,交汇角度θ变化范围为30°~90°。参考Weber等[12]的物理模型,选取渠宽W=0.914 m,渠道高度为0.509 m。为使主渠和支渠内水流到达汇流区时充分发展,选取主渠长度为18.28 m(20W),支渠长度为9.14 m(10W)。支渠距离主渠入口9.14 m(10W)。图1所示为交汇角θ=90°工况的计算区域,x、y、z轴正方向如图所示,坐标原点位于支渠入口上游侧渠底。 采用六面体和四面体网格对计算区域进行剖分。x、y、z方向均采用非均匀网格,x、y方向上对交汇区域和近壁区域进行加密,z方向上对液相域和近壁区域进行加密。对于本文所涉及的7种交汇角工况(30°、45°、60°、65°、75°、85°和90°),经网格无关性验证,确定网格数在31万(90°工况)~ 36万(30°工况)之间。 选取90°等宽明渠交汇水流试验的实测数据[12]对模型进行率定。验证工况中,主渠上游流量Qu= 0.042 m3/s,支渠上游流量Qb= 0.127 m3/s,流量比q=Qu/(Qu+Qb) = 0.25,其中下游出口流量Qd=Qu+Qb,下游水位为0.31 m。图2为交汇区附近沿程水面线计算结果,图3为交汇区下游各测点的流速剖面,图中将此次RSM计算结果与实测数据和文献[13]中的k-ε模型计算结果进行了比较。对图2中的坐标变量无量纲化(X*=x/W,Y*=y/W,Z*=z/W),u*=u/Ud,v*=v/Ud,w*=w/Ud,Ud为尾水断面平均流速。 由图2可见,在水面线结果对比方面,RSM计算结果对交汇区附近水位壅高与跌落特征捕捉准确;与k-ε模型计算结果相比,RSM不仅能够更准确地模拟上下游水位,并且在水位变化剧烈的区域也能精确地捕捉水位的迅速跌落和缓慢抬升。由图3可见,在速度剖面对比方面,RSM计算结果与实测值吻合较好,与k-ε模型计算结果大体一致,未体现出明显的模型优势。综上所述,就本次模型验证而言,与k-ε模型计算结果相比,RSM在水面线计算精度方面具有明显优势,在速度剖面计算精度方面没有明显改善。 图2 自由液面计算结果对比Fig.2 Comparison of free surface profiles 图3 交汇区下游测点流速剖面对比Fig.3 Comparison of streamwise velocity profiles 在对模型充分率定的基础上,对3种流量比(q=Qu/Qd= 0.25、0.417和0.75)和7种交汇角(θ= 30°、45°、60°、65°、75°、85°和90°)的21个组合工况进行计算。为比较不同流量比和交汇角对明渠交汇口的壅水影响,各工况的下游流量和下游水位均分别为0.17 m3/s和0.31 m。 为对计算结果进行分析,定义主渠上游水深hu、支渠上游水深hb和交汇口下游水深hd分别为断面AB、CD和EF处水深,3个断面距离坐标原点O的平面距离分别为2W、2W和8W,断面位置如图4所示。由图2可见,各特征水深在其相应断面位置已达到稳定。 图4 断面位置示意图Fig.4 Locations of selected sections 3.2.1 上游水深比分析 图5 上游水深比计算结果Fig.5 Results of upstream depth ratio 3.2.2 壅水形态分析 图6和图7分别为流量比q= 0.25时,不同交汇角(30°、45°、60°、90°)工况下的三维水位云图和沿程水面线分布。由图6可见,由于支流汇入的顶托作用,上游壅水区内形成明显的水位壅高,汇流区和集流区域内出现水面跌落现象。随着交汇角θ逐渐增大,支流入汇引入y方向的水流动量增大,对主渠上游来流的顶托作用增加,汇流区域和集流区域中水面跌落的范围增大,水面跌落现象更明显。由图7所示的沿程水面线分布可见,随着交汇角增大,上游水位逐渐增大,下游最小水深逐渐减小。其他流量比工况下,不同交汇角对明渠交汇口壅水形态的影响大体类似。 图6 不同交汇角工况下的三维水位云图Fig.6 3D water-level contours for different junction angles 图7 不同交汇角对自由液面的影响Fig.7 Impact of different junction angles on free surface 3.2.3 上下游水深比和最大水深比分析 (7) (8) 式中:hm——交汇口水面跌落区域内的最小水深。 图和计算结果Fig.8 Calculation results of 3.2.4 上下游水深比变化范围分析 图9 上下游水深比范围Fig.9 Variation range of the upstream-to-downstream depth ratios a. 通过与原型物理模型测量数据的比较,发现在明渠交汇口附近水面线计算精度方面,RSM的表现优于k-ε模型。 b. 主渠和支渠的上游水深近似相等,相对误差不超过2%。 c. 对明渠交汇口附近三维壅水形态进行分析,由于支流汇入的顶托作用,上游壅水区内形成明显的水位壅高,汇流区和集流区域内出现水面跌落现象。同一流量比工况下,随着交汇角的增大,上游水位逐渐增大,下游最小水深逐渐减小。 d. 计算得到所有工况的上下游最小水深比和最大水深比。在本文研究的流量比及交汇角变化范围内,上下游最小水深比和最大水深比均随交汇角的增大而增大,随着流量比的增加而减小。 e. 对上下游水深比的变动范围进行分析。同一流量比工况下,随着交汇角的增大,上下游水深比的变化范围明显增大,交汇口附近水面变幅增大;同一交汇角度工况下,随着流量比的增大,上下游水深比的变化范围明显减小,交汇口附近水面变幅减小。
1.4 数值方法及边界条件
1.5 计算区域
2 模 型 验 证

3 等宽明渠交汇口壅水特性分析
3.1 数值模拟工况
3.2 结果分析和讨论





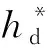
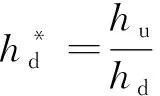



4 结 论
