深槽护底带对水位的影响*
2020-07-25朱玉德李少希刘鹏飞
朱玉德,李少希,刘鹏飞
(交通运输部天津水运工程科学研究所,工程泥沙交通行业重点实验室,天津 300456)
三峡水库蓄水后,上游来沙大量减少,导致坝下砂卵石河段河床滩槽不均匀冲刷下切。随着河床冲刷的发展,沿程水位逐渐下降,河床冲刷与水位下降不同步的变化给航道带来了两方面问题:一是枯水位的下降导致船闸下引航道水深难以维持设计尺度;二是局部深泓高凸的卵石浅滩段航道条件因为水位降落而持续恶化。解决问题的关键在于抑制冲刷进而控制水位的下降。在护岸、护滩工程维持河段边界稳定的基础上,为了抑制冲刷、稳定航道水位,相关部门还实施了修建潜坝、护底带等措施。总体而言,护底带较潜坝的壅水效果更优,且由此带来的局部流速、比降增大现象相对较小[1]。但护底带通常修筑于抗冲能力强、横竖向变动小的深水区,水流条件复杂,参数确定较为困难。本文通过七星台深槽部位不同护底条件下的水位影响研究,为相关护底带布置提供参考。
1 河段概况
长江中游枝江—江口河段处于三峡工程下游沙卵石河段末端,上游紧邻芦家河重点浅滩河段,下游为抗冲性较弱的沙质河床,是长江中游最早受到三峡水库蓄水影响的沙卵石河段之一[2]。由于三峡清水冲刷影响,坝下河段水位出现较大幅度下降,据统计,2014年度在三峡下泄流量5 600 m3/s条件下,宜昌水位仅39.17 m,低于控制目标39.19 m。同时由于枝江—江口河段河床质差异,沿程冲刷不均匀、水位沿程降幅存在差异,枝江以上水位降幅较小,枝江—七星台水位降幅沿程逐渐增大,下游七星台—大埠街比降基本保持不变,曹家河—七星台段比降增加,5 300 m3/s流量下曹家河—七星台段2008、2010年比降分别增至1.1、1.4;加之三峡蓄水后柳条洲滩体面积急剧萎缩、滩体下移,滩形变狭长,吴家渡边滩冲刷,柳条洲—吴家渡边滩过渡段水浅、流急,航道条件恶化[3]。下游曹家河—七星台一带已成为控制上游水位下降的节点,若该处节点不控制,水位下降变化持续发展,将无法实现本河段规划航道尺度。为了抑制该区域河床持续冲刷、维持枝江以上河段水位的稳定,减少枝江以下水位的降幅,避免河床持续冲刷形成集中落差,荆江河段航道整治工程中,在七星台深槽部位实施3道护底带工程(图1)。

图1 七星台护底带平面布置
2 模型设计
2.1 模型设计及率定
1)为准确分析不同护底条件对水位变化的敏感性,模型采用几何比尺较小的正态模型。研究河段河宽约1 500 m。选择比尺为100的全河宽正态模型试验场地,供水等条件较为困难,因此,采用大区域半江模型以克服模型建立中场地、供水等的限制。但选取的模型研究宽度须远大于工程引起的流速变化区域,并确保选取区域内水流大小和方向的相似。据数学模型计算,工程后右侧护底头部流速受工程影响区域不大于120 m,由此确定模型范围横向左侧至七星台深槽左岸、右侧至吴家渡边滩滩脊处,共0.7 km宽区域;纵向上至董家湾、下至阮家湾区域[4-6]。模型满足如下相似关系:
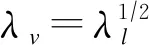
(1)
(2)

(3)
式中:λl为水平比尺;λh为垂直比尺;λv为流速比尺;λQ为流量比尺;λn为阻力比尺。
2)模型为半江模型,左侧按天然河岸地形控制水流流向;右侧为一个流切面,根据数学模型计算流线方向、设置动边界以控制各流量下模型流速方向,模型地形按实际地形模拟。试验前据数学模型计算的模型进口流量、断面流速分布、水位及边界条件对模型进行率定,率定流量分别为5 300、8 750、12 500、35 000 m3/s;通过进口及边缘活动边界调整模型水流大小及流向,使局部正态模型与数学模型提供的水位、流速等能够相似,满足试验要求。
2.2 试验水文条件、试验方案
依托七星台深槽护底初步方案开展护底带水位影响多组试验研究,见表1。试验选择对河段最常出现、较不利的水动力条件,包括:三峡蓄水后常出现的洪水流量35 000 m3/s、三峡蓄水后多年平均流量12 500 m3/s、整治流量8 750 m3/s、设计流量5 300 m3/s。

表1 试验方案
3 试验结果分析
3.1 护底带不同间距对水位影响
不同流量下护底带间距变化与水位关系见图2,分析可知:
1)流量、压载厚度一定,护底带壅水效果随间距增加而增加,当护底带间距达到某一距离时,护底带上游水位壅高达到最大;若护底带间距进一步增加,其壅水效果开始减弱。流量5 300 m3/s、压载2 m条件下,当护底间距100 m时,工程上游最大壅水7.0 cm,约300 m时工程上游最大壅水8.2 cm,间距500 m时上游最大壅水6.1 cm。
2)压载厚度一定、护底带阻水面积不变条件下,随着流量增加,护底带壅水效果最佳时的护底间距也逐渐增大;当来水超过某一流量级时,护底带壅水效果逐渐减弱,护底带间距的调整对壅水的作用已不明显。
3)压载厚度一定,护底上游的壅水高度随着流量的增大而减小。小流量时护底带淹没深度小,对纵向水面线的影响要大;大流量时护底带淹没深度大,对纵向水面线的影响略小。

图2 护底带间距与水位关系
3.2 护底带不同压载厚度对水位的影响
与平整床面相比,护底带人为造成了河床床面凸起,使得相同流量与相同出口水位的水面线抬高,工程区发生壅水;水流越过工程区后,过水断面扩大,水位跌落,距离最后一条护底带下游约200 m左右水位降至最低,之后逐渐恢复。流量相同、护底间距一定的条件下,护底是否压载及压载厚度对工程区水位产生明显影响,压载体厚的护底带沿程水面线变化幅度要明显大于压载体薄的护底,同一流量不同压载厚度下护底带对纵向水面线影响趋势基本相似,但压载较厚的护底更容易导致深槽航道流态趋差,对航行安全带来影响。由图3可知,5 300 m3/s流量下,压载厚度为3 m时,工程区域最大壅水高度达10 cm;压载厚度为2 m时,工程区域最大壅水高度为8 cm。

图3 流量5 300 m3/s护底不同压载厚度下工程区域水面线变化
3.3 护底带最佳间距
护底带不同间距、不同压载厚度的试验表明:护底带对上游水位的影响与护底带间距、护底带阻水面积、来流量等有关;同一流量情况下,随护底带压载厚度的增加,护底带壅水效果最佳间距也逐渐增大。图4表明:七星台深槽护底在压载厚度为2 m、设计流量下(5 300 m3/s)护底带平面间距应优化至300~340 m较为合理。

图4 流量5 300 m3/m下护底带间距、高度变化与水位关系

(4)
式中:L为最佳护间距;v0为建前流速。
通过式(4)计算得到:江口七星台深槽护底带设计护底带压载厚度2 m条件下最优间距为325 m。
4 护底带对水位下降溯源传递的影响
护底带对下游水位降落敏感性研究以护底带排上抛石压载2 m、间距为325 m方案为基础,模拟下游水位降落0.3、0.5、1、1.5 m条件下有、无护底带沿程水位变化情况,见图5。研究表明:
1)相同流量、无护底条件下,若下游水位降落,则七星台深槽沿程水位普遍降落,且沿程降落幅度基本一致;护底工程实施后若下游水位降落相同值,则工程区及上游沿程水位降落幅度明显减小。5 300 m3/s流量、下游水位分别降落0.3、0.5、1.0、1.5 m时,无护底条件下试验段上边界水位分别降落0.29、0.48、0.95、1.45 m,而护底后试验段上边界水位分别降落0.252、0.427、0.889、1.377 m;12 500 m3/s流量、下游水位降落条件下,有、无护底时沿程水位变化趋势与5 300 m3/s流量下基本一致。据此可知,护底带对下游水位降低向上游传递具有明显减弱效果。
2)相同流量不同出口水位条件下,同一床面凸起高度抬升水位的幅度不同。出口控制水位越低、水深越小,水位抬升幅度越大,且水位抬升幅度随出口控制水位的变化存在突变。不同流量条件下,相同出口水位时床面凸起使得水位抬升的幅度不同,流量越大,则抬升幅度越大,且不同流量下水位抬升幅度随出口控制水位的变化转折点也不同。由上述分析可知,护底带工程的影响,产生了形态阻力,从而增大糙率,引起水面线的变化。
3)河床凸起也会影响到出口水位下降的溯源传递特性。同理可以分析,相同的流量和出口水位下,床面凸起较床面平整溯源传递的范围应该要小,且相同水位测站的水位降幅减小。换句话说,河床凸起本身将使上游水位受下游出口水位下降的影响程度变小,河床凸起抑制了下游侵蚀基准面降低的溯源传递,包括传递范围和幅度。
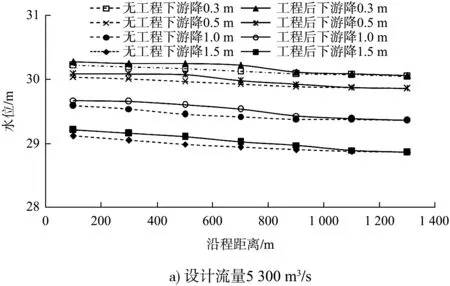
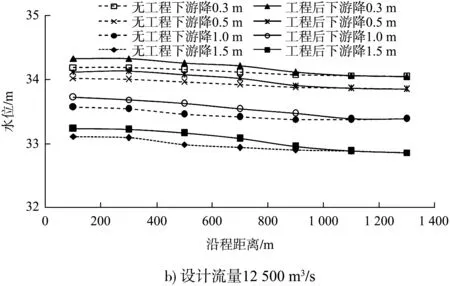
图5 下游水位不同降落幅度时工程区沿程水位变化
5 结论
1)采用局部正态模型,依托七星台深槽护底初步方案,通过研究护底带壅水效果与间距、高度的关系,提出了条形深水护底带壅水的影响规律。

3)护底带对水位下降溯源传递的影响研究表明:护底对下游水位降低向上游传递具有明显减
弱效果,原因是由于护底增加了河床形态阻力、河床糙率,从而引起水面线的不均匀变化,即人为的河床凸起改变了自然水位下降的溯源传递特性;另一方面护底能较好地抑制河床冲刷下切,两方面的综合作用使护底成为维持河段水位稳定、减少水位降幅、避免形成集中比降的有效措施。
