山区弯曲河道鱼类产卵栖息地适宜度的分布特征*
2020-07-25戴思遥廖尚超
钟 亮,戴思遥,廖尚超
(1.重庆交通大学 国家内河航道整治工程技术研究中心,重庆 400074;2.重庆交通大学 水利水运工程教育部重点实验室,重庆 400074)
天然河道大多数是弯曲的,由主流和二次流叠加形成的弯道水流结构复杂[1],尤其在山区河道弯曲段,其独特的河道形态和水流结构直接影响生物多样性[2],也为鱼类产卵栖息提供了较为理想的场所。鱼类生活栖息地包括产卵场、索饵场、越冬场以及连接不同生活阶段水域的洄游通道等(简称“三场一通道”)[3],其中产卵场是重要且敏感的鱼类栖息场所。开展山区弯曲河道鱼类产卵栖息地适宜度的分布特征研究,对河道鱼类资源保护和生态航道工程建设等具有重要意义。现有鱼类产卵生境指标体系方面的研究成果[4-5],为产卵栖息地适宜度问题研究提供了科学依据。目前,鱼类产卵栖息地适宜度问题的研究已取得一定进展:易雨君等[6]建立了四大家鱼产卵栖息地适宜度模型,讨论不同水文背景下的产卵场适宜度;王煜等[7]分析了大坝泄流方式与四大家鱼产卵栖息地适宜度的相关性;李永等[8]探讨了鱼类产卵生境面积随河道流量的变化特征;童朝锋等[9]、易亮等[10]、常留红等[11]研究了航道整治工程对鱼类栖息环境的影响。在弯曲河道鱼类栖息地适宜度研究方面,Krieger等[12]评估了鲟鱼产卵栖息地的质量,认为在弯道及流速变化较大区域其产卵栖息地适宜度较高;Macura等[13]建立了弯曲河道中鲑鱼的生境适宜度曲线,讨论鲑鱼生境适宜度与水深、流速间的响应关系;Parsapour等[14]、Harrison等[15]分析了山区河道形态变化对鱼类产卵栖息地适宜度的影响,探讨两者的相关性。总体而言,目前鱼类(四大家鱼)产卵栖息地适宜度问题研究仍不充分,针对山区弯曲河道的研究成果依然较少,弯曲河道中鱼类产卵栖息地适宜度的分布特征及其随流量的变化规律等问题还有待探讨。
本文以长江上游中盘子弯曲河段为例,以淡水养殖中重要经济鱼类四大家鱼为代表,基于平面二维水流数值模拟资料,探讨山区弯曲河道鱼类产卵栖息地适宜度指标随流量的变化特征,分析适宜度指标在弯道中的分布规律。研究成果将有助于丰富弯曲河道鱼类产卵栖息地适宜度分布问题的认识,并可为山区河道鱼类资源保护和生态航道工程建设等提供科学参考。
1 资料与方法
1.1 研究资料
中盘子河段位于长江上游,航道里程854~857 km,整个河势呈弯曲河道形态(图1),弯道中心角约69°,凸岸和凹岸的弯曲半径分别约为1.1 km和2.2 km。弯道进口为顺直段,在双线子附近右转形成急弯,凹岸有中盘子、对窝滩等石梁突伸江中,岸线抗冲能力强,限制横向冲刷发展,水流下切在礁石头部冲刷形成深槽;在弯道环流的作用下,表流冲向凹岸,泥沙则随底流输移至凸岸,在凸岸淤积形成狭长形分布的卵石边滩。中盘子河道两岸礁石密布,岸线极不规则,航槽弯窄,具有山区弯曲河道的典型特征。中盘子河段下游12.8 km有长江支流赤水河入汇,赤水河于贵州赤水市设有水文站,下游13.2 km有合江水位站,下游48 km有长江朱沱水文站(航道里程806 km),上述测站水文资料相对丰富,对研究河段的水文条件有较为完整的控制。
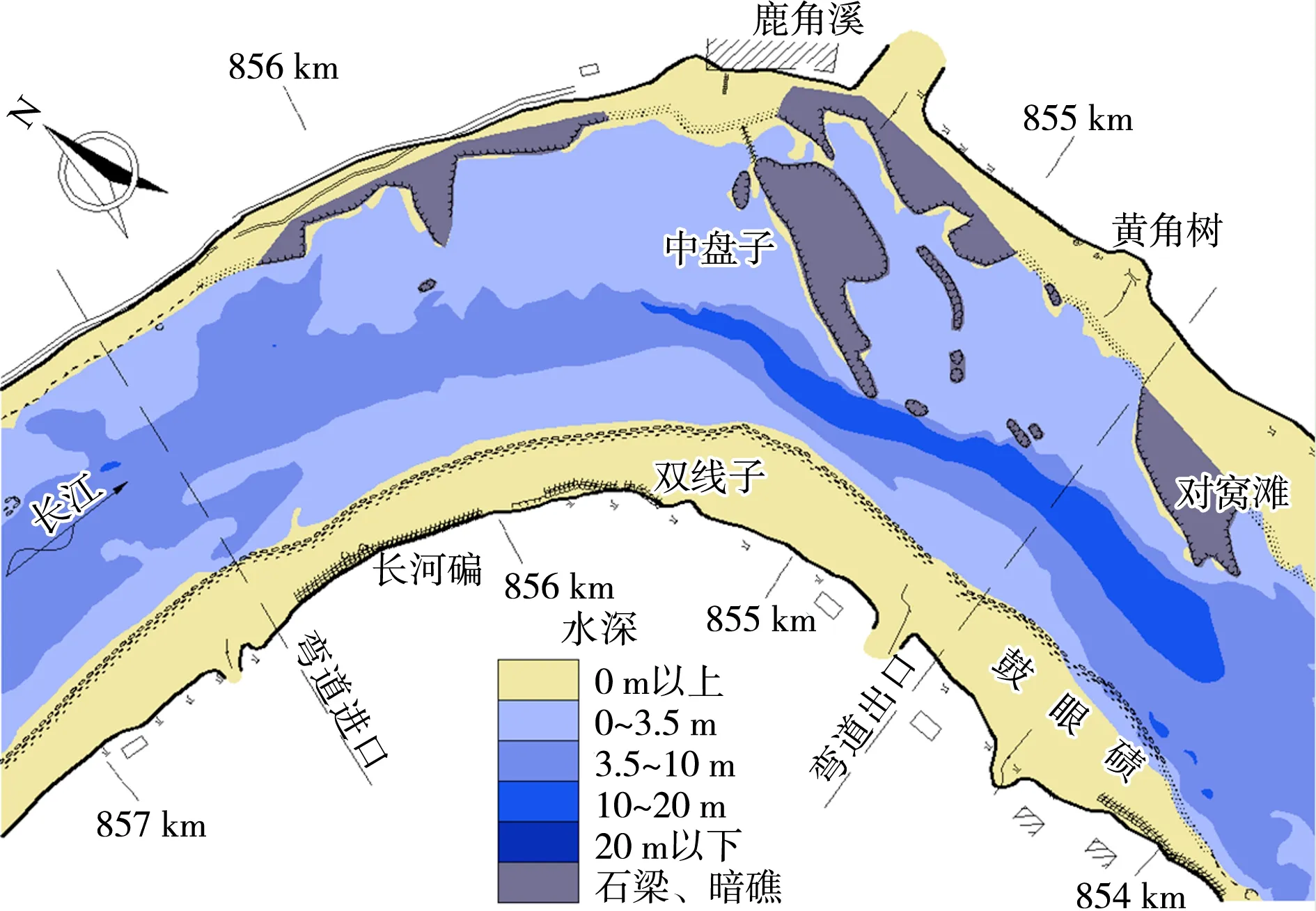
图1 中盘子河段河势
本文采用平面二维水流数学模型开展研究,模型的基本控制方程见式(1)~(3)。方程时间离散采用有限差分法,空间离散采用有限单元法,离散区域内采用6节点三角形等参单元,利用Newton-Raphson迭代法求解离散后的非线性代数方程。
水流连续方程:
(1)
x方向水流运动方程:
(2)
y方向水流运动方程:
(3)
式中:z为水位;t为时间;h为水深;u和v分别为沿x方向和y方向的流速;g为重力加速度;n为曼宁糙率系数;νt为涡流黏性系数,采用零方程模型确定,νt=(0.6±0.3)u*h,u*为摩阻流速,当遇急弯或断面急剧变化时νt取大值。当水流为恒定流时,各式中的时间导数项取为0。
河道水流数值模拟基于2015年3月实测的工程河段地形(测图比尺1:2 000,1985国家高程基准,1954北京坐标系),考虑弯道进出口顺直段的长度要求,取计算区域航道里程853~858 km,河段长约5 km,计算网格采用三角形非结构网格,共31 245个单元,63 000个节点,网格边长约15 m。进口流量采用朱沱水文站和赤水水文站实测流量的差值,出口水位综合考虑朱沱水文站和合江水位站水位,由一维水流数学模型推算得到。模型验证采用工程河段洪、中、枯多级流量下的实测水面线和流速流向资料,经率定得到工程河段各级流量下的综合糙率在0.031 3~0.034 7之间。模型验证结果[16]显示,计算和实测水面线的走势相同,水位偏差在±0.10 m以内;流速大小、分布以及最大值和最小值的位置均与实测资料吻合较好,流量偏差控制在±5%以内;数模计算的流场流向与浮标迹线走向较为一致。综上,本文建立的平面二维水流数学模型,计算精度满足JTS/T 231-4—2018《内河航道与港口水流泥沙模拟技术规程》的要求,可用于下一步研究。
为系统分析中盘子河段四大家鱼栖息地适宜度指标的变化规律,数模计算选取包括枯水流量和中水流量在内的多级流量,计算工况见表1。
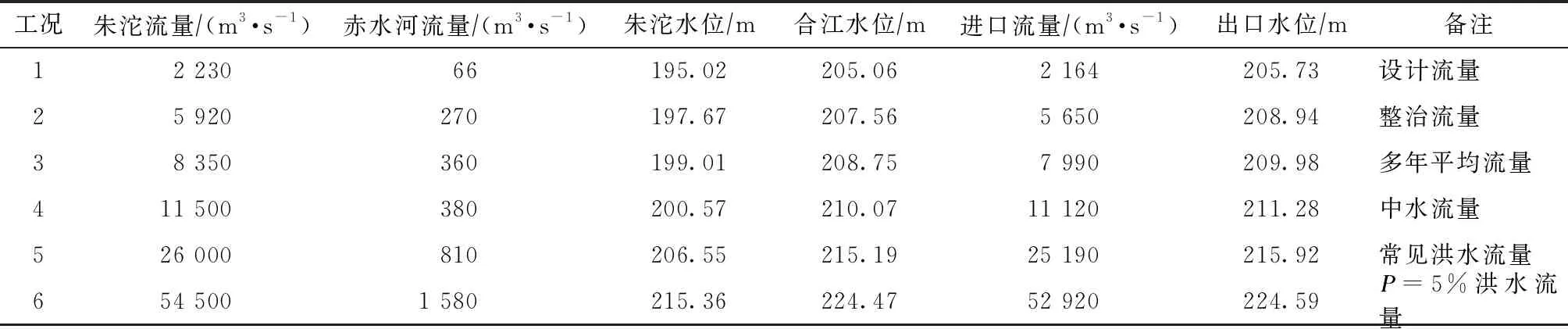
表1 数模计算工况参数
1.2 分析方法
根据现有研究,产卵栖息地适宜度可用流速适宜度SV、水深适宜度SD、栖息地适宜指数SH和微生境适应性面积SA等参数进行评价,计算公式为
SHi=SVi×SDi
(4)
(5)
式中:SVi、SDi、SHi分别表示网格节点i的流速适宜度、水深适宜度和栖息地适宜指数,SVi、SDi、SHi均为0~1之间的无量纲数值;SVi、SDi根据平面二维水流数值模拟获得的节点i流速和水深,通过四大家鱼水深和流速适宜性曲线[17]确定;SHj为第j单元中心的栖息地适宜指数,根据该单元6个节点的SHi插值计算得到;Aj表示第j单元的水表面面积;n为单元总数;SA为根据SHj加权计算得到的微生境适宜性面积。
2 适宜度指标随流量的变化特征
2.1 栖息地适宜度指数
在复杂弯道水流的作用下,河道往往会形成具有边滩和深槽的横断面形态,该断面形态在弯道出口附近尤为明显。下面以弯道出口附近(弯角65°)的典型横断面为例进行分析,图2给出该断面适宜度参数随流量的变化。结果显示:
1)枯水流量时(工况1),凹岸边滩基本不过流,流速适宜度SV总体为0,滩槽交互区的SV逐渐增大,至深槽处SV接近于1,该区域具有较适合鱼类产卵栖息的流速。流量增大后(工况2~4),深槽SV呈逐渐减小的趋势,SV最大值出现的位置逐渐由滩槽交互区向凹岸边滩转移。流量继续增大(工况5~6),河道流速明显增加,深槽SV基本为0,边滩SV沿两岸方向逐渐增大,SV较大值主要出现在河道两侧的边滩附近。
2)水深适宜度SD在边滩和深槽也呈现不同的变化规律。当流量较小时(工况1),深槽处具有较适合鱼类产卵栖息的水深,流量增大后(工况2~6),河道水位抬高,深槽水深增大,逐渐超出鱼类产卵栖息的最适宜水深,SD呈逐渐减小的趋势。边滩处SD变化趋势与深槽总体相反,SD经历了“先增大后减小”的变化过程;流量较小时(工况1),边滩水深不足,SD较小;流量增大后(工况2~5),边滩水深增加,SD相应增大;但流量增加到一定程度后(工况6),边滩水深超过鱼类产卵栖息的最适宜水深,SD将会变小。
3)栖息地适宜指数SH体现了流速适宜度SV和水深适宜度SD的综合作用。流量较小时(工况1)在深槽处SH接近1,随流量增大深槽处SH逐渐减小,边滩处SH随流量的增大呈“先增大后减小”的变化趋势;当水深较小时,适于鱼类产卵栖息的区域主要集中在深槽;流量增大后,该区域逐渐向河岸迁移。
综上所述,适于鱼类产卵栖息的区域将随流量的变化而在深槽和边滩之间进行转化,小流量下该区域多居深槽,流量增大后该区域多居边滩。总体上看,多年平均流量下(工况3),SH> 0.8的河宽最大,表明该流量下鱼类产卵栖息条件最好。
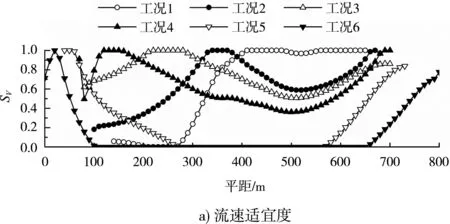
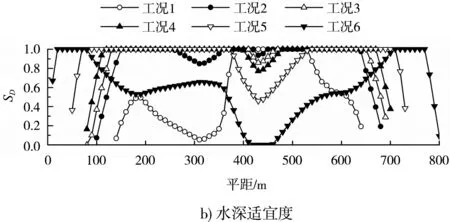
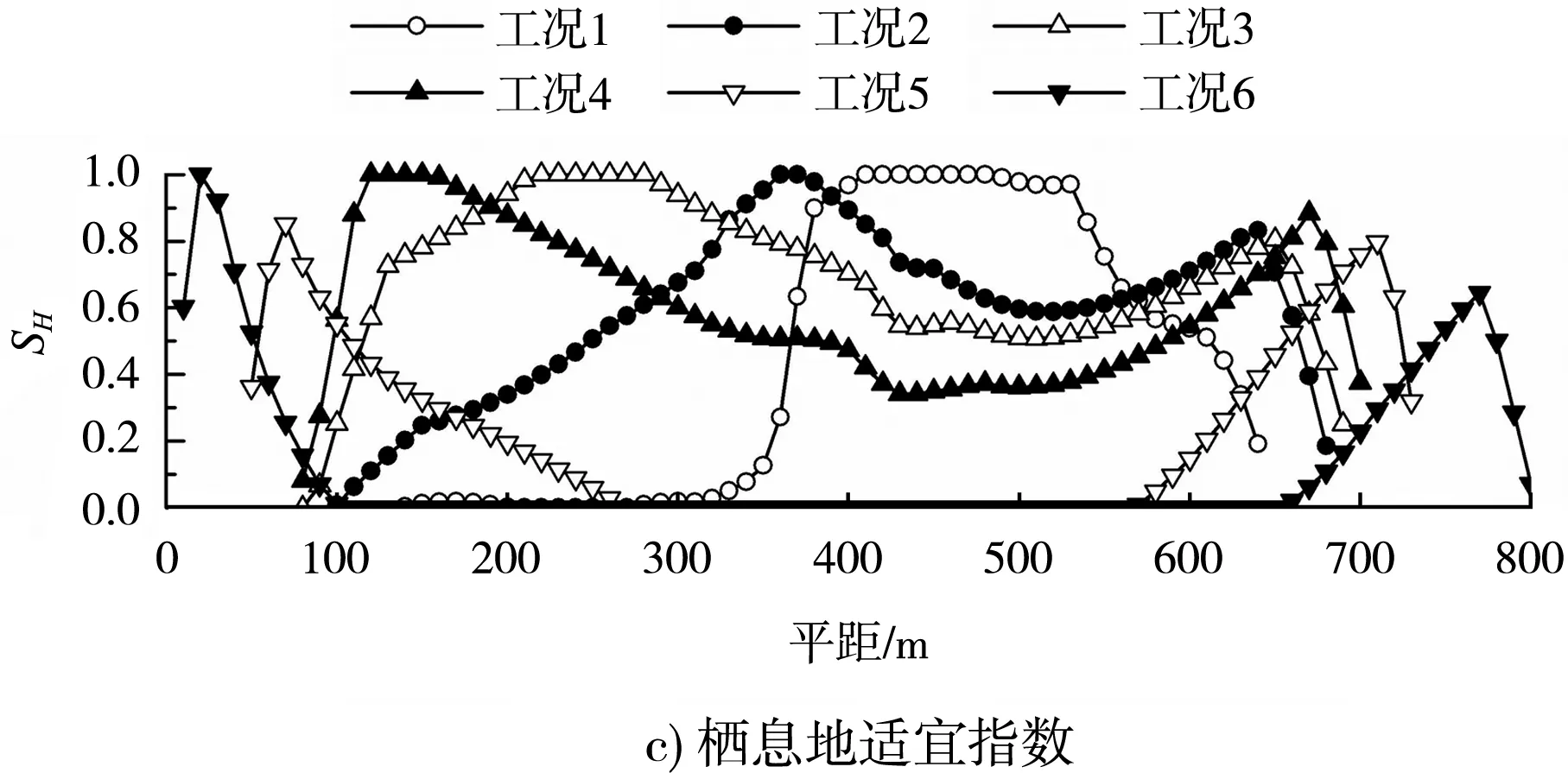
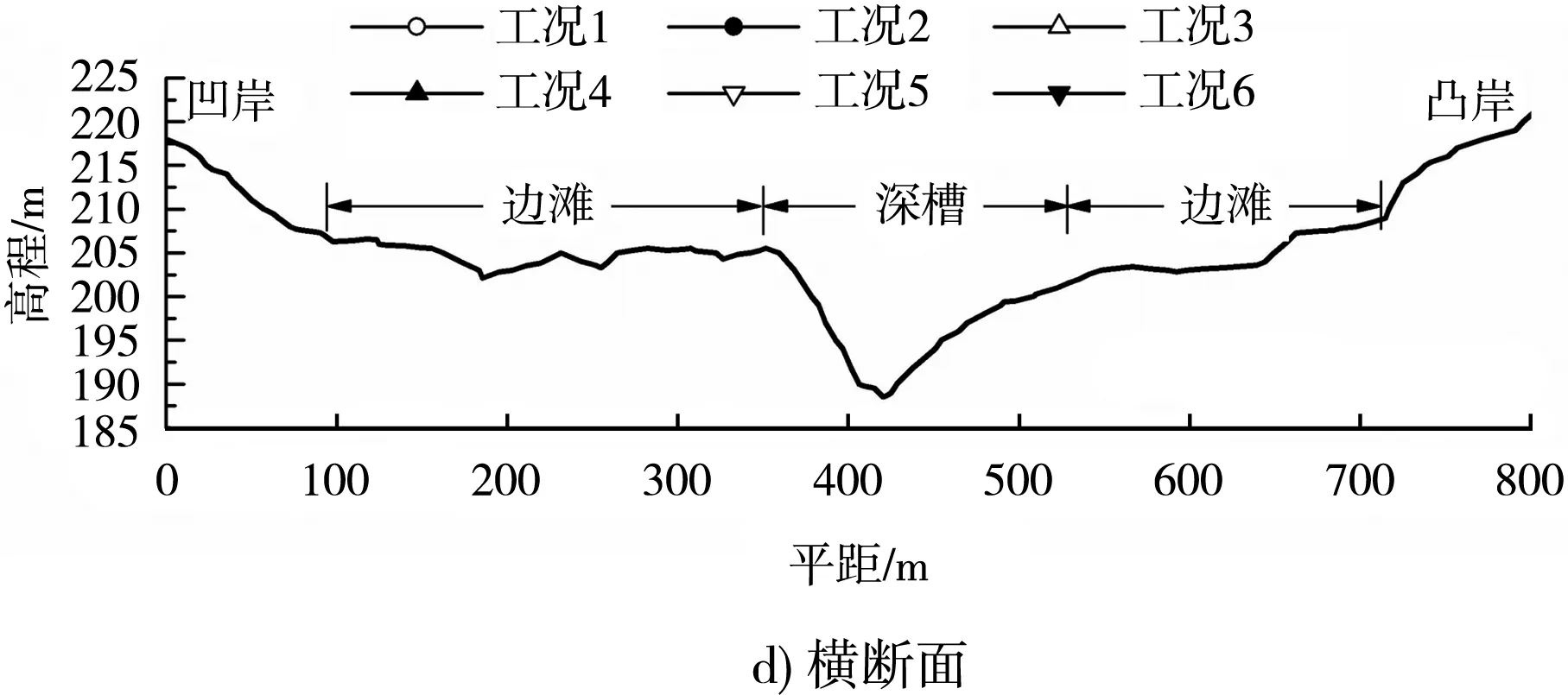
图2 适宜度参数随流量的变化
2.2 微生境适宜性面积
系用1.2节的方法计算河道区域各单元的栖息地适宜指数SH后,即可统计大于某SH值的面积AH。由于面积值与河道长度有关,统计时已将面积值转换为1 km长度的数值。图3a)给出各计算工况下大于某SH的面积AH变化。可见,AH随SH的增大而减小,递减变化趋势随流量的增大呈现“缓慢→加快→缓慢”的过程,河段流量5 650 m3/s ≤Q≤ 11 120 m3/s时(工况2~4),AH随SH总体接近线性递减变化,递减速度较其余流量时更快。图3b)进一步给出SH> 0.8所对应面积AH随流量Q的变化。结果表明,AH随流量Q呈“先增大后减小”的变化趋势,峰值出现在多年平均流量(工况3)附近,中水时期的面积最大。
根据式(5)可计算由SH加权得到的微生境适宜性面积SA。图3c)给出SA随流量Q的变化,与AH随流量Q的变化趋势相似,SA随流量Q也呈“先增大后减小”的变化特征,SA峰值出现在多年平均流量附近,中水时期微生境适宜面积最大。
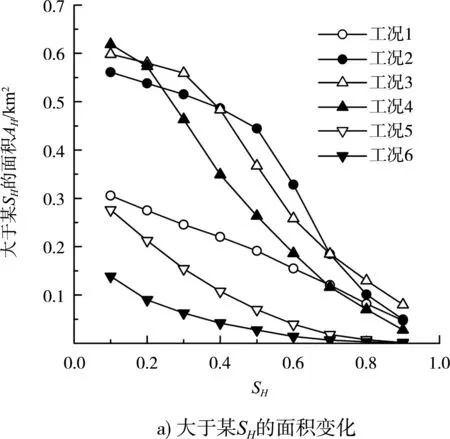
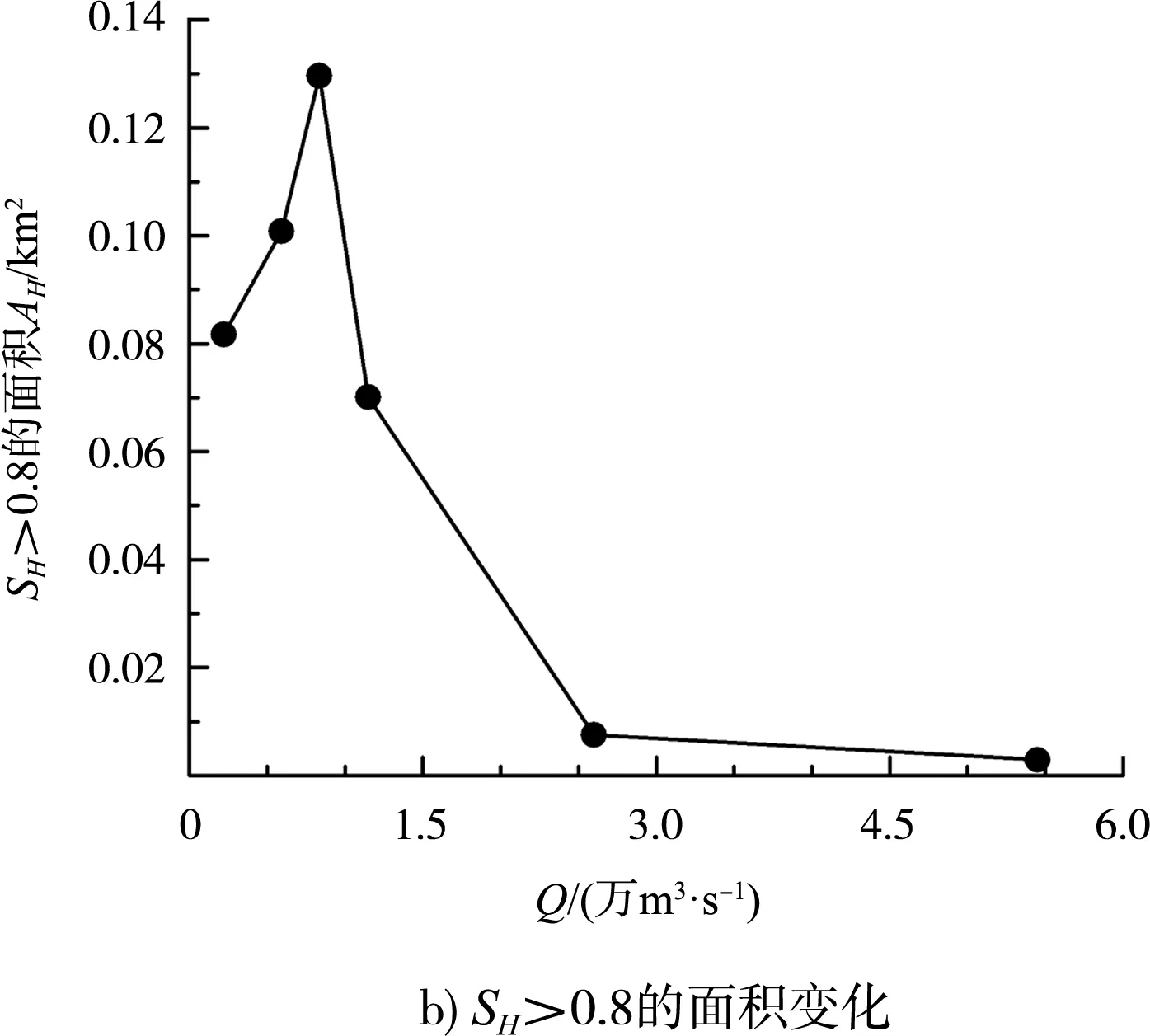
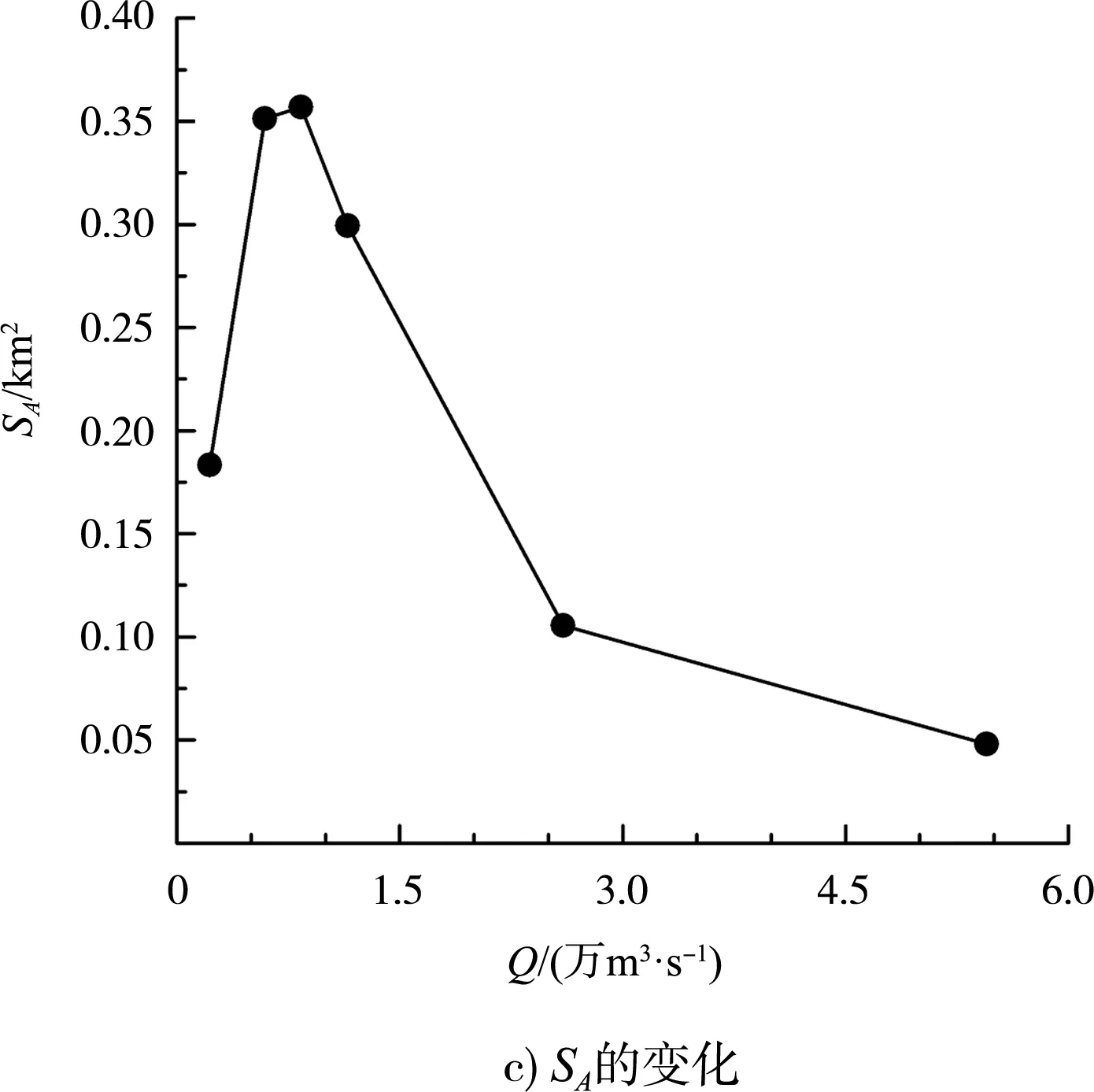
图3 微生境适宜性面积随流量的变化
3 适宜度指标在弯道中的分布规律
前述研究得出最适于鱼类产卵栖息的流量为多年平均流量(工况3)。因此,本节以多年平均流量为例,从适宜度指标的总体分布及其随弯道中心角和横向位置的变化等方面,进一步分析适宜度指标在弯道中的分布规律。
3.1 适宜度指标的总体分布
图4给出多年平均流量下的流速适宜度SV、水深适宜度SD和栖息地适宜指数SH分布云图。结果显示:1)SV值较大区域主要出现在河道两侧区域,尤其在凹岸中盘子石梁和凸岸鼓眼碛边滩附近的SV值较大,一般大于0.8,水流流速较适合鱼类产卵栖息。2)凹岸中盘子石梁和凸岸双线子、鼓眼碛边滩等处因水深较小,SD值较小,在0.4~0.6;此外,河道内其余区域的SD值接近1,鱼类产卵栖息具有较好的水深条件。3)SH的分布
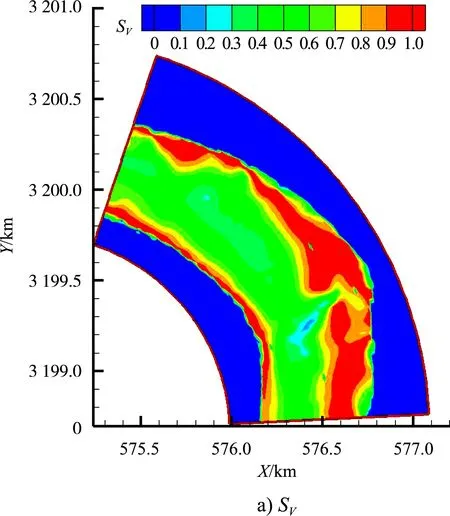
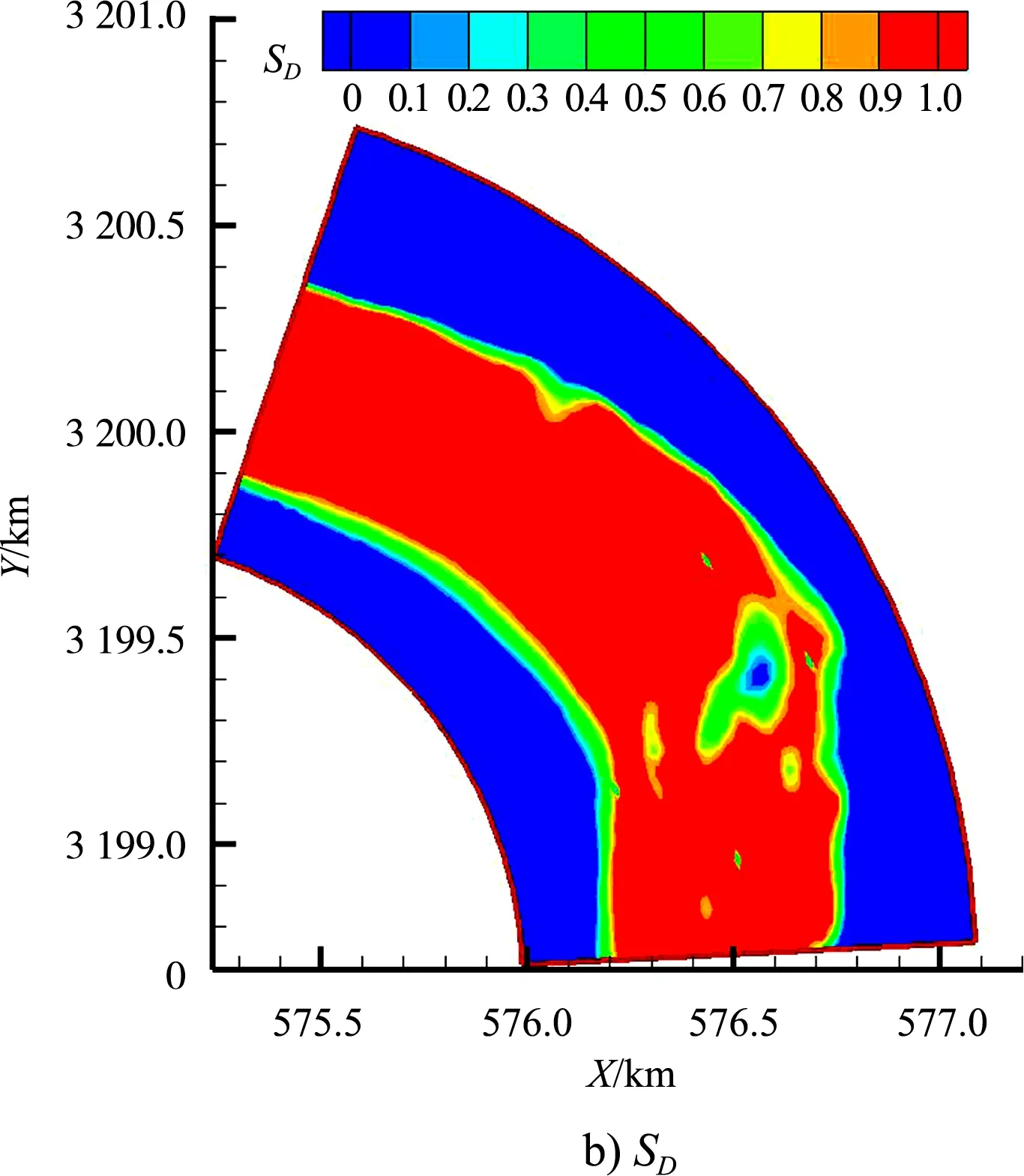
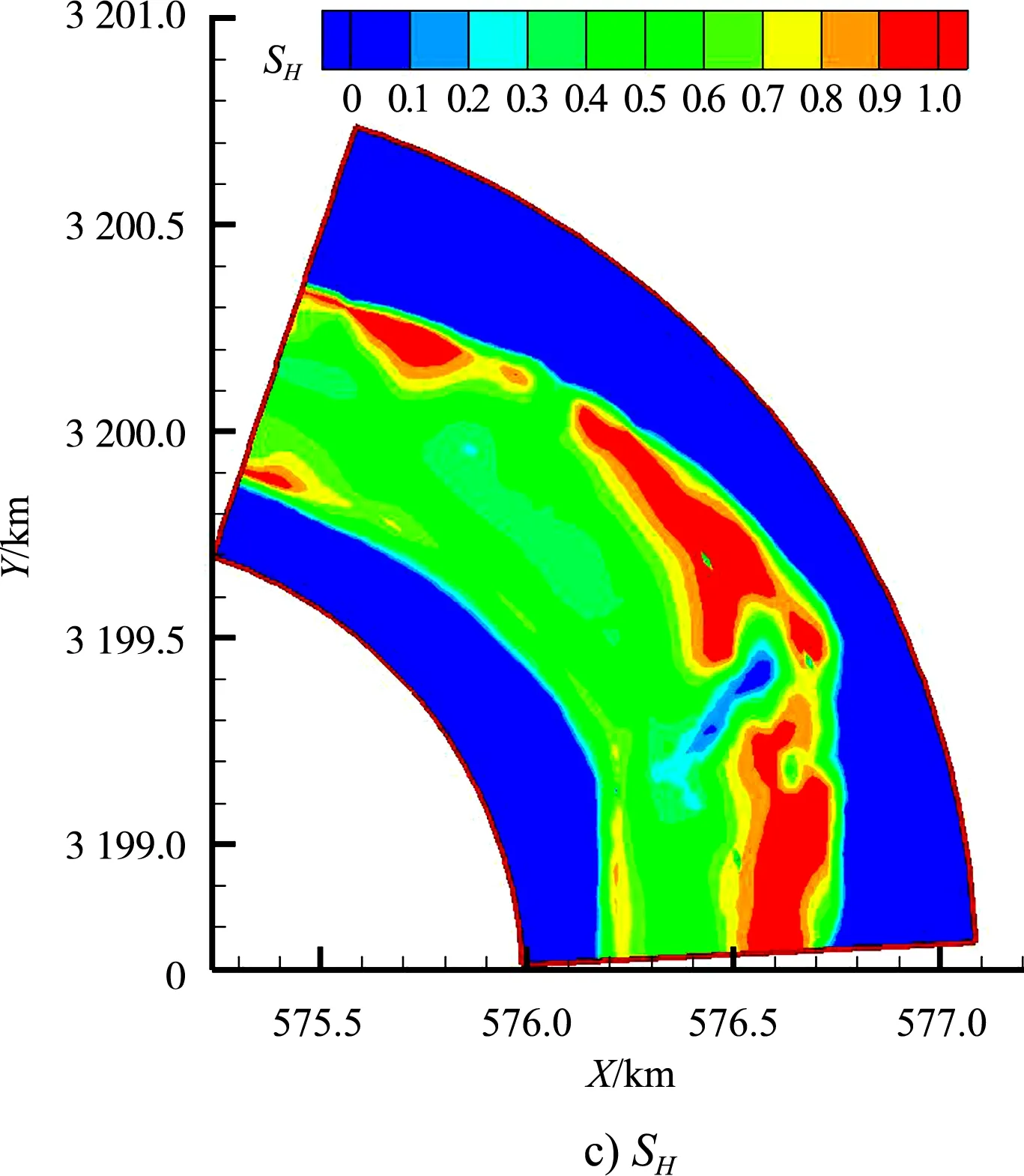
图4 适宜度参数的分布云图
与SV总体相似,较大值的出现位置也基本吻合,这是由于在多年平均流量下,河道内具有较适于鱼类产卵栖息的水深(SD值较接近1),SH主要受SV影响,因而两者分布规律具有一致性。
3.2 随弯道中心角的变化
图5给出多年平均流量下河道凹岸、深泓和凸岸3个纵剖面的适宜度参数沿程变化。分析表明:1)受石梁凸嘴等局部地形影响,凹岸剖面地形呈锯齿状,高程起伏变化复杂,流速适宜度SV、水深适宜度SD和栖息地适宜指数SH沿程分布波动明显,SV、SD和SH的平均值分别为0.668、0.204和0.133。2)河道深泓剖面的水深适宜度SD均为1,SV和SH的沿程分布重合,平均值为0.529。3)凸岸剖面地形沿程变化相对平缓,SV、SD和SH的沿程波动也较凹岸减弱,平均值分别为0.845、0.110和0.093。4)比较而言,河道两岸的SV较大,具有较适于鱼类产卵栖息的流速条件;中部深泓的SD较大,SH也明显大于两岸,鱼类产卵栖息适宜度更好。5)凹岸及凸岸的SD、SH之间均具有一定的相关性,其相关系数R2分别为0.57和0.91,SH随SD呈线性递增变化趋势。
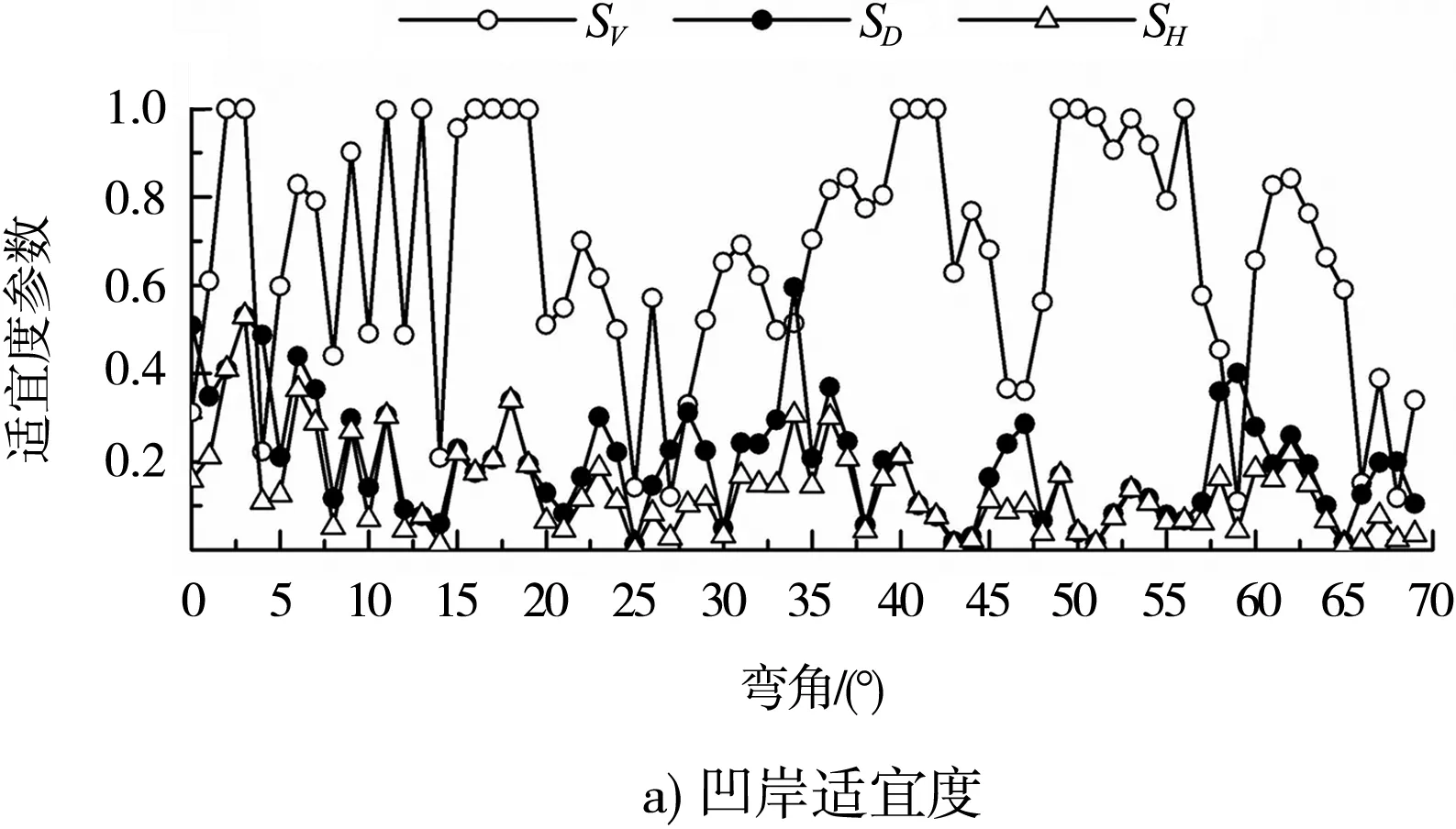
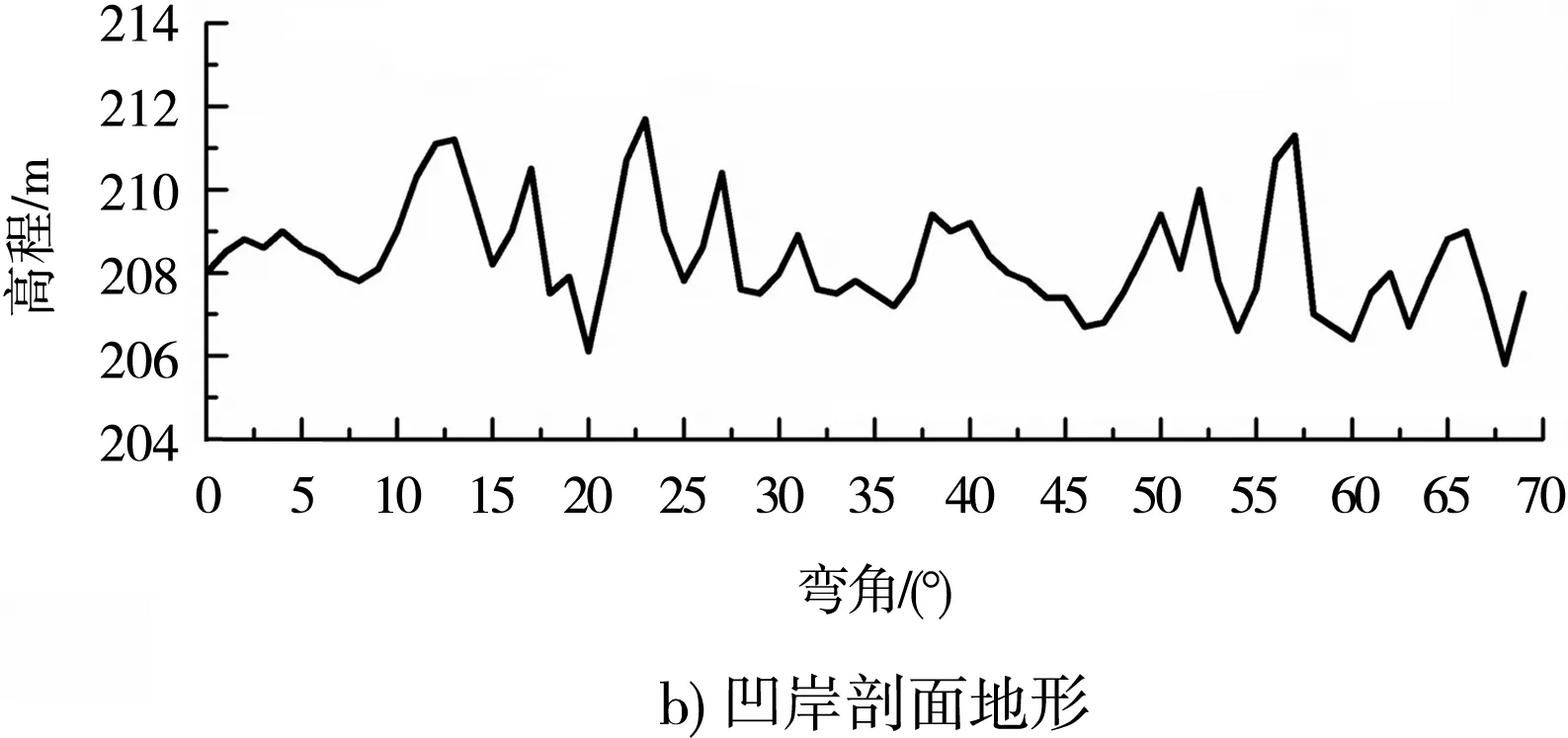
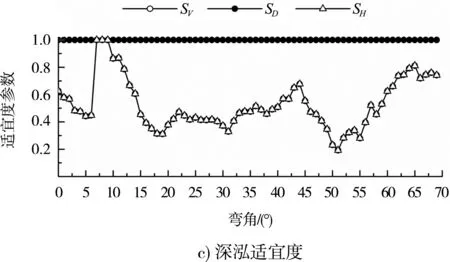
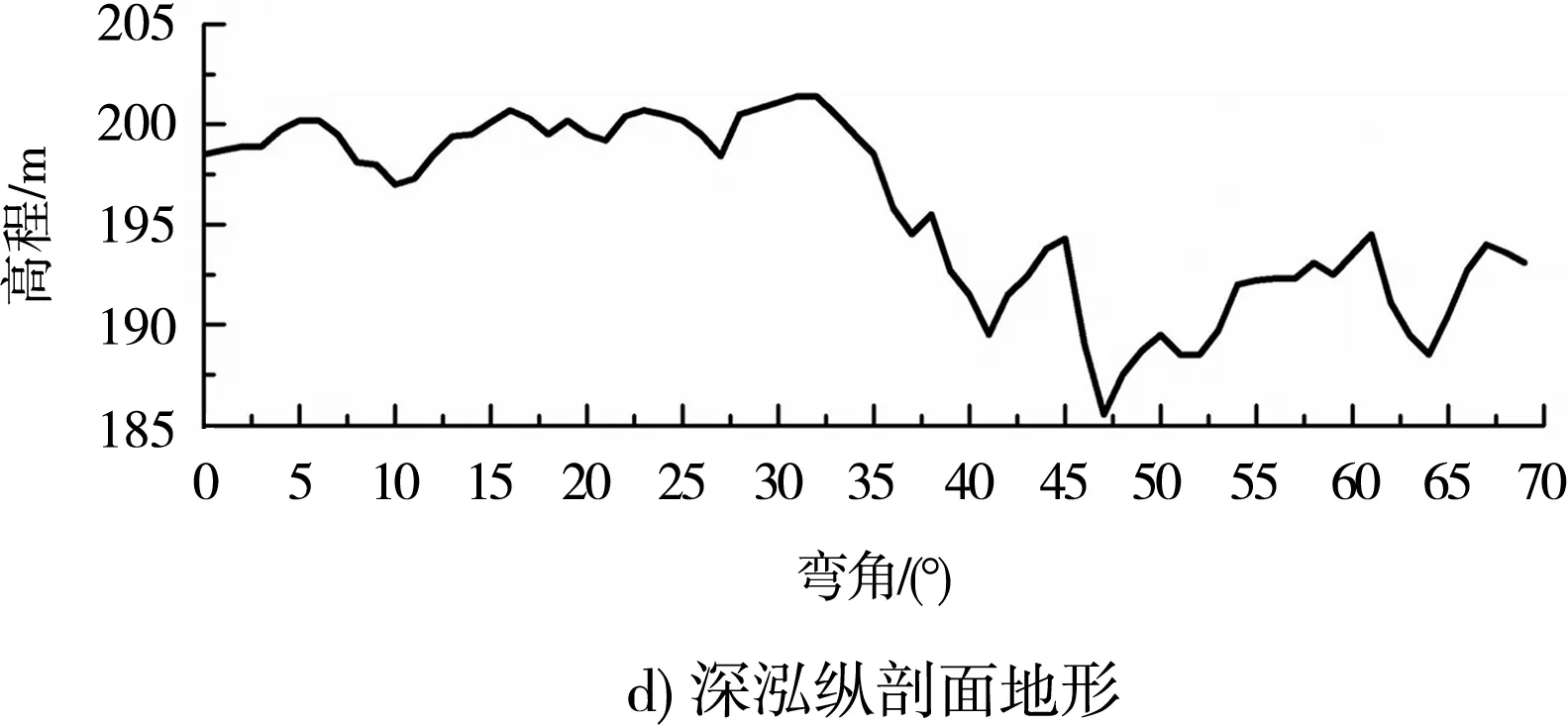
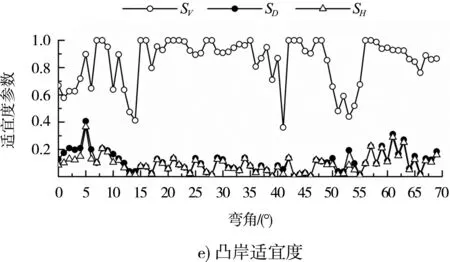

图5 适宜度参数沿程变化
3.3 随横向位置的变化
图6给出多年平均流量下弯道进口、中部和出口3个横剖面的适宜度参数沿河宽变化。结果显示:1)各断面的水深适宜度SD沿河宽分布呈“两端小、中间大”的特征,SD平均值分别为0.944、0.920和0.916,断面中部SD基本呈水平线分布,数值约为1,两岸SD骤然减小。2)SV、SH沿河宽分布总体重合,数值差异主要体现在两岸附近;弯道进口断面SV、SH的平均值分别为0.636和0.593,沿河宽呈“M”状分布,断面两岸及深泓处的SV、SH最小;中部断面SV、SH的平均值分别为0.643和0.575,沿河宽呈“S”状分布,凹岸边滩中部SV、SH最大,深槽附近SV、SH最小;出口断面SV、SH的平均值分别为0.756和0.692,沿河宽的分布形状及最大值、最小值出现位置与中部断面基本一致。3)各断面河道深泓处SH值分别为0.316、0.324和0.511,SH> 0.8的区域主要集中在河道两岸和凹岸边滩,该区域较适于鱼类产卵栖息。

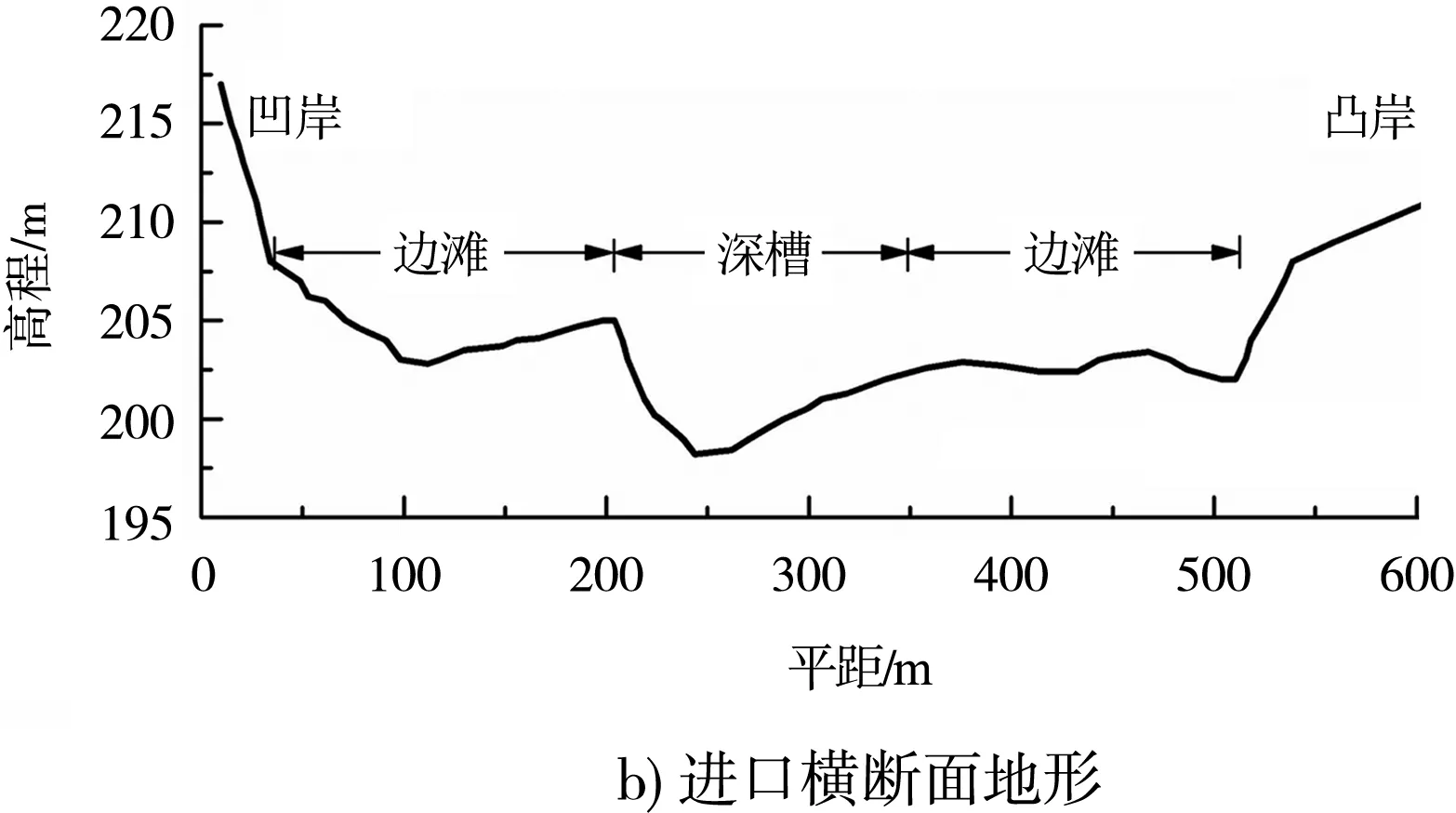

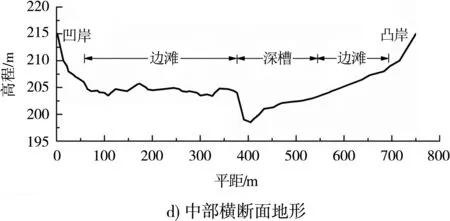
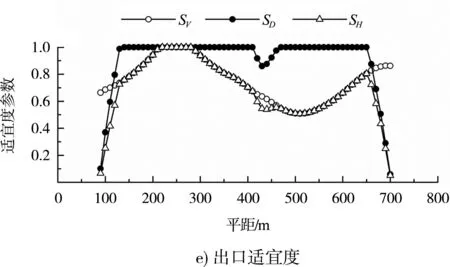
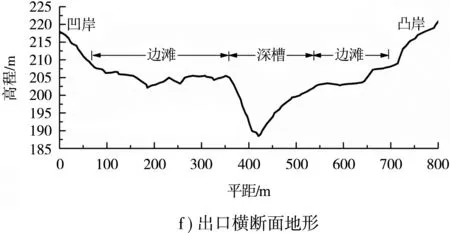
图6 适宜度参数沿河宽变化
山区弯曲河道水流运动复杂,鱼类产卵栖息适宜度研究尚处起步阶段。本文初步探讨四大家鱼产卵栖息地适宜度在弯道中的分布特征,今后可进一步研究适宜度在弯道滩槽之间的转换机制,深化对鱼类水力生境指标变化规律的认识。
4 结论
1)随着流量的变化,适于鱼类产卵栖息的区域将在深槽和边滩之间转化:小流量下适宜区域多居深槽,流量增大后适宜区域多居边滩。
2)大于某栖息地适宜指数SH的面积AH随SH的增大而减小,递减变化趋势与流量有关;微生境适宜性面积SA随流量Q呈“先增大后减小”的变化特征,SA峰值出现在多年平均流量附近。
3)河道两岸流速适宜度SV相对较大,中部深泓水深适宜度SD和栖息地适宜指数SH相对较大;凹岸及凸岸的SD、SH之间均具有一定的相关性,SH随SD呈线性递增变化趋势。
4)多年平均流量下,弯道沿程各断面的SD沿河宽分布呈“两端小、中间大”的特征,SV、SH沿河宽分布总体重合,数值差异主要体现在两岸附近;SH> 0.8的区域主要集中在河道两岸和凹岸边滩,该区域较适于鱼类产卵栖息。
